python用最小二乘法实现平面拟合
文章目录
- 数学原理
- 代码实现
- 测试
数学原理
平面方程可写为
A x + B y + C z + D = 0 Ax+By+Cz+D=0 Ax+By+Cz+D=0
假设 C C C不为0,则上式可以改写为
z = a x + b y + d z=ax+by+d z=ax+by+d
则现有一组点 { p i } \{p_i\} {pi},则根据 x i , y i x_i,y_i xi,yi以及平面方程,可以得到其对应的 z ^ i \hat z_i z^i
z ^ i = a x i + b y i + d \hat z_i=ax_i+by_i+d z^i=axi+byi+d
从而平面拟合就转换为了最小二乘问题
arg min ∑ ∣ z i − z ^ i ∣ \argmin \sum \vert z_i-\hat z_i\vert argmin∑∣zi−z^i∣
将其转换为矩阵形式,记
A = [ x 1 y 1 1 x 2 y 2 1 ⋮ ⋮ x n y n 1 ] , x = [ a b d ] , b = [ z 1 z 2 ⋮ z n ] A=\begin{bmatrix} x_1&y_1&1\\x_2&y_2&1\\\vdots&\vdots\\x_n&y_n&1 \end{bmatrix}, x=\begin{bmatrix}a\\b\\d\end{bmatrix}, b=\begin{bmatrix}z_1\\z_2\\\vdots\\z_n\end{bmatrix} A= x1x2⋮xny1y2⋮yn111 ,x= abd ,b= z1z2⋮zn
则拟合方程变为
A x = b Ax=b Ax=b
相应地 x x x可写为
x = ( A T A ) − 1 A T b x=(A^TA)^{-1}A^Tb x=(ATA)−1ATb
最小二乘法的原理可见:python实现最小二乘法
代码实现
其代码实现如下
import numpy as np
def planefit(points):xs, ys, zs = list(zip(*points))A = np.vstack([xs,ys,np.ones_like(xs)]).Tb = np.reshape(zs, [-1, 1])abd = np.linalg.inv(A.T @ A) @ A.T @ breturn abd.reshape(-1)其中输入参数points为一组点。第一步将这些点进行坐标拆分,得到一一对应的xs, ys, zs。然后通过这些点,构造矩阵A和向量b,最后输出 ( A T A ) − 1 A T b (A^TA)^{-1}A^Tb (ATA)−1ATb。
测试
首先做一个初始化平面的函数,其功能是随机生成一组在平面中的点,并且为其添加一些噪声。
# 初始化平面
def initPlane(a, b, d, N, err=0.1):xs,ys = np.random.rand(2, N)zs = a*xs + b*ys + d + np.random.rand(N)*errreturn list(zip(xs, ys, zs))
然后用planefit函数对这些点进行拟合,通过对比二者之间的差异,来证实算法的有效性
import matplotlib.pyplot as pltpts = initPlane(2,3,4,100,1)
a,b,d = planefit(pts)xs, ys = np.indices([100,100])/100
zs = a*xs + b*ys + dax = plt.subplot(projection='3d')
ax.plot_surface(xs, ys, zs, cmap='jet')
ax.scatter(*np.array(pts).T, marker='*')
plt.show()

随着加入的噪声逐渐变大,拟合误差也越来越大
errs = [0.01, 0.1, 0.2, 0.5, 1, 3, 5]
fits = []
for err in errs:pts = initPlane(2,3,4,100,1)a,b,d = planefit(pts)fits.append([abs(a-2),abs(b-3),abs(d-4)])import pprint
pprint.pprint(fits)
[[0.09377971025135245, 0.023025216275622373, 0.4933931906466551],
[0.044310965250572654, 0.05681830483294226, 0.47952260969370997],
[0.051813469166934745, 0.017914573861143257, 0.47553046120193176],
[0.08578595894551588, 0.0464898508775029, 0.42791269232718054],
[0.011569662177250528, 0.15976404558136714, 0.4886516489062753],
[0.006829071411009302, 0.04832062421804073, 0.5193494695593301],
[0.1651263679674586, 0.0736367910618192, 0.44103226768552073]]
相关文章:

python用最小二乘法实现平面拟合
文章目录 数学原理代码实现测试 数学原理 平面方程可写为 A x B y C z D 0 AxByCzD0 AxByCzD0 假设 C C C不为0,则上式可以改写为 z a x b y d zaxbyd zaxbyd 则现有一组点 { p i } \{p_i\} {pi},则根据 x i , y i x_i,y_i xi,yi以及平面…...
SpringCloud微服务:Nacos和Eureka的区别
目录 配置: 区别: ephemeral设置为true时 ephemeral设置为false时(这里我使用的服务是order-service) 1. Nacos与eureka的共同点 都支持服务注册和服务拉取 都支持服务提供者心跳方式做健康检测 2. Nacos与Eu…...

基于Springboot+Vue的校园在线打印预约系统
基于SpringbootVue的校园在线打印预约系统的设计与实现 (1) 注册功能:允许学生、教职员工注册账户,并提供安全的身份验证机制,确保只有授权用户可以使用系统。 (2) 登录功能:店家或学生可以使用各自账号登录。登录后允许修改用户…...

计算机毕业设计选题推荐-掌心办公微信小程序/安卓APP-项目实战
✨作者主页:IT毕设梦工厂✨ 个人简介:曾从事计算机专业培训教学,擅长Java、Python、微信小程序、Golang、安卓Android等项目实战。接项目定制开发、代码讲解、答辩教学、文档编写、降重等。 ☑文末获取源码☑ 精彩专栏推荐⬇⬇⬇ Java项目 Py…...

1.1二分查找
二分查找,主要是针对基本有序的数据来进行查找target。 二分法的思想很简单,因为整个数组是有序的,数组默认是递增的。 1.1 使用条件 用于查找的内容逻辑上来说是需要有序的查找的数量只能是一个,而不是多个 1.2 简介 首先选…...

提升工作效率,打造精细思维——OmniOutliner 5 Pro for Mac
在当今快节奏的工作环境中,如何高效地组织和管理我们的思维和任务成为了关键。而OmniOutliner 5 Pro for Mac正是为此而生的一款强大工具。无论你是专业写作者、项目经理还是学生,OmniOutliner 5 Pro for Mac都能帮助你提升工作效率,打造精细…...
idea显示pom.xml文件漂黄警告 Dependency maven:xxx:xxx is vulnerable
场景: idea警告某些maven依赖包有漏洞或者依赖传递有易受攻击包,如下: 解决: 1、打开idea设置,找到 File | Settings | Editor | Inspections 2、取消上述两项勾选即可...

Linux中安装部署环境(JAVA)
目录 在Linux中安装jdk 包管理器yum安装jdk JDK安装过程中的问题 验证安装jdk 在Linux中安装tomcat 安装mysql 在Linux中安装jdk jdk在Linux中的安装方式有很多种, 这里介绍最简单的方法, 也就是包管理器方法: 包管理器yum安装jdk Linux中常见的包管理器有: yumaptp…...
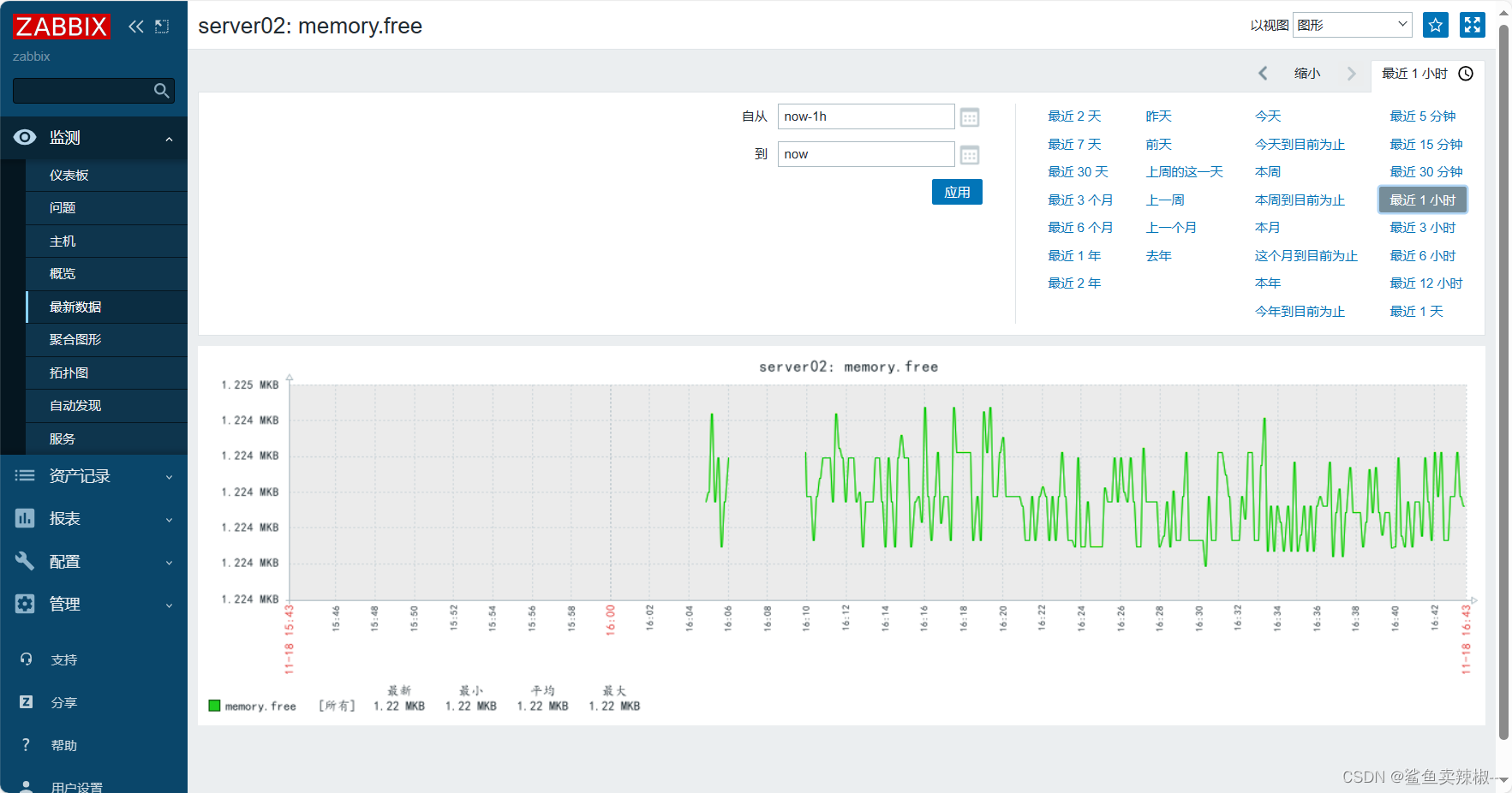
Zabbix Proxy分布式监控
目录 Zabbix Proxy简介 实验环境 proxy端配置 1.安装仓库 2.安装zabbix-proxy 3.创建初始数据库 4.导入初始架构和数据,系统将提示您输入新创建的密码 5.编辑配置文件 /etc/zabbix/zabbix_proxy.conf,配置完成后要重启。 agent客户端配置 zabbix…...

前端设计模式之【代理模式】
文章目录 前言介绍例子场景优缺点标题五后言 前言 hello world欢迎来到前端的新世界 😜当前文章系列专栏:前端设计模式 🐱👓博主在前端领域还有很多知识和技术需要掌握,正在不断努力填补技术短板。(如果出现错误&…...

Canal+Kafka实现MySQL与Redis数据同步(二)
CanalKafka实现MySQL与Redis数据同步(二) 创建MQ消费者进行同步 在application.yml配置文件加上kafka的配置信息: spring:kafka:# Kafka服务地址bootstrap-servers: 127.0.0.1:9092consumer:# 指定一个默认的组名group-id: consumer-group…...

NOIP2023模拟19联测40 诡异键盘
题目大意 有一个键盘,上面有 n 1 n1 n1个按键,按下按键 1 ≤ i ≤ n 1\leq i\leq n 1≤i≤n会打印出字符串 S i S_i Si,按下按键 n 1 n1 n1会删掉结尾的 K K K个字符,如果不足 K K K个字符则全部删完,问打印出 S …...
)
算法设计与分析 | 众数问题(c语言)
题目 所谓众数,就是对于给定的含有N个元素的多重集合,每个元素在S中出现次数最多的成为该元素的重数, 多重集合S重的重数最大的元素成为众数。例如:S{1,2,2,2,3,5},则多重集S的众数是2,其重数为3。 现在你…...

sql server外键设置
SQL Server外键设置 简介 在关系型数据库中,外键是一种约束,用于确保数据的完整性和一致性。外键约束定义了一个表中的列与另一个表中的列之间的关系,它可以用来保证数据的一致性、防止数据的破坏和数据冗余。在SQL Server中,我们…...
)
R语言实现多变量孟德尔随机化分析(1)
多变量孟德尔随机化分析调整了潜在混杂因素的影响。 1、调整哪些因素?参考以往文献。可以分别调整,也可以一起调整。 2、解决了什么问题?某个暴露相关的SNP,往往与某个或者某几个混杂因素相关。可以控制混杂偏倚。 3、如何解释…...
搭建 AI 图像生成器 (SAAS) php laravel
今天来搭一套,AI 图像生成器 是基于 Openai DALLE 2 和 Openai DALLE 3 以及 Stability AI 和稳定扩散 API 构建的脚本,为用户提供了使用简单的提示和大小生成独特自定义图像的可能性。在这个平台上,创意得以快速、高效地实现,借助…...

Maven引用本地jar包
先上命令: mvn install:install-file -Dfile..\.m2\repository\jl1.0.1.jar -DgroupId"com.liz.local" -DartifactId"jl" -Dversion"1.0.1" -Dpackagingjar 参数注释: -Dfile: jar 包路径(建议放在 meven 的 repository&…...

一起学docker系列之五docker的常用命令--操作容器的命令
目录 前言1 启动容器2 查看容器3 退出容器4 启动已经停止的容器5 重启容器6 停止容器7 删除已经停止的容器8 启动容器说明和举例9 查看容器日志10 查看容器内运行的进程11 查看容器内部细节12 进入正在运行的容器并进行交互13 导入和导出容器结语 前言 当涉及到容器化技术&…...

WPF打开对话框选择文件、选择文件夹
在WPF中实现文件的打开和选择,可以通过使用Microsoft.Win32.OpenFileDialog类来完成。这是一个通用的对话框组件,允许用户在本地文件系统中浏览和选择文件。这个组件属于WPF的一部分,因此不需要引用额外的库。 以下是一个如何使用OpenFileDi…...

nginx学习(3)
Nginx 负载均衡 实战案例 实现效果 浏览器地址栏输入地址 http://172.31.0.99/oa/a.html,负载均衡效果,平均 8083 和 8084 端口中 一、配置 1、先创建2个文件夹,并将apache-tomcat-8.5.87解压到tomcat8083和tomcat8084中 (或…...

测试微信模版消息推送
进入“开发接口管理”--“公众平台测试账号”,无需申请公众账号、可在测试账号中体验并测试微信公众平台所有高级接口。 获取access_token: 自定义模版消息: 关注测试号:扫二维码关注测试号。 发送模版消息: import requests da…...

安宝特方案丨XRSOP人员作业标准化管理平台:AR智慧点检验收套件
在选煤厂、化工厂、钢铁厂等过程生产型企业,其生产设备的运行效率和非计划停机对工业制造效益有较大影响。 随着企业自动化和智能化建设的推进,需提前预防假检、错检、漏检,推动智慧生产运维系统数据的流动和现场赋能应用。同时,…...

linux 错误码总结
1,错误码的概念与作用 在Linux系统中,错误码是系统调用或库函数在执行失败时返回的特定数值,用于指示具体的错误类型。这些错误码通过全局变量errno来存储和传递,errno由操作系统维护,保存最近一次发生的错误信息。值得注意的是,errno的值在每次系统调用或函数调用失败时…...

【AI学习】三、AI算法中的向量
在人工智能(AI)算法中,向量(Vector)是一种将现实世界中的数据(如图像、文本、音频等)转化为计算机可处理的数值型特征表示的工具。它是连接人类认知(如语义、视觉特征)与…...

以光量子为例,详解量子获取方式
光量子技术获取量子比特可在室温下进行。该方式有望通过与名为硅光子学(silicon photonics)的光波导(optical waveguide)芯片制造技术和光纤等光通信技术相结合来实现量子计算机。量子力学中,光既是波又是粒子。光子本…...

08. C#入门系列【类的基本概念】:开启编程世界的奇妙冒险
C#入门系列【类的基本概念】:开启编程世界的奇妙冒险 嘿,各位编程小白探险家!欢迎来到 C# 的奇幻大陆!今天咱们要深入探索这片大陆上至关重要的 “建筑”—— 类!别害怕,跟着我,保准让你轻松搞…...

uniapp 开发ios, xcode 提交app store connect 和 testflight内测
uniapp 中配置 配置manifest 文档:manifest.json 应用配置 | uni-app官网 hbuilderx中本地打包 下载IOS最新SDK 开发环境 | uni小程序SDK hbulderx 版本号:4.66 对应的sdk版本 4.66 两者必须一致 本地打包的资源导入到SDK 导入资源 | uni小程序SDK …...

C# 表达式和运算符(求值顺序)
求值顺序 表达式可以由许多嵌套的子表达式构成。子表达式的求值顺序可以使表达式的最终值发生 变化。 例如,已知表达式3*52,依照子表达式的求值顺序,有两种可能的结果,如图9-3所示。 如果乘法先执行,结果是17。如果5…...

【深度学习新浪潮】什么是credit assignment problem?
Credit Assignment Problem(信用分配问题) 是机器学习,尤其是强化学习(RL)中的核心挑战之一,指的是如何将最终的奖励或惩罚准确地分配给导致该结果的各个中间动作或决策。在序列决策任务中,智能体执行一系列动作后获得一个最终奖励,但每个动作对最终结果的贡献程度往往…...

Unity VR/MR开发-VR开发与传统3D开发的差异
视频讲解链接:【XR马斯维】VR/MR开发与传统3D开发的差异【UnityVR/MR开发教程--入门】_哔哩哔哩_bilibili...
