NOIP2023模拟19联测40 诡异键盘
题目大意
有一个键盘,上面有 n + 1 n+1 n+1个按键,按下按键 1 ≤ i ≤ n 1\leq i\leq n 1≤i≤n会打印出字符串 S i S_i Si,按下按键 n + 1 n+1 n+1会删掉结尾的 K K K个字符,如果不足 K K K个字符则全部删完,问打印出 S S S最少要按多少次。
有 T T T组数据。
1 ≤ T ≤ 100 , 10 ≤ n ≤ 5 × 1 0 3 , 1 ≤ ∑ K ≤ 2 × 1 0 3 1\leq T\leq 100,10\leq n\leq 5\times 10^3,1\leq \sum K\leq 2\times 10^3 1≤T≤100,10≤n≤5×103,1≤∑K≤2×103
1 ≤ ∑ ( ∑ ∣ S i ∣ ) ≤ 1 0 6 , 1 ≤ ∑ ∣ S ∣ ≤ 5 × 1 0 3 1\leq \sum(\sum|S_i|)\leq 10^6,1\leq \sum |S|\leq 5\times 10^3 1≤∑(∑∣Si∣)≤106,1≤∑∣S∣≤5×103
时间限制 2000 m s 2000ms 2000ms,空间限制 512 M B 512MB 512MB。
题解
考虑 D P DP DP,设 f i f_i fi表示打出前 i i i个字符需要的最小操作次数。那我们要求的就是打出 S S S的第 i i i个字符到第 j j j个字符需要的最小操作次数。
先考虑如何得到 S S S中 [ i , j ] [i,j] [i,j]这一段。我们选择一个前 j − i + 1 j-i+1 j−i+1个字符与 S S S的 [ i , j ] [i,j] [i,j]中的字符相同的 S p S_p Sp,然后将 S p S_p Sp打出并删到只剩下 S S S的 [ i , j ] [i,j] [i,j]这部分即可。我们可以建一棵字典树,每次加入一个 S i S_i Si时更新从根节点到达路径上每个点的最小操作次数。为了求这里的最小操作次数,我们还需要求出删除若干个字符所需要的最小操作次数,这个可以用一个类似“同余”的最短路来求出,用 dijkstra \text{dijkstra} dijkstra可以 O ( K 2 ) O(K^2) O(K2)解决(连边是 O ( k 2 ) O(k^2) O(k2)的,求最短路是 O ( K log K ) O(K\log K) O(KlogK)的)。
得到了带到每个位置的最小操作次数之后,枚举每个 i i i,然后在字典树上按 S S S从 i i i往后枚举,设枚举到 j j j,则用 f i f_i fi来更新 f j f_j fj。 D P DP DP的时间复杂度为 O ( ∣ S ∣ 2 ) O(|S|^2) O(∣S∣2)。
总时间复杂度为 O ( ∑ ( ∑ ∣ S i ∣ + ∣ S ∣ 2 + K 2 ) ) O(\sum(\sum |S_i|+|S|^2+K^2)) O(∑(∑∣Si∣+∣S∣2+K2))。
可以参考代码帮助理解。
code
#include<bits/stdc++.h>
using namespace std;
const int N=5000,M=1000000,K=2000;
int T,n,k,s1,now,bg[N+5],len[N+5],z[K+5],vs[K+5],cm[K+5];
int tot;
char s[N+5],t[M+5],ss[M+5];
long long dis[K+5],to[M+5],f[N+5];
struct node{int x;long long dis;bool operator<(const node ax)const{return dis>ax.dis;}
};
vector<pair<int,int>>g[K+5];
priority_queue<node>q;
struct trie{int a[26];
}w[M+5];
void pt(){int len=strlen(ss+1);for(int i=1;i<=len;i++){t[++now]=ss[i];}
}
void init(){for(int i=0;i<k;i++){z[i]=1e9;vs[i]=cm[i]=0;g[i].clear();}for(int i=1;i<=n;i++){len[i]=bg[i+1]-bg[i];z[len[i]%k]=min(z[len[i]%k],len[i]);vs[len[i]%k]=1;}for(int i=1;i<=n;i++){if(z[len[i]%k]!=len[i]) continue;if(!vs[len[i]%k]) continue;vs[len[i]%k]=0;for(int j=0;j<k;j++){g[(j+len[i])%k].push_back({j,1+(j+len[i])/k});}}for(int i=0;i<k;i++) dis[i]=1e16;dis[0]=dis[k]=0;q.push((node){0,0});while(!q.empty()){int u=q.top().x;q.pop();if(cm[u]) continue;cm[u]=1;for(auto p:g[u]){int v=p.first,w=p.second;if(dis[u]+w<dis[v]){dis[v]=dis[u]+w;q.push((node){v,dis[v]});}}}
}
void pt(int tw){int q,vq=1;for(int i=1;i<=len[tw];i++){q=t[bg[tw]+i-1]-'a';if(!w[vq].a[q]){w[vq].a[q]=++tot;to[tot]=1e16;}vq=w[vq].a[q];to[vq]=min(to[vq],1ll+(len[tw]-i)/k+dis[(len[tw]-i)%k]);}
}
void solve(int tw){int q,vq=1;for(int i=tw+1;i<=s1;i++){q=s[i]-'a';if(!w[vq].a[q]) return;vq=w[vq].a[q];f[i]=min(f[i],f[tw]+to[vq]);}
}
int main()
{
// freopen("keyboard.in","r",stdin);
// freopen("keyboard.out","w",stdout);scanf("%d",&T);while(T--){scanf("%d%d",&n,&k);now=0;for(int i=1;i<=n;i++){scanf("%s",ss+1);bg[i]=now+1;pt();}bg[n+1]=now+1;scanf("%s",s+1);s1=strlen(s+1);init();tot=1;for(int i=1;i<=n;i++) pt(i);for(int i=0;i<=s1;i++) f[i]=1e16;f[0]=0;for(int i=0;i<s1;i++) solve(i);if(f[s1]>=1e16) printf("-1\n");else printf("%lld\n",f[s1]);for(int i=1;i<=tot;i++){for(int j=0;j<26;j++) w[i].a[j]=0;}}return 0;
}
相关文章:

NOIP2023模拟19联测40 诡异键盘
题目大意 有一个键盘,上面有 n 1 n1 n1个按键,按下按键 1 ≤ i ≤ n 1\leq i\leq n 1≤i≤n会打印出字符串 S i S_i Si,按下按键 n 1 n1 n1会删掉结尾的 K K K个字符,如果不足 K K K个字符则全部删完,问打印出 S …...
)
算法设计与分析 | 众数问题(c语言)
题目 所谓众数,就是对于给定的含有N个元素的多重集合,每个元素在S中出现次数最多的成为该元素的重数, 多重集合S重的重数最大的元素成为众数。例如:S{1,2,2,2,3,5},则多重集S的众数是2,其重数为3。 现在你…...

sql server外键设置
SQL Server外键设置 简介 在关系型数据库中,外键是一种约束,用于确保数据的完整性和一致性。外键约束定义了一个表中的列与另一个表中的列之间的关系,它可以用来保证数据的一致性、防止数据的破坏和数据冗余。在SQL Server中,我们…...
)
R语言实现多变量孟德尔随机化分析(1)
多变量孟德尔随机化分析调整了潜在混杂因素的影响。 1、调整哪些因素?参考以往文献。可以分别调整,也可以一起调整。 2、解决了什么问题?某个暴露相关的SNP,往往与某个或者某几个混杂因素相关。可以控制混杂偏倚。 3、如何解释…...
搭建 AI 图像生成器 (SAAS) php laravel
今天来搭一套,AI 图像生成器 是基于 Openai DALLE 2 和 Openai DALLE 3 以及 Stability AI 和稳定扩散 API 构建的脚本,为用户提供了使用简单的提示和大小生成独特自定义图像的可能性。在这个平台上,创意得以快速、高效地实现,借助…...

Maven引用本地jar包
先上命令: mvn install:install-file -Dfile..\.m2\repository\jl1.0.1.jar -DgroupId"com.liz.local" -DartifactId"jl" -Dversion"1.0.1" -Dpackagingjar 参数注释: -Dfile: jar 包路径(建议放在 meven 的 repository&…...

一起学docker系列之五docker的常用命令--操作容器的命令
目录 前言1 启动容器2 查看容器3 退出容器4 启动已经停止的容器5 重启容器6 停止容器7 删除已经停止的容器8 启动容器说明和举例9 查看容器日志10 查看容器内运行的进程11 查看容器内部细节12 进入正在运行的容器并进行交互13 导入和导出容器结语 前言 当涉及到容器化技术&…...

WPF打开对话框选择文件、选择文件夹
在WPF中实现文件的打开和选择,可以通过使用Microsoft.Win32.OpenFileDialog类来完成。这是一个通用的对话框组件,允许用户在本地文件系统中浏览和选择文件。这个组件属于WPF的一部分,因此不需要引用额外的库。 以下是一个如何使用OpenFileDi…...

nginx学习(3)
Nginx 负载均衡 实战案例 实现效果 浏览器地址栏输入地址 http://172.31.0.99/oa/a.html,负载均衡效果,平均 8083 和 8084 端口中 一、配置 1、先创建2个文件夹,并将apache-tomcat-8.5.87解压到tomcat8083和tomcat8084中 (或…...

【系统架构设计】计算机公共基础知识: 4 数据库系统
目录 一 数据库模式 二 分布式数据库 三 索引和视图 四 数据库设计 五 关系代数...
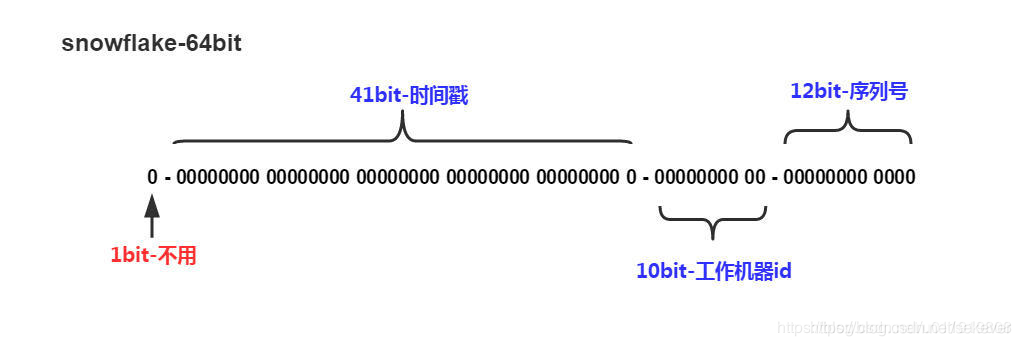
主键问题以及分布式 id
分布式 id 需要处理的问题主要是同一时间在多台机器中保证生成的 id 唯一,为了这么做我们可以这么做: 分布式 id 生成策略 先说几个已经被淘汰的策略引出分布式 id 的问题 1,UUID:UUID 随机并且唯一,在单一的数据库…...

ReentranReadWriteLock 使用案例
ReentranReadWriteLock使用案例 /*** ReentranReadWriteLock 使用案例* 读线程共享* 写线程互斥*/ public class ReentrantReadWriteLockExample {private String news;private ReentrantReadWriteLock lock new ReentrantReadWriteLock();public String readNews() {lock.re…...

“我们把最扎心的话,说给了自己最亲近的人” 何解?| IDCF
引子 我们把最好的一面给了陌生人,却把最扎心的话,说给了自己最亲近的人。 我们往往会对关心自己的人发脾气,很多时候意图是好的,表达方式却简单粗暴,结果自然不必多言。你认为自己给的是反馈和建议,对方…...

MongoDB之索引和聚合
文章目录 一、索引1、说明2、原理3、相关操作3.1、创建索引3.2、查看集合索引3.3、查看集合索引大小3.4、删除集合所有索引(不包含_id索引)3.5、删除集合指定索引 4、复合索引 二、聚合1、说明2、使用 总结 一、索引 1、说明 索引通常能够极大的提高查…...

【GEE】基于GEE进行非监督学习
1 简介与摘要 之前写了多季节叠加的监督学习,所以这次简单写一个非监督学习吧。。 这次为了简单明了,就不整那么多虚的了,在这里我不叠图层了,有需要的可以参考前一篇博客自己添加输入的图层。 2 制作输入影像 首先,…...

多视图聚类的论文阅读(一)
当聚类的方式使用的是某一类预定义好的相似性度量时, 会出现如下情况: 数据聚类方面取得了成功,但它们通常依赖于预定义的相似性度量,而这些度量受原始方法的影响:当输入维数相对较高时,往往是无效的。 1. Deep Mult…...

K-Means算法进行分类
已知数据集D中有9个数据点,分别是(1,2),(2,3), (2,1), (3,1),(2,4),(3,5),(4,3),(1,5),(4,2)。采用K-Means算法进行聚类,k2,设初始中心点为(1.1,2.2),(2.3,3.…...

深度学习交通车辆流量分析 - 目标检测与跟踪 - python opencv 计算机竞赛
文章目录 0 前言1 课题背景2 实现效果3 DeepSORT车辆跟踪3.1 Deep SORT多目标跟踪算法3.2 算法流程 4 YOLOV5算法4.1 网络架构图4.2 输入端4.3 基准网络4.4 Neck网络4.5 Head输出层 5 最后 0 前言 🔥 优质竞赛项目系列,今天要分享的是 🚩 *…...
网络协议入门 笔记一
一、服务器和客户端及java的概念 JVM (Java Virtual Machine) : Java虚拟机,Java的跨平台:一次编译,到处运行,编译生成跟平台无关的字节码文件 (class文件),由对应平台的JVM解析字节码为机器指令 (010101)。 如下图所示࿰…...
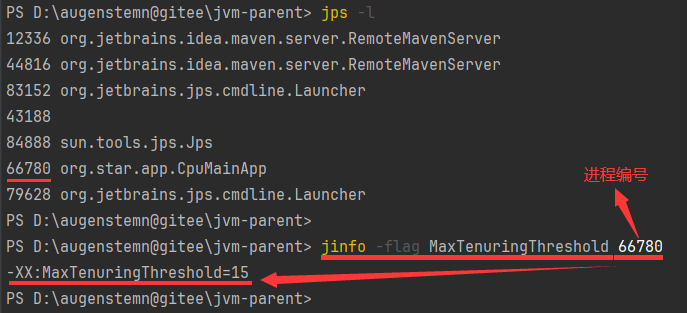
系列十一、你平时工作用过的JVM常用基本配置参数有哪些?
一、常用参数 1.1、-Xms 功能:初始内存大小,默认为物理内存的1/64,等价于 -XX:InitialHeapSize 1.2、-Xmx 功能:最大分配内存,默认为物理内存的1/4,等价于 -XX:MaxHeapSize 1.3、-Xss 功能:设置…...

Unity3D中Gfx.WaitForPresent优化方案
前言 在Unity中,Gfx.WaitForPresent占用CPU过高通常表示主线程在等待GPU完成渲染(即CPU被阻塞),这表明存在GPU瓶颈或垂直同步/帧率设置问题。以下是系统的优化方案: 对惹,这里有一个游戏开发交流小组&…...
)
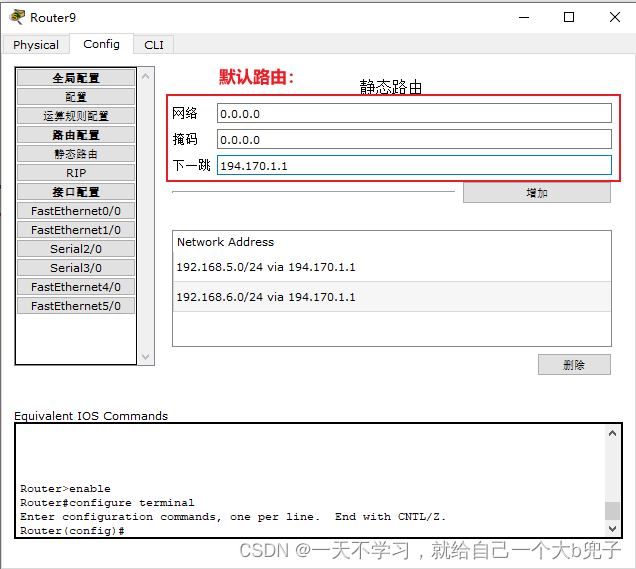
IGP(Interior Gateway Protocol,内部网关协议)
IGP(Interior Gateway Protocol,内部网关协议) 是一种用于在一个自治系统(AS)内部传递路由信息的路由协议,主要用于在一个组织或机构的内部网络中决定数据包的最佳路径。与用于自治系统之间通信的 EGP&…...

深入理解JavaScript设计模式之单例模式
目录 什么是单例模式为什么需要单例模式常见应用场景包括 单例模式实现透明单例模式实现不透明单例模式用代理实现单例模式javaScript中的单例模式使用命名空间使用闭包封装私有变量 惰性单例通用的惰性单例 结语 什么是单例模式 单例模式(Singleton Pattern&#…...

html css js网页制作成品——HTML+CSS榴莲商城网页设计(4页)附源码
目录 一、👨🎓网站题目 二、✍️网站描述 三、📚网站介绍 四、🌐网站效果 五、🪓 代码实现 🧱HTML 六、🥇 如何让学习不再盲目 七、🎁更多干货 一、👨…...

虚拟电厂发展三大趋势:市场化、技术主导、车网互联
市场化:从政策驱动到多元盈利 政策全面赋能 2025年4月,国家发改委、能源局发布《关于加快推进虚拟电厂发展的指导意见》,首次明确虚拟电厂为“独立市场主体”,提出硬性目标:2027年全国调节能力≥2000万千瓦࿰…...

nnUNet V2修改网络——暴力替换网络为UNet++
更换前,要用nnUNet V2跑通所用数据集,证明nnUNet V2、数据集、运行环境等没有问题 阅读nnU-Net V2 的 U-Net结构,初步了解要修改的网络,知己知彼,修改起来才能游刃有余。 U-Net存在两个局限,一是网络的最佳深度因应用场景而异,这取决于任务的难度和可用于训练的标注数…...

xmind转换为markdown
文章目录 解锁思维导图新姿势:将XMind转为结构化Markdown 一、认识Xmind结构二、核心转换流程详解1.解压XMind文件(ZIP处理)2.解析JSON数据结构3:递归转换树形结构4:Markdown层级生成逻辑 三、完整代码 解锁思维导图新…...

Java设计模式:责任链模式
一、什么是责任链模式? 责任链模式(Chain of Responsibility Pattern) 是一种 行为型设计模式,它通过将请求沿着一条处理链传递,直到某个对象处理它为止。这种模式的核心思想是 解耦请求的发送者和接收者,…...

STL 2迭代器
文章目录 1.迭代器2.输入迭代器3.输出迭代器1.插入迭代器 4.前向迭代器5.双向迭代器6.随机访问迭代器7.不同容器返回的迭代器类型1.输入 / 输出迭代器2.前向迭代器3.双向迭代器4.随机访问迭代器5.特殊迭代器适配器6.为什么 unordered_set 只提供前向迭代器? 1.迭代器…...
无头浏览器技术:Python爬虫如何精准模拟搜索点击
1. 无头浏览器技术概述 1.1 什么是无头浏览器? 无头浏览器是一种没有图形用户界面(GUI)的浏览器,它通过程序控制浏览器内核(如Chromium、Firefox)执行页面加载、JavaScript渲染、表单提交等操作。由于不渲…...
