斯坦福机器学习 Lecture2 (假设函数、参数、样本等等术语,还有批量梯度下降法、随机梯度下降法 SGD 以及它们的相关推导,还有正态方程)
假设函数定义
假设函数,猜一个 x->y 的类型,比如 y = ax + b,随后监督学习的任务就是找到误差最低的 a 和 b 参数
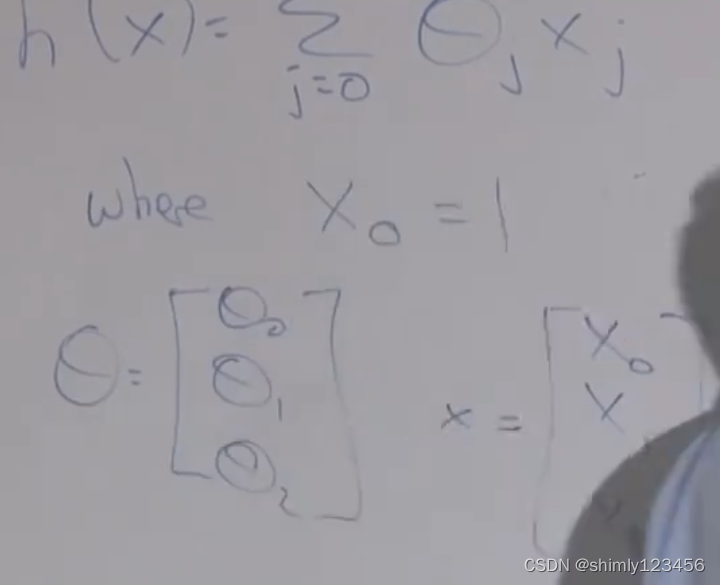
有时候我们可以定义 x0 = 1,来让假设函数的整个表达式一致统一

如上图是机器学习中的一些术语
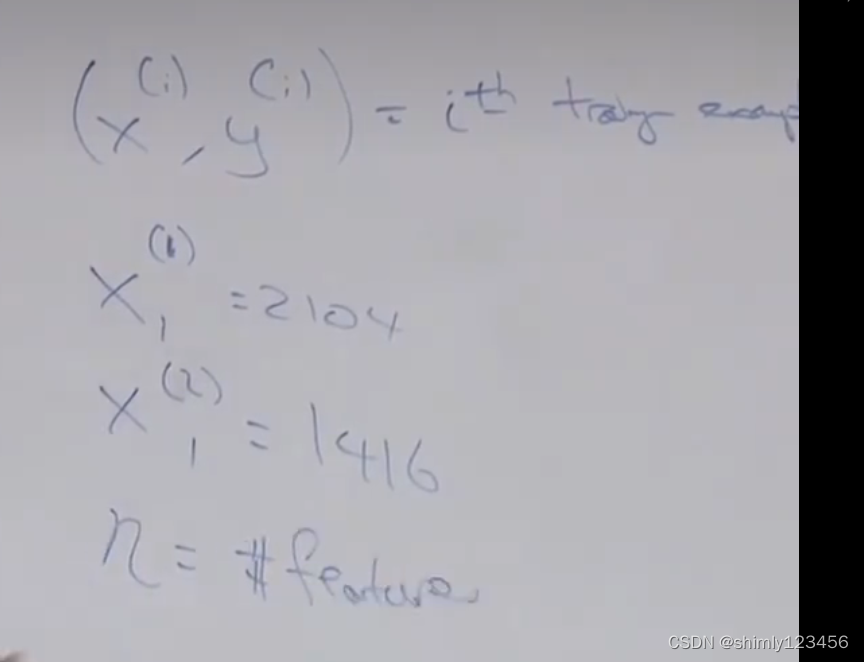
额外的符号,使用 (xi, yi) 表示第 i 个样本
n 表示特征数量 (在房屋价格预测问题中,属性/特征有两个:房子面积和卧室数量,因此这里 n = 2)
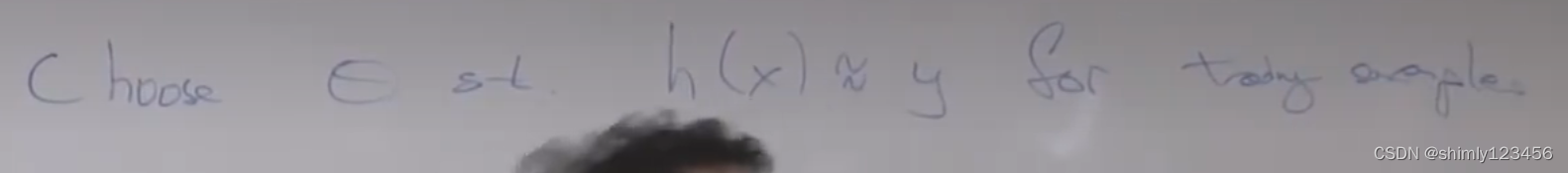
监督学习的过程就是选择合适的参数,来让假设函数的输出和样本输出相近(针对训练集)
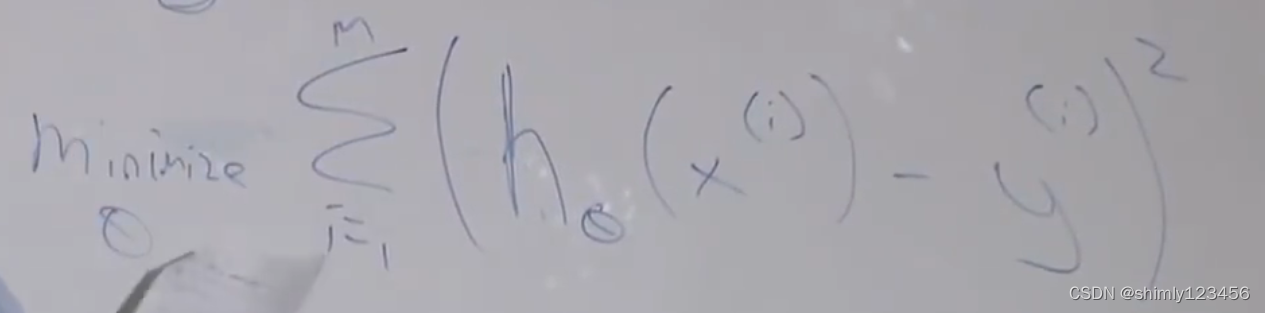
房屋预测案例中的目标函数,最小化误差平方和

我们通常会在目标函数旁边放个 1/2,这是为了后边简化求导计算
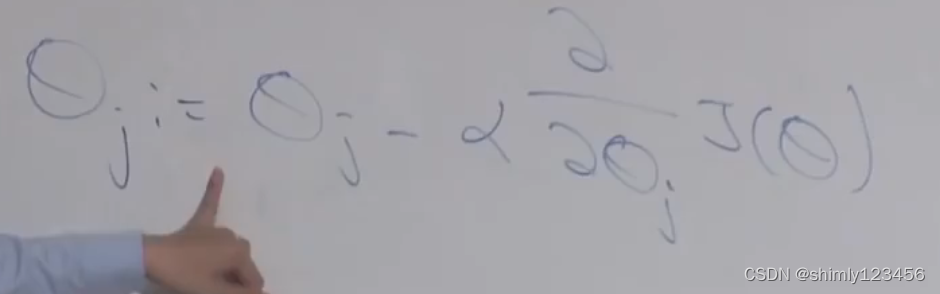
我们通常使用梯度下降法来选取更加合适的 theta参数 来优化目标函数,如上图是梯度下降法中的 “baby step”
这里的 阿尔法 就是学习速率
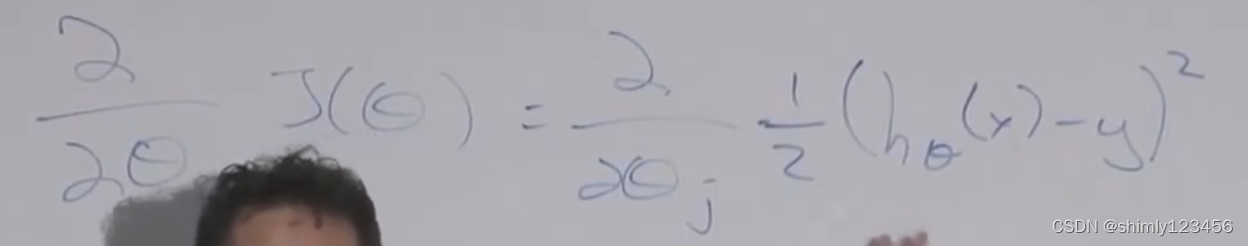
如图,是对目标函数的求导 (由于对几个项的和求导,等于它们的导数和,所以这里我们先不 care 那个 sum(sigma) 符号)
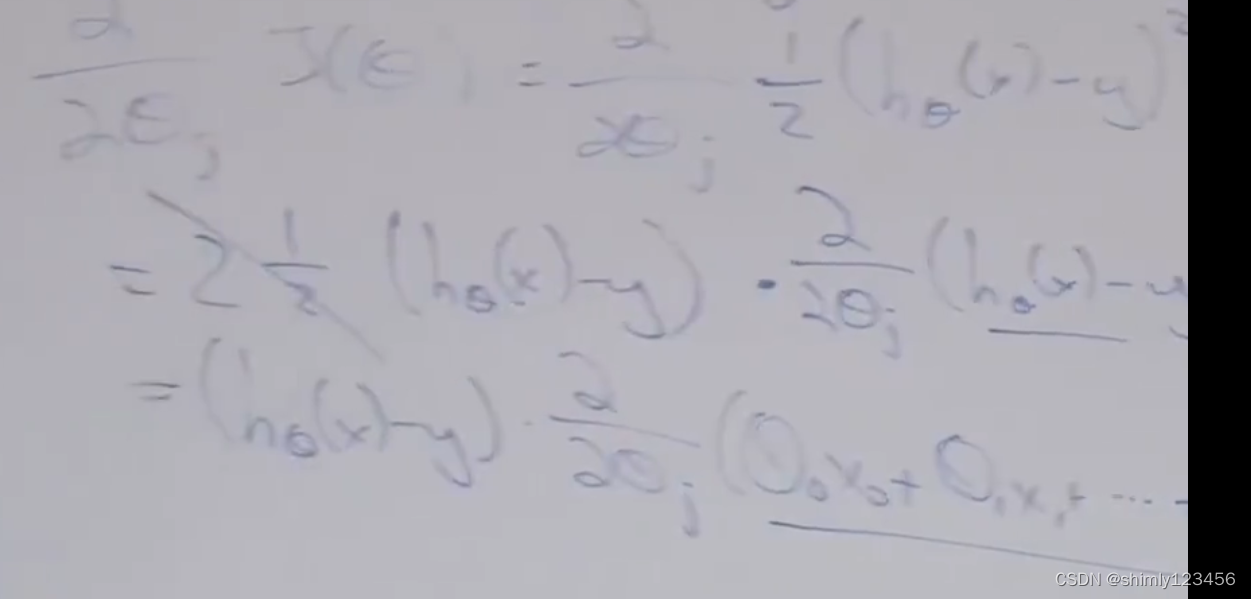
如图,是对求导公式的后续转换

如图,这是对目标函数求导的最终公式的其中一项 (这里只对 theta_j 求导)
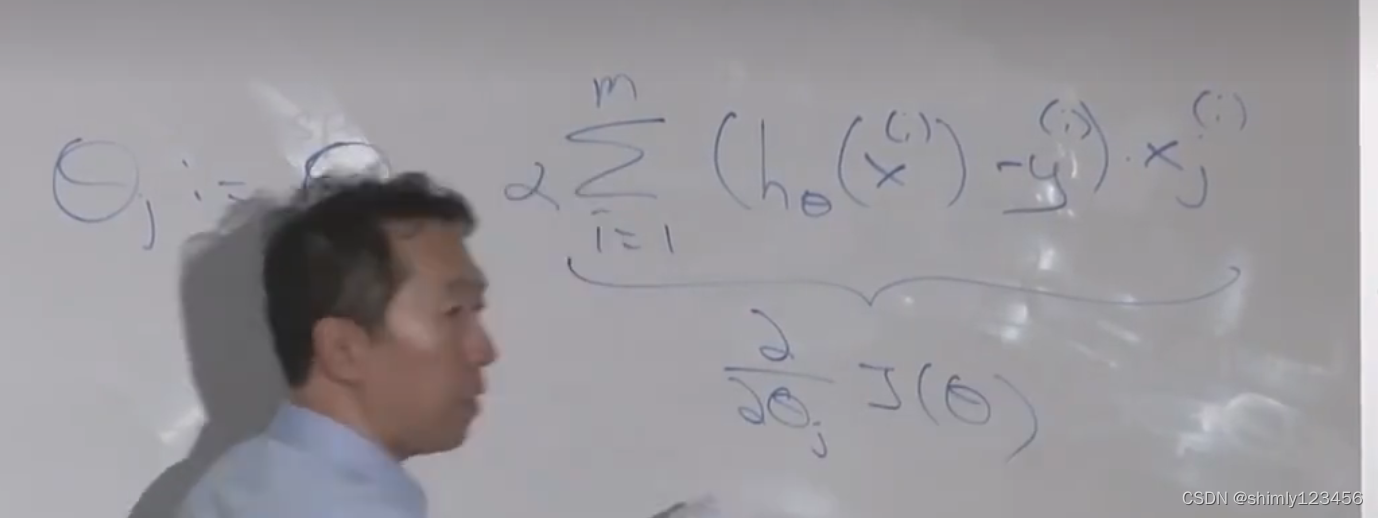
这也是最后统合得到的求导公式,对每一个样本 i 进行针对 theta_j 的求导
接下来要做的就是,重复 updating theta_j,直到目标函数收敛

由于我们的目标函数对于每个 theta_j 都是二次函数,所以这是一个凸函数,它是一个大碗,它只有一个全局最优
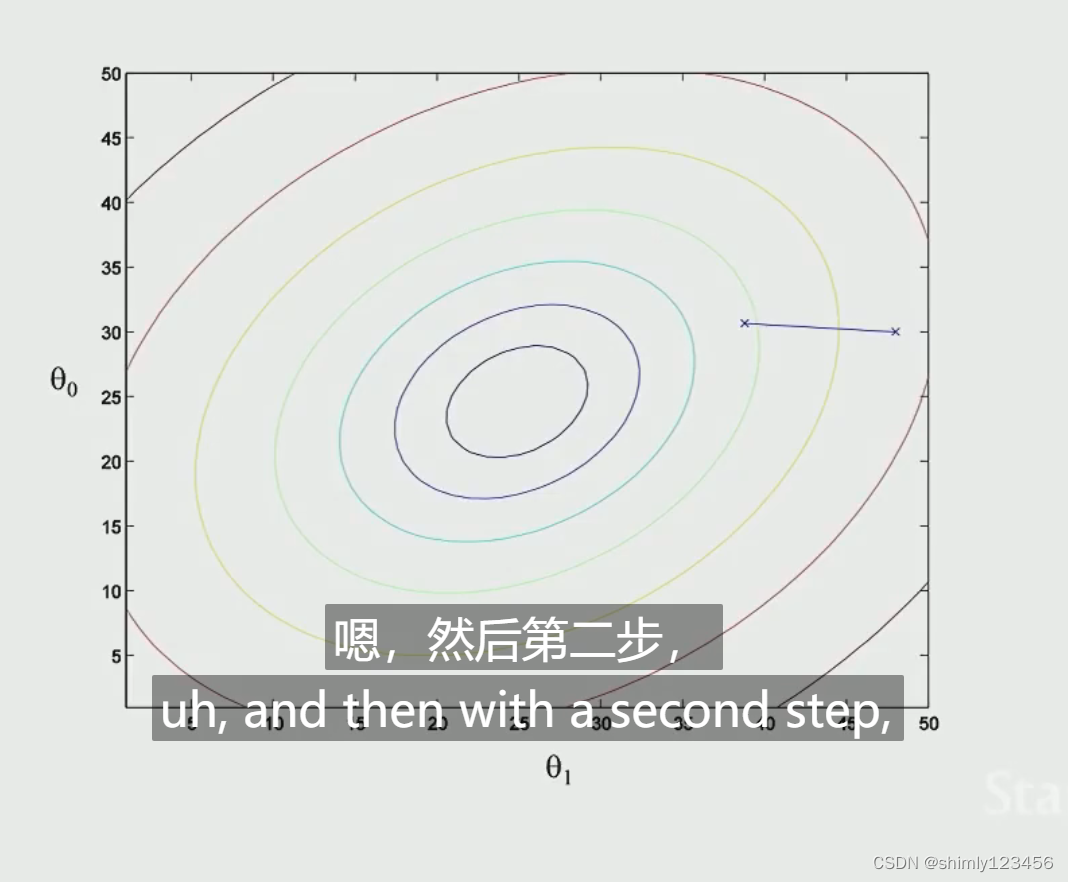
也可以用等高线图来表示
运用高中的一些数学知识,你会发现,最陡的防线和等高线(椭圆)的切线是90度
调试学习率的一些经验:
如果你发现目标函数在增加而不是减少,那通常说明学习率太大了(超调)
可以尝试 O1, O2, O4, O8 尝试不同的值
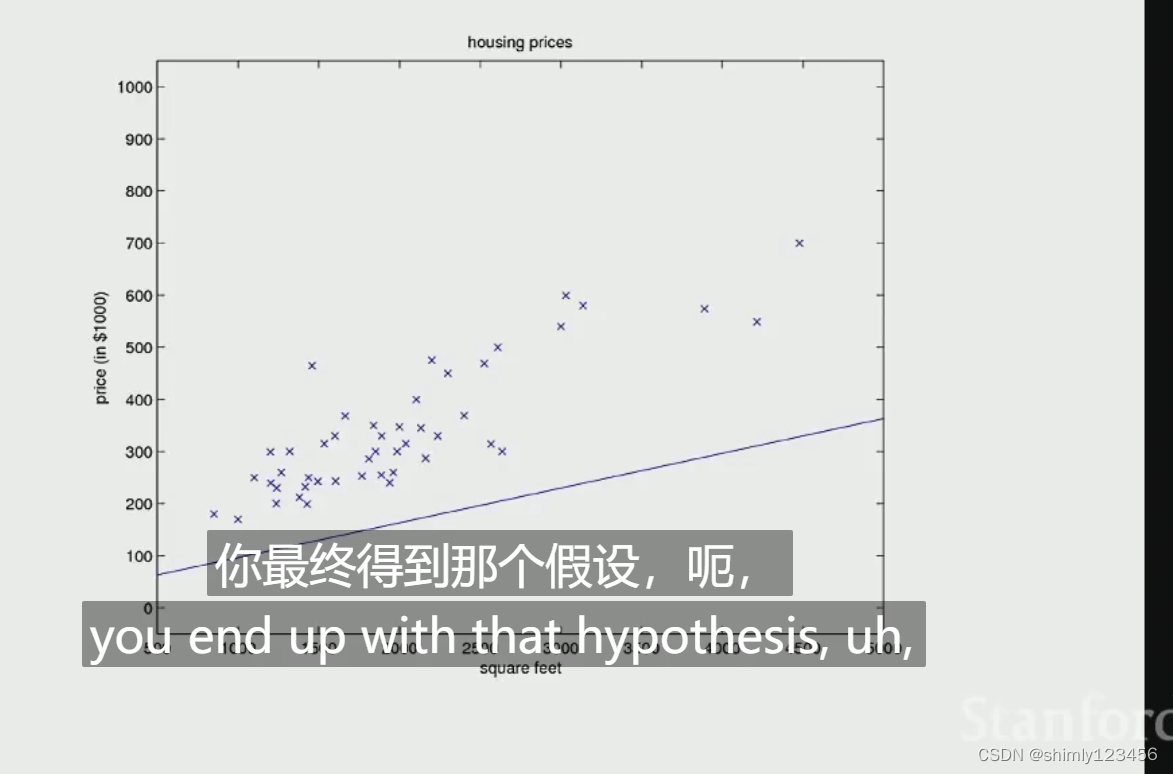
另一种可视化学习过程的方式是,看到曲线(假设函数)一点点变化
刚刚提到的机器学习方法中,梯度下降需要用到训练集中所有的样本,来计算梯度(所以也叫批量梯度下降法)。在训练集很大的情况下,这会变得昂贵,因此我们需要做些改变

另一种快得多的方式是随机梯度下降法,它遍历每一个样本 i,随后针对这单个样本对所有的 theta_j 做梯度下降
(原先的方法中,我们每做一个 tiny step 都需要扫描一次所有的样本;而 SGD 中,我们每走一个 step 只需要扫描一个样本,因此快得多)
一个更直观的解释 SGD 的方式是,一开始我的 theta 参数是随机的,然后我看到了第一个样本 x1,随后我针对这个 x1 修改的我 theta,接着我看到了 x2,我再针对 x2 修改我的 theta。在等高线图中,你可能会看到,参数并没有沿着 90 度的方向下降,而是以一种更曲折的方式下降
SGD 通常不会收敛,它会振荡
还有一种下降方法是“小批量梯度下降法”,一次遍历100个样本
还有一种实践中的方法(一点点减少学习速率)
线性回归没有局部最优(在它的目标函数是误差平方和时),只有全局最优。所以,实际上你可以使用一个矩阵去表示它的参数,求cost function(目标函数)对于 参数矩阵的求导,随后让导数 = 0,求这个位置上的导数矩阵,即可直接得到全局最优解。这也叫做正态方程,这个方法仅适用于线性回归

根据吴恩达的推导,正态方程,也就是最终最优的 theta 可以通过这么一个公式求出来
如果发现 X 不可逆,那么通常意味着有多余的 features,你有某些 features 是线性相关的,你可以使用伪逆,或者找出哪些特征是线性相关的
关于怎么选择学习率:这非常依赖经验,通常我们尝试许多个不同的值,然后选择一个
相关文章:

斯坦福机器学习 Lecture2 (假设函数、参数、样本等等术语,还有批量梯度下降法、随机梯度下降法 SGD 以及它们的相关推导,还有正态方程)
假设函数定义 假设函数,猜一个 x->y 的类型,比如 y ax b,随后监督学习的任务就是找到误差最低的 a 和 b 参数 有时候我们可以定义 x0 1,来让假设函数的整个表达式一致统一 如上图是机器学习中的一些术语 额外的符号…...

【腾讯云云上实验室-向量数据库】TAI时代的数据枢纽-向量数据库 VectorDB
一、向量数据库的发展历程和时代机遇 回顾向量数据库的发展历程: 2012年开始,深度神经网络的发展催生了向量数据库的发展;2015年至2016年,Google和微软发布了标志性的论文;2017年,Facebook开源了Faiss框架…...
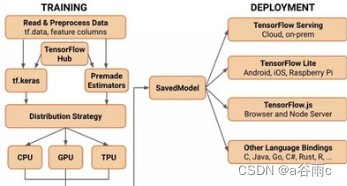
掌握深度学习利器——TensorFlow 2.x实战应用与进阶
掌握深度学习利器——TensorFlow 2.x实战应用与进阶 摘要:随着人工智能技术的飞速发展,深度学习已成为当下最热门的领域之一。作为深度学习领域的重要工具,TensorFlow 2.x 备受关注。本文将通过介绍TensorFlow 2.x的基本概念和特性ÿ…...

MySQL 之多版本并发控制 MVCC
MySQL 之多版本并发控制 MVCC 1、MVCC 中的两种读取方式1.1、快照读1.2、当前读 2、MVCC实现原理之 ReadView2.1、隐藏字段2.2、ReadView2.3、读已提交和可重复读隔离级别下,产生 ReadView 时机的区别 3、MVCC 解决幻读4、总结 MVCC(多版本并发控制&…...

优步让一切人工智能化
优步(Uber)的商业模式建立在对数据的颠覆性使用上--通过将双方智能手机的位置数据关联起来,将出租车司机与乘客配对。这意味着,它可以比传统出租车公司更快地安排司机去接乘客,极大地冲击了传统出租车公司的业务。 优步自成立以来࿰…...

DeepMind发布新模型Mirasol3B:更高效处理音频、视频数据
Google DeepMind日前悄然宣布了其人工智能研究的重大进展,推出了一款名为“Mirasol3B”的新型自回归模型,旨在提升对长视频输入的理解能力。该新模型展示了一种颠覆性的多模态学习方法,以更综合和高效的方式处理音频、视频和文本数据。 Googl…...

键盘方向键移动当前选中的table单元格,并可以输入内容
有类似于这样的表格,用的<table>标签。原本要在单元格的文本框里面输入内容,需要用鼠标一个一个去点以获取焦点,现在需要不用鼠标选中,直接用键盘的上下左右来移动当前正在输入的单元格文本框。 const currentCell React.u…...
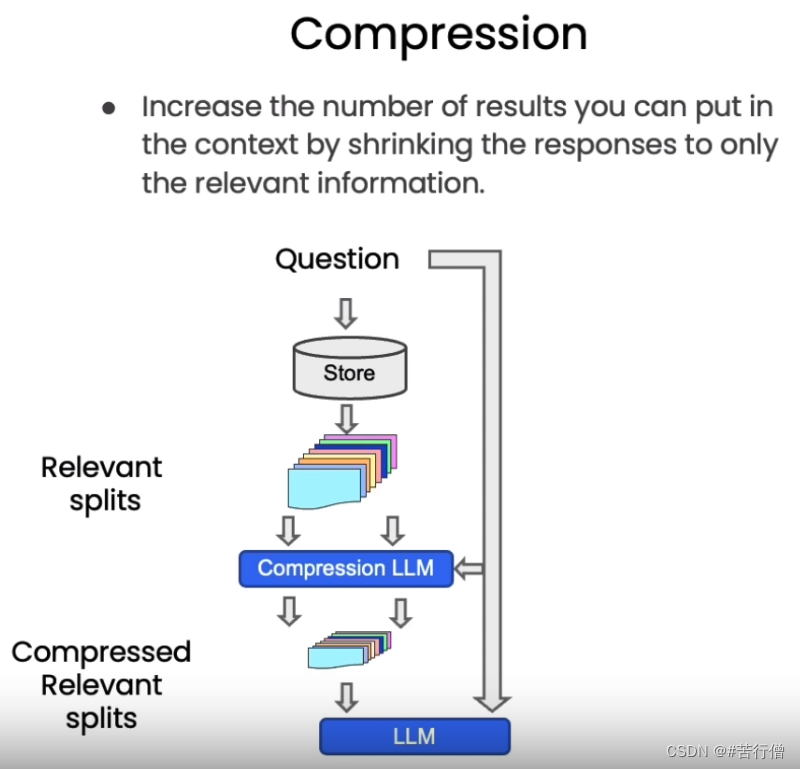
(八)、基于 LangChain 实现大模型应用程序开发 | 基于知识库的个性化问答 (检索 Retrieval)
检索增强生成(RAG)的整体工作流程如下: 在构建检索增强生成 (RAG) 系统时,信息检索是核心环节。检索是指根据用户的问题去向量数据库中搜索与问题相关的文档内容,当我们访问和查询向量数据库时可能会运用到如下几种技术…...

高效案例检索工具,Alpha案例库智慧检索成为律师检索工具首选
“工欲善其事,必先利其器。”当今,律界同仁需要权衡的问题早已不是“要不要”使用法律科技,而是如何高质量、高效率地使用法律科技工具。在业内人士看来,随着人工智能技术的不断发展,法律行业科技化将成为不可逆转的趋…...

stable diffusion十七种controlnet详细使用方法总结
个人网站:https://tianfeng.space 前言 最近不知道发点什么,做个controlnet 使用方法总结好了,如果你们对所有controlnet用法,可能了解但是有点模糊,希望能对你们有用。 一、SD controlnet 我统一下其他参数&#…...
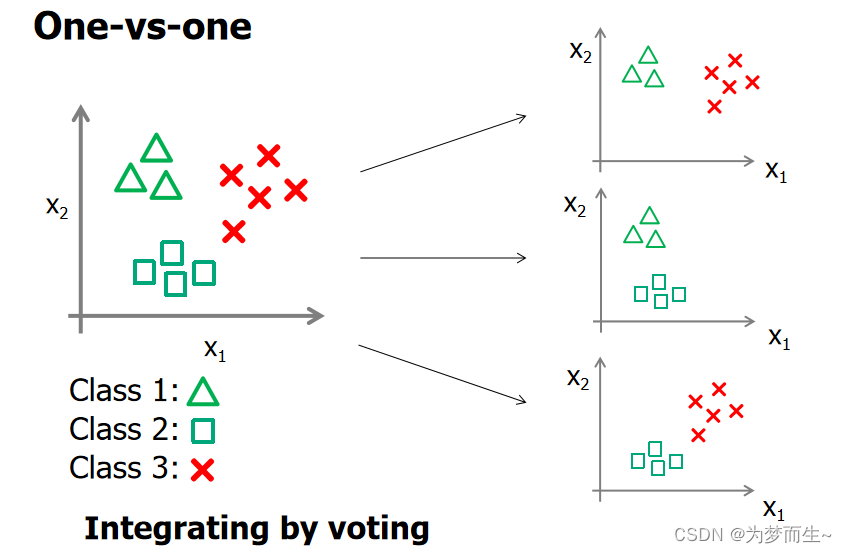
【机器学习基础】对数几率回归(logistic回归)
🚀个人主页:为梦而生~ 关注我一起学习吧! 💡专栏:机器学习 欢迎订阅!后面的内容会越来越有意思~ 💡往期推荐: 【机器学习基础】机器学习入门(1) 【机器学习基…...

团结引擎已全面支持 OpenHarmony 操作系统
Unity 中国宣布与开放原子开源基金会达成平台级战略合作。 据称团结引擎已全面支持 OpenHarmony 操作系统,同时将为 OpenHarmony 生态快速带来更多高品质游戏与实时 3D 内容。Unity 称现在用户可以 “在 OpenHarmony 框架中感受到与安卓和 iOS 同样丝滑的游戏体验”…...

【brpc学习案例实践一】rpc服务构造基本流程
前言 在crpc框架中,brpc简直越用越爽,平时工作中也常用到brpc,一直没来得及总结,抽空写点,也供自己查阅用。下附几个常用学习地址: brpc官网开源地址: https://github.com/luozesong/brpc/blob…...

Redis数据的持久化
Redis的持久化有两种方式: RDB(Redis Database)和AOF(Append Only File) 目录 一、RDB 保存方式 2、rdb在redis.conf文件中的配置 二、AOF 1、保存方式 2、aof方式持久化在redis.conf文件中的配置 三、持久化建…...

uniapp App 端 版本更新检测
function checkVersion() { var req { //升级检测数据 appid: plus.runtime.appid, version: plus.runtime.version }; const timestamp Date.parse(new Date()); config.server.query_news uni.reque…...

python用最小二乘法实现平面拟合
文章目录 数学原理代码实现测试 数学原理 平面方程可写为 A x B y C z D 0 AxByCzD0 AxByCzD0 假设 C C C不为0,则上式可以改写为 z a x b y d zaxbyd zaxbyd 则现有一组点 { p i } \{p_i\} {pi},则根据 x i , y i x_i,y_i xi,yi以及平面…...
SpringCloud微服务:Nacos和Eureka的区别
目录 配置: 区别: ephemeral设置为true时 ephemeral设置为false时(这里我使用的服务是order-service) 1. Nacos与eureka的共同点 都支持服务注册和服务拉取 都支持服务提供者心跳方式做健康检测 2. Nacos与Eu…...

基于Springboot+Vue的校园在线打印预约系统
基于SpringbootVue的校园在线打印预约系统的设计与实现 (1) 注册功能:允许学生、教职员工注册账户,并提供安全的身份验证机制,确保只有授权用户可以使用系统。 (2) 登录功能:店家或学生可以使用各自账号登录。登录后允许修改用户…...

计算机毕业设计选题推荐-掌心办公微信小程序/安卓APP-项目实战
✨作者主页:IT毕设梦工厂✨ 个人简介:曾从事计算机专业培训教学,擅长Java、Python、微信小程序、Golang、安卓Android等项目实战。接项目定制开发、代码讲解、答辩教学、文档编写、降重等。 ☑文末获取源码☑ 精彩专栏推荐⬇⬇⬇ Java项目 Py…...

1.1二分查找
二分查找,主要是针对基本有序的数据来进行查找target。 二分法的思想很简单,因为整个数组是有序的,数组默认是递增的。 1.1 使用条件 用于查找的内容逻辑上来说是需要有序的查找的数量只能是一个,而不是多个 1.2 简介 首先选…...

应用升级/灾备测试时使用guarantee 闪回点迅速回退
1.场景 应用要升级,当升级失败时,数据库回退到升级前. 要测试系统,测试完成后,数据库要回退到测试前。 相对于RMAN恢复需要很长时间, 数据库闪回只需要几分钟。 2.技术实现 数据库设置 2个db_recovery参数 创建guarantee闪回点,不需要开启数据库闪回。…...

Appium+python自动化(十六)- ADB命令
简介 Android 调试桥(adb)是多种用途的工具,该工具可以帮助你你管理设备或模拟器 的状态。 adb ( Android Debug Bridge)是一个通用命令行工具,其允许您与模拟器实例或连接的 Android 设备进行通信。它可为各种设备操作提供便利,如安装和调试…...

python/java环境配置
环境变量放一起 python: 1.首先下载Python Python下载地址:Download Python | Python.org downloads ---windows -- 64 2.安装Python 下面两个,然后自定义,全选 可以把前4个选上 3.环境配置 1)搜高级系统设置 2…...

HTML前端开发:JavaScript 常用事件详解
作为前端开发的核心,JavaScript 事件是用户与网页交互的基础。以下是常见事件的详细说明和用法示例: 1. onclick - 点击事件 当元素被单击时触发(左键点击) button.onclick function() {alert("按钮被点击了!&…...
)
【RockeMQ】第2节|RocketMQ快速实战以及核⼼概念详解(二)
升级Dledger高可用集群 一、主从架构的不足与Dledger的定位 主从架构缺陷 数据备份依赖Slave节点,但无自动故障转移能力,Master宕机后需人工切换,期间消息可能无法读取。Slave仅存储数据,无法主动升级为Master响应请求ÿ…...

Springboot社区养老保险系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,社区养老保险系统小程序被用户普遍使用,为方…...
:观察者模式)
JS设计模式(4):观察者模式
JS设计模式(4):观察者模式 一、引入 在开发中,我们经常会遇到这样的场景:一个对象的状态变化需要自动通知其他对象,比如: 电商平台中,商品库存变化时需要通知所有订阅该商品的用户;新闻网站中࿰…...

c# 局部函数 定义、功能与示例
C# 局部函数:定义、功能与示例 1. 定义与功能 局部函数(Local Function)是嵌套在另一个方法内部的私有方法,仅在包含它的方法内可见。 • 作用:封装仅用于当前方法的逻辑,避免污染类作用域,提升…...

es6+和css3新增的特性有哪些
一:ECMAScript 新特性(ES6) ES6 (2015) - 革命性更新 1,记住的方法,从一个方法里面用到了哪些技术 1,let /const块级作用域声明2,**默认参数**:函数参数可以设置默认值。3&#x…...

sshd代码修改banner
sshd服务连接之后会收到字符串: SSH-2.0-OpenSSH_9.5 容易被hacker识别此服务为sshd服务。 是否可以通过修改此banner达到让人无法识别此服务的目的呢? 不能。因为这是写的SSH的协议中的。 也就是协议规定了banner必须这么写。 SSH- 开头,…...
