【机器学习基础】对数几率回归(logistic回归)
🚀个人主页:为梦而生~ 关注我一起学习吧!
💡专栏:机器学习 欢迎订阅!后面的内容会越来越有意思~
💡往期推荐:
【机器学习基础】机器学习入门(1)
【机器学习基础】机器学习入门(2)
【机器学习基础】机器学习的基本术语
【机器学习基础】机器学习的模型评估(评估方法及性能度量原理及主要公式)
【机器学习基础】一元线性回归(适合初学者的保姆级文章)
【机器学习基础】多元线性回归(适合初学者的保姆级文章)
💡本期内容:Logistic回归和对数几率回归是同一个模型,是统计学习中的经典分类方法,属于对数线性模型。上一节讨论了如何使用线性模型进行回归学习,但若要做的是分类任务该怎么办?答案蕴涵在线性回归广义线性模型(假设函数)中:只需找一个单调可微函数将分类任务的真实标记y与线性回归模型的预测值联系起来。超级基础的文章,赶紧收藏学习吧!!!
文章目录
- 1 什么是对数几率回归
- 2 假设函数
- 3 决策边界
- 4 代价函数
- 4.1 与线性回归模型的区别
- 4.2 重新定义代价函数
- 5 如何处理多分类问题
- 5.1 一对多法(one-versus-rest,简称OVR SVMs)
- 5.2 一对一的投票策略(One-vs-one)
1 什么是对数几率回归
对数几率回归,也称为逻辑回归,是一种广义线性模型。在逻辑回归中,通过使用sigmoid函数,将线性回归的输出映射到0和1之间,表示样本属于某一类的概率。所以它属于分类模型。
逻辑回归模型的训练通常通过最大化似然函数来完成,常用的解决方法是使用梯度下降算法进行模型优化,通过迭代调整模型参数,使得模型的预测结果逐渐接近实际标签。
逻辑回归可以表示为一个关于θ的函数hθ(x),即hθ(x) = P(y=1|x;θ),表示给定特征x和参数θ的条件下,样本属于正例的概率。
由于它属于一个分类模型,所以它的输出应该具有分类的性质,于是,这里规定其输出永远在0,1之间。
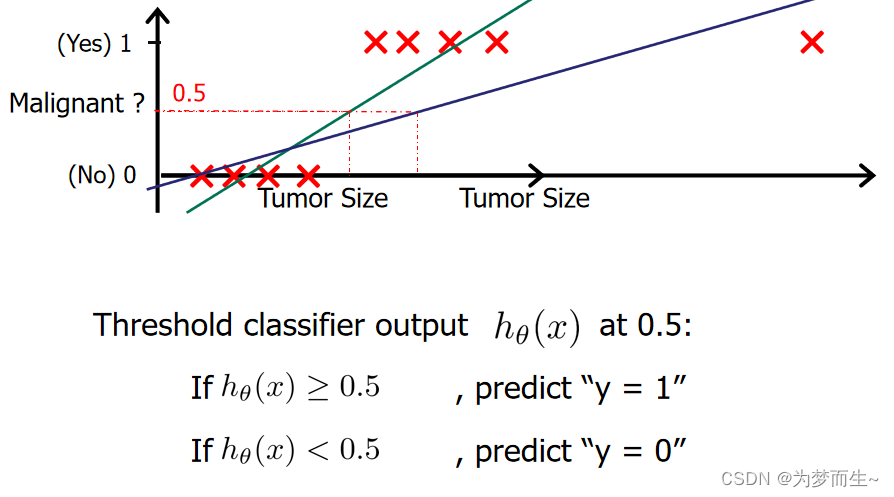
2 假设函数
考虑二分类任务,其输出标记 y∈{0, 1},而线性回归模型产生的预测值 h θ ( x ) h_{\theta }(x) hθ(x)是实值,于是,我们需将实值 z z z转换为 0/1值最理想的是“单位阶跃函数”(unit-step function)

但阶跃函数并不连续,于是我们希望找到能在一定程度上近似单位阶跃函数的“替代函数”(surrogate function),并希望它单调可微对数几率函数(logistic function)正是这样一个常用的替代函数:

那么对数几率回归的假设函数应该将输出控制到0~1之间,于是就有了大名鼎鼎的sigmoid函数:

- 对于假设函数在对数几率回归的解释:
h θ ( x ) h_{\theta }(x) hθ(x)的作用是:对于给定的输入变量,根据选择的参数计算输出变量=1的可能性。即 h θ ( x ) h_{\theta }(x) hθ(x)带有一定的概率含义。
例如,对于给定的x,通过已知的参数计算出 h θ = 0.7 h_{\theta }=0.7 hθ=0.7,则表示有70%的概率y为正例.
若将 y y y视为样本 x x x作为正例的可能性,则 1 − y 1-y 1−y 是其反例可能性,两者的比值 y 1 − y \frac{y}{1-y} 1−yy称为"几率" (odds) ,反映了 x x x作为正例的相对可能性. 对几率取对数则得到"对数几率" (log odds ,亦称 logit)

由此可看出,式(3.18) 实际上是在用线性回归模型的预测结果去逼近真实标记的对数几率,因此,其对应的模型称为"对数几率回归" (logistic regression ,亦称 logit regression) .
3 决策边界
在对数几率回归中,我们预测:
当hθ(x)>=0.5
时,预测y=1.
当hθ(x)<0.5
时,预测y=0.
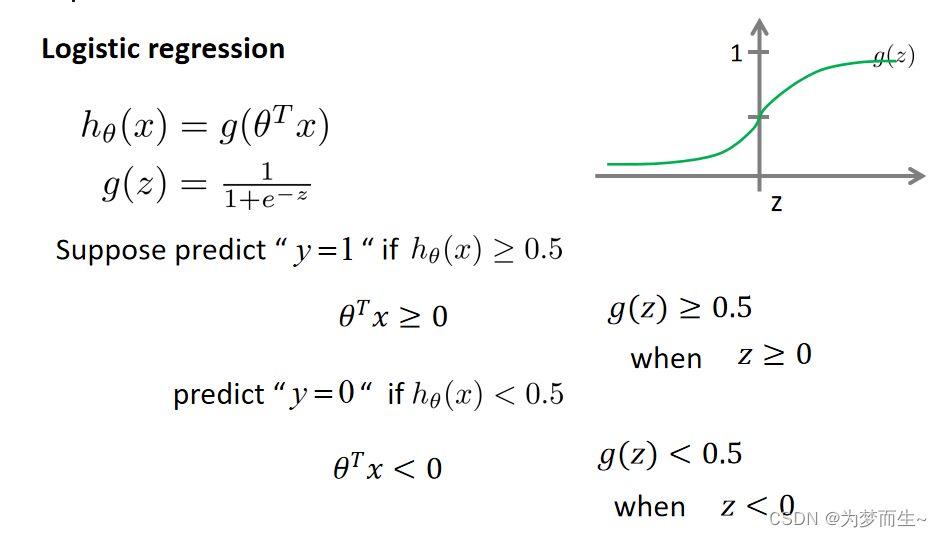
根据上面绘制的图像,我们知道:
当z>=0时,g(z)>=0.5
当z<0时,g(z)<0.5
- 举个例子
当参数 θ \theta θ是向量 [ − 3 , 1 , 1 ] [-3,1,1] [−3,1,1]。 则当 − 3 + x 1 + x 2 = 0 -3 +x_1+x_2= 0 −3+x1+x2=0时,模型将预测 y=1。我们可以绘制这条线便是我们模型的分界线,将预测为 1 的区域和预测为 0 的区域分隔开.
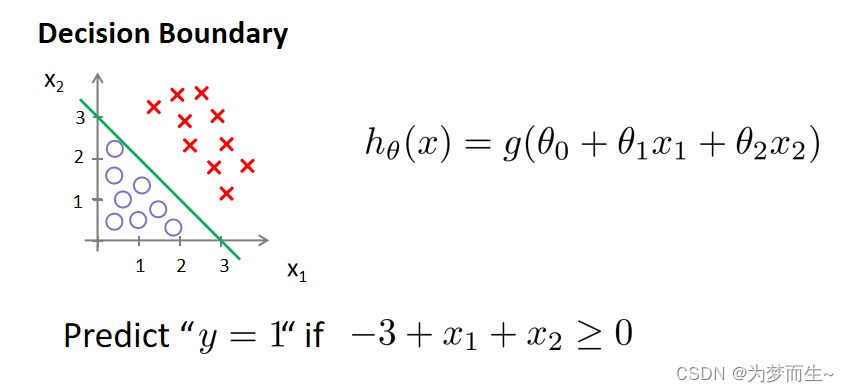
换句话说,大于这条线的部分预测y=0,小于这条线的部分预测y=0. 这条线就叫做决策边界。
4 代价函数
4.1 与线性回归模型的区别
对于线性回归,我们知道它的代价函数为 J ( θ ) = 1 2 m Σ i = 1 m ( h θ x ( i ) − y ( i ) ) 2 J(\theta )=\frac{1}{2m}\Sigma _{i=1}^{m}(h_{\theta }x^{(i)}-y^{(i)})^{2} J(θ)=2m1Σi=1m(hθx(i)−y(i))2, 我们可以对其进行梯度下降求最小值。其中可以用梯度下降最根本的原因在于它是一个凸函数,如下图所示

在逻辑回归中,如果还用和线性回归一样的代价函数的话,是求不到全局的最小值的,只能求到局部的最小值。这是因为,逻辑回归的假设函数变成了 h θ ( x ) = g ( θ T x ) = g ( z ) = 1 1 + e − z = 1 1 + e − θ T x h_{\theta }(x)=g(\theta ^{T}x)=g(z)=\frac{1}{1+e^{-z}}=\frac{1}{1+e^{-\theta ^{T}x}} hθ(x)=g(θTx)=g(z)=1+e−z1=1+e−θTx1,将其带入上面的代价函数,可得到它的图像为:

由此我们知道,我们需要重新定义逻辑回归的代价函数。且这个代价函数一定是一个凸函数,否则不方便使用梯度下降求最小值。
4.2 重新定义代价函数
这里我们定义新的代价函数为:
J ( θ ) = 1 m Σ i = 1 m c o s t ( h θ ( x ( i ) ) , y ( i ) ) J(\theta )=\frac{1}{m}\Sigma _{i=1}^{m}cost(h_{\theta }(x^{(i)}),y^{(i)}) J(θ)=m1Σi=1mcost(hθ(x(i)),y(i))

这样分条件构建代价函数,可以使得当实际的 𝑦 = 1 且ℎ𝜃(𝑥)也为 1 时误差为 0, 当 𝑦 = 1 但ℎ𝜃(𝑥)不为 1 时误差随着ℎ𝜃(𝑥)变小而变大;当实际的 𝑦 = 0 且ℎ𝜃(𝑥)也为 0 时 代价为 0,当𝑦 = 0 但ℎ𝜃(𝑥)不为 0 时误差随着 ℎ𝜃(𝑥)的变大而变大。
由此可以保证它的输出用于分类
对其进行化简:

在得到这样一个代价函数以后,我们便可以用梯度下降法来求得代价函数取最小值时的参数了。方法和前面的线性回归求梯度下降差不多。

5 如何处理多分类问题
现实生活中,我们遇到的问题往往是很多类别的东西需要分类,所以如何利用二分类的模型解决多分类问题呢?
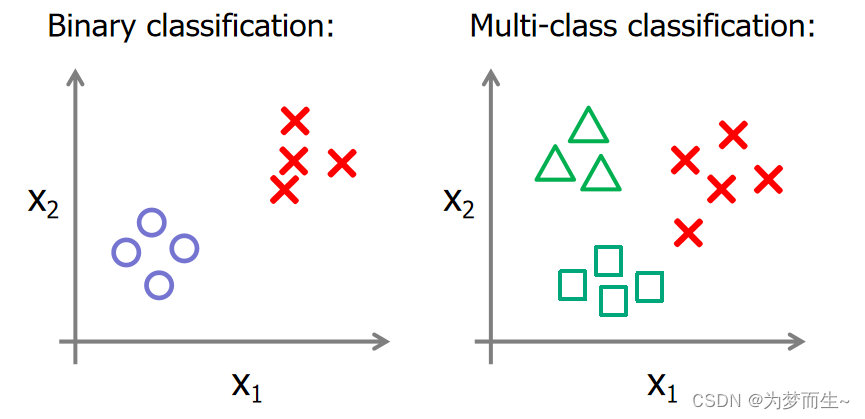
5.1 一对多法(one-versus-rest,简称OVR SVMs)
训练时依次把某个类别的样本归为一类,其他剩余的样本归为另一类,这样k个类别的样本就构造出了k个SVM。分类时将未知样本分类为具有最大分类函数值的那类。
假如我有四类要划分(也就是4个Label),他们是A、B、C、D。
于是我在抽取训练集的时候,分别抽取
- A所对应的向量作为正集,B,C,D所对应的向量作为负集;
- B所对应的向量作为正集,A,C,D所对应的向量作为负集;
- C所对应的向量作为正集,A,B,D所对应的向量作为负集;
- D所对应的向量作为正集,A,B,C所对应的向量作为负集;
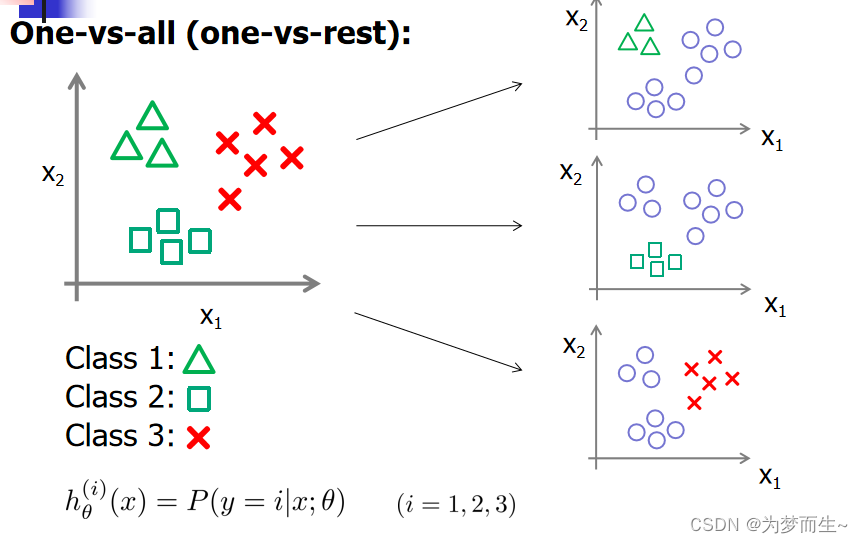
使用这四个训练集分别进行训练,然后的得到四个训练结果文件。在测试的时候,把对应的测试向量分别利用这四个训练结果文件进行测试。最后每个测试都有一个结果f1(x),f2(x),f3(x),f4(x)。
于是最终的结果便是这四个值中最大的一个作为分类结果。
- 评价:
这种方法有种缺陷,因为训练集是1:M,这种情况下存在biased.因而不是很实用。可以在抽取数据集的时候,从完整的负集中再抽取三分之一作为训练负集。
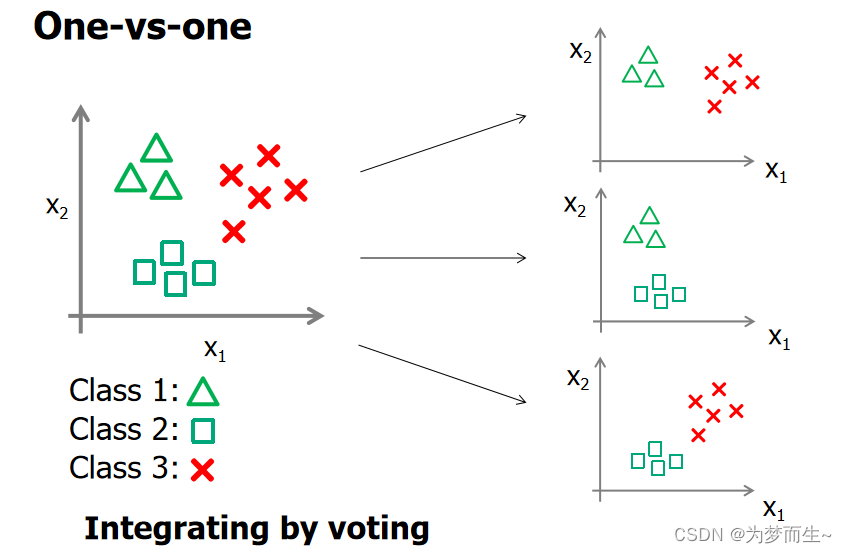
5.2 一对一的投票策略(One-vs-one)
分类器的选择:
- 将A、 B、C、 D四类样本两类两类地组成训练集, 即(A,B)、(A.C)、(A,D)、(B,C)、(B,D)、(C,D), 得到6个(对于n类问题,为n(n-1)/2个)SVM二分器。
- 在测试的时候,把测试样本又依次送入这6个二分类器, 采取投票形式, 最后得到一组结果。
投票是以如下方式进行的。
-
初始化:vote(A)= vote(B)= vote( C )= vote(D)=0。
-
投票过程:
(1)如果使用训练集(A,B)得到的分类器将一个测试样本判定为A类,则vote(A)=vote(A)+1 ,否则vote(B)=vote(B)+ 1;
(2)如果使用(A,C)训练的分类器将又判定为A类,则vote(A)=vote(A)+1, 否则vote( C )=vote( C )+1;
(3)… ;
(4)如果使用(C,D)训练的分类器将又判定为C类,则vote( C )=vote( C )+ 1 , 否则vote(D)=vote(D)+ 1。
-
最终判决:
Max(vote(A), vote(B), vote( C ), vote(D))。
如有两个以上的最大值,则一般可简单地取第一个最大值所对应的类
相关文章:

【机器学习基础】对数几率回归(logistic回归)
🚀个人主页:为梦而生~ 关注我一起学习吧! 💡专栏:机器学习 欢迎订阅!后面的内容会越来越有意思~ 💡往期推荐: 【机器学习基础】机器学习入门(1) 【机器学习基…...

团结引擎已全面支持 OpenHarmony 操作系统
Unity 中国宣布与开放原子开源基金会达成平台级战略合作。 据称团结引擎已全面支持 OpenHarmony 操作系统,同时将为 OpenHarmony 生态快速带来更多高品质游戏与实时 3D 内容。Unity 称现在用户可以 “在 OpenHarmony 框架中感受到与安卓和 iOS 同样丝滑的游戏体验”…...

【brpc学习案例实践一】rpc服务构造基本流程
前言 在crpc框架中,brpc简直越用越爽,平时工作中也常用到brpc,一直没来得及总结,抽空写点,也供自己查阅用。下附几个常用学习地址: brpc官网开源地址: https://github.com/luozesong/brpc/blob…...

Redis数据的持久化
Redis的持久化有两种方式: RDB(Redis Database)和AOF(Append Only File) 目录 一、RDB 保存方式 2、rdb在redis.conf文件中的配置 二、AOF 1、保存方式 2、aof方式持久化在redis.conf文件中的配置 三、持久化建…...

uniapp App 端 版本更新检测
function checkVersion() { var req { //升级检测数据 appid: plus.runtime.appid, version: plus.runtime.version }; const timestamp Date.parse(new Date()); config.server.query_news uni.reque…...

python用最小二乘法实现平面拟合
文章目录 数学原理代码实现测试 数学原理 平面方程可写为 A x B y C z D 0 AxByCzD0 AxByCzD0 假设 C C C不为0,则上式可以改写为 z a x b y d zaxbyd zaxbyd 则现有一组点 { p i } \{p_i\} {pi},则根据 x i , y i x_i,y_i xi,yi以及平面…...
SpringCloud微服务:Nacos和Eureka的区别
目录 配置: 区别: ephemeral设置为true时 ephemeral设置为false时(这里我使用的服务是order-service) 1. Nacos与eureka的共同点 都支持服务注册和服务拉取 都支持服务提供者心跳方式做健康检测 2. Nacos与Eu…...

基于Springboot+Vue的校园在线打印预约系统
基于SpringbootVue的校园在线打印预约系统的设计与实现 (1) 注册功能:允许学生、教职员工注册账户,并提供安全的身份验证机制,确保只有授权用户可以使用系统。 (2) 登录功能:店家或学生可以使用各自账号登录。登录后允许修改用户…...

计算机毕业设计选题推荐-掌心办公微信小程序/安卓APP-项目实战
✨作者主页:IT毕设梦工厂✨ 个人简介:曾从事计算机专业培训教学,擅长Java、Python、微信小程序、Golang、安卓Android等项目实战。接项目定制开发、代码讲解、答辩教学、文档编写、降重等。 ☑文末获取源码☑ 精彩专栏推荐⬇⬇⬇ Java项目 Py…...

1.1二分查找
二分查找,主要是针对基本有序的数据来进行查找target。 二分法的思想很简单,因为整个数组是有序的,数组默认是递增的。 1.1 使用条件 用于查找的内容逻辑上来说是需要有序的查找的数量只能是一个,而不是多个 1.2 简介 首先选…...

提升工作效率,打造精细思维——OmniOutliner 5 Pro for Mac
在当今快节奏的工作环境中,如何高效地组织和管理我们的思维和任务成为了关键。而OmniOutliner 5 Pro for Mac正是为此而生的一款强大工具。无论你是专业写作者、项目经理还是学生,OmniOutliner 5 Pro for Mac都能帮助你提升工作效率,打造精细…...
idea显示pom.xml文件漂黄警告 Dependency maven:xxx:xxx is vulnerable
场景: idea警告某些maven依赖包有漏洞或者依赖传递有易受攻击包,如下: 解决: 1、打开idea设置,找到 File | Settings | Editor | Inspections 2、取消上述两项勾选即可...

Linux中安装部署环境(JAVA)
目录 在Linux中安装jdk 包管理器yum安装jdk JDK安装过程中的问题 验证安装jdk 在Linux中安装tomcat 安装mysql 在Linux中安装jdk jdk在Linux中的安装方式有很多种, 这里介绍最简单的方法, 也就是包管理器方法: 包管理器yum安装jdk Linux中常见的包管理器有: yumaptp…...
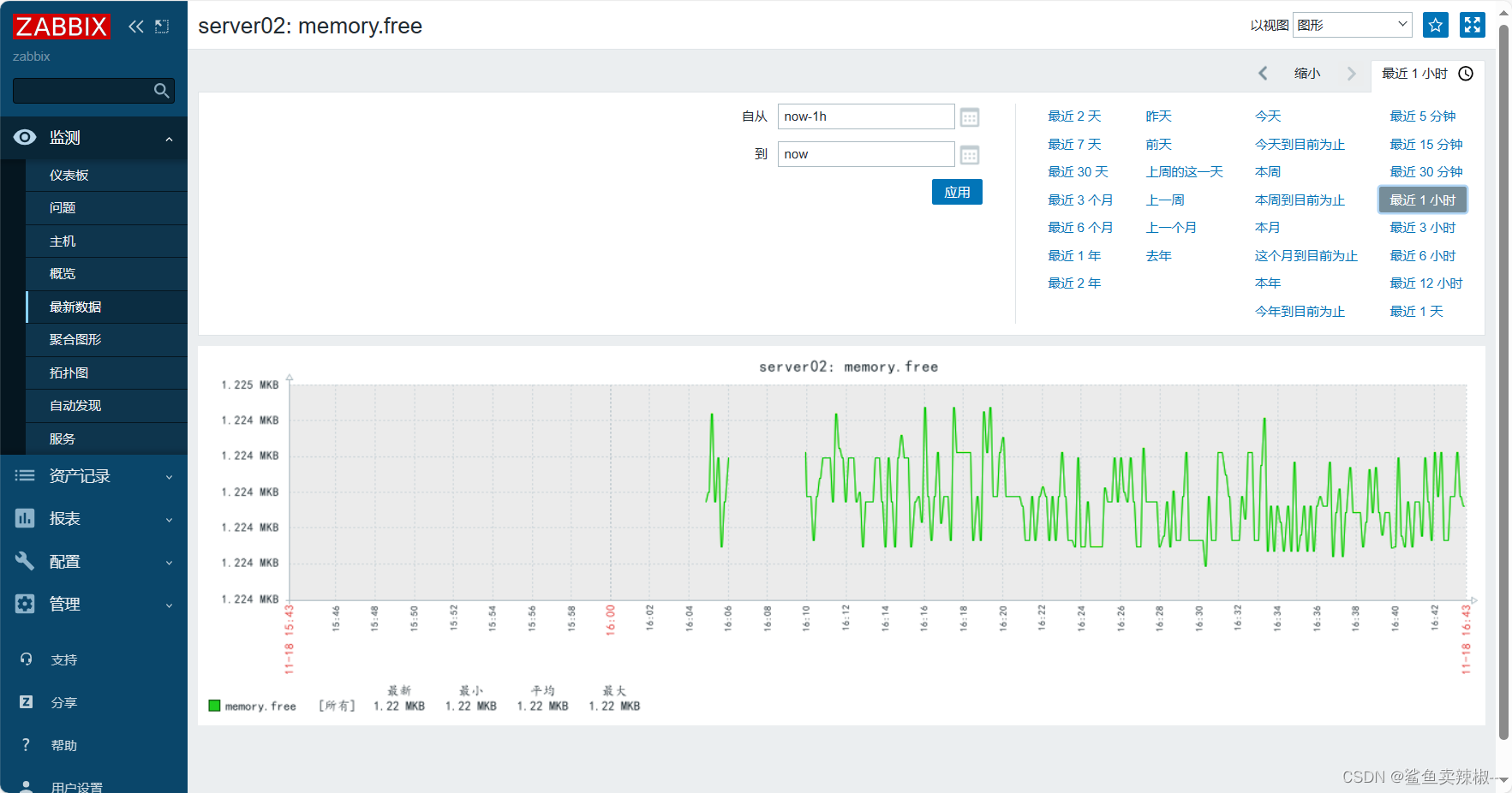
Zabbix Proxy分布式监控
目录 Zabbix Proxy简介 实验环境 proxy端配置 1.安装仓库 2.安装zabbix-proxy 3.创建初始数据库 4.导入初始架构和数据,系统将提示您输入新创建的密码 5.编辑配置文件 /etc/zabbix/zabbix_proxy.conf,配置完成后要重启。 agent客户端配置 zabbix…...

前端设计模式之【代理模式】
文章目录 前言介绍例子场景优缺点标题五后言 前言 hello world欢迎来到前端的新世界 😜当前文章系列专栏:前端设计模式 🐱👓博主在前端领域还有很多知识和技术需要掌握,正在不断努力填补技术短板。(如果出现错误&…...

Canal+Kafka实现MySQL与Redis数据同步(二)
CanalKafka实现MySQL与Redis数据同步(二) 创建MQ消费者进行同步 在application.yml配置文件加上kafka的配置信息: spring:kafka:# Kafka服务地址bootstrap-servers: 127.0.0.1:9092consumer:# 指定一个默认的组名group-id: consumer-group…...

NOIP2023模拟19联测40 诡异键盘
题目大意 有一个键盘,上面有 n 1 n1 n1个按键,按下按键 1 ≤ i ≤ n 1\leq i\leq n 1≤i≤n会打印出字符串 S i S_i Si,按下按键 n 1 n1 n1会删掉结尾的 K K K个字符,如果不足 K K K个字符则全部删完,问打印出 S …...
)
算法设计与分析 | 众数问题(c语言)
题目 所谓众数,就是对于给定的含有N个元素的多重集合,每个元素在S中出现次数最多的成为该元素的重数, 多重集合S重的重数最大的元素成为众数。例如:S{1,2,2,2,3,5},则多重集S的众数是2,其重数为3。 现在你…...

sql server外键设置
SQL Server外键设置 简介 在关系型数据库中,外键是一种约束,用于确保数据的完整性和一致性。外键约束定义了一个表中的列与另一个表中的列之间的关系,它可以用来保证数据的一致性、防止数据的破坏和数据冗余。在SQL Server中,我们…...
)
R语言实现多变量孟德尔随机化分析(1)
多变量孟德尔随机化分析调整了潜在混杂因素的影响。 1、调整哪些因素?参考以往文献。可以分别调整,也可以一起调整。 2、解决了什么问题?某个暴露相关的SNP,往往与某个或者某几个混杂因素相关。可以控制混杂偏倚。 3、如何解释…...

设计模式和设计原则回顾
设计模式和设计原则回顾 23种设计模式是设计原则的完美体现,设计原则设计原则是设计模式的理论基石, 设计模式 在经典的设计模式分类中(如《设计模式:可复用面向对象软件的基础》一书中),总共有23种设计模式,分为三大类: 一、创建型模式(5种) 1. 单例模式(Sing…...

大话软工笔记—需求分析概述
需求分析,就是要对需求调研收集到的资料信息逐个地进行拆分、研究,从大量的不确定“需求”中确定出哪些需求最终要转换为确定的“功能需求”。 需求分析的作用非常重要,后续设计的依据主要来自于需求分析的成果,包括: 项目的目的…...

ubuntu搭建nfs服务centos挂载访问
在Ubuntu上设置NFS服务器 在Ubuntu上,你可以使用apt包管理器来安装NFS服务器。打开终端并运行: sudo apt update sudo apt install nfs-kernel-server创建共享目录 创建一个目录用于共享,例如/shared: sudo mkdir /shared sud…...

Python爬虫实战:研究feedparser库相关技术
1. 引言 1.1 研究背景与意义 在当今信息爆炸的时代,互联网上存在着海量的信息资源。RSS(Really Simple Syndication)作为一种标准化的信息聚合技术,被广泛用于网站内容的发布和订阅。通过 RSS,用户可以方便地获取网站更新的内容,而无需频繁访问各个网站。 然而,互联网…...

聊聊 Pulsar:Producer 源码解析
一、前言 Apache Pulsar 是一个企业级的开源分布式消息传递平台,以其高性能、可扩展性和存储计算分离架构在消息队列和流处理领域独树一帜。在 Pulsar 的核心架构中,Producer(生产者) 是连接客户端应用与消息队列的第一步。生产者…...

Android 之 kotlin 语言学习笔记三(Kotlin-Java 互操作)
参考官方文档:https://developer.android.google.cn/kotlin/interop?hlzh-cn 一、Java(供 Kotlin 使用) 1、不得使用硬关键字 不要使用 Kotlin 的任何硬关键字作为方法的名称 或字段。允许使用 Kotlin 的软关键字、修饰符关键字和特殊标识…...
)
Typeerror: cannot read properties of undefined (reading ‘XXX‘)
最近需要在离线机器上运行软件,所以得把软件用docker打包起来,大部分功能都没问题,出了一个奇怪的事情。同样的代码,在本机上用vscode可以运行起来,但是打包之后在docker里出现了问题。使用的是dialog组件,…...

基于SpringBoot在线拍卖系统的设计和实现
摘 要 随着社会的发展,社会的各行各业都在利用信息化时代的优势。计算机的优势和普及使得各种信息系统的开发成为必需。 在线拍卖系统,主要的模块包括管理员;首页、个人中心、用户管理、商品类型管理、拍卖商品管理、历史竞拍管理、竞拍订单…...

pycharm 设置环境出错
pycharm 设置环境出错 pycharm 新建项目,设置虚拟环境,出错 pycharm 出错 Cannot open Local Failed to start [powershell.exe, -NoExit, -ExecutionPolicy, Bypass, -File, C:\Program Files\JetBrains\PyCharm 2024.1.3\plugins\terminal\shell-int…...

VisualXML全新升级 | 新增数据库编辑功能
VisualXML是一个功能强大的网络总线设计工具,专注于简化汽车电子系统中复杂的网络数据设计操作。它支持多种主流总线网络格式的数据编辑(如DBC、LDF、ARXML、HEX等),并能够基于Excel表格的方式生成和转换多种数据库文件。由此&…...
