Kotlin 知识体系
Kotlin 知识体系
- 1、Kotlin 文档
- 2、Kotlin 基础
- 3、桌面应用程序
- 4、Android 与 iOS 应用程序
1、Kotlin 文档

Kotlin 是一门现代但已成熟的编程语言,旨在让开发人员更幸福快乐。 它简洁、安全、可与 Java 及其他语言互操作,并提供了多种方式在多个平台间复用代码,以实现高效编程。
https://kotlinlang.org/
Kotlin docs
Kotlin 官方文档 中文版
Kotlin 多平台
Android 与 iOS 应用程序: 借助 Compose 多平台 (JetBrains 开发的基于 Kotlin 的声明式 UI 框架), 还可以跨 Android 与 iOS 共享 UI 来创建完全跨平台的应用。尝试使用这个 Compose 多平台移动端应用程序模板 来创建自己的移动应用程序,并在两个平台间共享 UI。
桌面应用程序: Compose 多平台有助于跨桌面平台(如 Windows、macOS 与 Linux)共享 UI。 包括 JetBrains Toolbox 应用 在内的许多应用程序都已经采用了这种方式。尝试使用这个 Compose 多平台桌面应用程序模板 来创建自己的项目,并在桌面平台间共享 UI。
Android 知识体系 5.1Kotlin
Android 的 Kotlin 优先方法:在 2019 年 Google I/O 大会上,我们宣布今后将优先采用 Kotlin 进行 Android 开发,并且也坚守了这一承诺。Kotlin 是一种富有表现力且简洁的编程语言,不仅可以减少常见代码错误,还可以轻松集成到现有应用中。如果您想构建 Android 应用,建议您从 Kotlin 开始着手,充分利用一流的 Kotlin 功能。
使用 Jetpack Compose 更快地打造更出色的应用
2、Kotlin 基础
Kotlin 入门
Kotlin 教程 | 菜鸟教程
| Kotlin对比java | 抛弃 Java 改用 Kotlin 的六个月后,我后悔了 |
3、桌面应用程序
Compose 多平台桌面应用程序模板
4、Android 与 iOS 应用程序
Android 知识体系 5.1Kotlin
Compose 多平台移动端应用程序模板
相关文章:

Kotlin 知识体系
Kotlin 知识体系 1、Kotlin 文档2、Kotlin 基础3、桌面应用程序4、Android 与 iOS 应用程序 1、Kotlin 文档 Kotlin 是一门现代但已成熟的编程语言,旨在让开发人员更幸福快乐。 它简洁、安全、可与 Java 及其他语言互操作,并提供了多种方式在多个平台间复…...
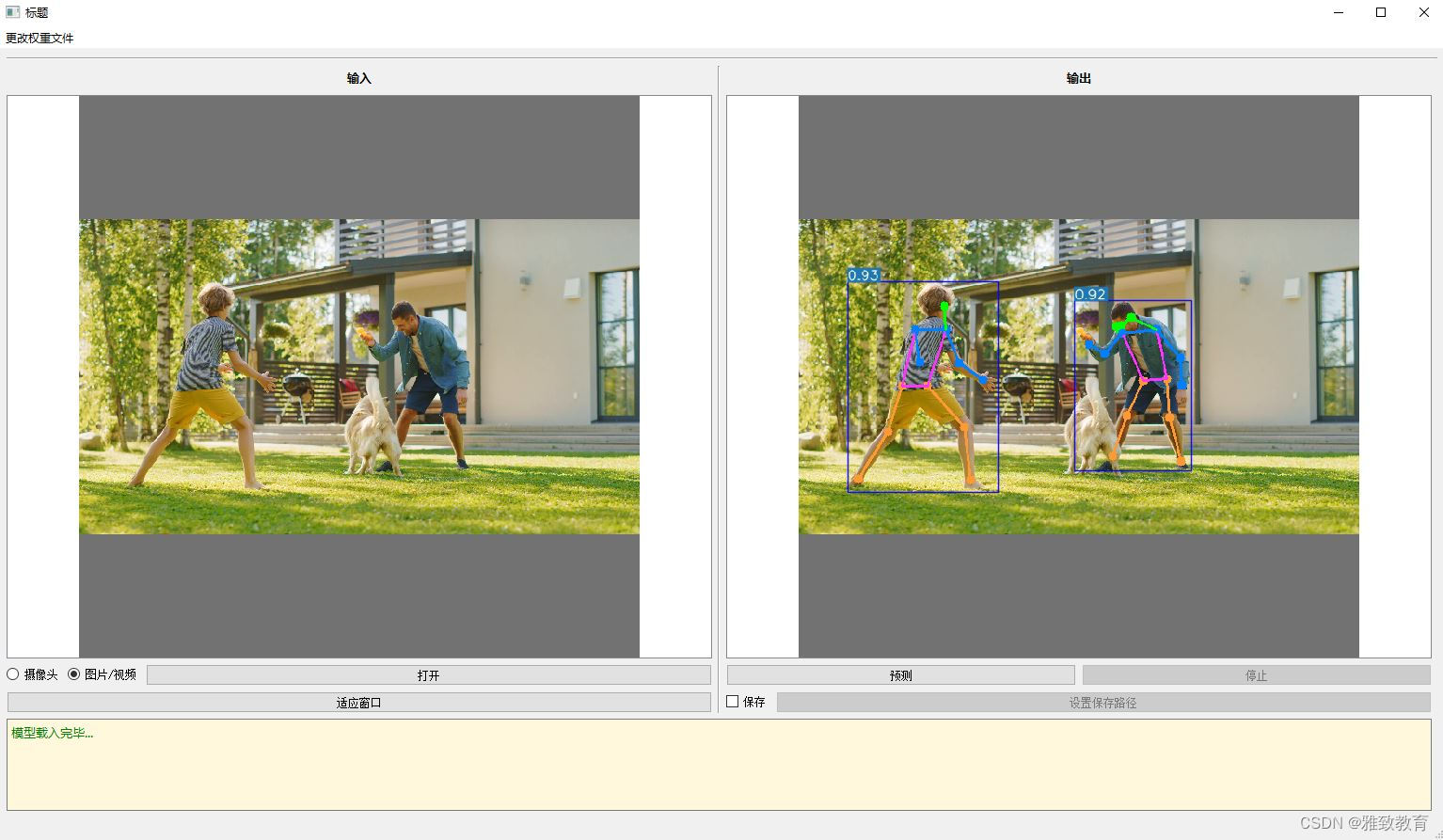
深度学习之基于YoloV5-Pose的人体姿态检测可视化系统
欢迎大家点赞、收藏、关注、评论啦 ,由于篇幅有限,只展示了部分核心代码。 文章目录 一项目简介 深度学习之基于 YOLOv5-Pose 的人体姿态检测可视化系统介绍YOLOv5-Pose 简介系统特点系统架构使用方法 二、功能三、系统四. 总结 一项目简介 深度学习之基…...

为什么Go是后端开发的未来
近年来,Go 编程语言的流行度迅速增加。Go 最初由 Google 开发,迅速成为后端开发中最受欢迎的语言之一,特别是在分布式系统和微服务的开发中。本文将讨论为什么 Go 是后端开发的未来。 Go 简介 Go,又称为 Golang,是由…...

Linux输入设备应用编程(键盘,按键,触摸屏,鼠标)
目录 一 输入设备编程介绍 1.1 什么是输入设备呢? 1.2 什么是输入设备的应用编程? 1.3 input子系统 1.4 数据读取流程 1.5 应用程序如何解析数据 1.5.1 按键类事件: 1.5.2 相对位移事件 1.5.3 绝对位移事件 二 读取 struct input_e…...

【Axure教程】滑动内容选择器
滑动内容选择器通常是一种用户界面组件,允许用户通过滑动手势在一组内容之间进行选择。这种组件可以在移动应用程序或网页中使用,以提供直观的图片选择体验。 那今天就教大家如何用中继器制作一个滑动内容选择器,我们会以滑动选择电影为案例…...

vite+vue3使用@路径,报错处理
报错原因:未配置 符号为指定路径别名,直接使用导致 处理方法: 安装path模块: npm install --save-dev types/node修改vite.config.ts import { defineConfig } from vite import vue from vitejs/plugin-vue import path from…...
[开源]基于 AI 大语言模型 API 实现的 AI 助手全套开源解决方案
原文:[开源]基于 AI 大语言模型 API 实现的 AI 助手全套开源解决方案 一飞开源,介绍创意、新奇、有趣、实用的开源应用、系统、软件、硬件及技术,一个探索、发现、分享、使用与互动交流的开源技术社区平台。致力于打造活力开源社区࿰…...
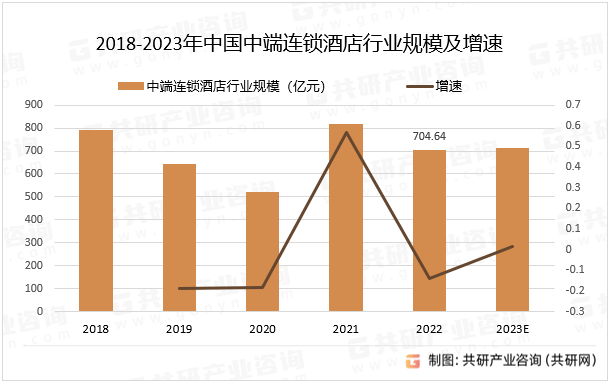
2023年中国中端连锁酒店分类、市场规模及主要企业市占率[图]
中端连锁酒店行业是指定位于中档酒店市场、具有全国统一的品牌形象识别系统、全国统一的运营体系、会员体系和营销体系的酒店。中端酒店通常提供舒适、标准化的房间设施和服务,价格较为合理,符合广大消费者的需求。其价格略高于经济型酒店,但…...
mac下vue-cli从2.9.6升级到最新版本
由于mac之前安装了 vue 2.9.6 的版本,现在想升级到最新版本,用官方给的命令: npm uninstall vue-cli -g 发现不行。 1、究其原因:从vue-cli 3.0版本开始原来的npm install -g vue-cli 安装的都是旧版,最高到2.9.6。安…...
【cpolar】搭建我的世界Java版服务器,公网远程联机
🎥 个人主页:深鱼~🔥收录专栏:cpolar🌄欢迎 👍点赞✍评论⭐收藏 目录 前言: 1. 搭建我的世界服务器 1.1 服务器安装java环境 1.2 配置服务端 2. 测试局域网联机 3. 公网远程联机 3.1 安…...

Redis数据类型–Geospatial 地理空间
目录 前言 命令 1、geoadd 1)格式 2)实例 2、geopos 1)格式 2)实例 3、geodist 1)格式 2)实例 4、georadius 1)格式 2)实例 前言 Redis 3.2 中增加了对GEO类型的支持。GEO…...

LeetCode 面试题 16.26. 计算器
文章目录 一、题目二、C# 题解 一、题目 给定一个包含正整数、加()、减(-)、乘(*)、除(/)的算数表达式(括号除外),计算其结果。 表达式仅包含非负整数,, - ,*,/ 四种运算符和空格 。 整数除法仅保留整数部分。 示例 …...

15篇MyBatis-Plus系列集合篇「值得收藏学习」
历史文章(文章累计490) 《国内最全的Spring Boot系列之一》 《国内最全的Spring Boot系列之二》 《国内最全的Spring Boot系列之三》 《国内最全的Spring Boot系列之四》 《国内最全的Spring Boot系列之五》 《国内最全的Spring Boot系列之六》 M…...
: 结构体、ref struct)
C#入门(6): 结构体、ref struct
文章目录 定义结构体实例化结构体结构体的值类型特性结构体和类的区别限制ref structref return C# 中的结构体(Struct)是一种值类型数据结构,用于封装不同或相同类型的数据成一个单一的实体。结构体非常适合用来表示轻量级的对象,…...

Java shp 转 GeoJson
文章目录 1. 依赖安装1.1 配置软件源1.2 引入依赖 2. 功能实现3. 参考链接 1. 依赖安装 1.1 配置软件源 在项目 pom.xml 添加, maven 的 settings.xml 配置的源,mirrorOf 不能是 *,不然安装不上 <project>...<repositories><repository><id…...

shadow复习之planar shadow
planar shadow 通常来说 shadow都是画一个map 这个map有个很大的问题,那就是size有问题 你希望有很高的精度,就必定要用大size的图片,这显然是不太妙的 那么这里就出现一个取巧的法子,如果你只考虑投影到平面上,光源是…...

计算机视觉的应用17-利用CrowdCountNet模型解决人群数量计算问题(pytorch搭建模型)
大家好,我是微学AI,今天给大家介绍一下计算机视觉的应用17-利用CrowdCountNet模型解决人群数量计算问题(pytorch搭建模型)。本篇文章,我将向大家展示如何使用CrowdCountNet这个神奇的工具,以及它是如何利用深度学习技术来解决复杂…...
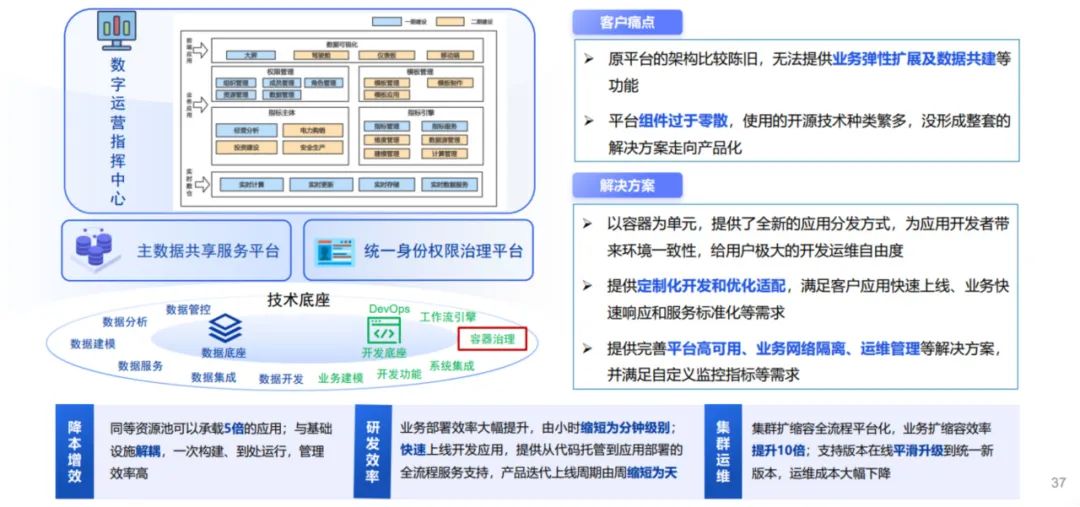
源启容器平台KubeGien 打造云原生转型的破浪之舰
云原生是应用上云的标准路径,也是未来发展大的趋势。如何将业务平滑过渡到云上?怎样应对上云期间的各项挑战呢?中电金信基于金融级数字底座“源启”打造了一款非常稳定可靠、多云异构、安全可控、开放灵活的容器平台产品——源启容器平台Kube…...

斯坦福机器学习 Lecture2 (假设函数、参数、样本等等术语,还有批量梯度下降法、随机梯度下降法 SGD 以及它们的相关推导,还有正态方程)
假设函数定义 假设函数,猜一个 x->y 的类型,比如 y ax b,随后监督学习的任务就是找到误差最低的 a 和 b 参数 有时候我们可以定义 x0 1,来让假设函数的整个表达式一致统一 如上图是机器学习中的一些术语 额外的符号…...

【腾讯云云上实验室-向量数据库】TAI时代的数据枢纽-向量数据库 VectorDB
一、向量数据库的发展历程和时代机遇 回顾向量数据库的发展历程: 2012年开始,深度神经网络的发展催生了向量数据库的发展;2015年至2016年,Google和微软发布了标志性的论文;2017年,Facebook开源了Faiss框架…...

SciencePlots——绘制论文中的图片
文章目录 安装一、风格二、1 资源 安装 # 安装最新版 pip install githttps://github.com/garrettj403/SciencePlots.git# 安装稳定版 pip install SciencePlots一、风格 简单好用的深度学习论文绘图专用工具包–Science Plot 二、 1 资源 论文绘图神器来了:一行…...

Linux云原生安全:零信任架构与机密计算
Linux云原生安全:零信任架构与机密计算 构建坚不可摧的云原生防御体系 引言:云原生安全的范式革命 随着云原生技术的普及,安全边界正在从传统的网络边界向工作负载内部转移。Gartner预测,到2025年,零信任架构将成为超…...

NLP学习路线图(二十三):长短期记忆网络(LSTM)
在自然语言处理(NLP)领域,我们时刻面临着处理序列数据的核心挑战。无论是理解句子的结构、分析文本的情感,还是实现语言的翻译,都需要模型能够捕捉词语之间依时序产生的复杂依赖关系。传统的神经网络结构在处理这种序列依赖时显得力不从心,而循环神经网络(RNN) 曾被视为…...

深入解析C++中的extern关键字:跨文件共享变量与函数的终极指南
🚀 C extern 关键字深度解析:跨文件编程的终极指南 📅 更新时间:2025年6月5日 🏷️ 标签:C | extern关键字 | 多文件编程 | 链接与声明 | 现代C 文章目录 前言🔥一、extern 是什么?&…...
相比,优缺点是什么?适用于哪些场景?)
Redis的发布订阅模式与专业的 MQ(如 Kafka, RabbitMQ)相比,优缺点是什么?适用于哪些场景?
Redis 的发布订阅(Pub/Sub)模式与专业的 MQ(Message Queue)如 Kafka、RabbitMQ 进行比较,核心的权衡点在于:简单与速度 vs. 可靠与功能。 下面我们详细展开对比。 Redis Pub/Sub 的核心特点 它是一个发后…...

基于Java+MySQL实现(GUI)客户管理系统
客户资料管理系统的设计与实现 第一章 需求分析 1.1 需求总体介绍 本项目为了方便维护客户信息为了方便维护客户信息,对客户进行统一管理,可以把所有客户信息录入系统,进行维护和统计功能。可通过文件的方式保存相关录入数据,对…...

安全突围:重塑内生安全体系:齐向东在2025年BCS大会的演讲
文章目录 前言第一部分:体系力量是突围之钥第一重困境是体系思想落地不畅。第二重困境是大小体系融合瓶颈。第三重困境是“小体系”运营梗阻。 第二部分:体系矛盾是突围之障一是数据孤岛的障碍。二是投入不足的障碍。三是新旧兼容难的障碍。 第三部分&am…...

Python Einops库:深度学习中的张量操作革命
Einops(爱因斯坦操作库)就像给张量操作戴上了一副"语义眼镜"——让你用人类能理解的方式告诉计算机如何操作多维数组。这个基于爱因斯坦求和约定的库,用类似自然语言的表达式替代了晦涩的API调用,彻底改变了深度学习工程…...

从 GreenPlum 到镜舟数据库:杭银消费金融湖仓一体转型实践
作者:吴岐诗,杭银消费金融大数据应用开发工程师 本文整理自杭银消费金融大数据应用开发工程师在StarRocks Summit Asia 2024的分享 引言:融合数据湖与数仓的创新之路 在数字金融时代,数据已成为金融机构的核心竞争力。杭银消费金…...

Python竞赛环境搭建全攻略
Python环境搭建竞赛技术文章大纲 竞赛背景与意义 竞赛的目的与价值Python在竞赛中的应用场景环境搭建对竞赛效率的影响 竞赛环境需求分析 常见竞赛类型(算法、数据分析、机器学习等)不同竞赛对Python版本及库的要求硬件与操作系统的兼容性问题 Pyth…...
