世界坐标系,相机坐标系,像素坐标系转换 详细说明(附代码)
几个坐标系介绍,相机内外参的回顾参考此文。
本文主要说明如何在几个坐标系之间转换。
本文涉及:
- 使用相机内参 在 像素坐标系 和 相机坐标系 之间转换。
- 使用相机外参(位姿)在相机坐标系 和 世界坐标系 之间转换。
- (qw,qx,qy,qz,tx,ty,tz)形式的外参如何使用。
- 以具体情景为例,每一步详细说明,并结合代码进一步理解每个步骤。
以下面的情景为例。
假设 I1 (img1) 上有一点p1,现在要通过相机1,相机2的内外参把p1映射到 I2 (img2)上的对应点p2.
还需要知道p1的深度,假设有img1的深度图,可以读取p1处的深度。
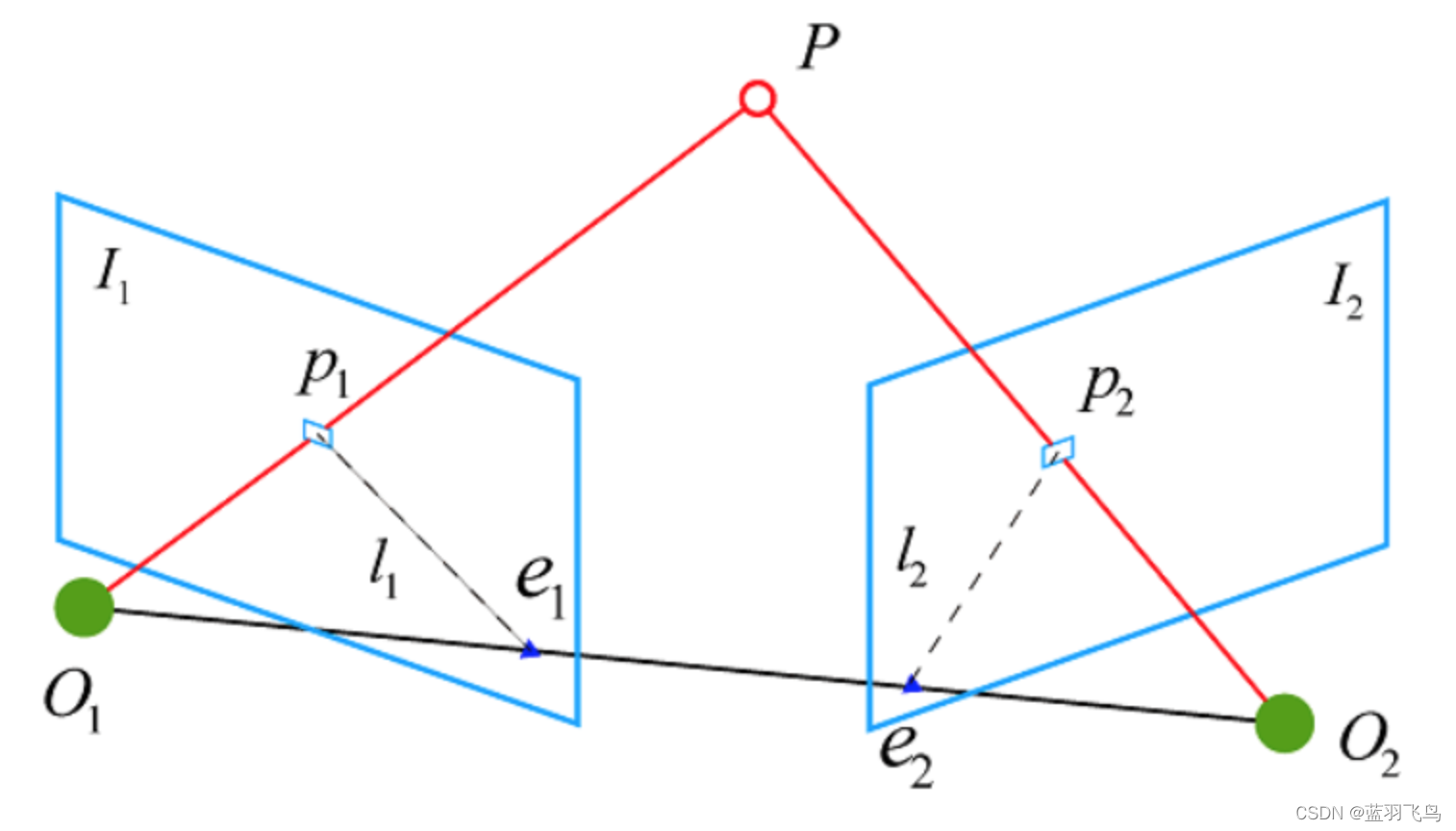
整体思路:
p1在图片 I1 上,是像素坐标系,根据camera1的内参把它转到camera1的相机坐标系,得到(xc1, yc1, zc1),
根据camera1的外参把 (xc1, yc1, zc1) 转到 世界坐标系,得到上图中的P点坐标(xw1, yw1, zw1),
根据camera2的外参把P点 (xw1, yw1, zw1) 转到camera2的相机坐标系,得到 (xc2, yc2, zc2).
最后根据camera2的内参 把 (xc2, yc2, zc2) 转到像素坐标系,得到图像 I2 上的 p2 点坐标(x2, y2).
整个坐标系的转换关系:像素1 -> 相机1 -> 世界 -> 相机2 -> 像素2
其中,像素坐标系为2D,其他都是3D。
相机外参 也 称为 位姿 (pose).
具体步骤:
(1). p1 像素坐标 --> 相机1 坐标
这两个坐标系的关系由相机内参决定,
相机内参(fx, fy, cx, cy)
假设像素坐标为(x1, y1), 相机1坐标为(xc1, yc1, zc1), 其中zc1为 I1 的深度图 (xc1, yc1)处的值,那么
x 1 = f x x c 1 z c 1 + c x x_{1} = f_{x}\frac{x_{c1}}{z_{c1}} + c_{x} x1=fxzc1xc1+cx, y 1 = f y y c 1 z c 1 + c y y_{1} = f_{y}\frac{y_{c1}}{z_{c1}} + c_{y} y1=fyzc1yc1+cy (1)
现在要求 xc1 和 yc1, 由(1)得到
x c 1 = ( x 1 − c x ) ∗ z c 1 / f x x_{c1} = (x_{1}- c_{x}) * z_{c1} / f_{x} xc1=(x1−cx)∗zc1/fx y c 1 = ( y 1 − c y ) ∗ z c 1 / f y y_{c1} = (y_{1}- c_{y}) * z_{c1} / f_{y} yc1=(y1−cy)∗zc1/fy
代码:
depth1_ori = cv2.imread("depth1.png", -1) #uint16型
depth1 = cv2.split(depth1_ori)[0]
#p1点对应的相机坐标
zc1 = depth1[y1, x1] / 1000.0 #这里深度单位是mm
xc1 = (x1 - cx) * zc1 / fx
yc1 = (y1 - cy) * zc1 / fy
(2). p1 的相机1 坐标 --> 世界坐标
转换关系: 相机坐标 = T * 世界坐标, 世界坐标 = T-1 * 相机坐标
其中 T 为world -> camera的转换矩阵。
如何求得转换矩阵 T ?先从概念介绍开始,
旋转矩阵R :3 * 3矩阵
平移向量 t : 3 * 1矩阵
把R 和 t 拼成转换矩阵 T :4 * 4矩阵,
T = [ R t 0 T 1 ] T = \begin{bmatrix} R & t\\ 0^{T}&1 \end{bmatrix} T=[R0Tt1]
顺便提一下李群李代数,T是SE(3), R是SO(3).
话题回到坐标,(xc1, yc1, zc1)为相机1坐标,(xw, yw, zw) 为世界坐标,那么世界坐标转相机坐标为:
[ x c 1 y c 1 z c 1 1 ] = T ⋅ [ x w y w z w 1 ] \begin{bmatrix} x_{c1} \\ y_{c1}\\ z_{c1}\\ 1 \end{bmatrix} = T \cdot \begin{bmatrix} x_{w} \\ y_{w}\\ z_{w}\\ 1 \end{bmatrix} xc1yc1zc11 =T⋅ xwywzw1
你肯定很好奇,为什么要加一维呢?
如果 T T T 不加最后一行的 [ 0 T 1 ] \begin{bmatrix} 0^{T}&1 \end{bmatrix} [0T1],坐标也不加最后一维的1,直接 T = [ R t ] T = \begin{bmatrix} R & t \end{bmatrix} T=[Rt] 也能计算,为什么一定要加一维?
[ x c y c z c ] = T ⋅ [ x w y w z w ] \begin{bmatrix} x_{c} \\ y_{c}\\ z_{c} \end{bmatrix} = T \cdot \begin{bmatrix} x_{w} \\ y_{w}\\ z_{w} \end{bmatrix} xcyczc =T⋅ xwywzw , 这里 T = [ R t ] T = \begin{bmatrix}R & t\end{bmatrix} T=[Rt]
是这样的,现在是从 世界坐标 转 相机1坐标 ,如果要把 相机1坐标 转 世界坐标 呢?
(我们现在要做的就是把 p1的 相机1坐标 转到 世界坐标。)
那就需要这么计算了,
[ x w y w z w ] = T − 1 ⋅ [ x c y c z c ] \begin{bmatrix} x_{w} \\ y_{w}\\ z_{w} \end{bmatrix} = T^{-1}\cdot \begin{bmatrix} x_{c} \\ y_{c}\\ z_{c} \end{bmatrix} xwywzw =T−1⋅ xcyczc ,这里 T = [ R t ] T = \begin{bmatrix}R & t\end{bmatrix} T=[Rt],无法求逆矩阵
求 T 的逆矩阵,T 必须是square(行数 = 列数)的,不能是3 * 4, 必须是4 * 4的。
所以加上一行,凑成 4 * 4 矩阵
T = [ R t 0 T 1 ] T = \begin{bmatrix} R & t\\ 0^{T}&1 \end{bmatrix} T=[R0Tt1]
那么 相机坐标 --> 世界坐标 就变为:
[ x w y w z w 1 ] = T − 1 ⋅ [ x c y c z c 1 ] \begin{bmatrix} x_{w} \\ y_{w}\\ z_{w}\\ 1 \end{bmatrix} = T^{-1} \cdot \begin{bmatrix} x_{c} \\ y_{c}\\ z_{c}\\ 1 \end{bmatrix} xwywzw1 =T−1⋅ xcyczc1
有的程序中会使用Twc, Tcw这样的称呼,这里w指world, 是世界坐标,c指camera, 是相机坐标。
T表示转换矩阵,至于Twc 是world转camera 还是camera转world, 需要根据实际情况而定(每个开发者习惯不一样)。
实际中,到了这里估计还是不知如何计算 T,问题在哪呢?
我们拿到的 相机外参 一般会是一个四元数+平移向量的形式,其中并没有R矩阵。
相机外参:(qw, qx, qy, qz, tx, ty, tz), (这个顺序要根据实际情况而定,有的相机顺序并不是这样)。
这里用四元数 q = (qw, qx, qy, qz) 代替了R矩阵,
原因在于R是3 * 3矩阵,有9个量,而一次旋转只有3个自由度,这种表达方式是冗余的,四元数的表达更紧凑。
上面是涉及到的相关概念,现在开始计算T。
计算转换矩阵 T
现在要先把 q 转为 R,再由R, t 得到T。
q = (qw, qx, qy, qz), (一定是qw, qx, qy ,qz的顺序,不是的先调整到这个顺序)
t = (tx, ty, tz), 这里要注意t 的单位,如果是mm, 需要 / 1000.0.
如果用Eigen库,可以这么得到T,
Isometry3d是4 * 4 欧式变换矩阵,就是T的格式(参考)
Eigen::Quaterniond q(qw, qx, qy, qz);
Eigen::Isometry3d T(q);
//先设置的旋转矩阵,下面平移要在旋转前的坐标系上平移,所以是pretranslate
T.pretranslate(Eigen::Vector3d(tx, ty, tz));
如果用Sophus::SE3d
SE3d T = SE3d(Quaterniond(qw, qx, qy, qz),Vector3d(tx, ty, tz)));
直接计算的话,由四元数 q 到旋转矩阵 R 的公式为(转此处的图):
这里q0, q1, q2, q3分别对应 qw, qx, qy, qz.
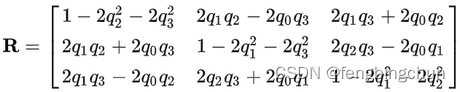
结合 (tx, ty, tz), 下面再加一行 [ 0 T 1 ] \begin{bmatrix} 0^{T}&1 \end{bmatrix} [0T1],得到T1 (由相机1的外参得到)。
T1 = np.array([[1 - 2 * q2 ** 2 - 2 * q3 ** 2,2 * q1 * q2 - 2 * q0 * q3,2 * q1 * q3 + 2 * q0 * q2,tx, #注意单位,如果是mm,要/1000.0],[2 * q1 * q2 + 2 * q0 * q3,1 - 2 * q1 ** 2 - 2 * q3 ** 2,2 * q2 * q3 - 2 * q0 * q1,ty, #注意单位,如果是mm,要/1000.0],[2 * q1 * q3 - 2 * q0 * q2,2 * q2 * q3 + 2 * q0 * q1,1 - 2 * q1 ** 2 - 2 * q2 ** 2,tz, #注意单位,如果是mm,要/1000.0],[0,0,0,1],])
已经得到了T1,下面可把相机坐标转为世界坐标
[ x w y w z w 1 ] = T 1 − 1 ⋅ [ x c 1 y c 1 z c 1 1 ] \begin{bmatrix} x_{w} \\ y_{w}\\ z_{w}\\ 1 \end{bmatrix} = T_{1}^{-1} \cdot \begin{bmatrix} x_{c1} \\ y_{c1}\\ z_{c1}\\ 1 \end{bmatrix} xwywzw1 =T1−1⋅ xc1yc1zc11
代码:
p1_c = np.array([xc1, yc1, zc1, 1])
p_w = np.matmul(np.linalg.inv(T1), np.expand_dims(p1_c,1))
(3). 世界坐标 --> 相机2坐标
上面已经说明了如何由 世界坐标 转 相机坐标。
注意上面求的T1 是由相机1的外参得到,
这里要用到相机2的外参,camera2: (qw2, qx2, qy2, qz2, tx2, ty2, tz2),
求得T2 后,由下式得到 P 的相机2坐标
[ x c 2 y c 2 z c 2 1 ] = T 2 ⋅ [ x w y w z w 1 ] \begin{bmatrix} x_{c2} \\ y_{c2}\\ z_{c2}\\ 1 \end{bmatrix} = T_{2} \cdot \begin{bmatrix} x_{w} \\ y_{w}\\ z_{w}\\ 1 \end{bmatrix} xc2yc2zc21 =T2⋅ xwywzw1
p2_c = np.matmul(T2, p_w)
(4) 相机2坐标 --> 像素坐标2
相机内参(fx, fy, cx, cy)
x 2 = f x x c 2 z c 2 + c x x_{2} = f_{x}\frac{x_{c2}}{z_{c2}} + c_{x} x2=fxzc2xc2+cx, y 2 = f y y c 2 z c 2 + c y y_{2} = f_{y}\frac{y_{c2}}{z_{c2}} + c_{y} y2=fyzc2yc2+cy
xc2 = p2_c[0]
yc2 = p2_c[1]
zc2 = p2_c[2]
x2 = xc2 * fx / zc2 + cx
y2 = yc2 * fy / zc2 + cy
这样就得到了图像 I2 上的映射点 p2的坐标。
相关文章:
世界坐标系,相机坐标系,像素坐标系转换 详细说明(附代码)
几个坐标系介绍,相机内外参的回顾参考此文。 本文主要说明如何在几个坐标系之间转换。 本文涉及: 使用相机内参 在 像素坐标系 和 相机坐标系 之间转换。使用相机外参(位姿)在相机坐标系 和 世界坐标系 之间转换。(qw,qx,qy,qz,…...
计算机毕业设计 基于SpringBoot的企业内部网络管理系统的设计与实现 Java实战项目 附源码+文档+视频讲解
博主介绍:✌从事软件开发10年之余,专注于Java技术领域、Python人工智能及数据挖掘、小程序项目开发和Android项目开发等。CSDN、掘金、华为云、InfoQ、阿里云等平台优质作者✌ 🍅文末获取源码联系🍅 👇🏻 精…...
)
CISP模拟试题(三)
免责声明 文章仅做经验分享用途,利用本文章所提供的信息而造成的任何直接或者间接的后果及损失,均由使用者本人负责,作者不为此承担任何责任,一旦造成后果请自行承担!!! 1. 人们对信息安全的认识从信息技术安全发展到信息安全保障,主要是由于: A.为了更好地完成组…...

前端调取摄像头并实现拍照功能
前言 最近接到的一个需求十分有意思,设计整体实现了前端仿 微信扫一扫 的功能。整理了一下思路,做一个分享。 tips: 如果想要实现完整扫一扫的功能,你需要掌握一些前置知识,这次我们先讲如何实现拍照并且保存的功能。 一. wind…...

android —— 阴影效果和跑马灯效果Textview
1、带阴影的TextView ①、 android:shadowColor“color/black” 设置阴影颜色,需要与shadowRadius一起使用 ②、android:shadowRadius“3.0” 设置阴影模糊程度,设为0.1会变成字体颜色,建议设置3.0 ③、android:shadowDx“10” 设置阴影在水…...
多态语法详解
多态语法详解 一:概念1:多态实现条件 二:重写:三:向上转型和向下转型1:向上转型:1:直接赋值:2:方法传参3:返回值 2:向下转型 一:概念 1:同一个引…...

Python大数据之linux学习总结——day11_ZooKeeper
ZooKeeper ZK概述 ZooKeeper概念: Zookeeper是一个分布式协调服务的开源框架。本质上是一个分布式的小文件存储系统 ZooKeeper作用: 主要用来解决分布式集群中应用系统的一致性问题。 ZooKeeper结构: 采用树形层次结构,ZooKeeper树中的每个节点被称为—Znode。且树…...
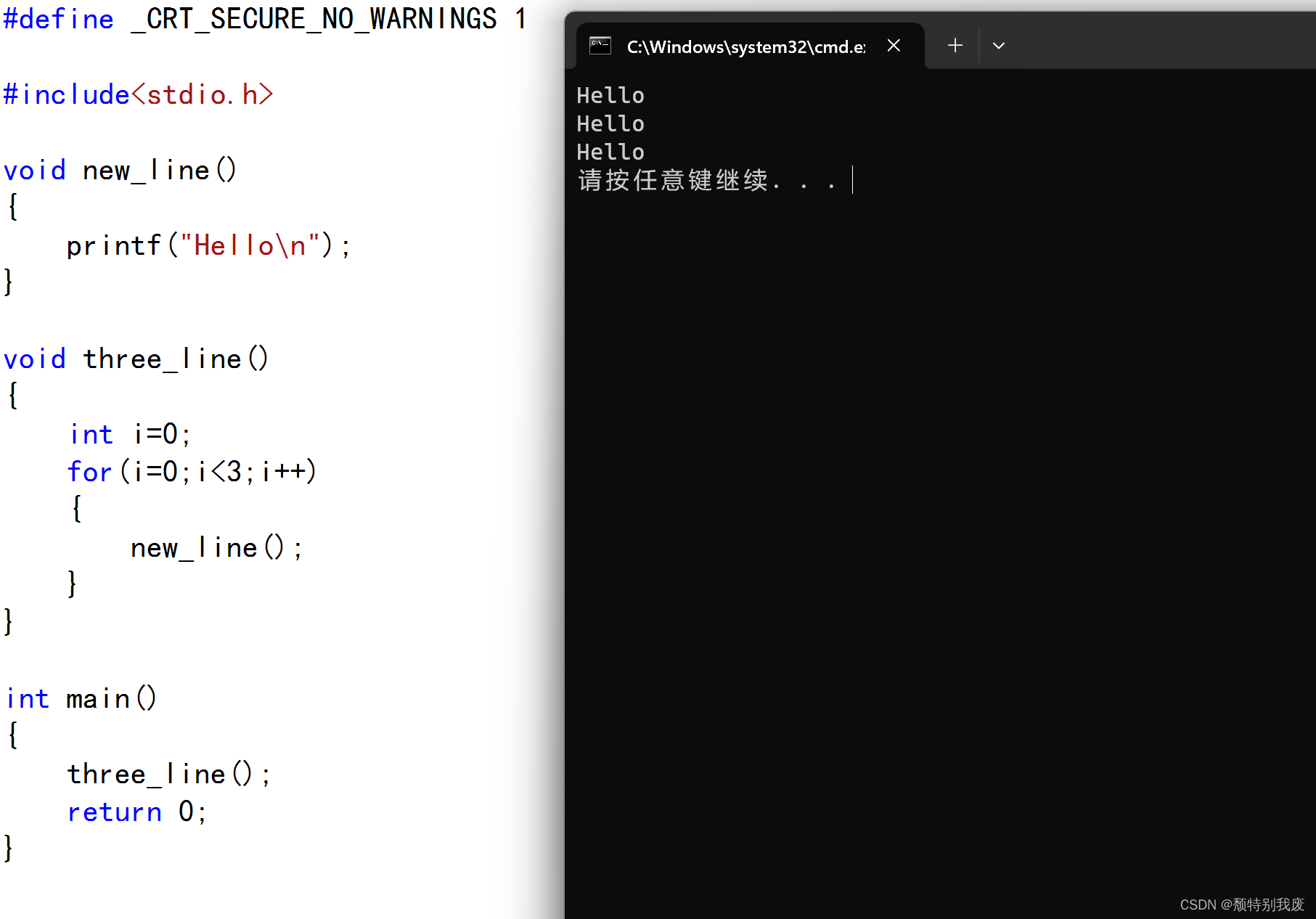
C语言——函数的嵌套调用
#define _CRT_SECURE_NO_WARNINGS 1#include<stdio.h>void new_line() {printf("Hello\n"); }void three_line() {int i0;for(i0;i<3;i){new_line();} }int main() {three_line();return 0; }...
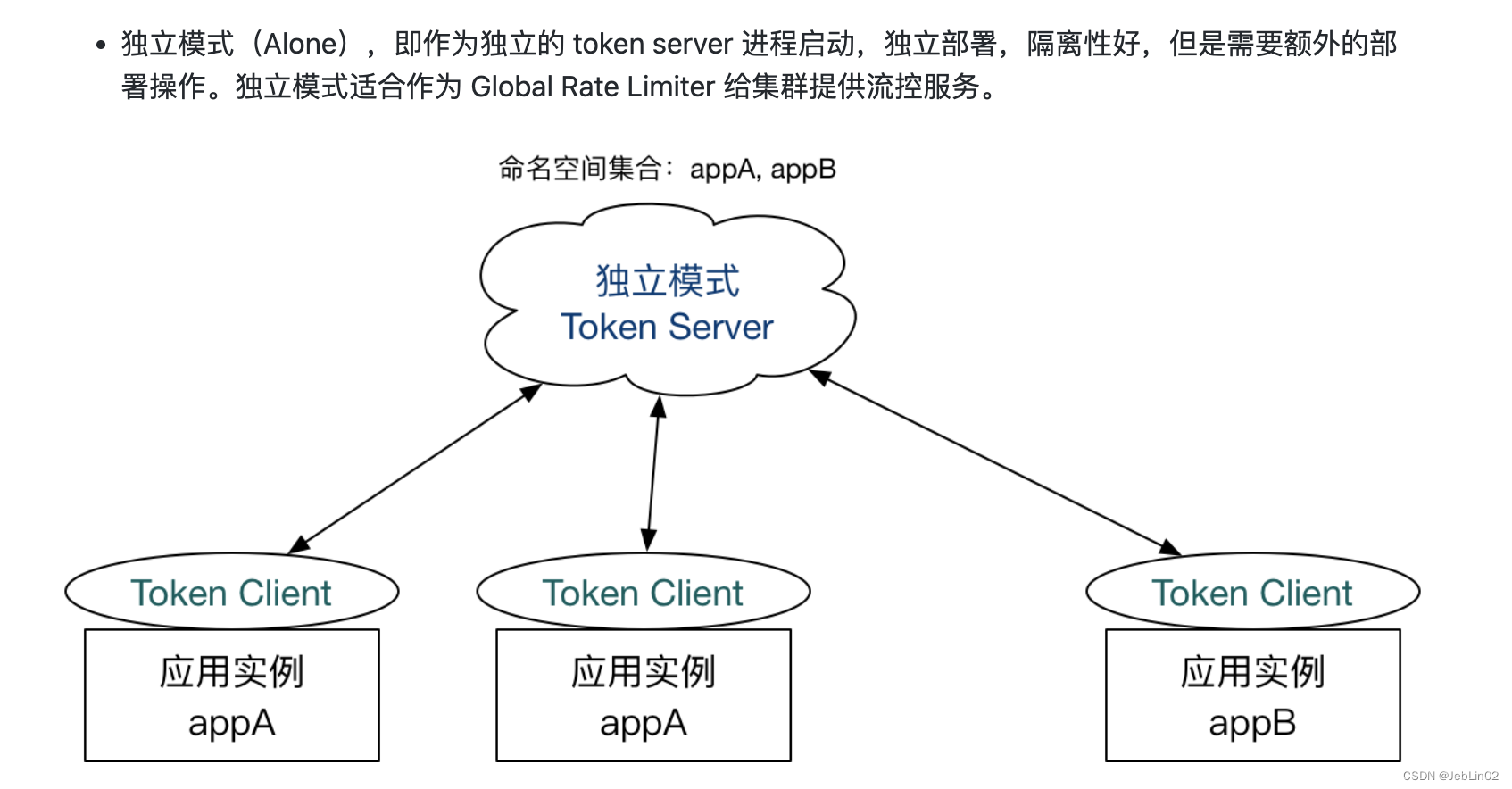
4种经典的限流算法与集群限流
0、基础知识 1000毫秒内,允许2个请求,其他请求全部拒绝。 不拒绝就可能往db打请求,把db干爆~ interval 1000 rate 2; 一、固定窗口限流 固定窗口限流算法(Fixed Window Rate Limiting Algorithm)是…...

网工内推 | 国企、港企网工,年底双薪,NA以上认证即可
01 中航期货有限公司 招聘岗位:信息技术部-网络工程师 职责描述: 1、负责总部、分支机构、外联单位网络的日常运维、故障和应急处置,特别是定期监测设备的运行状态,对存在隐患的地方及时发现改正,保持网络稳定通畅&am…...

【华为HCIP | 华为数通工程师】刷题日记1116(一个字惨)
个人名片: 🐼作者简介:一名大三在校生,喜欢AI编程🎋 🐻❄️个人主页🥇:落798. 🐼个人WeChat:hmmwx53 🕊️系列专栏:🖼️…...
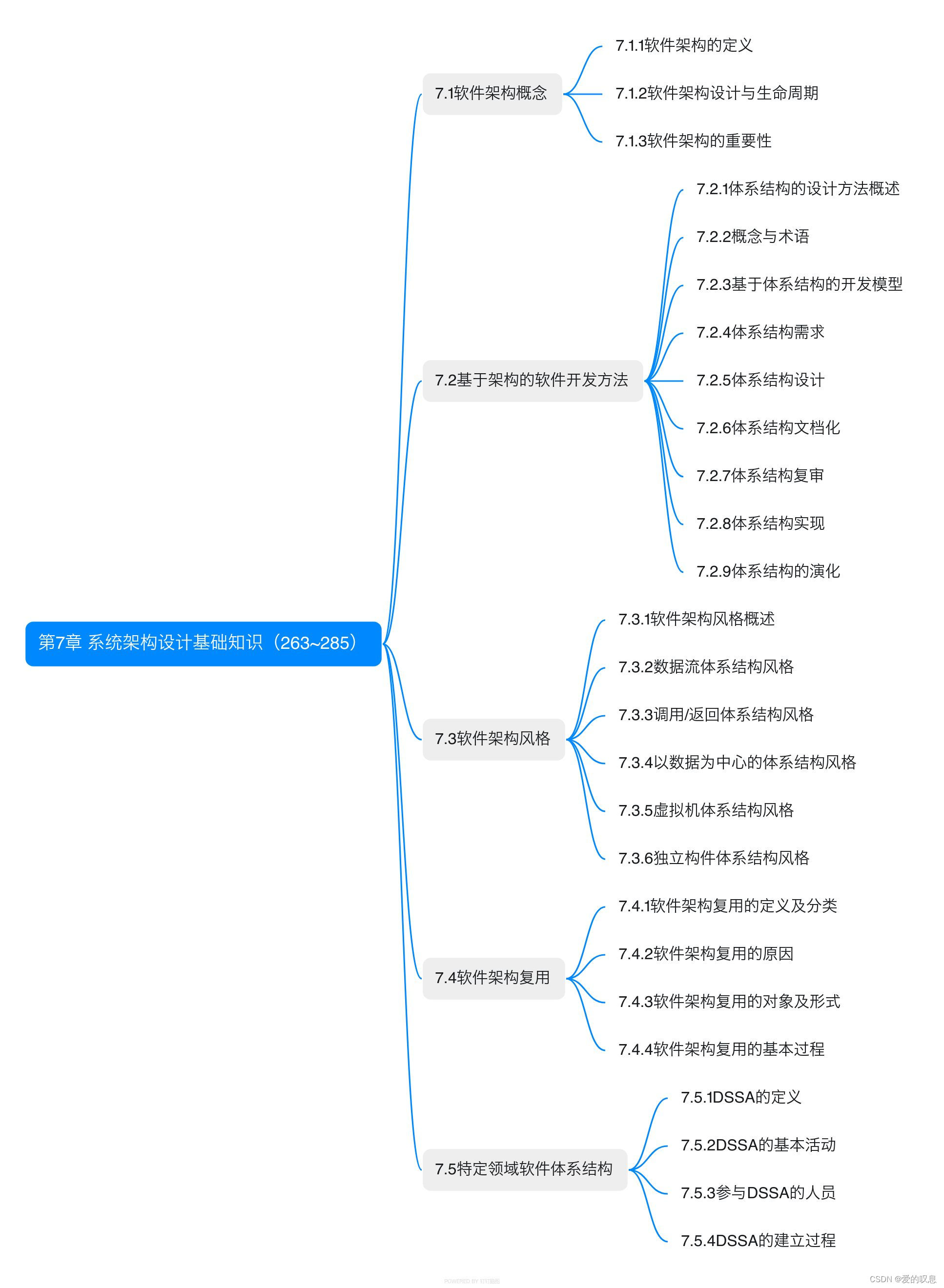
软考-高级-系统架构设计师教程(清华第2版)【第7章 系统架构设计基础知识(263~285)-思维导图】
软考-高级-系统架构设计师教程(清华第2版)【第7章 系统架构设计基础知识(263~285)-思维导图】 课本里章节里所有蓝色字体的思维导图...

⑩⑥ 【MySQL】详解 触发器TRIGGER,协助 确保数据的完整性,日志记录,数据校验等操作。
个人简介:Java领域新星创作者;阿里云技术博主、星级博主、专家博主;正在Java学习的路上摸爬滚打,记录学习的过程~ 个人主页:.29.的博客 学习社区:进去逛一逛~ 触发器 ⑩⑥ 【MySQL】触发器详解1. 什么是触发…...
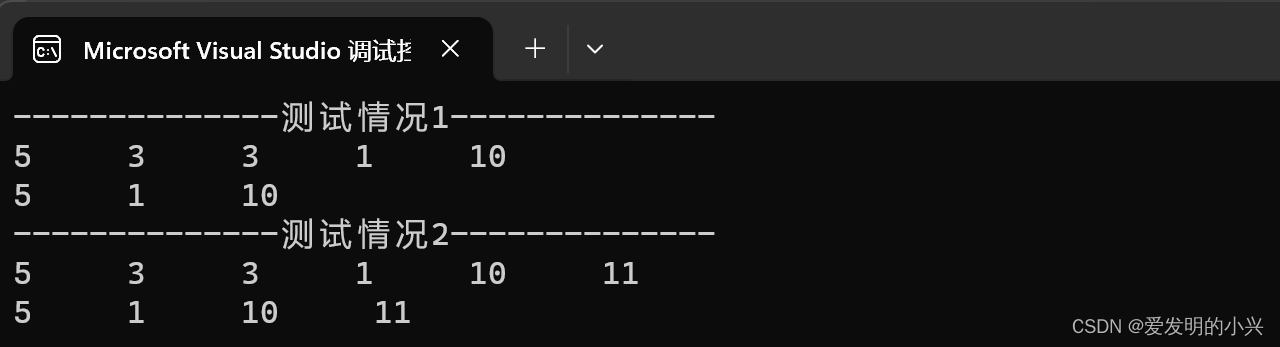
数据结构与算法编程题3
长度为n的顺序表,删除线性表所有值为x的元素,使得时间复杂度为O(n),空间复杂度为O(1) #include <iostream> using namespace std;typedef int ElemType; #define Maxsize 100 #define OK 1 #define ERROR 0 typedef struct SqList {E…...
)
Go基础面经大全(持续补充中)
Go基础 1. 基础特性 Go的优势 天生支持并发,性能高。 单一的标准代码格式,比其他语言更具可读性。 自动垃圾收集机制比Java和Python更有效,因为它与程序同时执行。 Go数据类型 int, string, float, bool, array, slice, map, channel, p…...

uniapp heckbox-group实现多选
文章目录 html 代码JS 代码 混了业务逻辑,谨慎观看 html 代码 <view><!--可滚动视图区域。用于区域滚动 --><scroll-view :style"{ height: clientHeight px }" :scroll-top"scrollTop" scroll-y"true"scrolltouppe…...
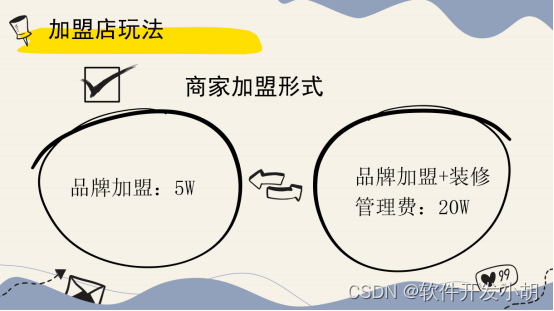
读懂:“消费报销”模式新零售打法,适用连锁门店加盟的营销方案
读懂:“消费报销”模式新零售打法,适用连锁门店加盟的营销方案 引言:2023年的双十一已经落下帷幕,作为每年的经典电商促销节,今年已是第15个年头,但是今年各大电商平台却都是非常默契的,没有公布…...

一个基本的http客户端
高可用 客户端 1. httpClient.h #include <iostream> #include <string> #include <functional>class HttpClient { public:HttpClient(std::string url) : url_(url), port_(0) {}int write_http(const std::string &method, const std::string &…...

html-网站菜单-点击菜单展开相应的导航栏,加减号可切换
一、效果图 1.点击显示菜单栏,点击x号关闭; 2.点击一级菜单,展开显示二级,并且加号变为减号; 3.点击其他一级导航,自动收起展开的导航。 二、代码实现 <!DOCTYPE html> <html><head>&…...
2.FastRunner定时任务Celery+RabbitMQ
注意:celery版本和Python冲突问题 不能用高版本Python 用3.5以下,因为项目的celery用的django-celery 3.2.2 python3.7 async关键字 冲突版本 celery3.x方案一: celery3.xpython3.6方案二 : celery4.xpython3.7 解决celery执…...

从WWDC看苹果产品发展的规律
WWDC 是苹果公司一年一度面向全球开发者的盛会,其主题演讲展现了苹果在产品设计、技术路线、用户体验和生态系统构建上的核心理念与演进脉络。我们借助 ChatGPT Deep Research 工具,对过去十年 WWDC 主题演讲内容进行了系统化分析,形成了这份…...

练习(含atoi的模拟实现,自定义类型等练习)
一、结构体大小的计算及位段 (结构体大小计算及位段 详解请看:自定义类型:结构体进阶-CSDN博客) 1.在32位系统环境,编译选项为4字节对齐,那么sizeof(A)和sizeof(B)是多少? #pragma pack(4)st…...

FastAPI 教程:从入门到实践
FastAPI 是一个现代、快速(高性能)的 Web 框架,用于构建 API,支持 Python 3.6。它基于标准 Python 类型提示,易于学习且功能强大。以下是一个完整的 FastAPI 入门教程,涵盖从环境搭建到创建并运行一个简单的…...

Opencv中的addweighted函数
一.addweighted函数作用 addweighted()是OpenCV库中用于图像处理的函数,主要功能是将两个输入图像(尺寸和类型相同)按照指定的权重进行加权叠加(图像融合),并添加一个标量值&#x…...

MODBUS TCP转CANopen 技术赋能高效协同作业
在现代工业自动化领域,MODBUS TCP和CANopen两种通讯协议因其稳定性和高效性被广泛应用于各种设备和系统中。而随着科技的不断进步,这两种通讯协议也正在被逐步融合,形成了一种新型的通讯方式——开疆智能MODBUS TCP转CANopen网关KJ-TCPC-CANP…...
)
python爬虫:Newspaper3k 的详细使用(好用的新闻网站文章抓取和解析的Python库)
更多内容请见: 爬虫和逆向教程-专栏介绍和目录 文章目录 一、Newspaper3k 概述1.1 Newspaper3k 介绍1.2 主要功能1.3 典型应用场景1.4 安装二、基本用法2.2 提取单篇文章的内容2.2 处理多篇文档三、高级选项3.1 自定义配置3.2 分析文章情感四、实战案例4.1 构建新闻摘要聚合器…...

TRS收益互换:跨境资本流动的金融创新工具与系统化解决方案
一、TRS收益互换的本质与业务逻辑 (一)概念解析 TRS(Total Return Swap)收益互换是一种金融衍生工具,指交易双方约定在未来一定期限内,基于特定资产或指数的表现进行现金流交换的协议。其核心特征包括&am…...

HBuilderX安装(uni-app和小程序开发)
下载HBuilderX 访问官方网站:https://www.dcloud.io/hbuilderx.html 根据您的操作系统选择合适版本: Windows版(推荐下载标准版) Windows系统安装步骤 运行安装程序: 双击下载的.exe安装文件 如果出现安全提示&…...

LLM基础1_语言模型如何处理文本
基于GitHub项目:https://github.com/datawhalechina/llms-from-scratch-cn 工具介绍 tiktoken:OpenAI开发的专业"分词器" torch:Facebook开发的强力计算引擎,相当于超级计算器 理解词嵌入:给词语画"…...

Map相关知识
数据结构 二叉树 二叉树,顾名思义,每个节点最多有两个“叉”,也就是两个子节点,分别是左子 节点和右子节点。不过,二叉树并不要求每个节点都有两个子节点,有的节点只 有左子节点,有的节点只有…...
