【python】直方图正则化详解和示例
直方图正则化(Histogram Normalization)是一种图像增强技术,目的是改变图像的直方图以改善图像的质量。具体来说,它通过将图像的直方图调整为指定的形状,以增强图像的对比度和亮度。
直方图正则化的基本步骤如下:
计算输入图像的直方图和累积分布函数(CDF)。
计算正则化的直方图,使其具有相同的CDF。
使用正则化的直方图来映射输入图像的像素值。
下面是一个使用Python和OpenCV库实现直方图正则化的示例代码:
import cv2
import numpy as np
import matplotlib.pyplot as plt# 加载图像
image = cv2.imread('11111.jpg', cv2.IMREAD_GRAYSCALE)# 计算输入图像的直方图和累积分布函数(CDF)
hist, bins = np.histogram(image.flatten(), 256, [0, 256])
cdf = hist.cumsum()
cdf_normalized = cdf * hist.max() / cdf.max()# 计算正则化的直方图
cdf_m = np.ma.masked_equal(cdf, 0)
cdf_m = (cdf_m - cdf_m.min()) * 255 / (cdf_m.max() - cdf_m.min())
cdf_final = (cdf_m - cdf_m.min()) * hist.max() / (cdf_m.max() - cdf_m.min())# 使用正则化的直方图来映射输入图像的像素值
image_normalized = np.interp(image.flatten(), bins[:-1], cdf_final)
image_normalized = image_normalized.reshape(image.shape)# 显示原始图像、正则化后的图像和直方图
plt.subplot(2, 2, 1)
plt.imshow(image, cmap='gray')
plt.title('Original Image')
plt.xticks([]), plt.yticks([])plt.subplot(2, 2, 2)
plt.hist(image.flatten(), 256, [0, 256])
plt.title('Original Histogram')
plt.xlabel('Pixel Value')
plt.ylabel('Frequency')plt.subplot(2, 2, 3)
plt.imshow(image_normalized, cmap='gray')
plt.title('Normalized Image')
plt.xticks([]), plt.yticks([])plt.subplot(2, 2, 4)
plt.hist(image_normalized.flatten(), 256, [0, 256])
plt.title('Normalized Histogram')
plt.xlabel('Pixel Value')
plt.ylabel('Frequency')#plt.show()
plt.savefig("11111gray.jpg")
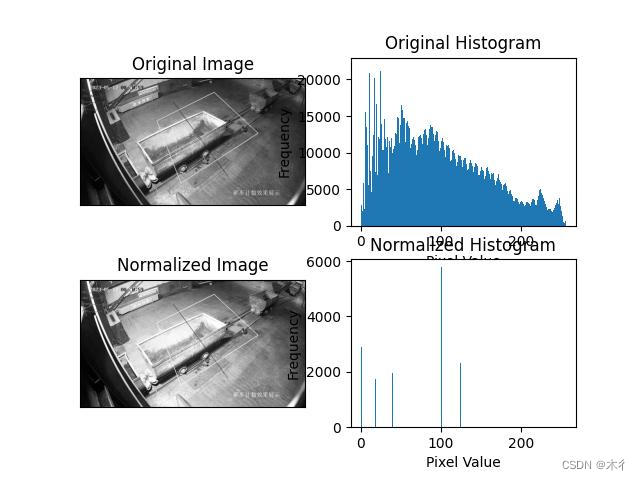
这段代码首先加载一张灰度图像,并计算其直方图和CDF。然后,它计算正则化的直方图,并使用该直方图来映射输入图像的像素值。最后,它显示原始图像、正则化后的图像和两个直方图。
效果图如下所示:
相关文章:

【python】直方图正则化详解和示例
直方图正则化(Histogram Normalization)是一种图像增强技术,目的是改变图像的直方图以改善图像的质量。具体来说,它通过将图像的直方图调整为指定的形状,以增强图像的对比度和亮度。 直方图正则化的基本步骤如下&…...

c语言:矩阵交换
题目: 代码和思路: #define _CRT_SECURE_NO_WARNINGS #include<stdio.h>int main() {int n 0;int m 0;int arr[10][10] { 0 }; // 输入行和列scanf("%d%d", &n, &m);int i 0;int j 0;//读取数组for (i 0; i < n; i)…...
【论文阅读】基于隐蔽带宽的汽车控制网络鲁棒认证(一)
文章目录 Abstract第一章 引言1.1 问题陈述1.2 研究假设1.3 贡献1.4 大纲 第二章 背景和相关工作2.1 CAN安全威胁2.1.1 CAN协议设计2.1.2 CAN网络攻击2.1.3 CAN应用攻击 2.2 可信执行2.2.1 软件认证2.2.2 消息身份认证2.2.3 可信执行环境2.2.4 Sancus2.2.5 VulCAN 2.3 侧信道攻…...

暖阳脚本_ 将Agent技术的灵活性引入RPA,清华等发布自动化智能体ProAgent
RPA暖阳脚本 近日,来自清华大学的研究人员联合面壁智能、中国人民大学、MIT、CMU 等机构共同发布了新一代流程自动化范式 “智能体流程自动化” Agentic Process Automation(APA),结合大模型智能体帮助人类进行工作流构建&#x…...
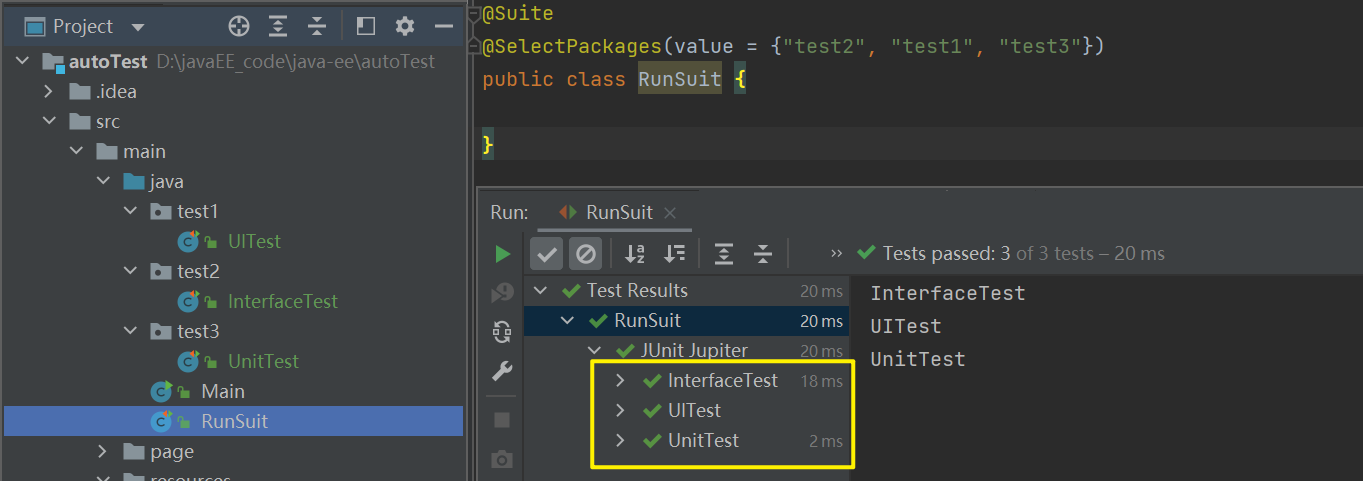
JUnit 单元自动化
一、Junit 是什么? Junit 是 Java 中用于单元测试的框架。使用 Junit 能让我们快速高效的完成单元测试。 自动化测试:JUnit提供了自动化测试的能力,开发人员可以编写一次测试用例,然后通过简单的命令或集成到持续集成工具中进行…...
——插槽 slot)
Vue3 源码解读系列(十一)——插槽 slot
slot 插槽的实现实际上就是一种 延时渲染,把父组件中编写的插槽内容保存到一个对象上,并且把具体渲染 DOM 的代码用函数的方式封装,然后在子组件渲染的时候,根据插槽名在对象中找到对应的函数,然后执行这些函数做真正的…...

[github初学者教程] 分支管理-以及问题解决
作者:20岁爱吃必胜客(坤制作人),近十年开发经验, 跨域学习者,目前于新西兰奥克兰大学攻读IT硕士学位。荣誉:阿里云博客专家认证、腾讯开发者社区优质创作者,在CTF省赛校赛多次取得好成绩。跨领域…...

见面礼——图论
给定一个 n 个点 n 条边的无向图,你需要求有多少种选择图上的一个点 p 和一条边 (x,y) 的方案,使得删去 (x,y) 后图变成一棵树,且这棵树以 p 为根时每个节点的儿子个数均不超过 3。保证至少存在一种这样的方案。 Input 输入的第一行一个整数…...

【论文阅读】SPARK:针对视觉跟踪的空间感知在线增量攻击
SPARK: Spatial-Aware Online Incremental Attack Against Visual Tracking introduction 在本文中,我们确定了视觉跟踪对抗性攻击的一个新任务:在线生成难以察觉的扰动,误导跟踪器沿着不正确的(无目标攻击,UA&#x…...

MR混合现实教学系统在汽车检修与维护课堂教学中的应用
传统的汽车检修与维护课堂教学主要依赖教师口头讲解和黑板演示,这种方式存在一定的局限性。首先,对于一些复杂的机械结构和操作过程,教师难以生动形象地展示给学生。其次,学生无法直接观察到实际操作中的细节和注意事项࿰…...

CentOS7安装xvfb,解决服务器没有X-Server的问题
Linux服务器上一般没有图形界面,但是有时候有些软件又需要图形界面.比如oracle,自动化测试(puppeteer).运行的时候会提示没有没有X服务. 这时候一般不会去特地装图形界面.这个时候就要用xvfb来创建虚拟图形窗口. xvfb介绍 Xvfb(X Virtual Frame Buffer)是基于X Window的虚拟服…...
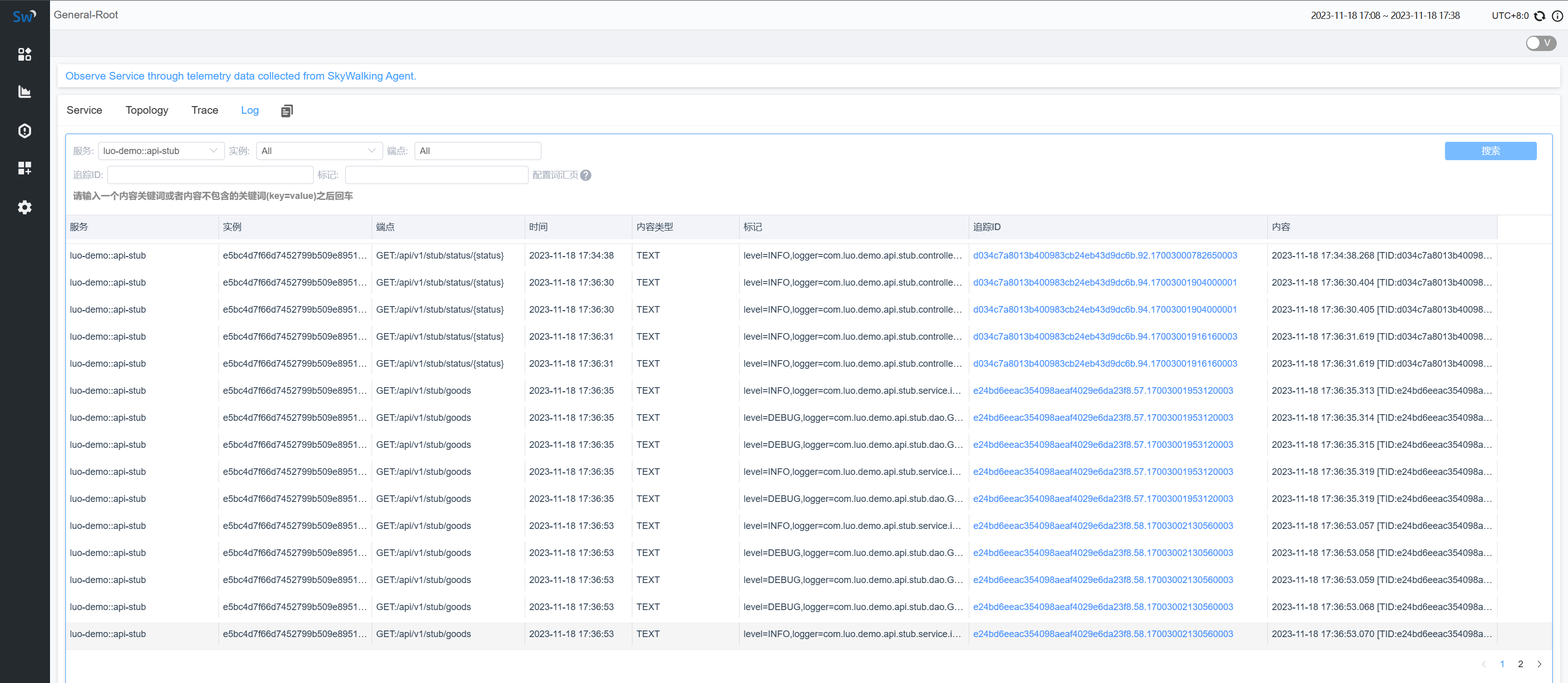
快速集成Skywalking 9(Windows系统、JavaAgent、Logback)
目录 一、Skywalking简介二、下载Skywalking服务端三、安装Skywalking服务端3.1 解压安装包3.2 启动Skywalking 四、关于Skywalking服务端更多配置五、Java应用集成skywalking-agent.jar5.1 下载SkyWalking Java Agent5.2 集成JavaAgent5.3 Logback集成Skywalking5.4 集成效果 …...

起立科技(起鸿)在第25届高交会上展示透明OLED技术创新
第二十五届中国国际高新技术成果交易会 日期:2023年11月15日 地点:福田会展中心7号馆 深圳,2023年11月15日 — 起鸿科技,作为透明OLED领域的引领者,于今日参展了第二十五届中国国际高新技术成果交易会。这一展会将汇…...

大模型LLM 在线量化;GPTQ\AWQ量化
1、大模型LLM 在线量化 参考:https://www.cnblogs.com/bruceleely/p/17348782.html ##8bit model = AutoModel.from_pretrained("THUDM/chatglm-6b", trust_remote_code=True).quantize(8).half(...

记一次线上bug排查-----SpringCloud Gateway组件 请求头accept-encoding导致响应结果乱码
基于公司的业务需求,在SpringCloud Gateway组件的基础上,写了一个转发服务,测试开发阶段运行正常,并实现初步使用。但三个月后,PostMan请求接口,返回异常,经排查,从日志中获取到转发…...
复杂数据统计与R语言程序设计实验一
1.下载并安装R语言软件,熟悉基本操作的命令及操作界面,掌握软件的使用方法(提供学号加姓名的截图)。 2.下载并安装Rstudio, (提供运行代码及运行结果的截图)。 3.下载并安装R包DT,…...

UEFI实战——键盘操作
一、键盘操作 UEFI下如何获取键盘键值,用户输入按键方式分两种:一种是单个按键,另外一种是组合按键。两种方式对应两个Protocol服务,接下来分步讲解。 二、单个按键 单个按键使用Protocol服务是EFI_SIMPLE_TEXT_INPUT_PROTOCOL,它定义在MdePkg/Include/Protocol/Simple…...
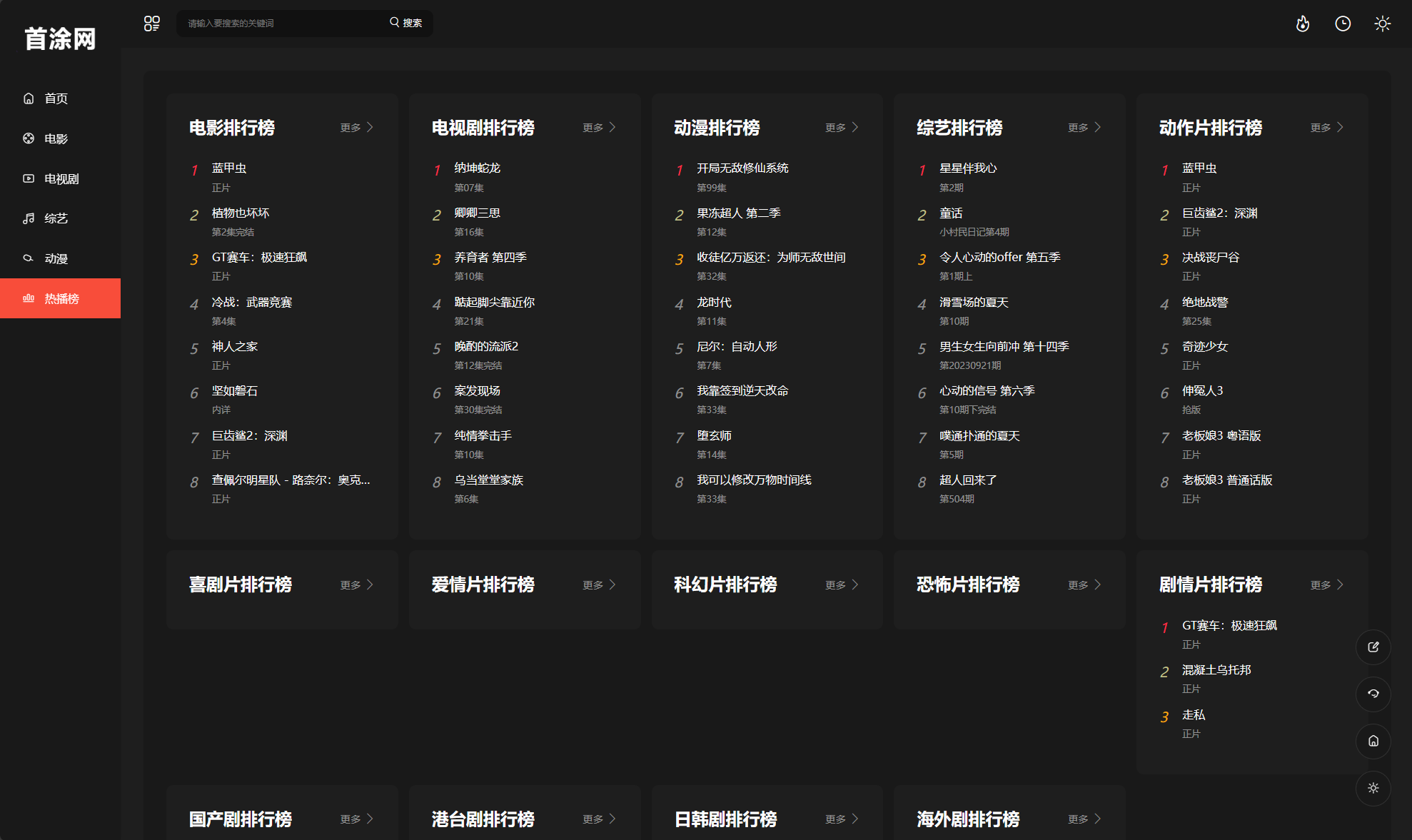
苹果CMS首涂第30套可装修DIY主题模板免授权版
这是一款可以装修的主题,类似淘宝店装修一样,可以针对首页、栏目页、详情页、播放页进行自定义装修,内置10个模块自由选择、添加、修改、删除、排序操作,后续升级还会增加更多实用和个性模块供选择,主题内包含的导航、…...

C#每天复习一个重要小知识day2:有参与无参构造函数
using System;public class MyClass {private int value;// 有参构造函数public MyClass(int v){this.value v;}// 无参构造函数public MyClass(){this.value 0;}public static void Main(string[] args){// 使用有参构造函数实例化对象MyClass obj1 new MyClass(10);Consol…...
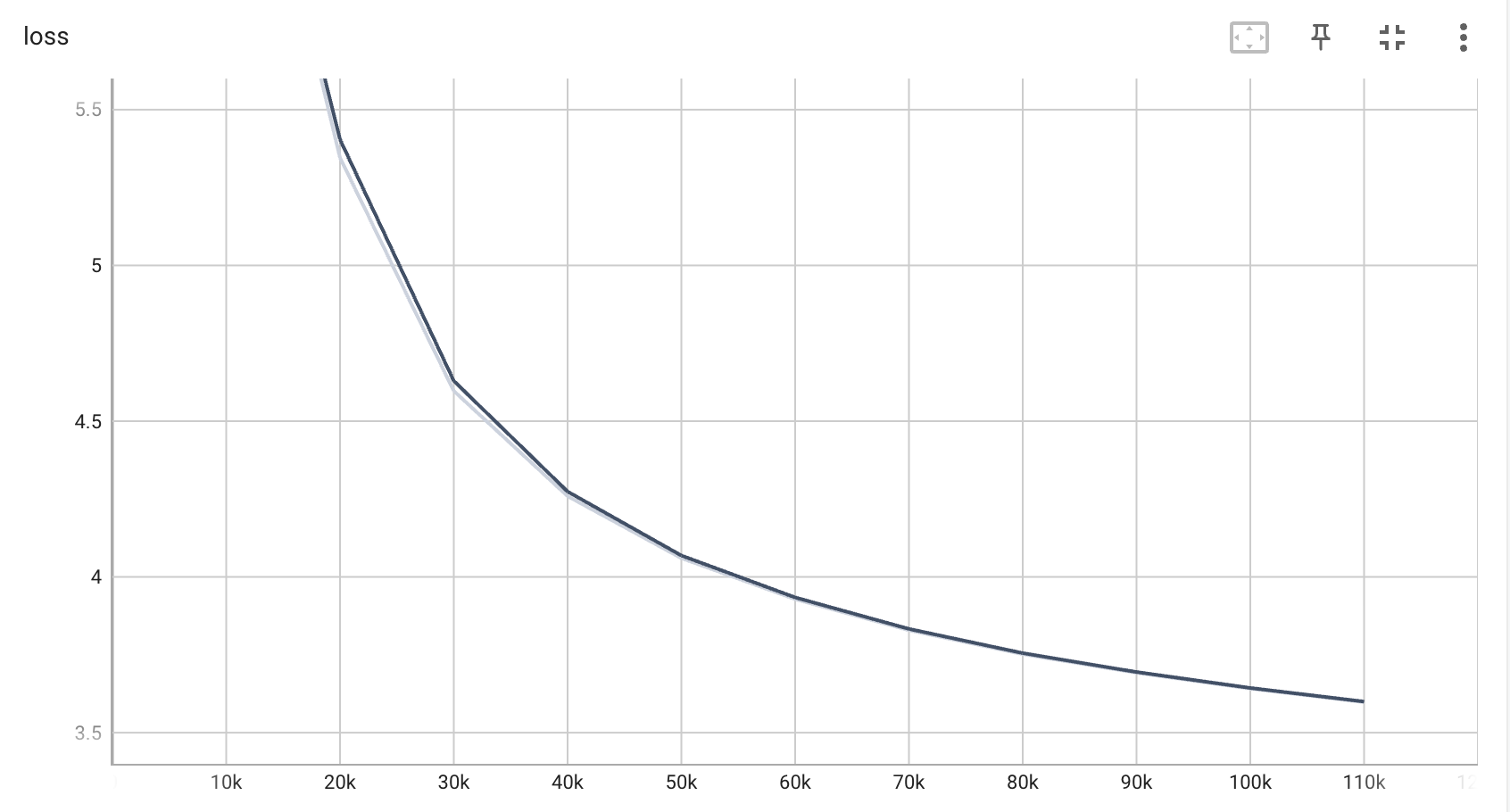
大语言模型的三阶段训练
为了训练专有领域模型,选择LLaMA2-7B作为基座模型,由于LLaMA模型中文词表有限,因此首先进行中文词表的扩展,然后进行三阶段训练(增量预训练,有监督微调,强化学习)。 代码将全部上传…...

阿里云ACP云计算备考笔记 (5)——弹性伸缩
目录 第一章 概述 第二章 弹性伸缩简介 1、弹性伸缩 2、垂直伸缩 3、优势 4、应用场景 ① 无规律的业务量波动 ② 有规律的业务量波动 ③ 无明显业务量波动 ④ 混合型业务 ⑤ 消息通知 ⑥ 生命周期挂钩 ⑦ 自定义方式 ⑧ 滚的升级 5、使用限制 第三章 主要定义 …...

dedecms 织梦自定义表单留言增加ajax验证码功能
增加ajax功能模块,用户不点击提交按钮,只要输入框失去焦点,就会提前提示验证码是否正确。 一,模板上增加验证码 <input name"vdcode"id"vdcode" placeholder"请输入验证码" type"text&quo…...

高等数学(下)题型笔记(八)空间解析几何与向量代数
目录 0 前言 1 向量的点乘 1.1 基本公式 1.2 例题 2 向量的叉乘 2.1 基础知识 2.2 例题 3 空间平面方程 3.1 基础知识 3.2 例题 4 空间直线方程 4.1 基础知识 4.2 例题 5 旋转曲面及其方程 5.1 基础知识 5.2 例题 6 空间曲面的法线与切平面 6.1 基础知识 6.2…...

令牌桶 滑动窗口->限流 分布式信号量->限并发的原理 lua脚本分析介绍
文章目录 前言限流限制并发的实际理解限流令牌桶代码实现结果分析令牌桶lua的模拟实现原理总结: 滑动窗口代码实现结果分析lua脚本原理解析 限并发分布式信号量代码实现结果分析lua脚本实现原理 双注解去实现限流 并发结果分析: 实际业务去理解体会统一注…...

初学 pytest 记录
安装 pip install pytest用例可以是函数也可以是类中的方法 def test_func():print()class TestAdd: # def __init__(self): 在 pytest 中不可以使用__init__方法 # self.cc 12345 pytest.mark.api def test_str(self):res add(1, 2)assert res 12def test_int(self):r…...

在QWebEngineView上实现鼠标、触摸等事件捕获的解决方案
这个问题我看其他博主也写了,要么要会员、要么写的乱七八糟。这里我整理一下,把问题说清楚并且给出代码,拿去用就行,照着葫芦画瓢。 问题 在继承QWebEngineView后,重写mousePressEvent或event函数无法捕获鼠标按下事…...

PAN/FPN
import torch import torch.nn as nn import torch.nn.functional as F import mathclass LowResQueryHighResKVAttention(nn.Module):"""方案 1: 低分辨率特征 (Query) 查询高分辨率特征 (Key, Value).输出分辨率与低分辨率输入相同。"""def __…...

A2A JS SDK 完整教程:快速入门指南
目录 什么是 A2A JS SDK?A2A JS 安装与设置A2A JS 核心概念创建你的第一个 A2A JS 代理A2A JS 服务端开发A2A JS 客户端使用A2A JS 高级特性A2A JS 最佳实践A2A JS 故障排除 什么是 A2A JS SDK? A2A JS SDK 是一个专为 JavaScript/TypeScript 开发者设计的强大库ÿ…...

给网站添加live2d看板娘
给网站添加live2d看板娘 参考文献: stevenjoezhang/live2d-widget: 把萌萌哒的看板娘抱回家 (ノ≧∇≦)ノ | Live2D widget for web platformEikanya/Live2d-model: Live2d model collectionzenghongtu/live2d-model-assets 前言 网站环境如下,文章也主…...

十九、【用户管理与权限 - 篇一】后端基础:用户列表与角色模型的初步构建
【用户管理与权限 - 篇一】后端基础:用户列表与角色模型的初步构建 前言准备工作第一部分:回顾 Django 内置的 `User` 模型第二部分:设计并创建 `Role` 和 `UserProfile` 模型第三部分:创建 Serializers第四部分:创建 ViewSets第五部分:注册 API 路由第六部分:后端初步测…...
