C++二分查找算法:132模式枚举3简洁版
本文涉及的基础知识点
二分查找算法合集
本题不同解法
| 包括题目及代码 | C++二分查找算法:132 模式解法一枚举3 |
| C++二分查找算法:132 模式解法二枚举2 | |
| 代码简洁 | C++二分查找算法:132 模式解法三枚举1 |
| 性能最佳 | C++单调向量算法:132 模式解法三枚举1 |
| 代码更简洁 | C++二分查找算法:132模式枚举3简洁版 |
分析
时间复杂度
总时间复杂度O(nlogn),枚举3时间复杂度O(n),查询2是否复杂度O(logn)。
思路
如果有多个候选1,选取最小的那个,所以我们不需要记录所有的1,只需要记录最小值iLeftMin。2必须大于iLeftMin,且小于3。
也就是setRight中第一个大于iLeftMin的数,是否小于nums[j]。
核心代码
class Solution{
public:bool find132pattern(vector<int>&nums) {m_c = nums.size();if (m_c < 3){m_iIndex3 = -1;return false;}int iLeftMin = nums.front();std::multiset<int> setRight(nums.begin()+2,nums.end());for (int j = 1; j + 1 < m_c; j++){auto it = setRight.upper_bound(iLeftMin);if ((setRight.end() != it)&&(*it < nums[j])){m_iIndex3 = j;return true;}iLeftMin = min(iLeftMin, nums[j]);setRight.erase(setRight.find(nums[j+1]));}return false;}vector<int> m_v2To1;//v[i]等于j表示nums[i] >=nsum[j],如果有多个合法的j,取最小值,如果不存在,v[i]=m_c。int m_iIndex3 = -1;int m_c;
};
测试用例
template
void Assert(const T& t1, const T& t2)
{
assert(t1 == t2);
}
template
void Assert(const vector& v1, const vector& v2)
{
if (v1.size() != v2.size())
{
assert(false);
return;
}
for (int i = 0; i < v1.size(); i++)
{
Assert(v1[i], v2[i]);
}
}
int main()
{
vector nums;
bool res;
{
Solution slu;
nums = { 3,5,0,3,4 };
res = slu.find132pattern(nums);
//Assert(vector{5, 0, 5, 2, 0}, slu.m_v2To1);
Assert(1, slu.m_iIndex3);
Assert(true, res);
}
{
nums = { 1 ,2, 3,4 };
res = Solution().find132pattern(nums);
Assert(false, res);
}
{
Solution slu;
nums = { 3,1,4,2 };
res = slu.find132pattern(nums);
//Assert(vector{4, 4, 0, 1}, slu.m_v2To1);
Assert(2, slu.m_iIndex3);
Assert(true, res);
}
{
Solution slu;
nums = { -1,3,2,0 };
res = slu.find132pattern(nums);
//Assert(vector{4, 0, 0, 0}, slu.m_v2To1);
Assert(1, slu.m_iIndex3);
Assert(true, res);
}
{
Solution slu;
nums = { 1, 4, 0, -1, -2, -3, -1, -2 };
res = slu.find132pattern(nums);
//Assert(vector{4, 0, 0, 0}, slu.m_v3To1);
//Assert(5, slu.m_iIndex3);
Assert(true, res);
}
{
Solution slu;
nums = { 2};
res = slu.find132pattern(nums);
//Assert(vector{5, 0, 5, 2, 0}, slu.m_v2To1);
Assert(-1, slu.m_iIndex3);
Assert(true, res);
}
//CConsole::Out(res);
}
扩展阅读
视频课程
有效学习:明确的目标 及时的反馈 拉伸区(难度合适),可以先学简单的课程,请移步CSDN学院,听白银讲师(也就是鄙人)的讲解。
https://edu.csdn.net/course/detail/38771
如何你想快
速形成战斗了,为老板分忧,请学习C#入职培训、C++入职培训等课程
https://edu.csdn.net/lecturer/6176
相关下载
想高屋建瓴的学习算法,请下载《喜缺全书算法册》doc版
https://download.csdn.net/download/he_zhidan/88348653
| 我想对大家说的话 |
|---|
| 闻缺陷则喜是一个美好的愿望,早发现问题,早修改问题,给老板节约钱。 |
| 墨子曰:事无终始,无务多业。也就是我们常说的专业的人做专业的事。 |
| 如果程序是一条龙,那算法就是他的是睛 |
相关文章:

C++二分查找算法:132模式枚举3简洁版
本文涉及的基础知识点 二分查找算法合集 本题不同解法 包括题目及代码C二分查找算法:132 模式解法一枚举3C二分查找算法:132 模式解法二枚举2代码简洁C二分查找算法:132 模式解法三枚举1性能最佳C单调向量算法:132 模式解法三枚…...

Map 和 WeakMap:JavaScript 中的键值对集合
JavaScript 是一种动态、弱类型的脚本语言,经常用于构建现代 Web 应用程序。在编写 JavaScript 代码时,我们经常需要使用各种数据结构来存储和管理数据。其中,Map 和 WeakMap 就是两个非常有用的数据结构,它们分别提供了用于存储键…...
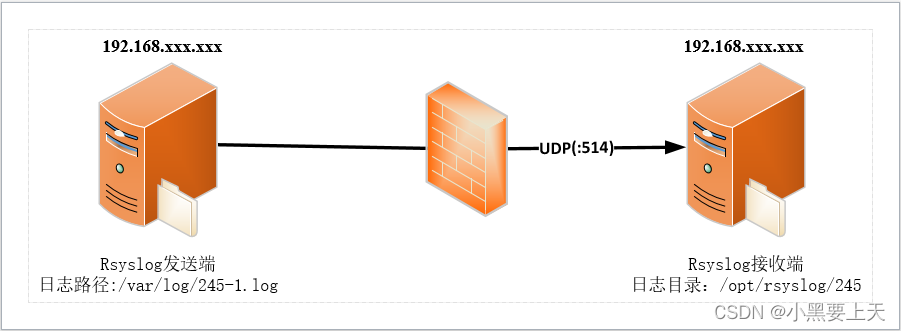
linux rsyslog综合实战1
本次我们通过rsyslog服务将A节点服务器上的单个日志(Path:/var/log/245-1.log)实时同步到B节点服务器目录下(Path:/opt/rsyslog/245) 1.rsyslog架构 2.环境信息 环境信息 HostnameIpAddressOS versionModuleNotersyslog1192.168.10.245CentOS Linux release 7.9.2009 (Core)rs…...
redis+python 建立免费http-ip代理池;验证+留接口
前言: 效果图: 对于网络上的一些免费代理ip,http的有效性还是不错的;但是,https的可谓是凤毛菱角; 正巧,有一个web可以用http访问,于是我就想到不如直接拿着免费的HTTP代理去做这个! 思路: 1.单页获取ipporttime (获取time主要是为了后面使用的时候,依照时效可以做文章) 2.整…...
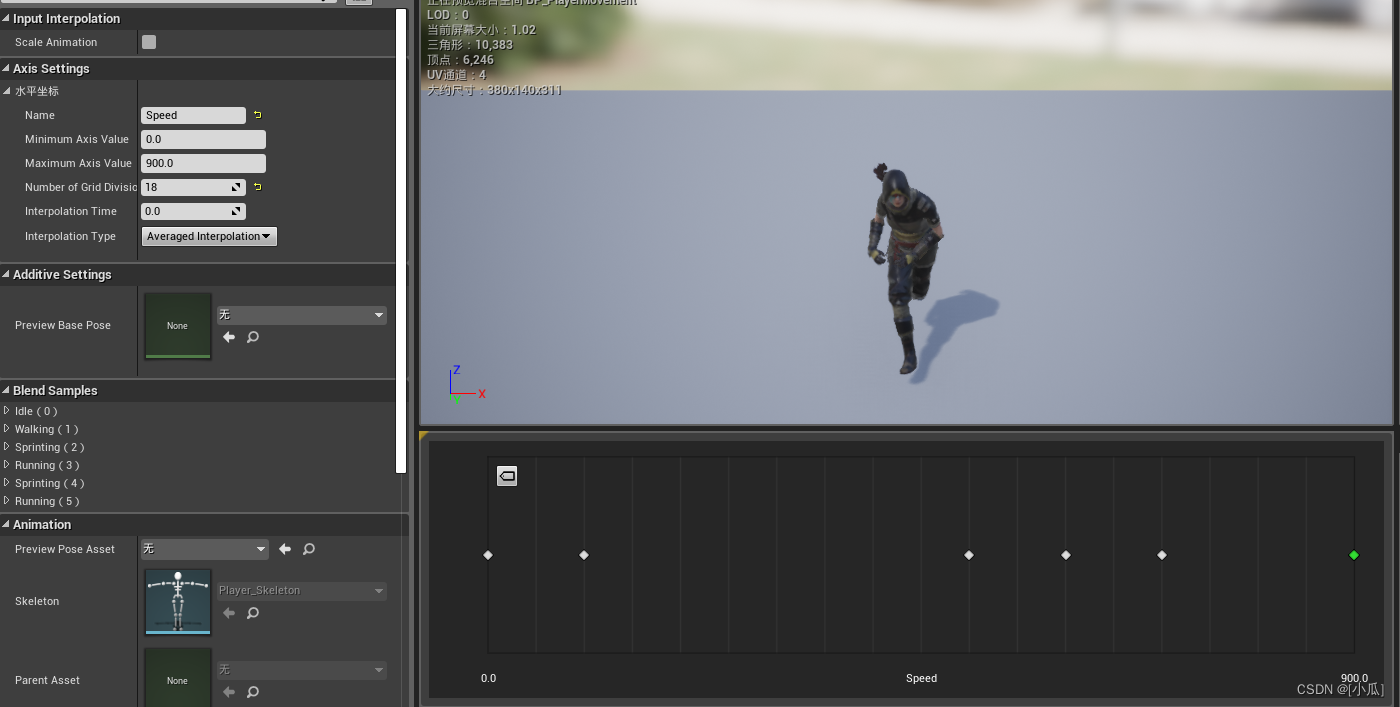
虚幻C++ day5
角色状态的常见机制 创建角色状态设置到UI上 在MainPlayer.h中新建血量,最大血量,耐力,最大耐力,金币变量,作为角色的状态 //主角状态UPROPERTY(EditDefaultsOnly, BlueprintReadOnly, Category "Playe Stats&…...

C#中的DateTime类
C# 中的 DateTime 类是用于表示日期和时间的结构。它提供了一系列属性和方法,用于处理日期和时间的各种操作和计算。下面是一些常用的 DateTime 类的用法和方法解释,以及相应的示例说明: 创建 DateTime 对象: 使用当前日期和时间创…...

Flutter笔记:Matrix4矩阵变换与案例
Flutter笔记 Matrix4矩阵变换及其案例 作者:李俊才 (jcLee95):https://blog.csdn.net/qq_28550263 邮箱 :291148484163.com 本文地址:https://blog.csdn.net/qq_28550263/article/details/134474764 【简介…...

数字IC前端学习笔记:时钟切换电路
相关阅读 数字IC前端https://blog.csdn.net/weixin_45791458/category_12173698.html?spm1001.2014.3001.5482 有些时候我们需要在系统运行时切换系统时钟,最简单的方法就是使用一个MUX(数据选择器)选择输出的时钟,如下代码片所…...
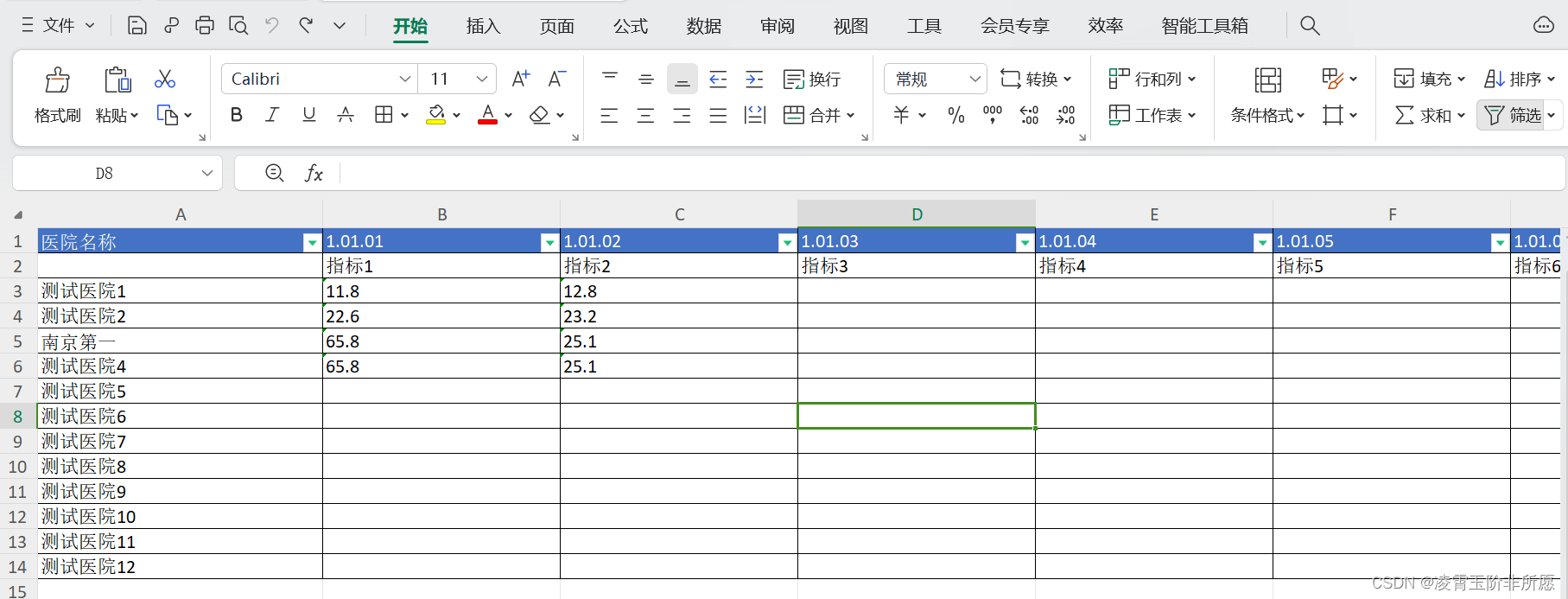
.NET6使用MiniExcel根据数据源横向导出头部标题及数据
.NET6MiniExcel根据数据源横向导出头部标题 MiniExcel简单、高效避免OOM的.NET处理Excel查、写、填充数据工具。 特点: 低内存耗用,避免OOM、频繁 Full GC 情况 支持即时操作每行数据 兼具搭配 LINQ 延迟查询特性,能办到低消耗、快速分页等复杂查询 轻量…...

表内容的操作(增删查改)【MySQL】
文章目录 表的 CRUDCreate(增加)插入记录插入冲突则更新记录替换记录 Retrieve(查找)查找记录指定表达式的别名为结果去重WHERE 子句运算符条件查询区间查询模糊查询空值查询 对结果排序筛选分页结果 Update(修改&…...

C++快速入门 - 2(几分钟让你快速入门C++)
C快速入门 - 2 1. 内联函数1.1 概念1.2 特性 2. auto关键字(C11)2.1 类型别名思考2.2 auto简介2.3 auto的使用细则2.4 auto不能推导的场景 3. 基于范围的for循环(C11)3.1 范围for的语法3.2 范围for的使用条件 1. 内联函数 1.1 概念 以inline修饰的函数叫做内联函数,…...

Excel自定义函数提取超链接
通过自定义函数的方法,批量提取超链接 首选开启开发工具选项 文件-选项-自定义功能区-勾选开发工具选项-确认 AltF11或者直接点击跳转到开发工具-Visual Basic 在左上方VBA project空白处右键点击空白区域-插入-模块 在弹出的窗口中输入以下命令定义GetURL函数 F…...

计算矩阵边缘元素之和
Description 输入一个整数矩阵,计算位于矩阵边缘的元素之和。所谓矩阵边缘的元素,就是第一行和最后一行的元素以及第一列和最后一列的元素。 Input 第一行分别为矩阵的行数m和列数n(m<100,n<100),…...

回归预测 | Matlab实现HPO-ELM猎食者算法优化极限学习机的数据回归预测
回归预测 | Matlab实现HPO-ELM猎食者算法优化极限学习机的数据回归预测 目录 回归预测 | Matlab实现HPO-ELM猎食者算法优化极限学习机的数据回归预测效果一览基本介绍程序设计参考资料 效果一览 基本介绍 Matlab实现HPO-ELM猎食者算法优化极限学习机的数据回归预测(…...
)
Flutter笔记:目录与文件存储以及在Flutter中的使用(下)
Flutter笔记 目录与文件存储以及在Flutter中的使用(下) 文件读写与Flutter中文件管理 作者:李俊才 (jcLee95):https://blog.csdn.net/qq_28550263 邮箱 :291148484163.com 本文地址:…...
机器学习笔记 - Ocr识别中的CTC算法原理概述
一、文字识别 在文本检测步骤中,分割出了文本区域。现在需要识别这些片段中存在哪些文本。 机器学习笔记 - Ocr识别中的文本检测EAST网络概述-CSDN博客文章浏览阅读300次。在 EAST 网络的这个分支中,它合并了 VGG16 网络不同层的特征输出。现在,该层之后的特征大小将等于 p…...
系列二、Lock接口
一、多线程编程模板 线程 操作 资源类 高内聚 低耦合 二、实现步骤 1、创建资源类 2、资源类里创建同步方法、同步代码块 三、12306卖票程序 3.1、synchronized实现 3.1.1、Ticket /*** Author : 一叶浮萍归大海* Date: 2023/11/20 8:54* …...
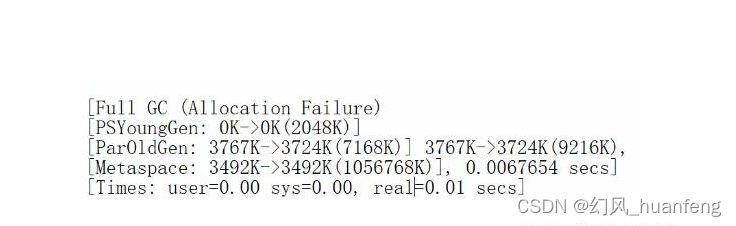
JVM虚拟机:通过日志学习PS+PO垃圾回收器
我们刚才设置参数的时候看到了-XXPrintGCDetails表示输出详细的GC处理日志,那么我们如何理解这个日志呢?日志是有规则的,我们需要按照这个规则来理解日志中的内容,它有两个格式,一个格式是GC的格式(新生代&…...

从0开始学习JavaScript--JavaScript使用Promise
JavaScript中的异步编程一直是开发中的重要话题。传统的回调函数带来了回调地狱和代码可读性的问题。为了解决这些问题,ES6引入了Promise,一种更现代、更灵活的异步编程解决方案。本文将深入探讨JavaScript中如何使用Promise,通过丰富的示例代…...
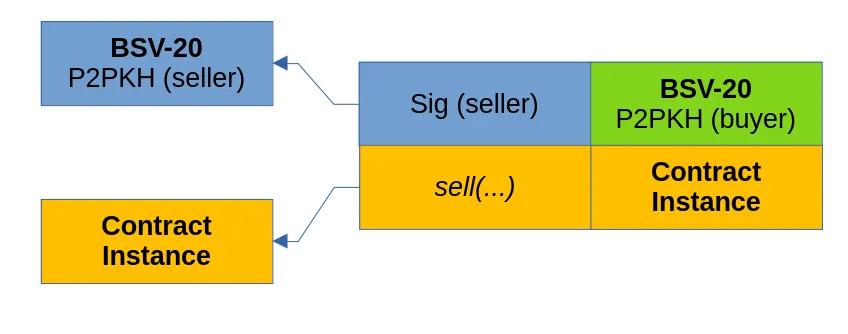
使用契约的链上限价订单
我们开发了链上限价订单。 它基于一种称为契约的智能合约,只有在花费输出的交易满足特定条件时才可以花费输出。 为了演示其工作原理,我们实施了以比特币支付的 Ordinals 代币买卖限价订单,无需托管人。 它可以运行在任何比特币协议链上&…...

从零实现富文本编辑器#5-编辑器选区模型的状态结构表达
先前我们总结了浏览器选区模型的交互策略,并且实现了基本的选区操作,还调研了自绘选区的实现。那么相对的,我们还需要设计编辑器的选区表达,也可以称为模型选区。编辑器中应用变更时的操作范围,就是以模型选区为基准来…...

通过Wrangler CLI在worker中创建数据库和表
官方使用文档:Getting started Cloudflare D1 docs 创建数据库 在命令行中执行完成之后,会在本地和远程创建数据库: npx wranglerlatest d1 create prod-d1-tutorial 在cf中就可以看到数据库: 现在,您的Cloudfla…...

uni-app学习笔记二十二---使用vite.config.js全局导入常用依赖
在前面的练习中,每个页面需要使用ref,onShow等生命周期钩子函数时都需要像下面这样导入 import {onMounted, ref} from "vue" 如果不想每个页面都导入,需要使用node.js命令npm安装unplugin-auto-import npm install unplugin-au…...

【项目实战】通过多模态+LangGraph实现PPT生成助手
PPT自动生成系统 基于LangGraph的PPT自动生成系统,可以将Markdown文档自动转换为PPT演示文稿。 功能特点 Markdown解析:自动解析Markdown文档结构PPT模板分析:分析PPT模板的布局和风格智能布局决策:匹配内容与合适的PPT布局自动…...

DIY|Mac 搭建 ESP-IDF 开发环境及编译小智 AI
前一阵子在百度 AI 开发者大会上,看到基于小智 AI DIY 玩具的演示,感觉有点意思,想着自己也来试试。 如果只是想烧录现成的固件,乐鑫官方除了提供了 Windows 版本的 Flash 下载工具 之外,还提供了基于网页版的 ESP LA…...

C++ 基础特性深度解析
目录 引言 一、命名空间(namespace) C 中的命名空间 与 C 语言的对比 二、缺省参数 C 中的缺省参数 与 C 语言的对比 三、引用(reference) C 中的引用 与 C 语言的对比 四、inline(内联函数…...

python如何将word的doc另存为docx
将 DOCX 文件另存为 DOCX 格式(Python 实现) 在 Python 中,你可以使用 python-docx 库来操作 Word 文档。不过需要注意的是,.doc 是旧的 Word 格式,而 .docx 是新的基于 XML 的格式。python-docx 只能处理 .docx 格式…...

浅谈不同二分算法的查找情况
二分算法原理比较简单,但是实际的算法模板却有很多,这一切都源于二分查找问题中的复杂情况和二分算法的边界处理,以下是博主对一些二分算法查找的情况分析。 需要说明的是,以下二分算法都是基于有序序列为升序有序的情况…...

均衡后的SNRSINR
本文主要摘自参考文献中的前两篇,相关文献中经常会出现MIMO检测后的SINR不过一直没有找到相关数学推到过程,其中文献[1]中给出了相关原理在此仅做记录。 1. 系统模型 复信道模型 n t n_t nt 根发送天线, n r n_r nr 根接收天线的 MIMO 系…...

以光量子为例,详解量子获取方式
光量子技术获取量子比特可在室温下进行。该方式有望通过与名为硅光子学(silicon photonics)的光波导(optical waveguide)芯片制造技术和光纤等光通信技术相结合来实现量子计算机。量子力学中,光既是波又是粒子。光子本…...
