传递函数的推导和理解
传递函数的推导和理解
假设有一个线性系统,在一般情况下,它的激励 x ( t ) x(t) x(t)与响应 y ( t ) y(t) y(t)所满足的的关系,可用下列微分方程来表示:
a n y ( n ) + a n − 1 y ( n − 1 ) + a n − 2 y ( n − 2 ) + ⋯ + a 1 y ′ + a 0 y = b m x ( m ) + b m − 1 x ( m − 1 ) + b m − 2 x ( m − 2 ) + ⋯ + b 1 x ′ + b 0 x (1) \begin{array}{l}{a_n}{y^{(n)}} + {a_{n - 1}}{y^{(n - 1)}} + {a_{n - 2}}{y^{(n - 2)}} + \cdots + {a_1}y' + {a_0}y\\ = {b_m}{x^{({\rm{m}})}} + {b_{m - 1}}{x^{({\rm{m - 1}})}} + {b_{m - 2}}{x^{({\rm{m - 2}})}} + \cdots + {b_1}x' + {b_0}x\end{array}\tag1 any(n)+an−1y(n−1)+an−2y(n−2)+⋯+a1y′+a0y=bmx(m)+bm−1x(m−1)+bm−2x(m−2)+⋯+b1x′+b0x(1)
其中, a 0 , a 1 , ⋯ , a n , b 0 , b 1 , ⋯ , b m {a_0},{a_1}, \cdots ,{a_n},{b_0},{b_1}, \cdots ,{b_m} a0,a1,⋯,an,b0,b1,⋯,bm均为常数, m , n m,n m,n为正整数, n ≥ m n \ge m n≥m
设 L [ y ( t ) ] = Y ( s ) , L [ x ( t ) ] = X ( s ) \mathscr{L}[y(t)]=Y(s),\mathscr{L}[x(t)]=X(s) L[y(t)]=Y(s),L[x(t)]=X(s),根据Laplace变换的微分性质,有
L [ a k y ( k ) ] = a k s k Y ( s ) − a k [ s k − 1 y ( 0 ) + s k − 2 y ′ ( 0 ) + s k − 3 y ′ ′ ( 0 ) + ⋯ + s k − ( k − 1 ) y ( k − 2 ) ( 0 ) + s 0 y ( k − 1 ) ( 0 ) ] ( k = 0 , 1 , 2 , ⋯ , n ) {\mathscr L}[{a_k}{y^{(k)}}] = {a_k}{s^k}Y(s) - {a_k}[{s^{k - 1}}y(0) + {s^{k - 2}}y'(0) + {s^{k - 3}}y''(0) + \cdots + {s^{k - (k - 1)}}{y^{(k - 2)}}(0) + {s^0}{y^{(k - 1)}}(0)]\\(k = 0,1,2, \cdots ,n) L[aky(k)]=akskY(s)−ak[sk−1y(0)+sk−2y′(0)+sk−3y′′(0)+⋯+sk−(k−1)y(k−2)(0)+s0y(k−1)(0)](k=0,1,2,⋯,n)
L [ b k x ( k ) ] = b k s k X ( s ) − b k [ s k − 1 x ( 0 ) + s k − 2 x ′ ( 0 ) + s k − 3 x ′ ′ ( 0 ) + ⋯ + s k − ( k − 1 ) x ( k − 2 ) ( 0 ) + s 0 x ( k − 1 ) ( 0 ) ] ( k = 0 , 1 , 2 , ⋯ , m ) {\mathscr L}[{b_k}{x^{(k)}}] = {b_k}{s^k}X(s) - {b_k}[{s^{k - 1}}x(0) + {s^{k - 2}}x'(0) + {s^{k - 3}}x''(0) + \cdots + {s^{k - (k - 1)}}{x^{(k - 2)}}(0) + {s^0}{x^{(k - 1)}}(0)] \\(k = 0,1,2, \cdots ,m) L[bkx(k)]=bkskX(s)−bk[sk−1x(0)+sk−2x′(0)+sk−3x′′(0)+⋯+sk−(k−1)x(k−2)(0)+s0x(k−1)(0)](k=0,1,2,⋯,m)
对式子(1)两边进行Laplace变换并通过整理,可得:
D ( s ) Y ( s ) − M h y ( s ) = M ( s ) X ( s ) − M h x ( s ) D(s)Y(s) - {M_{hy}}(s) = M(s)X(s) - {M_{hx}}(s) D(s)Y(s)−Mhy(s)=M(s)X(s)−Mhx(s)
即:
Y ( s ) = M ( s ) D ( s ) X ( s ) + M h y ( s ) − M h x ( s ) D ( s ) (2) Y(s) = \frac{{M(s)}}{{D(s)}}X(s) + \frac{{{M_{hy}}(s) - {M_{hx}}(s)}}{{D(s)}}\tag2 Y(s)=D(s)M(s)X(s)+D(s)Mhy(s)−Mhx(s)(2)
其中,
D ( s ) = a n s n + a n − 1 s n − 1 + ⋯ + a 1 s + a 0 , D(s) = {a_n}{s^n} + {a_{n - 1}}{s^{n - 1}} + \cdots + {a_1}s + {a_0}, D(s)=ansn+an−1sn−1+⋯+a1s+a0,
M ( s ) = b m s m + b m − 1 s m − 1 + ⋯ + b 1 s + b 0 , M(s) = {b_m}{s^m} + {b_{m - 1}}{s^{m - 1}} + \cdots + {b_1}s + {b_0}, M(s)=bmsm+bm−1sm−1+⋯+b1s+b0,
M h y ( s ) = a n y ( 0 ) s n − 1 + [ a n y ′ ( 0 ) + a n − 1 y ( 0 ) ] s n − 2 + [ a n y ′ ′ ( 0 ) + a n − 1 y ′ ( 0 ) + a n − 2 y ( 0 ) ] s n − 3 + ⋯ + [ a n y ( n − 2 ) ( 0 ) + a n − 1 y ( n − 3 ) ( 0 ) + ⋯ + a 2 y ( 0 ) ] s + [ a n y ( n − 1 ) ( 0 ) + a n − 1 y ( n − 2 ) ( 0 ) + ⋯ + a 1 y ( 0 ) ] , {M_{hy}}(s) = {a_n}y(0){s^{n - 1}} + [{a_n}y'(0) + {a_{n - 1}}y(0)]{s^{n - 2}} + [{a_n}y''(0) + {a_{n - 1}}y'(0) + {a_{n - 2}}y(0)]{s^{n - 3}} + \cdots + [{a_n}{y^{(n - 2)}}(0) + {a_{n - 1}}{y^{(n - 3)}}(0) + \cdots + {a_2}y(0)]s + [{a_n}{y^{(n - 1)}}(0) + {a_{n - 1}}{y^{(n - 2)}}(0) + \cdots + {a_1}y(0)], Mhy(s)=any(0)sn−1+[any′(0)+an−1y(0)]sn−2+[any′′(0)+an−1y′(0)+an−2y(0)]sn−3+⋯+[any(n−2)(0)+an−1y(n−3)(0)+⋯+a2y(0)]s+[any(n−1)(0)+an−1y(n−2)(0)+⋯+a1y(0)],
M h x ( s ) = b m x ( 0 ) s m − 1 + [ b m x ′ ( 0 ) + b m − 1 x ( 0 ) ] s m − 2 + [ b m x ′ ′ ( 0 ) + b m − 1 x ′ ( 0 ) + b m − 2 x ( 0 ) ] s m − 3 + ⋯ + [ b m x ( m − 2 ) ( 0 ) + b m − 1 x ( m − 3 ) ( 0 ) + ⋯ + b 2 x ( 0 ) ] s + [ b m x ( m − 1 ) ( 0 ) + b m − 1 x ( n − 2 ) ( 0 ) + ⋯ + b 1 x ( 0 ) ] , {M_{hx}}(s) = {b_m}x(0){s^{m - 1}} + [{b_m}x'(0) + {b_{m - 1}}x(0)]{s^{m - 2}} + [{b_m}x''(0) + {b_{m - 1}}x'(0) + {b_{m - 2}}x(0)]{s^{m - 3}} + \cdots + [{b_m}{x^{(m - 2)}}(0) + {b_{m - 1}}{x^{(m - 3)}}(0) + \cdots + {b_2}x(0)]s + [{b_m}{x^{(m - 1)}}(0) + {b_{m - 1}}{x^{(n - 2)}}(0) + \cdots + {b_1}x(0)], Mhx(s)=bmx(0)sm−1+[bmx′(0)+bm−1x(0)]sm−2+[bmx′′(0)+bm−1x′(0)+bm−2x(0)]sm−3+⋯+[bmx(m−2)(0)+bm−1x(m−3)(0)+⋯+b2x(0)]s+[bmx(m−1)(0)+bm−1x(n−2)(0)+⋯+b1x(0)],
若令 G ( s ) = M ( s ) G ( s ) G(s) = \frac{{M(s)}}{{G(s)}} G(s)=G(s)M(s), G h ( s ) = M h y ( s ) − M h x ( s ) D ( s ) {G_h}(s) = \frac{{{M_{hy}}(s) - {M_{hx}}(s)}}{{D(s)}} Gh(s)=D(s)Mhy(s)−Mhx(s),则式(2)可写为:
Y ( s ) = G ( s ) X ( s ) + G h ( s ) (3) Y(s) = G(s)X(s) + {G_h}(s)\tag3 Y(s)=G(s)X(s)+Gh(s)(3)
式子中:
G ( s ) = b m s m + b m − 1 s m − 1 + ⋯ + b 1 s + b 0 a n s n + a n − 1 s n − 1 + ⋯ + a 1 s + a 0 (4) G(s) = \frac{{{b_m}{s^m} + {b_{m - 1}}{s^{m - 1}} + \cdots + {b_1}s + {b_0}}}{{{a_n}{s^n} + {a_{n - 1}}{s^{n - 1}} + \cdots + {a_1}s + {a_0}}}\tag4 G(s)=ansn+an−1sn−1+⋯+a1s+a0bmsm+bm−1sm−1+⋯+b1s+b0(4)
我们称 G ( s ) G(s) G(s)为系统的传递函数。它表达了系统本身的特性,而与激励及系统的初始状态无关。
但是 G h ( s ) G_{h}(s) Gh(s)则由激励和系统本身的初值条件所决定。若这些初始条件全为0,即 G h ( s ) G_{h}(s) Gh(s)=0时,式子(3)可写成:
Y ( s ) = G ( s ) X ( s ) 或 G ( s ) = Y ( s ) X ( s ) (5) \begin{array}{l}Y(s) = G(s)X(s) 或 G(s) = \frac{{Y(s)}}{{X(s)}}\end{array}\tag5 Y(s)=G(s)X(s)或G(s)=X(s)Y(s)(5)
式子(5)表明,在零初值条件下,系统的传递函数等于其响应的Laplace变换与其激励的Laplace变换之比。
因此,当我们知道系统的传递函数后,就可以由系统的激励按照式子(3)或式子(5)求出其响应的拉普拉斯变换 Y ( s ) Y(s) Y(s),再通过求逆变换可得其响应 y ( t ) y(t) y(t)。
系统的激励 x ( t ) x(t) x(t),系统的响应 y ( t ) y(t) y(t),以及它们的拉普拉斯变换 X ( s ) X(s) X(s), Y ( s ) Y(s) Y(s)和传递函数的关系如图1所示。
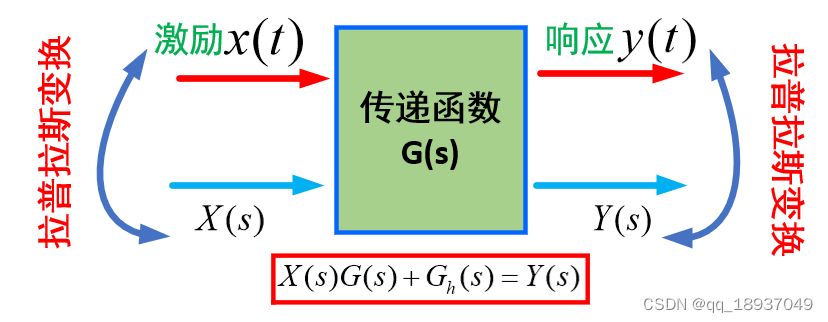
图1 系统激励、响应以及传递函数之间的关系
需要说明的是,传递函数不表明系统的物理性质。许多性质不同的物理系统,可以有相同的传递函数。而传递函数不同的物理系统,即使系统的激励相同,其响应也是不相同的,因此,对传递函数的分析和研究,就能统一处理各种物理性质不同的额线性系统。
简而言之,通过对系统微分方程进行拉普拉斯变换,推导出了系统的传递函数 G ( s ) G(s) G(s)。
相关文章:

传递函数的推导和理解
传递函数的推导和理解 假设有一个线性系统,在一般情况下,它的激励 x ( t ) x(t) x(t)与响应 y ( t ) y(t) y(t)所满足的的关系,可用下列微分方程来表示: a n y ( n ) a n − 1 y ( n − 1 ) a n − 2 y ( n − 2 ) ⋯ a 1 y…...

STM32 SPI
SPI介绍 SPI是Serial Pepheral interface缩写,串行外围设备接口。 SPI接口是一种高速的全双工同步通信总线,已经广泛应用在众多MCU、存储芯片、AD转换器和LCD之间。大部分STM32有3个SPI接口,本实验使用的是SPI1。 SPI同一时刻既能发送数据&…...
Linux系统编程 day02 vim、gcc、库的制作与使用
Linux系统编程 day02 vim、gcc、库的制作与使用 01. vim0101. 命令模式下的操作0102. 切换到文本输入模式0103. 末行模式下的操作0104. vim的配置文件 02. gcc03. 库的制作与使用0301. 静态库的制作与使用0302. 动态库(共享库)的制作与使用 01. vim vim是一个编辑器࿰…...

Mistral 7B 比Llama 2更好的开源大模型 (四)
Mistral 7B在平衡高性能和保持大型语言模型高效的目标方面迈出了重要的一步。通过我们的工作,我们的目标是帮助社区创建更实惠、更高效、更高性能的语言模型,这些模型可以在广泛的现实世界应用程序中使用。 Mistral 7B在实践中,对于16K和W=4096的序列长度,对FlashAttentio…...

相似基因序列问题 ——查找
【题目背景】 生物的遗传物质存在个体间或种群水平的差异,这样的差异被称为遗传变异。突变及基因重组等因素都会导致遗传变异。尽管亲代在将其遗传信息传递给子代时会发生遗传变异,但是这些遗传变异仅占遗传物质的一小部分,通常亲代和子代之…...
【汇编】“转移”综述、操作符offset、jmp指令
文章目录 前言一、转移综述1.1 :背景:1.2 转移指令1.3 转移指令的分类按转移行为根据指令对IP修改的范围不同 二、操作符offset2.1 offset操作符是干什么的?标号是什么? 2.2 nop是什么? 三、jmp指令3.1 jmp指令的功能3.2 jmp指令&…...
Java格式化类Format
文章目录 Format介绍Format方法- format(格式化)- parseObject(解析) 格式化分类日期时间格式化1. DateFormat常用方法getInstancegetDateInstancegetTimeInstancegetDateTimeInstance 方法入参styleLocale 2. SimpleDateFormat常…...

力扣每日一题-美化数组的最少删除数-2023.11.21
力扣每日一题:美化数组的最少删除数 开篇 今天的力扣每日一题居然写出来了,好开心,迫不及待地把题目分享出来,希望你也能把它狠狠拿下。 题目链接: 2216.美化数组的最少删除数 题目描述 代码思路 创建一个list集合来保存数组&a…...
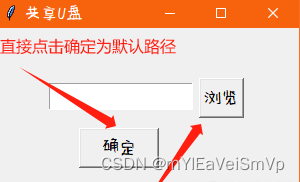
【练习】检测U盘并自动复制内容到电脑的软件
软件作用: 有U盘插在电脑上后,程序会检测到U盘的路径。 自己可以提前设置一个保存复制文件的路径或者使用为默认保存的复制路径(默认为桌面,可自行修改)。 检测到U盘后程序就会把U盘的文件复制到电脑对应的…...
【计算机毕业设计】Springboot高校论文管理系统 -96280,免费送源码,【开题选题+程序定制+论文书写+答辩ppt书写-原创定制程序】
SpringBoot论文管理系统 摘 要 随着科学技术的飞速发展,社会的方方面面、各行各业都在努力与现代的先进技术接轨,通过科技手段来提高自身的优势,高校当然也不例外。论文管理系统是以实际运用为开发背景,运用软件工程原理和开发方…...

nginx 代理接口报404 问题排查
今天遇到一个nginx代理后端接口请求报404的问题,问题是这样的,后端由于服务器没有环境,但是需要和前端联调,于是采用cpolar内网穿透的方式,穿出来了。但是前端请求跨域,于是前端用nginx代理了一下后端接口&…...

JVM 调优指南
文章目录 为什么要学 JVM一、JVM 整体布局二、Class 文件规范三、类加载模块四、执行引擎五、GC 垃圾回收1 、JVM内存布局2 、 JVM 有哪些主要的垃圾回收器?3 、分代垃圾回收工作机制 六、对 JVM 进行调优的基础思路七、 GC 情况分析实例 JVM调优指南 -- 楼兰 JV…...

澳洲猫罐头如何?我亲自喂养过的优质猫罐头分享
猫罐头要符合三点:营养配方完整均衡、原料新鲜优质、生产工艺科学可靠。只有具备这些特点,才是品质上乘的猫罐头。 猫罐头的三个要素,一个都不能少。配方不均衡,营养就不足;原料不新鲜,生产出来的猫罐头就…...

CISP练习测试题
免责声明 文章仅做经验分享用途,切勿当真,未授权的攻击属于非法行为!利用本文章所提供的信息而造成的任何直接或者间接的后果及损失,均由使用者本人负责,作者不为此承担任何责任,一旦造成后果请自行承担!!! 某公司准备在业务环境中部署一种新的计算机产品,下列哪一项…...
2023下半年软件设计师考试知识点大全思维导图
软件设计师考试知识点大全思维导图 2023年下半年第一次机考 复习资料 以上是我在学习过程中根据自己的知识结构的特点及刷到的考题 做的导图,有需要的可以留言发原版的 mmap格式文件 方便自己拓展. 软考资料 这是网上找的资料 汇总免费放在这里 吧
[C++ 从入门到精通] 12.重载运算符、赋值运算符重载、析构函数
📢博客主页:https://loewen.blog.csdn.net📢欢迎点赞 👍 收藏 ⭐留言 📝 如有错误敬请指正!📢本文由 丶布布原创,首发于 CSDN,转载注明出处🙉📢现…...

Android Binder 跨进程通信的优势是什么
Android Binder 跨进程通信的优势是什么 Android Binder 是 Android 系统中用于实现跨进程通信的底层机制,具有以下优势: 高效性:Android Binder 使用共享内存技术,在进程间传递数据时不需要进行数据拷贝,从而提高了传…...

HashMap的详细解读
HashMap是Java语言中的一个重要数据结构,它实现了Map接口,允许我们存储键值对,并且可以根据键直接访问对应的值。 特性 键值对存储:HashMap存储的是键值对数据,可以方便的通过键来获取值。无序:HashMap中…...
10个好用的Mac数据恢复软件推荐—恢复率高达99%
如果您正在寻找最好的 Mac 数据恢复软件来检索意外删除或丢失的文件,那么这里就是您的最佳选择。 我们理解,当您找不到 Mac 计算机或外部驱动器上保存的一些重要文件时,会感到多么沮丧和绝望。这些文件非常珍贵,无论出于何种原因…...
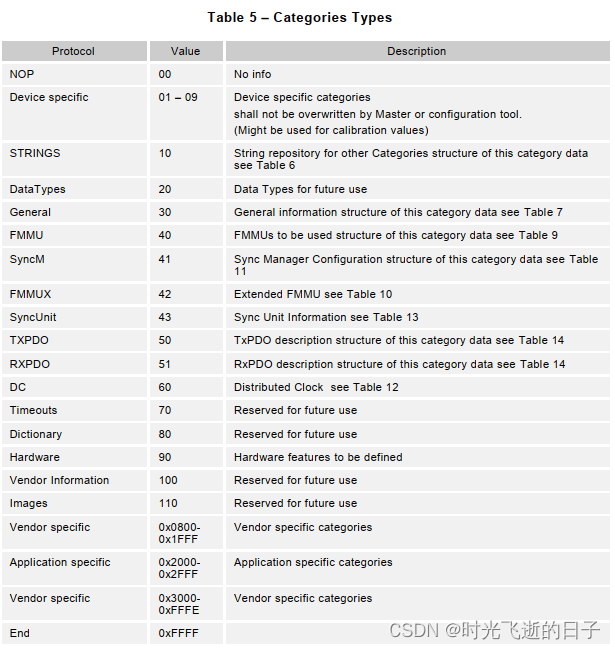
EtherCAT从站EEPROM分类附加信息详解:RXPDO(输入过程数据对象)
0 工具准备 1.EtherCAT从站EEPROM数据(本文使用DE3E-556步进电机驱动器)1 分类附加信息——RXPDO(输入过程数据对象) 1.1 分类附加信息规范 在EEPROM字64开始的区域存储的是分类附加信息,这里存储了包括设备信息、SM配置、FMMU配置在内的诸多信息。每个信息在一段连续的…...

龙虎榜——20250610
上证指数放量收阴线,个股多数下跌,盘中受消息影响大幅波动。 深证指数放量收阴线形成顶分型,指数短线有调整的需求,大概需要一两天。 2025年6月10日龙虎榜行业方向分析 1. 金融科技 代表标的:御银股份、雄帝科技 驱动…...

在鸿蒙HarmonyOS 5中实现抖音风格的点赞功能
下面我将详细介绍如何使用HarmonyOS SDK在HarmonyOS 5中实现类似抖音的点赞功能,包括动画效果、数据同步和交互优化。 1. 基础点赞功能实现 1.1 创建数据模型 // VideoModel.ets export class VideoModel {id: string "";title: string ""…...

Qwen3-Embedding-0.6B深度解析:多语言语义检索的轻量级利器
第一章 引言:语义表示的新时代挑战与Qwen3的破局之路 1.1 文本嵌入的核心价值与技术演进 在人工智能领域,文本嵌入技术如同连接自然语言与机器理解的“神经突触”——它将人类语言转化为计算机可计算的语义向量,支撑着搜索引擎、推荐系统、…...

什么是EULA和DPA
文章目录 EULA(End User License Agreement)DPA(Data Protection Agreement)一、定义与背景二、核心内容三、法律效力与责任四、实际应用与意义 EULA(End User License Agreement) 定义: EULA即…...

【决胜公务员考试】求职OMG——见面课测验1
2025最新版!!!6.8截至答题,大家注意呀! 博主码字不易点个关注吧,祝期末顺利~~ 1.单选题(2分) 下列说法错误的是:( B ) A.选调生属于公务员系统 B.公务员属于事业编 C.选调生有基层锻炼的要求 D…...

工业自动化时代的精准装配革新:迁移科技3D视觉系统如何重塑机器人定位装配
AI3D视觉的工业赋能者 迁移科技成立于2017年,作为行业领先的3D工业相机及视觉系统供应商,累计完成数亿元融资。其核心技术覆盖硬件设计、算法优化及软件集成,通过稳定、易用、高回报的AI3D视觉系统,为汽车、新能源、金属制造等行…...

学校时钟系统,标准考场时钟系统,AI亮相2025高考,赛思时钟系统为教育公平筑起“精准防线”
2025年#高考 将在近日拉开帷幕,#AI 监考一度冲上热搜。当AI深度融入高考,#时间同步 不再是辅助功能,而是决定AI监考系统成败的“生命线”。 AI亮相2025高考,40种异常行为0.5秒精准识别 2025年高考即将拉开帷幕,江西、…...
)
Angular微前端架构:Module Federation + ngx-build-plus (Webpack)
以下是一个完整的 Angular 微前端示例,其中使用的是 Module Federation 和 npx-build-plus 实现了主应用(Shell)与子应用(Remote)的集成。 🛠️ 项目结构 angular-mf/ ├── shell-app/ # 主应用&…...

【深尚想】TPS54618CQRTERQ1汽车级同步降压转换器电源芯片全面解析
1. 元器件定义与技术特点 TPS54618CQRTERQ1 是德州仪器(TI)推出的一款 汽车级同步降压转换器(DC-DC开关稳压器),属于高性能电源管理芯片。核心特性包括: 输入电压范围:2.95V–6V,输…...

Win系统权限提升篇UAC绕过DLL劫持未引号路径可控服务全检项目
应用场景: 1、常规某个机器被钓鱼后门攻击后,我们需要做更高权限操作或权限维持等。 2、内网域中某个机器被钓鱼后门攻击后,我们需要对后续内网域做安全测试。 #Win10&11-BypassUAC自动提权-MSF&UACME 为了远程执行目标的exe或者b…...
