机器人走迷宫问题
题目
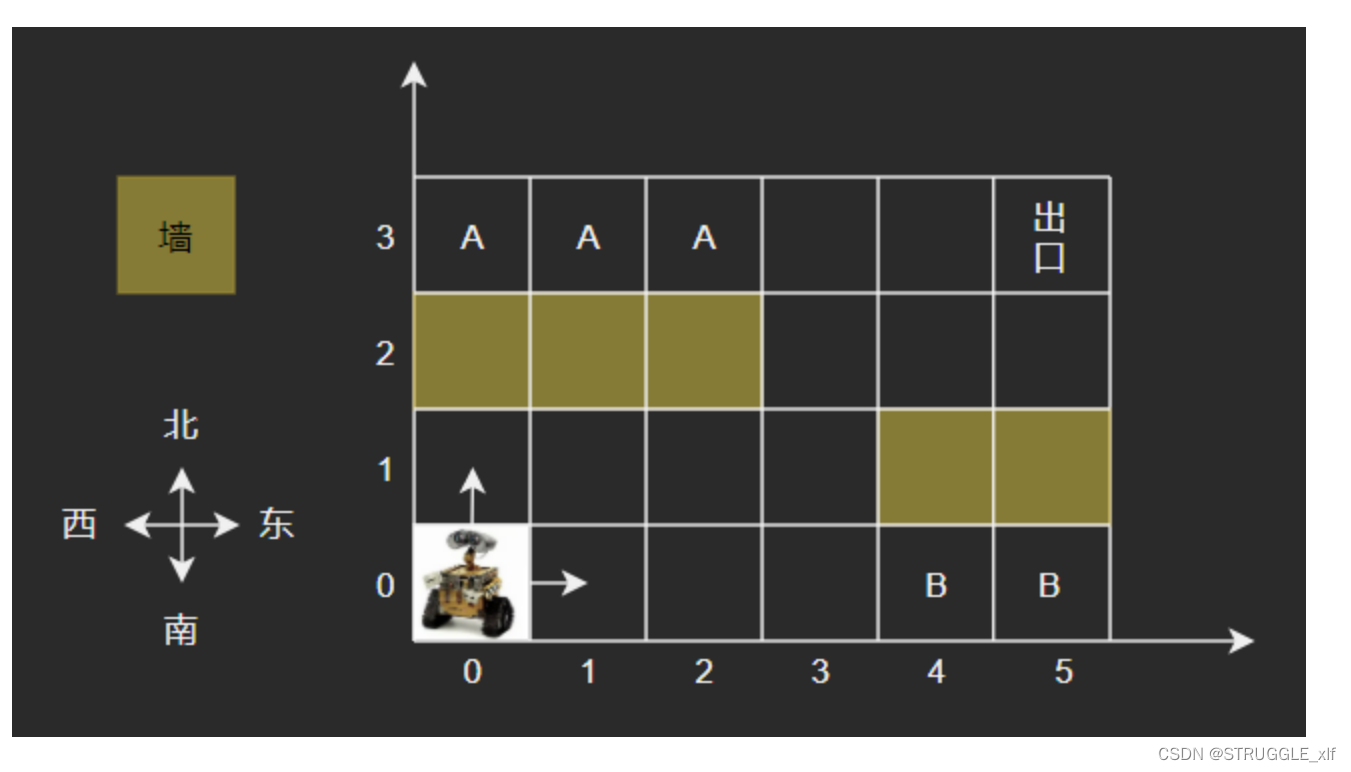
1.房间有XY的方格组成,例如下图为64的大小。每一个方格以坐标(x,y) 描述。
2.机器人固定从方格(0, 0)出发,只能向东或者向北前进,出口固定为房间的最东北角,如下图的
方格(5,3)。用例保证机器人可以从入口走到出口。
3.房间有些方格是墙壁,如(4,1) ,机器人不能经过那儿。
4.有些地方是- -旦到达就无法走到出口的,如标记为B的方格,称之为陷阱方格。
5.有些地方是机器人无法达到的,如标记为A的方格,称之为不可达方格,不可达方格不包括墙壁
所在的位置
6.如下实例图中,陷阱方格有2个,不可达方格有3个。
7.请为该机器人实现路径规划功能:给定房间大小,墙壁位置,请计算出陷阱方格与不可达方格分别有多少个
输入
1.第一-行为房间的x和y(0 < x,y <= 1000 )
2.第二行为房间中墙壁的个数N (O <= N < x*Y)
3.接着下面会有N行墙壁的坐标
同一行中如果有多个数据以一个空格隔开,用例保证所有的输入数据均合法,(结尾不带回车换行
输出
1.陷阱方格与不可达方格数量,两个信息在一行中输出, 以一个空格隔开。(结尾不带回车换行)

Java代码
package day11;import javax.print.attribute.standard.Chromaticity;
import java.util.HashSet;
import java.util.Objects;
import java.util.Scanner;
import java.util.Set;public class MazeSolving {static int xLength;static int yLength;static class CheckModel{int x;int y;public CheckModel(int x,int y){this.x = x;this.y = y;}@Overridepublic int hashCode(){return Objects.hash(x, y);}@Overridepublic boolean equals(Object o){if(o==this){return true;}if(o==null||getClass()!=o.getClass()){return false;}CheckModel check = (CheckModel) o;return x == check.x && y==check.y;}}//wallSet代表墙壁坐标,checkSet用于存储在搜索路径过程中检查过的坐标,finishSet用于存储已经找到终点的坐标private static void findItOut(int x, int y, Set<CheckModel> wallSet, Set<CheckModel> checkSet, Set<CheckModel> finishSet) {if(yLength-1==y&&xLength-1==x){finishSet.add(new CheckModel(x,y));//检查当前坐标 (x, y) 是否是迷宫的终点}if(yLength<=y||x>=xLength){return; //越界了}checkSet.add(new CheckModel(x,y));//否则添加到已检查坐标//北方向if(!wallSet.contains(new CheckModel(x,y+1))){findItOut(x,y+1,wallSet,checkSet,finishSet);}else{finishSet.add(new CheckModel(x,y));}//东方向if(!wallSet.contains(new CheckModel(x+1,y))){findItOut(x+1,y,wallSet,checkSet,finishSet);}else{finishSet.add(new CheckModel(x,y));}}public static void main(String[] args){try {Scanner sc = new Scanner(System.in);xLength = sc.nextInt();yLength = sc.nextInt();int size = sc.nextInt();int[][] values = new int[size][2];for(int i = 0; i < size; i++){values[i][0] = sc.nextInt();values[i][1] = sc.nextInt();}int trapCount = 0;int invalidCount = 0;Set<CheckModel> wallHashSet = new HashSet<>();for(int[] wall:values){wallHashSet.add(new CheckModel(wall[0],wall[1]));}Set<CheckModel> checksHashSet = new HashSet<>();Set<CheckModel> finshHashSet = new HashSet<>();findItOut(0,0,wallHashSet,checksHashSet,finshHashSet);invalidCount = xLength*yLength-checksHashSet.size()-wallHashSet.size();//整个迷宫中的格子数减去检查过的格子数和包含障碍物的格子数等于无法到达数量/** 这里使用 finishHashSet 中的每个坐标作为起点,再次调用 findItOut 进行深度优先搜索。* 如果搜索得到的路径中不包含终点 (xLength - 1, yLength - 1),则说明这条路径是无效的,* trapCount 就会增加。这样,trapCount 表示的是无效的路径的数量。** */for(CheckModel model:finshHashSet){Set<CheckModel> checksT = new HashSet<>();Set<CheckModel> finishT = new HashSet<>();findItOut(model.x, model.y, wallHashSet,checksT,finishT);if(!finishT.contains(new CheckModel(xLength-1,yLength-1))){trapCount++;}}System.out.println(trapCount+" "+invalidCount);}catch (Exception e){e.printStackTrace();System.out.println("input error");}}}相关文章:

机器人走迷宫问题
题目 1.房间有XY的方格组成,例如下图为64的大小。每一个方格以坐标(x,y) 描述。 2.机器人固定从方格(0, 0)出发,只能向东或者向北前进,出口固定为房间的最东北角,如下图的 方格(5,3)。用例保证机器人可以从入口走到出口。 3.房间…...

轻量封装WebGPU渲染系统示例<36>- 广告板(Billboard)(WGSL源码)
原理不再赘述,请见wgsl shader实现。 当前示例源码github地址: https://github.com/vilyLei/voxwebgpu/blob/feature/rendering/src/voxgpu/sample/BillboardEntityTest.ts 当前示例运行效果: WGSL顶点shader: group(0) binding(0) var<uniform> objMat :…...

Java 多线程进阶
1 方法执行与进程执行 GetMapping("/demo1")public void demo1(){//方法调用new ThreadTest1("run1").run();//线程调用new ThreadTest1("run2").start();} 下断点调试信息,可以看到run()方法当前线程是“main1” 继续运行到run里面&…...

CentOS上搭建SVN并自动同步至web目录
一、搭建svn环境并创建仓库: 1、安装Subversion: yum install svn2、创建版本库: //先建目录 cd /www mkdir wwwsvn cd wwwsvn //创建版本库 svnadmin create xiangmumingcheng二、创建用户组及用户: 1、 进入版本库中的配…...
.Net中Redis的基本使用
前言 Redis可以用来存储、缓存和消息传递。它具有高性能、持久化、高可用性、扩展性和灵活性等特点,尤其适用于处理高并发业务和大量数据量的系统,它支持多种数据结构,如字符串、哈希表、列表、集合、有序集合等。 Redis的使用 安装包Ser…...
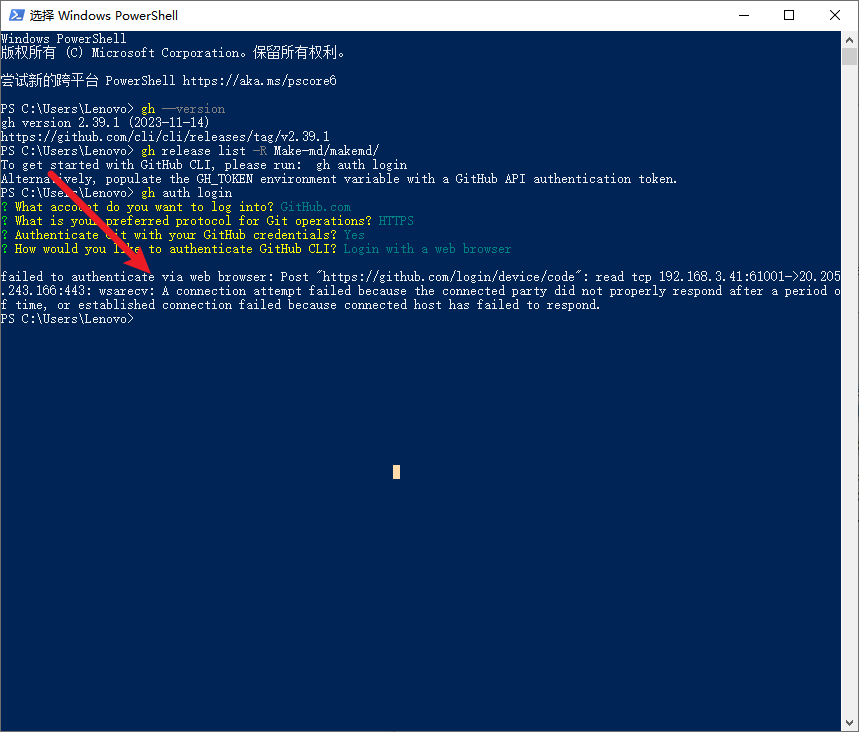
使用cli批量下载GitHub仓库中所有的release
文章目录 1\. 引言2\. 工具官网3\. 官方教程4\. 测试用的网址5\. 安装5.1. 使用winget安装5.2. 查看gh是否安装成功了 6\. 使用6.1. 进行GitHub授权6.1.1. 授权6.1.2. 授权成功6.2 查看指定仓库中的所有版本的release6.2.1. 默认的30个版本6.2.2. 自定义的100个版本6.3 下载特定…...
深入分析TaskView源码之触摸相关
问题背景 hi,粉丝朋友们: 大家好!android 10以后TaskView作为替代ActivityView的容器,在课程的分屏pip自由窗口专题也进行了相关的详细介绍分析。 这里再补充一下相关的TaskView和桌面内嵌情况下的触摸分析 主要问题点ÿ…...
键盘快捷键工具Keyboard Maestro mac中文版介绍
Keyboard Maestro mac是一款键盘快捷键工具,它可以帮助用户通过自定义快捷键来快速完成各种操作,提高工作效率。Keyboard Maestro支持多种快捷键组合,包括单键、双键、三键、四键组合等,用户可以根据自己的习惯进行设置。此外&…...
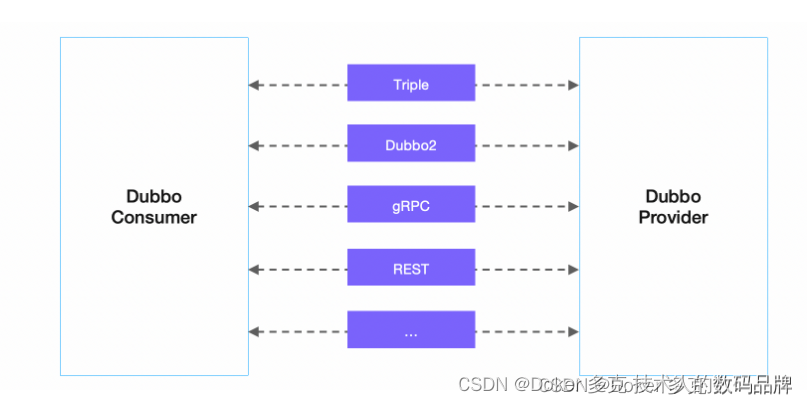
Dubbo开发系列
一、概述 以上是 Dubbo 的工作原理图,从抽象架构上分为两层:服务治理抽象控制面 和 Dubbo 数据面 。 服务治理控制面。服务治理控制面不是特指如注册中心类的单个具体组件,而是对 Dubbo 治理体系的抽象表达。控制面包含协调服务发现的注册中…...
)
周赛372(正难则反、枚举+贪心、异或位运算、离线+单调栈)
文章目录 周赛372[2937. 使三个字符串相等](https://leetcode.cn/problems/make-three-strings-equal/)模拟(正难则反) [2938. 区分黑球与白球](https://leetcode.cn/problems/separate-black-and-white-balls/)枚举 贪心 [2939. 最大异或乘积](https:/…...
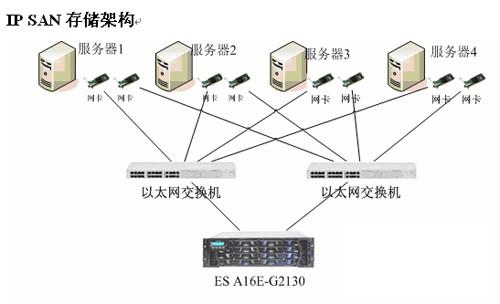
存储区域网络(SAN)之FC-SAN和IP-SAN的比较
存储区域网络(Storage Area Network,SAN)用于将多个系统连接到存储设备和子系统。 早期FC-SAN: 采用光纤通道(Fibre Channel,FC)技术,通过光纤通道交换机连接存储阵列和服务器主机,建立专用于数据存储的区域网络。 传…...

Leetcode_45:跳跃游戏 II
题目描述: 给定一个长度为 n 的 0 索引整数数组 nums。初始位置为 nums[0]。 每个元素 nums[i] 表示从索引 i 向前跳转的最大长度。换句话说,如果你在 nums[i] 处,你可以跳转到任意 nums[i j] 处: 0 < j < nums[i] i j < n 返…...

给新手教师的成长建议
随着教育的不断发展和进步,越来越多的新人加入到教师这个行列中来。从学生到教师,这是一个华丽的转身,需要我们不断地学习和成长。作为一名新手老师,如何才能快速成长呢?以下是一名老师教师给的几点建议: 一…...

新手教师如何迅速成长
对于许多新手教师来说,迈出教学的第一步可能会感到非常困难。不过,通过一些关键的策略和技巧,还是可以快速提升教学能力的,我将为大家提供一些实用的建议,帮助各位在教育领域迅速成长。 深入了解学科知识 作为一名老师…...
竞赛选题 深度学习验证码识别 - 机器视觉 python opencv
文章目录 0 前言1 项目简介2 验证码识别步骤2.1 灰度处理&二值化2.2 去除边框2.3 图像降噪2.4 字符切割2.5 识别 3 基于tensorflow的验证码识别3.1 数据集3.2 基于tf的神经网络训练代码 4 最后 0 前言 🔥 优质竞赛项目系列,今天要分享的是 &#x…...
提升工作效率,使用AnyTXT Searcher实现远程办公速查公司电脑文件——“cpolar内网穿透”
文章目录 前言1. AnyTXT Searcher1.1 下载安装AnyTXT Searcher 2. 下载安装注册cpolar3. AnyTXT Searcher设置和操作3.1 AnyTXT结合cpolar—公网访问搜索神器3.2 公网访问测试 4. 固定连接公网地址 前言 你是否遇到过这种情况,异地办公或者不在公司,想找…...

mybatis使用foreach标签实现union集合操作
最近遇到一个场景就是Java开发中,需要循环多个表名,然后用同样的查询操作分别查表,最终得到N个表中查询的结果集合。在查询内容不一致时Java中跨表查询常用的是遍历表名集合循环查库,比较耗费资源,效率较低。在查询内容…...

请问DasViewer是否支持与业务系统集成,将业务的动态的数据实时的展示到三维模型上?
答:一般这种是以平台的方式来展示,云端地球实景三维建模云平台是专门做这一块的,可前往云端地球官网免费使用。 DasViewer是由大势智慧自主研发的免费的实景三维模型浏览器,采用多细节层次模型逐步自适应加载技术,让用户在极低的电脑配置下,…...

[ruby on rails]rack-cors, rack-attack
gem rack-attack gem rack-cors1. rack-attack 可以根据ip、域名等设置黑名单、设置访问频率 设置黑名单 # 新增 config/initializers/rack_attack.rb # 请求referer如果匹配不上设置的allowed_origins,返回403 forbidden Rack::Attack.blocklist(block bad domai…...
猫12分类:使用多线程爬取图片的Python程序
本文目标 对于猫12目标检测部分的数据集,采用网络爬虫来制作数据集。 在网络爬虫中,经常需要下载大量的图片。为了提高下载效率,可以使用多线程来并发地下载图片。本文将介绍如何使用Python编写一个多线程爬虫程序,用于爬取图片…...
)
Java 语言特性(面试系列2)
一、SQL 基础 1. 复杂查询 (1)连接查询(JOIN) 内连接(INNER JOIN):返回两表匹配的记录。 SELECT e.name, d.dept_name FROM employees e INNER JOIN departments d ON e.dept_id d.dept_id; 左…...

对WWDC 2025 Keynote 内容的预测
借助我们以往对苹果公司发展路径的深入研究经验,以及大语言模型的分析能力,我们系统梳理了多年来苹果 WWDC 主题演讲的规律。在 WWDC 2025 即将揭幕之际,我们让 ChatGPT 对今年的 Keynote 内容进行了一个初步预测,聊作存档。等到明…...

ios苹果系统,js 滑动屏幕、锚定无效
现象:window.addEventListener监听touch无效,划不动屏幕,但是代码逻辑都有执行到。 scrollIntoView也无效。 原因:这是因为 iOS 的触摸事件处理机制和 touch-action: none 的设置有关。ios有太多得交互动作,从而会影响…...

什么是Ansible Jinja2
理解 Ansible Jinja2 模板 Ansible 是一款功能强大的开源自动化工具,可让您无缝地管理和配置系统。Ansible 的一大亮点是它使用 Jinja2 模板,允许您根据变量数据动态生成文件、配置设置和脚本。本文将向您介绍 Ansible 中的 Jinja2 模板,并通…...

学校时钟系统,标准考场时钟系统,AI亮相2025高考,赛思时钟系统为教育公平筑起“精准防线”
2025年#高考 将在近日拉开帷幕,#AI 监考一度冲上热搜。当AI深度融入高考,#时间同步 不再是辅助功能,而是决定AI监考系统成败的“生命线”。 AI亮相2025高考,40种异常行为0.5秒精准识别 2025年高考即将拉开帷幕,江西、…...

【数据分析】R版IntelliGenes用于生物标志物发现的可解释机器学习
禁止商业或二改转载,仅供自学使用,侵权必究,如需截取部分内容请后台联系作者! 文章目录 介绍流程步骤1. 输入数据2. 特征选择3. 模型训练4. I-Genes 评分计算5. 输出结果 IntelliGenesR 安装包1. 特征选择2. 模型训练和评估3. I-Genes 评分计…...

rnn判断string中第一次出现a的下标
# coding:utf8 import torch import torch.nn as nn import numpy as np import random import json""" 基于pytorch的网络编写 实现一个RNN网络完成多分类任务 判断字符 a 第一次出现在字符串中的位置 """class TorchModel(nn.Module):def __in…...

Linux 内存管理实战精讲:核心原理与面试常考点全解析
Linux 内存管理实战精讲:核心原理与面试常考点全解析 Linux 内核内存管理是系统设计中最复杂但也最核心的模块之一。它不仅支撑着虚拟内存机制、物理内存分配、进程隔离与资源复用,还直接决定系统运行的性能与稳定性。无论你是嵌入式开发者、内核调试工…...

深度学习水论文:mamba+图像增强
🧀当前视觉领域对高效长序列建模需求激增,对Mamba图像增强这方向的研究自然也逐渐火热。原因在于其高效长程建模,以及动态计算优势,在图像质量提升和细节恢复方面有难以替代的作用。 🧀因此短时间内,就有不…...

【JVM】Java虚拟机(二)——垃圾回收
目录 一、如何判断对象可以回收 (一)引用计数法 (二)可达性分析算法 二、垃圾回收算法 (一)标记清除 (二)标记整理 (三)复制 (四ÿ…...
