洛谷 U91193:棋盘覆盖问题 ← 分治法
【题目来源】
https://www.luogu.com.cn/problem/U91193
【问题描述】
在一个2^k * 2^k(k≥0)个方格组成的棋盘中,恰有一个方格与其他方格不同,称该方格为一特殊方格。现在用4种不同形状的 L型(占3小格)骨牌覆盖棋盘上除了特殊方格以外的所有方格,且各骨牌不能重叠。 步骤为:将棋盘一分为四,依次处理左上角,右上角,左下角,右下角,递归进行。严格按照这个顺序处理。
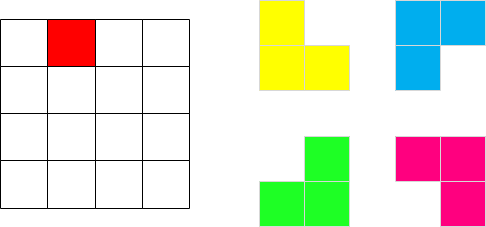
例如,一种用不同形状的 L型骨牌覆盖填充的策略如下图所示:

【输入格式 】
输入三个数k,x,y,分别表示棋盘大小,特殊方格位置。
【输出格式】
共2^k行,每行2^k个数,每辆个数中间空格隔开。
输出按照上述顺序所覆盖的棋盘。特殊方格用0表示,其他为骨牌编号。
【算法分析】
应用分治法求解棋盘覆盖问题的技巧在于如何划分棋盘,要求是使划分后的子棋盘的大小相同,从而将原来规模较大的棋盘覆盖问题分解为规模较小的棋盘覆盖问题。
其常用技巧是,当 时,将
的棋盘划分为4个
的子棋盘。由于原棋盘只有一个特殊方格,所以这样划分后,这4个子棋盘中只有一个子棋盘包含该特殊方格,其余3个子棋盘中没有特殊方格。然后,用一个L型骨盘覆盖这3个没有特殊方格的子棋盘的会合处,并将这三个子棋盘上被L型骨牌覆盖的方格标记为新的特殊方格。递归地使用这种分割方法,直至棋盘简化为
的棋盘,就结束递归。(注意:下图中的红色特殊方格,可以在其所在子棋盘的任意位置。下图只是示意需要选择的位置。)
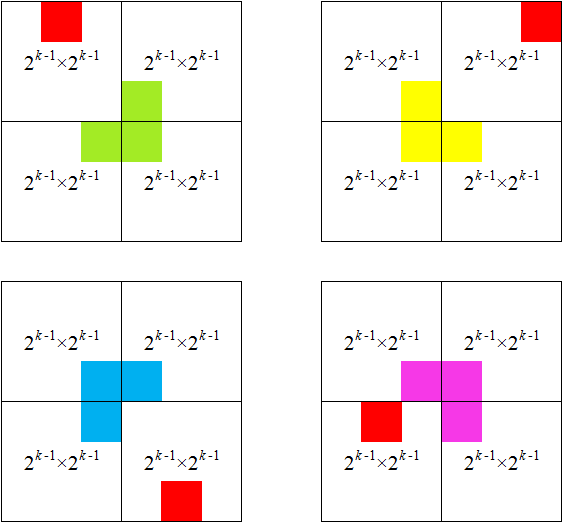
上图用语言表述为:
◆左上的子棋盘(若不存在特殊方格)----则将该子棋盘右下角的那个方格假设为特殊方格
◆右上的子棋盘(若不存在特殊方格)----则将该子棋盘左下角的那个方格假设为特殊方格
◆左下的子棋盘(若不存在特殊方格)----则将该子棋盘右上角的那个方格假设为特殊方格
◆右下的子棋盘(若不存在特殊方格)----则将该子棋盘左上角的那个方格假设为特殊方格
【数据范围】
说明/提示:k<=5
【算法代码】
#include <bits/stdc++.h>
using namespace std;
const int maxn=1005;
int ans[maxn][maxn];
int id;void solve(int x1,int y1,int x2,int y2,int sz) {if(sz==1) return;int t=++id;sz/=2;int midx=x1+sz-1;int midy=y1+sz-1;if(x2<=midx && y2<=midy) { //特殊方格在左上部分,继续划分solve(x1,y1,x2,y2,sz);} else {ans[midx][midy]=t; //不在左上,覆盖左上部分的右下角solve(x1,y1,midx,midy,sz); //继续划分}if(x2<=midx && y2>midy) { //特殊方格在右上部分,继续划分solve(x1,y1+sz,x2,y2,sz);} else {ans[midx][midy+1]=t; //不在右上,覆盖右上部分的左下角solve(x1,y1+sz,midx,midy+1,sz); //继续划分}if(x2>midx && y2<=midy) { //特殊方格在左下部分,继续划分solve(x1+sz,y1,x2,y2,sz);} else {ans[midx+1][midy]=t; //不在左下,覆盖左下部分的右上角solve(x1+sz,y1,midx+1,midy,sz); //继续划分}if(x2>midx && y2>midy) { //特殊方格在右下部分,继续划分solve(x1+sz,y1+sz,x2,y2,sz);} else {ans[midx+1][midy+1]=t; //不在右下,覆盖右下部分的左上角solve(x1+sz,y1+sz,midx+1,midy+1,sz); //继续划分}
}int main() {int k,x,y;cin>>k>>x>>y;int size=(1<<k);solve(1,1,x,y,size);for(int i=1; i<=size; i++)for(int j=1; j<=size; j++) {if(j==size) printf("%d\n",ans[i][j]);else printf("%d ",ans[i][j]);}return 0;
}/*
3
1 1
ans:0 3 4 4 8 8 9 93 3 2 4 8 7 7 95 2 2 6 10 10 7 115 5 6 6 1 10 11 11
13 13 14 1 1 18 19 19
13 12 14 14 18 18 17 19
15 12 12 16 20 17 17 21
15 15 16 16 20 20 21 21
*/
【参考文献】
https://blog.csdn.net/ljw_study_in_CSDN/article/details/106409784
https://www.codenong.com/cs105800665/
https://www.cnblogs.com/crx234/p/5988055.html
https://www.cnblogs.com/yanyu01/p/8734212.html
https://blog.csdn.net/scliu12345/article/details/102387130
相关文章:

洛谷 U91193:棋盘覆盖问题 ← 分治法
【题目来源】https://www.luogu.com.cn/problem/U91193【问题描述】 在一个2^k * 2^k(k≥0)个方格组成的棋盘中,恰有一个方格与其他方格不同,称该方格为一特殊方格。现在用4种不同形状的 L型(占3小格)骨牌覆…...

基于OMAPL138+FPGA核心板多核软件开发组件MCSDK开发入门(下)
本文测试板卡为创龙科技 SOM-TL138F 是一款基于 TI OMAP-L138(定点/浮点 DSP C674x + ARM9)+ 紫光同创 Logos/Xilinx Spartan-6 低功耗 FPGA 处理器设计的工业级核心板。核心板内部OMAP-L138 与 Logos/Spartan-6 通过 uPP、EMIFA、I2C 通信总线连接,并通过工业级 B2B连接器引…...

熵,线性规划,半监督自监督聚类打标签
1.熵 信息熵是消除不确定性所需信息量的度量。 信息熵就是信息的不确定程度,信息熵越小,信息越确定。 对象的信息熵是正比于它的概率的负对数的,也就是 I©−log(pc) 其中n为事件的所有可能性。 为什么使用交叉熵?在机器学习…...
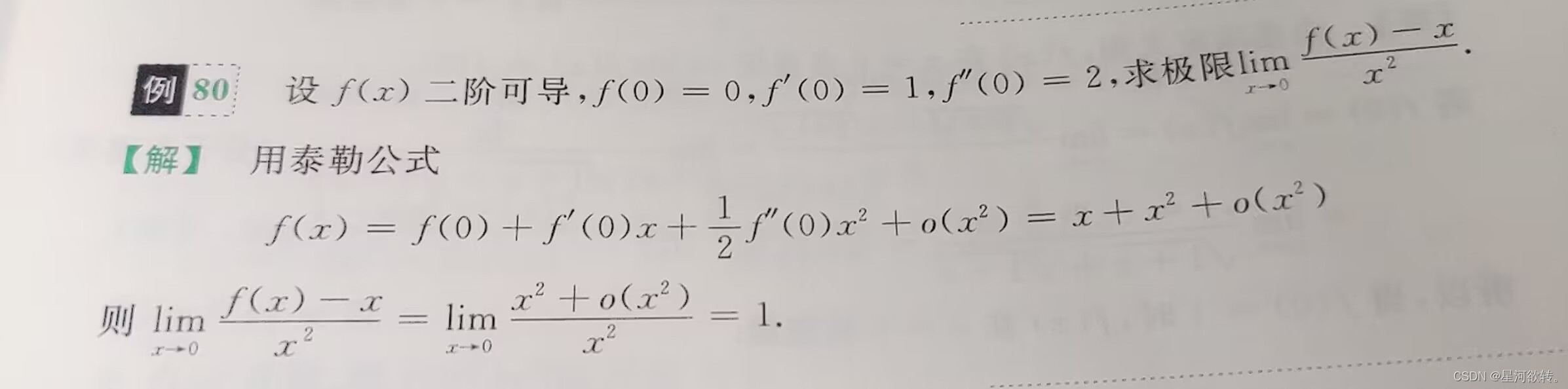
求极限方法总结
1.利用四则运算法则求极限 2.利用两个重要极限求极限 //0除以0型 //1的无穷次方型 3.利用等价无穷小替换替换求极限 //在等价替换时注意和差项 4.利用洛必达法则求极限 5.利用夹逼准则求极限 6.利用单调有界数列极限准则求极限 7.利用无穷小的性质求极限 8.利用函数的连续性…...

Flutter Scrollable 中ViewPort滚动原理
关于Flutter Sliver组件内容可以参考下面这位博主博客,写的已经非常好了,这里就不再赘述。 38、Flutter之 可滚动组件简介_flutter 可滑动_风雨「83」的博客-CSDN博客 通过阅读上面的博客,我们已经知道了Scrollable和Viewport基础概念&#…...

多目标粒子群结合极限学习机ELM求解帕累托前沿,MOPSO-ELM
目录 背影 parte前沿的定义 注意事项 基于多目标粒子群结合极限学习机的帕累托前沿求解帕累托前沿 主要参数 MATLAB代码 效果图 结果分析 展望 背影 在目标优化过程种,很多时候都两个或者多个目标,并且目标函数不能同时达到最优,鱼与熊掌不可兼得,这个时候可以通过求解帕…...
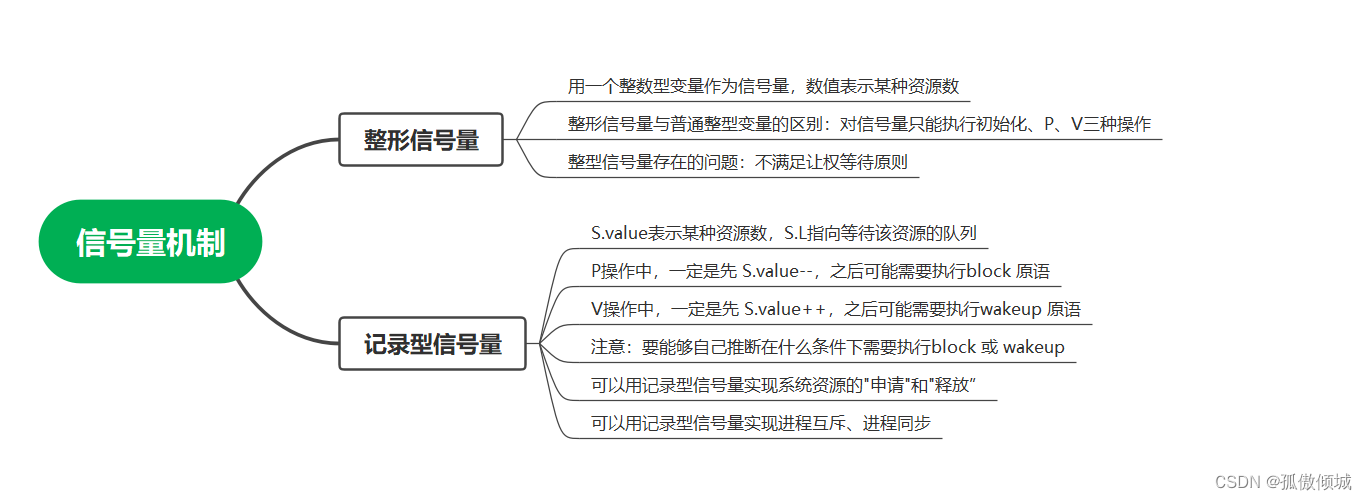
(二十)操作系统-信号量机制
文章目录一、知识预览二、前篇文章知识点回顾三、信号量机制四、信号量机制—整形信号量五、信号量机制—记录型信号量六、总结一、知识预览 二、前篇文章知识点回顾 进程互斥的四种软件实现方式:单标志法、双标志先检查、双标志后检查、Peterson算法。(…...

ceph osd slow ops 检测
目的 常用的方法检测 ceph slow 问题 参考 yceph -scluster:id: 22908555-e596-4c2d-a1f6-34fcf4d3e935health: HEALTH_WARNDegraded data redundancy: 46384/12805029 objects degraded (0.362%), 145 pgs degraded, 122 pgs undersized309 slow ops, oldest one blocked…...

百度CTO王海峰:深度学习平台+大模型,夯实产业智能化基座
2月27日,中国人工智能学会首届智能融合产业论坛在成都顺利举办。本届论坛由中国人工智能学会(CAAI)主办,中国人工智能学会智能融合专委会、百度公司、深度学习技术及应用国家工程研究中心和电子科技大学联合承办。中国工程院多名院…...

【C++】vector的基本使用
难道向上攀爬的那条路,不是比站在顶峰更让人热血沸腾吗? 文章目录一、vector和string的联系与不同二、vector的扩容操作1.resize() (缺省值为匿名对象)&& reserve()2.reserve在g和vs上的扩容机制3.reserve异地扩容和shri…...

社交媒体营销的5个好处
有些人认为,社交媒体营销不能直接与销售挂钩。这就是为什么在制定营销策略时,社交媒体营销会被部分人忽视的原因。然而,与其他广告渠道不同,社交媒体是双向渠道。忽视社交媒体营销将影响与客户的关系。最重要的是,它将…...
飞行机器人专栏(十)-- 异构多视角视觉系统
感知系统架构为满足天空端主控制器的诸如RGB-D图像处理等大容量数据吞吐、高速并行计算、实时运动控制以及通信和可视化任务的计算算力需求,同时优化功耗表现,采用了结构紧凑、功耗表现优异的边缘计算硬件NVIDA IJetson AGXOrin 。该开发者套件包含高性能…...

2023年湖北住建厅八大员各岗位题库精准小题库-启程别
2023年湖北住建厅八大员各岗位题库精准小题库-启程别 住建厅八大员(施工员、质量员、资料员、材料员、机械员、标准员、劳务员) 各岗位题库分2种: 1.住建厅八大员报名之后会有培训任务,完成培训任务学习才能安排考试,…...

志愿者招募令|来!一起Build OceanBase第一次开发者大会
2023 年 3 月 25 日,我们将开启第一次 OceanBase 开发者大会,走近开发者,共同探讨单机分布式、云原生、HTAP 等数据库前沿趋势,分享全新的产品 Roadmap,交流场景探索和最佳实践。 为了让活动现场更有活力,…...

java 元数据 和 元注解
基本介绍三种基本注解OverrideDeprecatedSuppressWarnings四种元注解RetentionTargetDocumentedInherited一、基本介绍1.概述java注解(Annotation)[ˌ nəˈ teɪʃn],又称java标注,也被称为元数据(关于数据的数据&…...

RFID射频卡写入手机NFC心路小记
声明: 本文仅是作者学习探索的心里路程日记,如果您看完以后,从中获得了一些知识,作者不胜荣幸。科技是一把双刃剑,利用好了,可以方便生活,利用不当也肯能扰乱公共管理秩序,造成不必要…...

【C++】STL 模拟实现之 list
文章目录一、list 的常用接口及其使用1、list 一般接口2、list 特殊接口3、list 排序的性能分析二、list 迭代器的实现1、迭代器的分类2、list 迭代器失效问题3、list 迭代器源码分析4、list 迭代器模拟实现4.1 普通迭代器4.2 const 迭代器4.3 完整版迭代器三、list 的模拟实现…...

20230228----重返学习-数组-引用数据类型的转换-基础调试用方法-对象检测-各数据转布尔值及相等运算符-条件语句-循环语句
day-017-seventeen-20230228-数组-引用数据类型的转换-基础调试用方法-对象检测-各数据转布尔值及相等运算符-条件语句-循环语句 数组 字面量表示法 [数组成员0,数组成员1,数组成员2]用中括号语法来取值 var ary [5,6,7] console.log("ary[0]--->", ary[0])数组…...

apscheduler 定时任务框架
Apscheduler 介绍 四大组件 triggers:触发器,用于设定触发任务的条件job stores:作业存储器,用于存放任务,可以存放在数据库或内存,默认内存executors:执行器,用于执行任务&#x…...

Softing OPC Tunnel——绕过DCOM配置实现OPC Classic广域网通信
一 摘要 Softing OPC Tunnel是dataFEED OPC Suite的一个组件,可避免跨设备OPC Classic通信中出现的DCOM配置问题,同时可保证跨网络数据交换的高性能和可靠性。OPC Tunnel内部集成的存储转发功能,可在连接中断时缓存数据,并在重新…...

Python爬虫实战:研究feedparser库相关技术
1. 引言 1.1 研究背景与意义 在当今信息爆炸的时代,互联网上存在着海量的信息资源。RSS(Really Simple Syndication)作为一种标准化的信息聚合技术,被广泛用于网站内容的发布和订阅。通过 RSS,用户可以方便地获取网站更新的内容,而无需频繁访问各个网站。 然而,互联网…...

解锁数据库简洁之道:FastAPI与SQLModel实战指南
在构建现代Web应用程序时,与数据库的交互无疑是核心环节。虽然传统的数据库操作方式(如直接编写SQL语句与psycopg2交互)赋予了我们精细的控制权,但在面对日益复杂的业务逻辑和快速迭代的需求时,这种方式的开发效率和可…...

从深圳崛起的“机器之眼”:赴港乐动机器人的万亿赛道赶考路
进入2025年以来,尽管围绕人形机器人、具身智能等机器人赛道的质疑声不断,但全球市场热度依然高涨,入局者持续增加。 以国内市场为例,天眼查专业版数据显示,截至5月底,我国现存在业、存续状态的机器人相关企…...

关于 WASM:1. WASM 基础原理
一、WASM 简介 1.1 WebAssembly 是什么? WebAssembly(WASM) 是一种能在现代浏览器中高效运行的二进制指令格式,它不是传统的编程语言,而是一种 低级字节码格式,可由高级语言(如 C、C、Rust&am…...

企业如何增强终端安全?
在数字化转型加速的今天,企业的业务运行越来越依赖于终端设备。从员工的笔记本电脑、智能手机,到工厂里的物联网设备、智能传感器,这些终端构成了企业与外部世界连接的 “神经末梢”。然而,随着远程办公的常态化和设备接入的爆炸式…...

使用LangGraph和LangSmith构建多智能体人工智能系统
现在,通过组合几个较小的子智能体来创建一个强大的人工智能智能体正成为一种趋势。但这也带来了一些挑战,比如减少幻觉、管理对话流程、在测试期间留意智能体的工作方式、允许人工介入以及评估其性能。你需要进行大量的反复试验。 在这篇博客〔原作者&a…...

基于IDIG-GAN的小样本电机轴承故障诊断
目录 🔍 核心问题 一、IDIG-GAN模型原理 1. 整体架构 2. 核心创新点 (1) 梯度归一化(Gradient Normalization) (2) 判别器梯度间隙正则化(Discriminator Gradient Gap Regularization) (3) 自注意力机制(Self-Attention) 3. 完整损失函数 二…...

站群服务器的应用场景都有哪些?
站群服务器主要是为了多个网站的托管和管理所设计的,可以通过集中管理和高效资源的分配,来支持多个独立的网站同时运行,让每一个网站都可以分配到独立的IP地址,避免出现IP关联的风险,用户还可以通过控制面板进行管理功…...

day36-多路IO复用
一、基本概念 (服务器多客户端模型) 定义:单线程或单进程同时监测若干个文件描述符是否可以执行IO操作的能力 作用:应用程序通常需要处理来自多条事件流中的事件,比如我现在用的电脑,需要同时处理键盘鼠标…...

作为测试我们应该关注redis哪些方面
1、功能测试 数据结构操作:验证字符串、列表、哈希、集合和有序的基本操作是否正确 持久化:测试aof和aof持久化机制,确保数据在开启后正确恢复。 事务:检查事务的原子性和回滚机制。 发布订阅:确保消息正确传递。 2、性…...
