数据结构详细笔记——图
文章目录
- 图的定义
- 图的存储
- 邻接矩阵法
- 邻接表法
- 邻接矩阵法与邻接表法的区别
- 图的基本操作
- 图的遍历
- 广度优先遍历(BFS)
- 深度优先遍历(DFS)
- 图的遍历和图的连通性
图的定义
图G由顶点集V和边集E组成,记为G=(V,E),其中V(G)表示图G中顶点的有限非空集;E(G)表示图G中顶点之间的关系(边)集合,用|V|表示图G中顶点的个数,也称图G的阶,用|E|表示图G中边的条数
注意:线性表可以是空表,树可以是空树,但图不可以是空,即V一定是非空集
有向图
若E是有向边(也称弧)的有限集合时,则图G为有向图。弧是顶点的有序对,记为<v,w>,其中v、w是顶点,v称为弧尾,w称为弧头。<v,w> 不等于 <w,v>
无向图
若E是无向边(简称边)的有限集合时,则图G为无向图。边是顶点的有序对,记为(v,w)。(v,w) 等于 (w,v)
简单图
①不存在重复的边
②不存在顶点到自身的边
多重图
图G中某两个结点之间的边数多于一条,又允许顶点通过同一条边和自己关联
顶点的度、入读、出度
对于无向图:顶点v的度是指依附于该顶点的边的条数,记为TD(v)
对于有向图:
入度是以顶点v为终点的有向边的数目,记为ID(v)
出度是以顶点v为起点的有向边的数目,记为OD(v)
顶点v的度等于其入度和出度之和,即TD(v)=ID(v)+OD(v)
顶点-顶点的关系
- 路径——顶点到顶点之间的一条路径
- 回路——第一个顶点和最后一个顶点相同的路径称为回路或环
- 简单路径——在路径序列中,顶点不重复出现的路径称为简单路径
- 路径长度——路径上,边的数目
- 点到点的距离——从顶点u出发到顶点v的最短路径若存在,则此路径的长度称为从u到v的距离;若从u到v根本不存在路径,则该距离为无穷(∞)
- 无向图中,若从顶点v到顶点w有路径存在,则称v和w是连通的
- 有向图中,若从顶点v到顶点w和从顶点w到顶点v之间都有路径,则称这两个顶点是强连通的
连通图、强连通图
若图G中 任意两个顶点都是连通的,则称图G为 连通图,否则称为非连通图
对于n个顶点的无向图G
若G是连通图,则最少有 n-1 条边
若G是非连通图,则最多可能有条边
若图中 任何一对顶点都是强连通的,则称此图为 强连通图
对于n个顶点的有向图G
若G是强连通图,则最少有n条边(形成回路)
图的局部——子图
设有两个图G(V,E)和G’=(V’,E’),若V’是V的子集,且E’是E的子集,则称G‘是G的 子图
若有满足V(G’)=V(G)—— 顶点相同的子图G’,则称其为G的 生成子图
连通分量
无向图中的 极大连通子图(子图必须连通,且包含尽可能多的顶点和边)称为连通分量
强连通分量
有向图中的 极大强连通子图(子图必须连通,且包含尽可能多的顶点和边)称为强连通分量
生成树
连通图的生成树是包含图中全部顶点的一个极小连通子图
若图中顶点数为n,则它的生成树含有n-1条边,对生成树而言,若砍去它的一条边,则会变成非连通图,若加上一条边则会形成一个回路
生成森林
在非连通图中,连通分量的生成树构成了非连通图的生成森林
边的权、带权图/网
边的权——在一个图中,每条边都可以标上具有某种含义的数值,该数值称为该边的权值
带权图/网——边上带有权值的图称为带权图,也称网
带权路径长度——当图是带权图时,一条路径上所有边的权值之和,称为该路径的带权路径长度
几种特殊形态的图
无向完全图——无向图中任意两个顶点之间存在边
有向完全图——有向图中任意两个顶点之间都存在方向相反的两条弧
树——不存在回路,且连通的无向图
有向树——一个顶点的入度为0,其余顶点的入度均为1的有向图
总结
对于n个顶点的无向图G
所有顶点的度之和等于2|E|
若G是连通图,则最少有n-1条边(树),若 |E|>n-1,则一定有回路
若G是非连通图,则最多可能有条边
无向完全图共有条边
对于n个顶点的有向图G
所有顶点的出度之和=入度之和= |E|
所有顶点的度之和等于 2|E|
若G是强连接图,则最少有n条边(形成回路)
有向完全图共有条边
图的存储
邻接矩阵法
#define MaxVertexNum 100 // 顶点数目的最大值
typedef struct{char Vex[MaxVertexNum]; // 顶点表int Edge[MaxVertexNum][MaxVertexNum]; //邻接矩阵,边表int vexnum,arcnum; // 图的当前顶点数和边数/弧数
}MGraph;
邻接矩阵存储带权图
#define MaxVertexNum 100 // 顶点数量的最大值
#define INFINITY // 宏定义常量“无穷”
typedef char VertexType; // 顶点的数据类型
typedef int EdgeType; // 带权图中边上权值的数据类型
typedef struct{VertexType Vex[MaxVertexNum]; // 顶点EdgeType Edge[MaxVertexNum][MaxVertexNum]; // 边的权int vexnum,arcnum; // 图的当前顶点数和弧数
}MGraph;
空间复杂度
O(|V|²) ——只和顶点数相关,和实际的边数无关
适合于存储稠密图
无向图的邻接矩阵是对称矩阵,可以压缩存储(只存储上三角区/下三角区)
邻接矩阵法的性质
设图G的邻接矩阵为A(矩阵元素为0/1),则Aⁿ的元素Aⁿ[ i ][ j ]等于由顶点 i 到顶点 j 的长度为 n 的路径的数目
举个🌰:
A:
| A | B | C | D |
| A | 0 | 1 | 0 | 0 |
| B | 1 | 0 | 1 | 1 |
| C | 0 | 1 | 0 | 1 |
| D | 0 | 1 | 1 | 0 |
A² [ 1 ] [ 4 ] = a(1,1)a(1,4) + a(1,2)a(2,4) + a(1,3)a(3,4) + a(1,4)a(4,4) = 1
说明 顶点A到顶点D的长度为2的路径有1条
邻接表法
邻接表法——顺序+链式存储
// 边/弧
typedef struct ArcNode{int adjvex; // 边/弧指向哪个结点struct ArcNode *next; // 指向下一条弧的指针
}ArcNode;// 顶点
typedef struct VNode{VertexType data; // 顶点信息ArcNode *first; // 第一条边/弧
}VNode,AdjList[MaxVertexNum];// 用邻接表存储的图
typedef struct{AdjList vertices;int vexnum,arcnum;
}ALGraph;
无向图——边结点的数量是2|E|,整体空间复杂度为 O(|V|+2|E|)
有向图——边结点的数量是|E|,整体空间复杂度为 O(|V|+|E|)
邻接矩阵法与邻接表法的区别
| 邻接表 | 邻接矩阵 | |
|---|---|---|
| 空间复杂度 | 无向图:O(∣V∣+2∣E∣);有向图:O(∣V∣+∣E∣) | O(∣V∣²) |
| 适用于 | 存储稀疏图 | 存储稠密图 |
| 表示方式 | 不唯一 | 唯一 |
| 计算度/出度/入度 | 计算有向图的度、入度不方便,其余很方便 | 必须遍历对应行或列 |
| 找相邻的边 | 找有向图的入边不方便,其余很方便 | 必须遍历对应行或列 |
图的基本操作
-
Adjacent(G,x,y):判断图G是否存在边<x,y>或(x,y)
邻接矩阵————O(1)
邻接表 ————O(1)~O(|V|) -
Neighbors(G,x):列出图G中与结点x邻接的边
无向图:
邻接矩阵————O(|V|)
邻接表 ————O(1)~O(|V|)
有向图:
邻接矩阵————O(|V|)
邻接表 ————出度:O(1)~O(|V|);入度:O(|E|) -
InsertVertex(G,x):在图G中插入顶点x
邻接矩阵————O(1)
邻接表 ————O(1) -
DeleteVertex(G,x):在图G中删除顶点x
无向图:
邻接矩阵————O(|V|)
邻接表 ————O(1)~O(|V|)
有向图:
邻接矩阵————O(|V|)
邻接表 ————删出边:O(1)~O(|V|);删入边:O(|E|) -
AddEdge(G,x,y):若无向边(x,y)或有向边<x,y>不存在,则向图G中添加该边
邻接矩阵————O(1)
邻接表 ————O(1) -
FirstNeighbor(G,x):求图G中顶点x的第一个邻接点,若有则返回顶点号,若没有邻接点或图中不存在x,则返回-1
无向图:
邻接矩阵————O(1)~O(|V|)
邻接表 ————O(1)
有向图:
邻接矩阵————O(1)~O(|V|)
邻接表 ————找出边:O(1);找入边:O(1)~O(|E|) -
NextNeighbor(G,x,y):假设图G中顶点y是顶点x的一个邻接点,返回除y之外顶点x的下一个邻接点的顶点号,若y是x的最后一个邻接点,则返回-1
邻接矩阵————O(1)~O(|V|)
邻接表 ————O(1) -
Get_edge_value(G,x,y):获取图G中边(x,y)或<x,y>对应的权值
-
Set_edge_value(G,x,y):设置图G中边(x,y)或<x,y>对应的权值
图的遍历
广度优先遍历(BFS)
图的广度优先遍历和树的层次遍历很相似
代码实现:
bool visited[MAX_VERTEX_NUM]; // 访问标记数组// 广度优先遍历
void BFS(Graph G, int v){ // 从顶点v出发,广度优先遍历图Gvisit(v); // 访问初始顶点vvisited[v] = true; // 对v做已访问标记EnQueue(Q,v); // 顶点v入队列Qwhile(!isEmpty(Q)){DeQueue(Q,v); // 顶点v出队列for(w=FirstNeighbor(G,v);w>=0;w=NextNeighbor(G,v,w)){// 检测v所有邻接点if(!visited[w]){ // w为v的未访问的邻接顶点visit(w); // 访问顶点wvisited[w]=true; // 对w做已访问标记EnQueue(Q,w); // 顶点w入队列}}}
}如果是非连通图,则无法遍历完所有的结点,以上的代码就出现了Bug
所以先对所有的顶点遍历,还需要加上以下代码
void BfsTraverse(Graph G){for(i=0;i<G.vexnum;++i){visited[i]=false; // 访问标记数组}InitQueue(Q); // 初始化辅助队列Qfor(i=0;i<G.vexnum;++i){ // 从0号顶点开始遍历if(!visited[i]) // 对每一个连通分量调用依次BFSBFS(G,i); // vi未访问过,从vi开始BFS}
}
结论:对于无向图,调用BFS函数的次数=连通分量数
注意:
同一个图的邻接矩阵表示方式唯一,因此广度优先遍历序列唯一
同一个图的邻接表表示方式不唯一,因此广度优先遍历序列不唯一
复杂度分析
对于邻接矩阵存储的图:O(|v|²)
对于邻接表存储的图:O(|V|+|E|)
广度优先生成树
由广度优先遍历过程确定,将遍历过程中没有经过的边去掉
由于邻接表的表示方式不唯一,因此基于邻接表的广度优先生成树也不唯一
遍历非连通图可以得到广度优先生成森林
深度优先遍历(DFS)
图的深度优先遍历和树的先根遍历很相似
bool visited[MAX_VERTEX_NUM]; // 访问标记数组
void DFSTraverse(Graph G){for(v=0;v<G.vexnum;++v)visited[v]=false;for(v=0;v<G.vexnum;++v)if(!visited[v])DFS(G,v)
}void DFS(Graph G,int v){visit(v);visited[v]=true;for(w=FirstNeighbor(G,v);w>=0;w=NextNeighbor(G,v,w)){if(!visited[w]){DFS(G,w);}}
}
结论:对于无向图,调用D FS函数的次数=连通分量数
复杂度分析
空间复杂度:O(|v|)
对于邻接矩阵存储的图:O(|v|²)
对于邻接表存储的图:O(|V|+|E|)
深度优先遍历序列
注意:
同一个图的邻接矩阵表示方式唯一,因此深度优先遍历序列唯一
同一个图的邻接表表示方式不唯一,因此深度优先遍历序列不唯一
深度优先生成树
由深度优先遍历过程确定,将遍历过程中没有经过的边去掉
由于邻接表的表示方式不唯一,因此基于邻接表的深度优先生成树也不唯一
遍历非连通图可以得到深度优先生成森林
图的遍历和图的连通性
无向图:
DFS/BFS函数调用次数=连通分量数
有向图:
1、若从起始顶点到其他顶点都有路径,则只需要调用1次DFS/BFS函数
2、对于强连通图,从任一顶点出发都只需要调用1次DFS/BFS函数
相关文章:
数据结构详细笔记——图
文章目录 图的定义图的存储邻接矩阵法邻接表法邻接矩阵法与邻接表法的区别 图的基本操作图的遍历广度优先遍历(BFS)深度优先遍历(DFS)图的遍历和图的连通性 图的定义 图G由顶点集V和边集E组成,记为G(V,E),…...
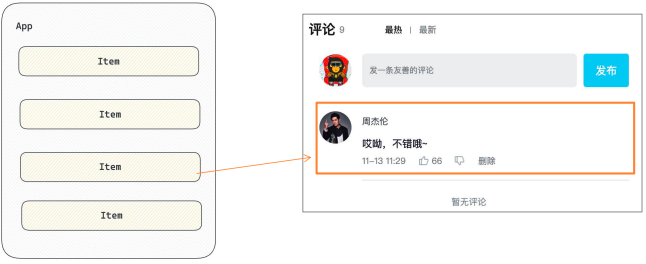
黑马React18: 基础Part II
黑马React: 基础2 Date: November 16, 2023 Sum: 受控表单绑定、获取DOM、组件通信、useEffect、Hook、优化B站评论 受控表单绑定 受控表单绑定 概念:使用React组件的状态(useState)控制表单的状态 准备一个React状态值 const [value, se…...
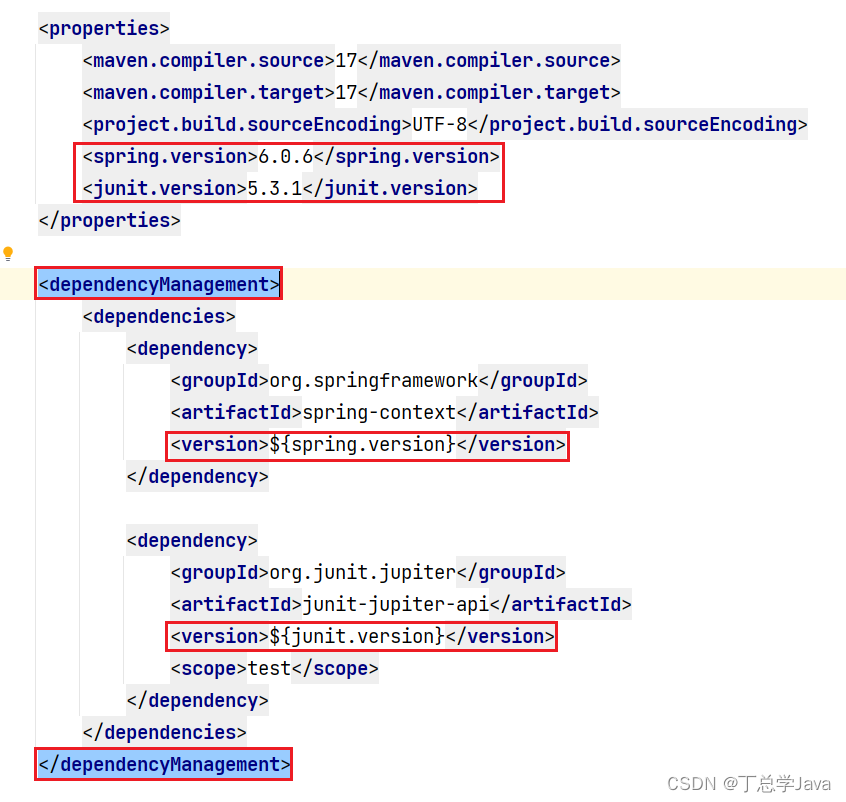
Maven工程继承关系,多个模块要使用同一个框架,它们应该是同一个版本,项目中使用的框架版本需要统一管理。
1、父工程pom.xml <?xml version"1.0" encoding"UTF-8"?> <project xmlns"http://maven.apache.org/POM/4.0.0"xmlns:xsi"http://www.w3.org/2001/XMLSchema-instance"xsi:schemaLocation"http://maven.apache.org/PO…...
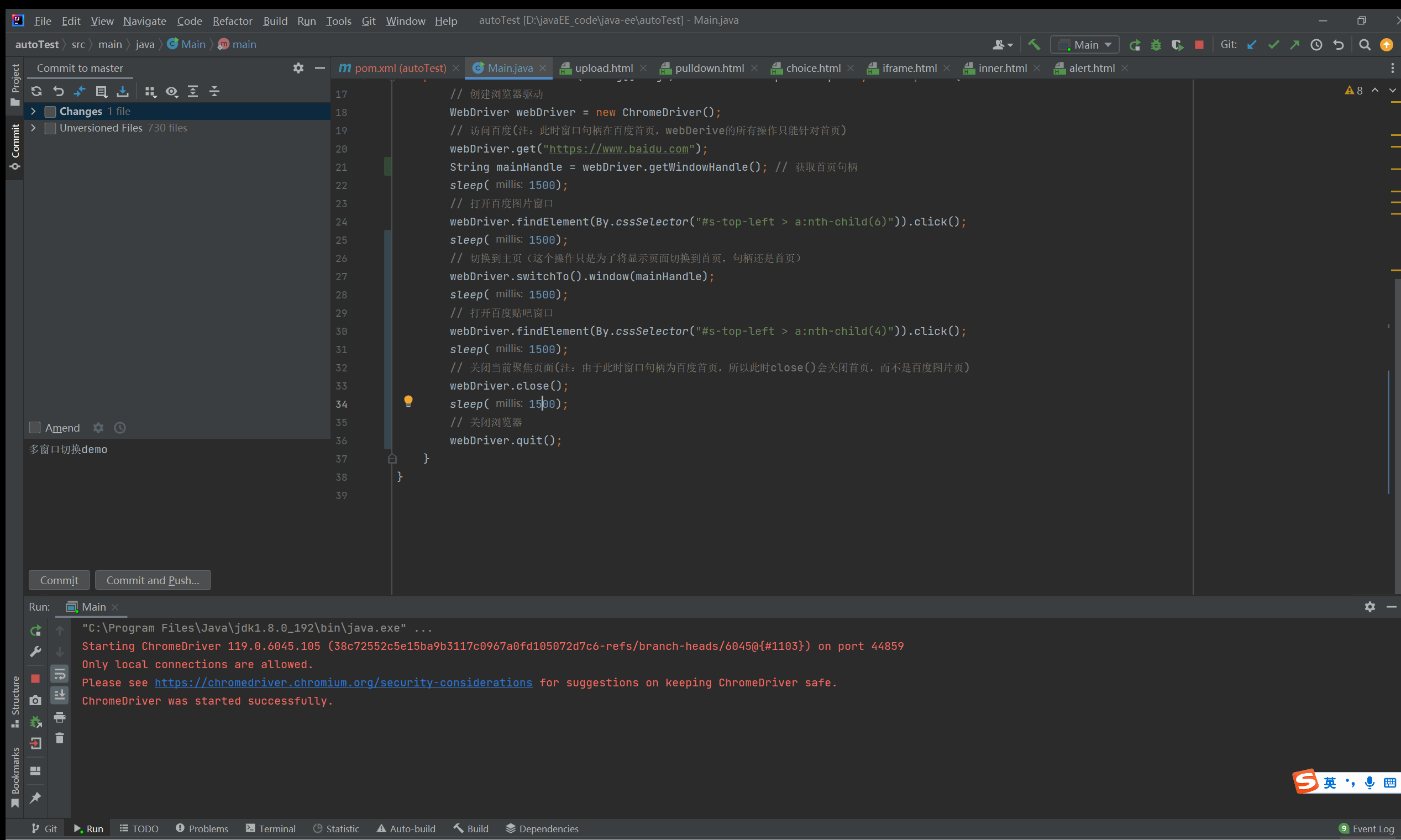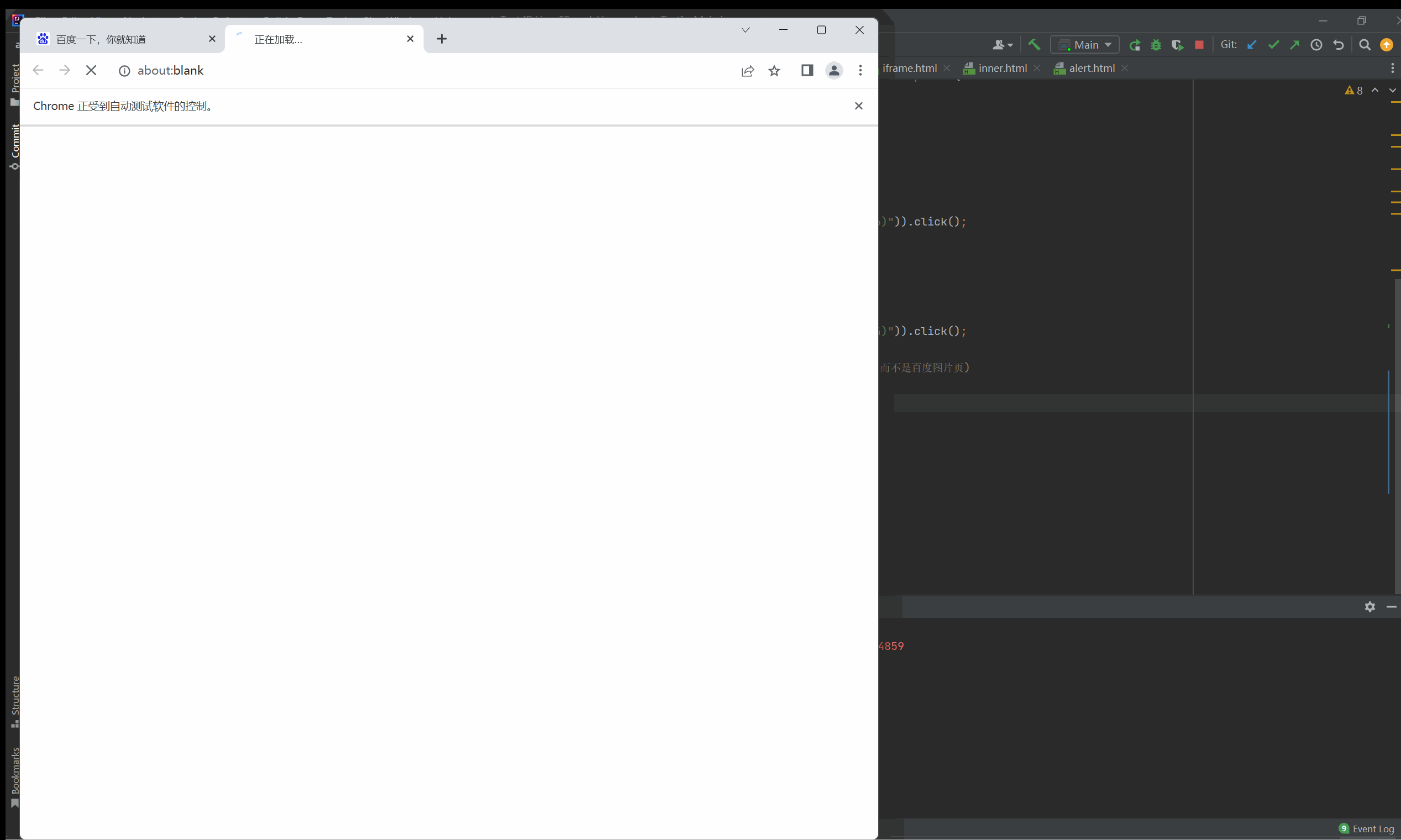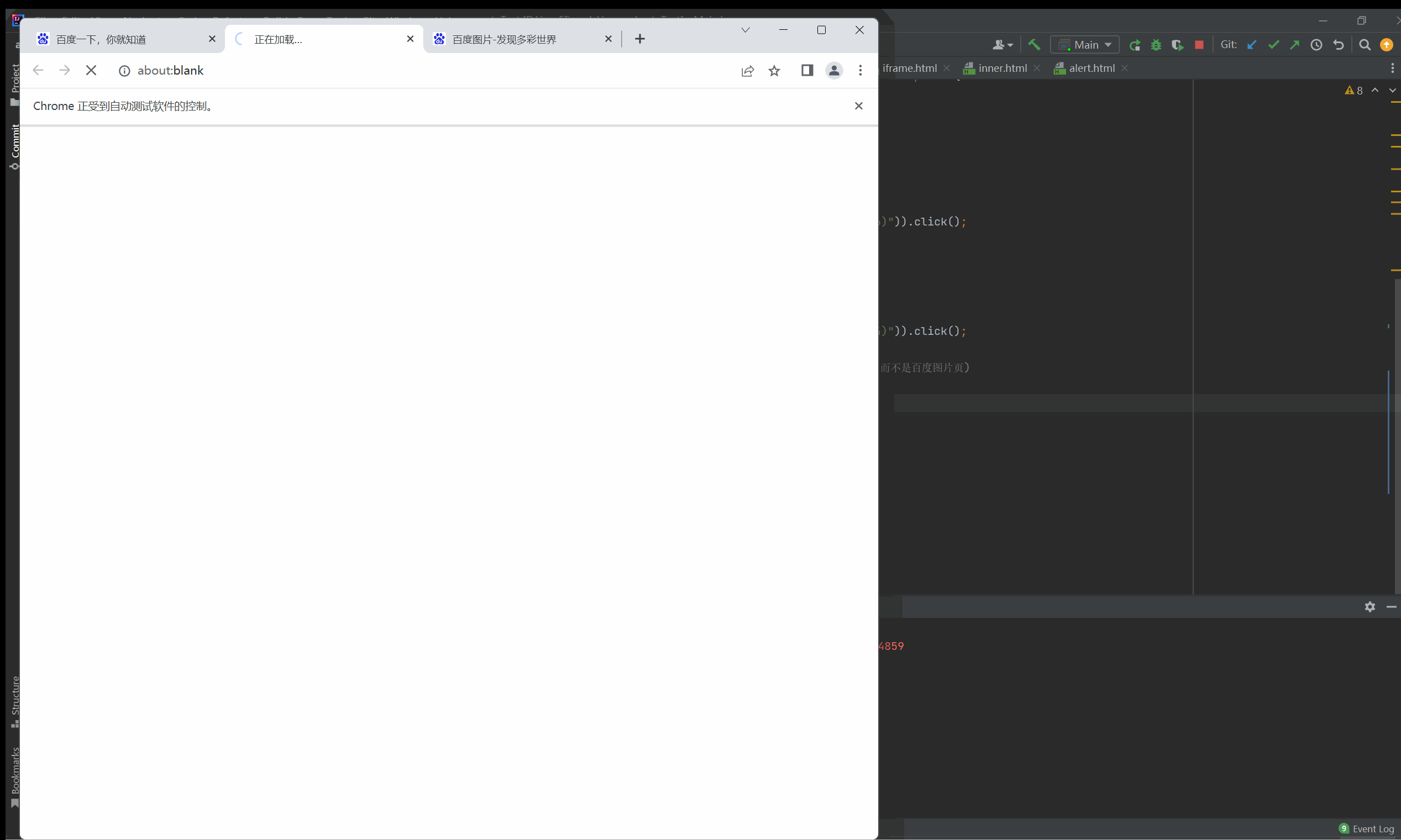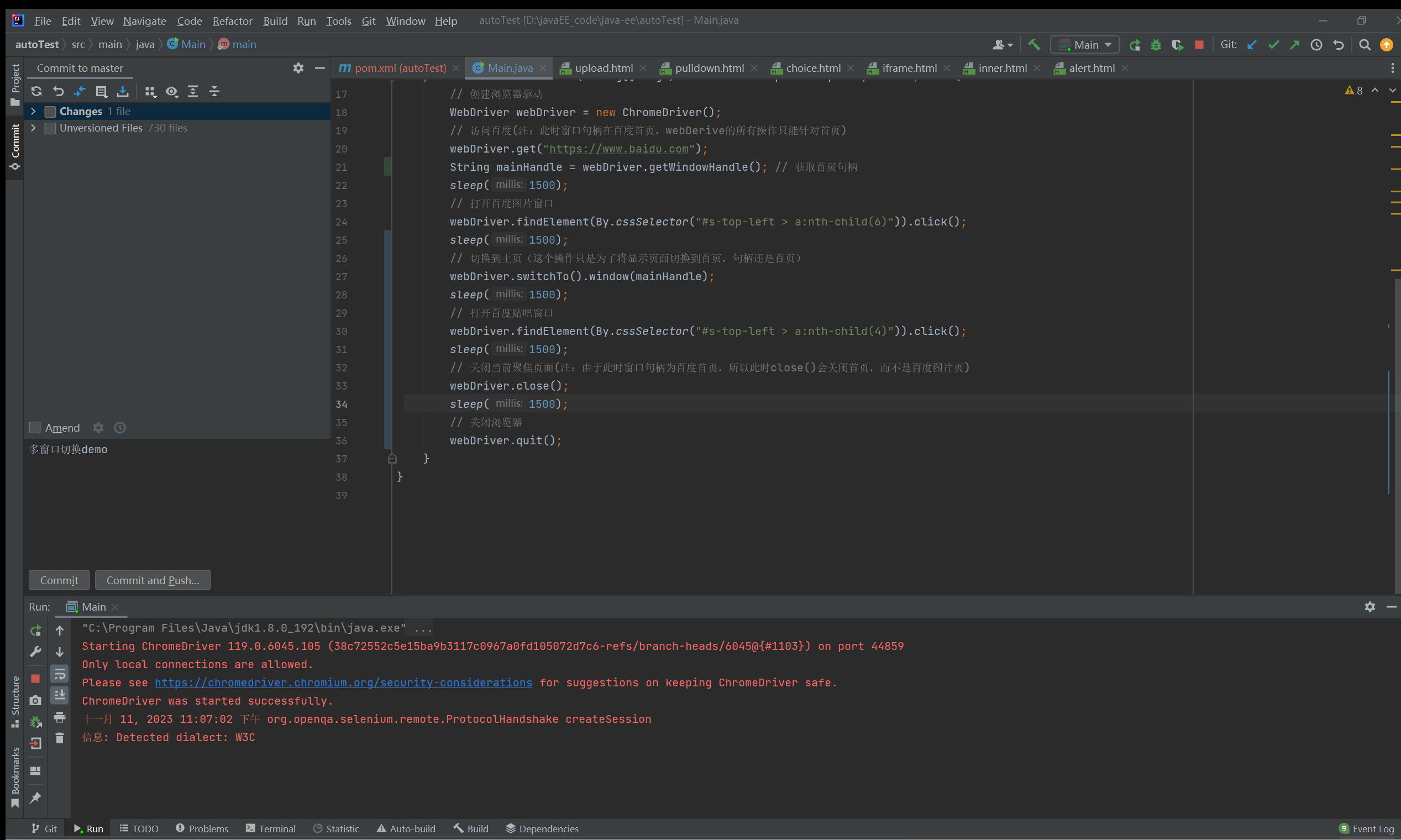
Selenium UI 自动化
一、Selenium 自动化 1、什么是Selenium? Selenium是web应用中基于UI的自动化测试框架。 2、Selenium的特点? 支持多平台、多浏览器、多语言。 3、自动化工作原理? 通过上图,我们可以注意到3个角色,下面具体讲解一…...

竞赛 题目:基于深度学习的图像风格迁移 - [ 卷积神经网络 机器视觉 ]
文章目录 0 简介1 VGG网络2 风格迁移3 内容损失4 风格损失5 主代码实现6 迁移模型实现7 效果展示8 最后 0 简介 🔥 优质竞赛项目系列,今天要分享的是 基于深度学习卷积神经网络的花卉识别 该项目较为新颖,适合作为竞赛课题方向,…...
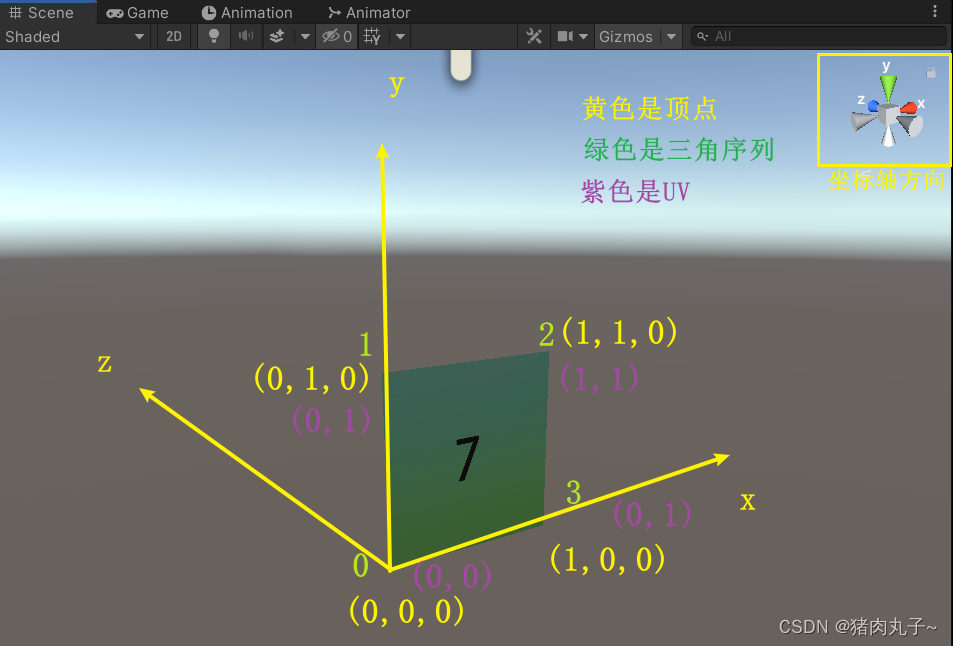
【unity3D-网格编程】01:Mesh基础属性以及用代码创建一个三角形
💗 未来的游戏开发程序媛,现在的努力学习菜鸡 💦本专栏是我关于游戏开发的网格编程方面学习笔记 🈶本篇是unity的网格编程系列01-mesh基础属性 网格编程系列01 mesh基础属性实践操作用代码初始化一个三角形在三角形的基础上改成正…...
Java贪吃蛇小游戏
Java贪吃蛇小游戏 import javax.swing.*; import java.awt.*; import java.awt.event.ActionEvent; import java.awt.event.ActionListener; import java.awt.event.KeyEvent; import java.awt.event.KeyListener; import java.util.LinkedList; import java.util.Random;publi…...
)
Linux:系统基本信息扫描(1)
#系统基本信息: uname -a #Linux发行版信息: lsb_release -a #内核与发行版信息: cat /proc/version #linux 用户 cat /etc/passwd #Linux 组查询 cat /etc/group #CPU详细信息:lscpu -a #获取CPU模式: cat /sys/devices/system/cpu/cpu0/cpufreq/scaling\_governor #per…...

VR全景打造亮眼吸睛创意内容:三维模型、实景建模
随着VR技术在不同行业之间应用落地,市场规模也在快速扩大,VR全景这种全新的视觉体验为我们生活中的许多方面都带来了无限的可能。更加完整的呈现出一个场景或是物体的所有细节,让浏览者感受到自己仿佛置身于现场一般;其次…...
ProTable高级表格获取表单数据
隐藏高级表格中的收起按钮 手动控制高级表格中的搜索按钮 获取高级表格中的表单数据 Forminstance 引入 然后在代码中定义 const refForm useRef(); 使用 refForm.current.getFileDsValue();...

力扣刷题第二十七天--二叉树
前言 题目大同小异,按要求来即可。 内容 一、二叉树的右视图 199.二叉树的右视图 给定一个二叉树的 根节点 root,想象自己站在它的右侧,按照从顶部到底部的顺序,返回从右侧所能看到的节点值。 广度优先搜索 取每层最后一个…...

一个快递包裹的跨国之旅
事情要从今年三月份说起,一位爱尔兰的同事在6月份结婚,团队同事准备了中国风的丝绸画轴、领带、丝巾作为礼物。3月份开始邮寄,4月初爱尔兰方面收件,5月份因为文件不足、不完整、不正确等原因被取消进口,7月份退回到大连…...

qsort函数使用方法总结
目录 一、qsort函数原型 二、compar参数 三、各种类型的qsort排序 1. int 数组排序 2. 结构体排序 3. 字符串指针数组排序 4. 字符串二维数组排序 四、回调函数 1. 什么是回调函数 2. 为什么要用回调函数? 3. 怎么使用回调函数? 4.下面是…...

机器学习介绍与分类
随着科学技术的不断发展,机器学习作为人工智能领域的重要分支,正逐渐引起广泛的关注和应用。本文将介绍机器学习的基本概念、原理和分类方法,帮助读者更好地理解和应用机器学习技术。 一、机器学习的基本概念 机器学习是一种通过从数据中学…...

linux控制台命令
进入root sudo su root 浏览当前文件夹列表 ll ls 查看文件 vim test.txt :q 退出查看模式 上传 sudo rz rz 覆盖上传 rz -y 修改文件名: mv 旧文件名 新文件名 修改文件权限 sudo chmod ar xxx.txt sudo chmod 777 test.txt 7 4 2 1 读写运行权限…...
快时尚品牌Halara登上TikTok美国小店榜Top 5,运动健身风靡TikTok
TikTok Shop美国电商数据周榜(11/06-12)已出,具体信息如下: 上周总GMV达到5850万美元,日均出单840万美元;单日出单最高达2110万美元,是当前美国单日最高销售额; 截至11月12日&…...

Docker 安装 Oracle Database 23c
目录 访问 Oracle 官方网站 使用 Docker 运行 Oracle Database 23c 免费容器映像 创建并运行 Oracle Database 23c 容器 查看已下载的镜像 列出正在运行的容器 进入容器 sqlplus 命令 访问 Oracle 官方网站 Database Software Downloads | Oracle 中国 使用 Docker 运行…...

什么是美国服务器,有哪些优势,适用于什么场景?
在互联网发展的过程中,服务器扮演着至关重要的角色。而美国作为全球信息技术的中心,其服务器在全球范围内受到广泛关注。 美国服务器是指在美国本土机房搭建并运行的服务器。其拥有带宽大、优质硬件、售后运维好、位置优越、数据安全性高以及免备…...

TeXLive 2023安装教程
TeXLive 2023安装教程 本文介绍最新TeX发行版——TeXLive 2023的安装步骤。如果你想用LaTeX进行写作,那么需要搭建LaTeX环境:可以选择下面两种方案之一进行安装:(1)TeXLive 2023TeXStudio或者(2)TeXLive 2023WinEdt 11。其中TeXLive 2023是由…...

uniapp中swiper 轮播带左右箭头,点击切换轮播效果demo(整理)
可以点击箭头左右切换-进行轮播 <template><view class"swiper-container"><swiper class"swiper" :current"currentIndex" :autoplay"true" interval"9000" circular indicator-dotschange"handleSw…...

stm32G473的flash模式是单bank还是双bank?
今天突然有人stm32G473的flash模式是单bank还是双bank?由于时间太久,我真忘记了。搜搜发现,还真有人和我一样。见下面的链接:https://shequ.stmicroelectronics.cn/forum.php?modviewthread&tid644563 根据STM32G4系列参考手…...

相机Camera日志实例分析之二:相机Camx【专业模式开启直方图拍照】单帧流程日志详解
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了: 这一篇我们开始讲: 目录 一、场景操作步骤 二、日志基础关键字分级如下 三、场景日志如下: 一、场景操作步骤 操作步…...

从深圳崛起的“机器之眼”:赴港乐动机器人的万亿赛道赶考路
进入2025年以来,尽管围绕人形机器人、具身智能等机器人赛道的质疑声不断,但全球市场热度依然高涨,入局者持续增加。 以国内市场为例,天眼查专业版数据显示,截至5月底,我国现存在业、存续状态的机器人相关企…...

2024年赣州旅游投资集团社会招聘笔试真
2024年赣州旅游投资集团社会招聘笔试真 题 ( 满 分 1 0 0 分 时 间 1 2 0 分 钟 ) 一、单选题(每题只有一个正确答案,答错、不答或多答均不得分) 1.纪要的特点不包括()。 A.概括重点 B.指导传达 C. 客观纪实 D.有言必录 【答案】: D 2.1864年,()预言了电磁波的存在,并指出…...

HTML 列表、表格、表单
1 列表标签 作用:布局内容排列整齐的区域 列表分类:无序列表、有序列表、定义列表。 例如: 1.1 无序列表 标签:ul 嵌套 li,ul是无序列表,li是列表条目。 注意事项: ul 标签里面只能包裹 li…...

Neo4j 集群管理:原理、技术与最佳实践深度解析
Neo4j 的集群技术是其企业级高可用性、可扩展性和容错能力的核心。通过深入分析官方文档,本文将系统阐述其集群管理的核心原理、关键技术、实用技巧和行业最佳实践。 Neo4j 的 Causal Clustering 架构提供了一个强大而灵活的基石,用于构建高可用、可扩展且一致的图数据库服务…...

【JavaSE】绘图与事件入门学习笔记
-Java绘图坐标体系 坐标体系-介绍 坐标原点位于左上角,以像素为单位。 在Java坐标系中,第一个是x坐标,表示当前位置为水平方向,距离坐标原点x个像素;第二个是y坐标,表示当前位置为垂直方向,距离坐标原点y个像素。 坐标体系-像素 …...

大学生职业发展与就业创业指导教学评价
这里是引用 作为软工2203/2204班的学生,我们非常感谢您在《大学生职业发展与就业创业指导》课程中的悉心教导。这门课程对我们即将面临实习和就业的工科学生来说至关重要,而您认真负责的教学态度,让课程的每一部分都充满了实用价值。 尤其让我…...

PostgreSQL——环境搭建
一、Linux # 安装 PostgreSQL 15 仓库 sudo dnf install -y https://download.postgresql.org/pub/repos/yum/reporpms/EL-$(rpm -E %{rhel})-x86_64/pgdg-redhat-repo-latest.noarch.rpm# 安装之前先确认是否已经存在PostgreSQL rpm -qa | grep postgres# 如果存在࿰…...

永磁同步电机无速度算法--基于卡尔曼滤波器的滑模观测器
一、原理介绍 传统滑模观测器采用如下结构: 传统SMO中LPF会带来相位延迟和幅值衰减,并且需要额外的相位补偿。 采用扩展卡尔曼滤波器代替常用低通滤波器(LPF),可以去除高次谐波,并且不用相位补偿就可以获得一个误差较小的转子位…...
