泉盛UV-K5/K6全功能中文固件
https://github.com/wu58430/uv-k5-firmware-chinese/releases
主要功能:
-
中文菜单
-
许多来自 OneOfEleven 的模块:
- AM 修复,显著提高接收质量
- 长按按钮执行
F+操作的功能复制 - 快速扫描
- 菜单中的频道名称编辑
- 频道名称 + 频率显示选项
- 扫描列表分配的快捷方式(长按
5 NOAA) - 扫描时的扫描列表切换(在扫描时长按
* Scan) - 从菜单中可选择的可配置按钮功能
- 状态栏上的电池百分比/电压,可从菜单中选择
- 更长的背光时间
- 麦克风条
- 信号强度指示器(RSSI s-meter)
- 更多的频率步进
- 静噪更为敏感
-
fagci 频谱分析仪(F+5 打开)
-

-

相关文章:

泉盛UV-K5/K6全功能中文固件
https://github.com/wu58430/uv-k5-firmware-chinese/releases 主要功能: 中文菜单 许多来自 OneOfEleven 的模块: AM 修复,显著提高接收质量长按按钮执行 F 操作的功能复制快速扫描菜单中的频道名称编辑频道名称 频率显示选项扫描列表分配…...

基于JPBC的无证书聚合签名方案实现
基于JPBC的无证书聚合签名方案实现 摘要 一开始签名方案是基于PKI的,无证书签名起源于 基于身份密码体制, 2009 年第一篇无证书签名方案1被提出,随后出现了一些列方案2,3;包括无配对的无证书聚合签名方案4,更多内容参考文献5. 暂时没有看见…...
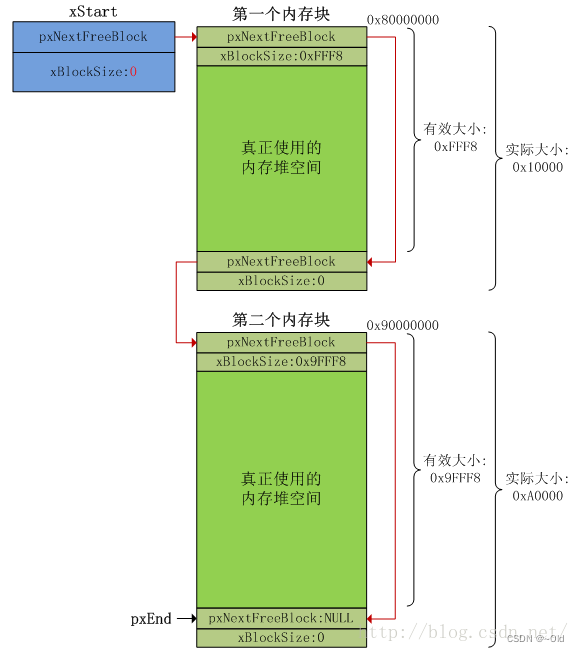
FreeRTOS内存管理分析
目录 heap_1.c内存管理算法 heap_2.c内存管理算法 heap_3.c内存管理算法 heap_4.c内存管理算法 heap_5.c内存管理算法 内存管理对应用程序和操作系统来说非常重要,而内存对于嵌入式系统来说是寸土寸金的资源,FreeRTOS操作系统将内核与内存管理分开实…...

hashMap索引原理
平日里面经常使用map这种数据结构,令人称奇的是他的访问速度为什么那么快?为什么可以通过key以接近O(1)的速度查找? 一、基础数据结构特点分析 1.1数组 查找的时间复杂度为O(1) 插入时间复杂度为O(n) 1.2链表 查找的时间复杂度为O(n) 插…...

qcow2、raw、vmdk等镜像格式工具
如果没有qemu,可以从这里下载安装:https://qemu.weilnetz.de/w64/...
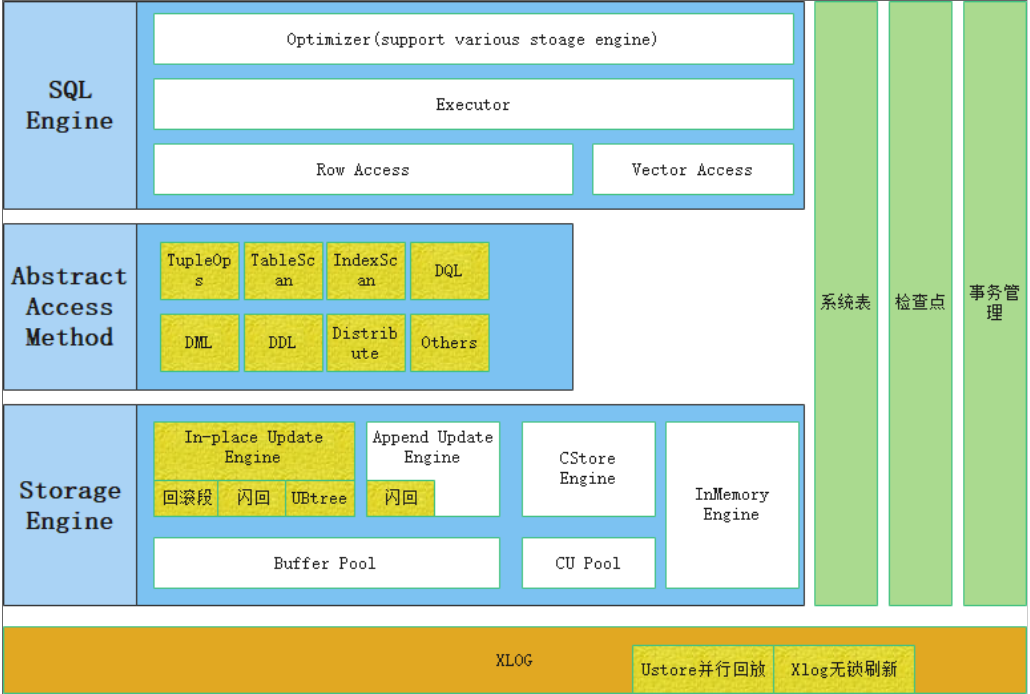
GaussDB新特性Ustore存储引擎介绍
1、 Ustore和Astore存储引擎介绍 Ustore存储引擎,又名In-place Update存储引擎(原地更新),是openGauss 内核新增的一种存储模式。此前的版本使用的行存储引擎是Append Update(追加更新)模式。相比于Append…...
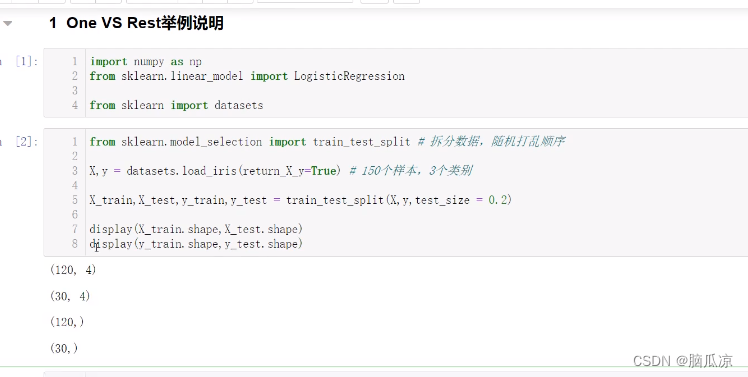
人工智能基础_机器学习046_OVR模型多分类器的使用_逻辑回归OVR建模与概率预测---人工智能工作笔记0086
首先我们来看一下什么是OVR分类.我们知道sigmoid函数可以用来进行二分类,那么多分类怎么实现呢?其中一个方法就是使用OVR进行把多分类转换成二分类进行计算. OVR,全称One-vs-Rest,是一种将多分类问题转化为多个二分类子问题的策略。在这种策略中,多分类问题被分解为若干个二…...
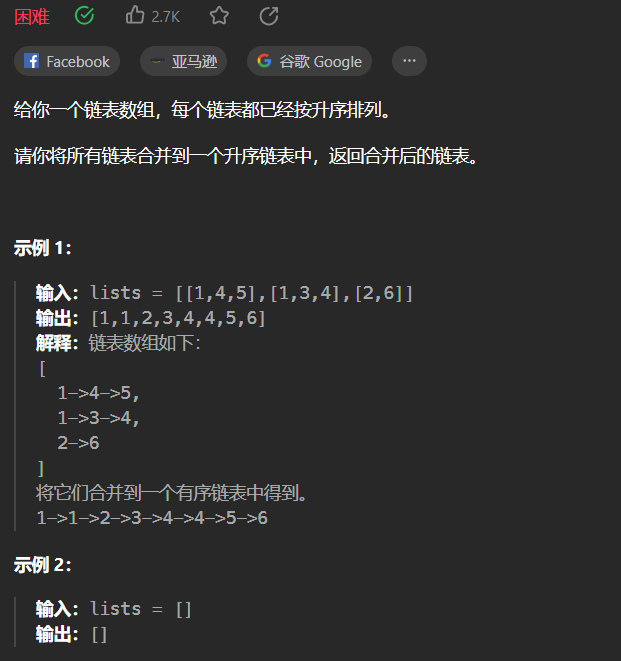
【LeetCode刷题-链表】--23.合并K个升序链表
23.合并K个升序链表 方法:顺序合并 在前面已经知道合并两个升序链表的前提下,用一个变量ans来维护以及合并的链表,第i次循环把第i个链表和ans合并,答案保存到ans中 /*** Definition for singly-linked list.* public class List…...

强化学习笔记
这里写自定义目录标题 参考资料基础知识16.3 有模型学习16.3.1 策略评估16.3.2 策略改进16.3.3 策略迭代16.3.3 值迭代 16.4 免模型学习16.4.1 蒙特卡罗强化学习16.4.2 时序差分学习Sarsa算法:同策略算法(on-policy):行为策略是目…...

经典双指针算法试题(一)
📘北尘_:个人主页 🌎个人专栏:《Linux操作系统》《经典算法试题 》《C》 《数据结构与算法》 ☀️走在路上,不忘来时的初心 文章目录 一、移动零1、题目讲解2、讲解算法原理3、代码实现 二、复写零1、题目讲解2、讲解算法原理3、…...
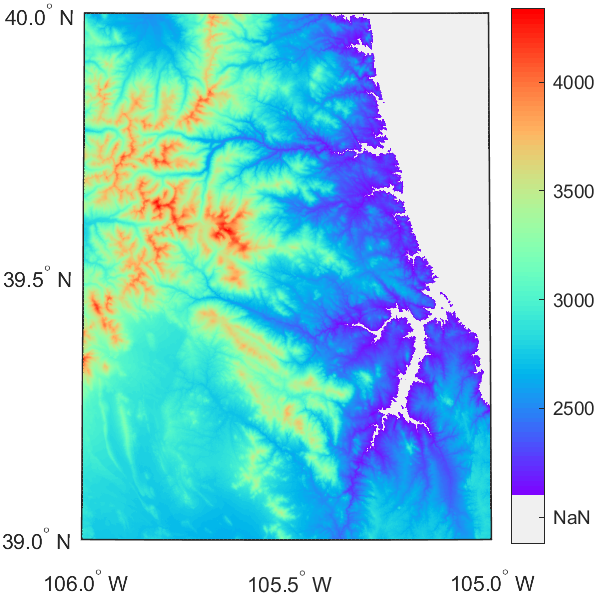
MATLAB | 绘图复刻(十三) | 带NaN图例的地图绘制
有粉丝问我地图绘制如何添加NaN,大概像这样: 或者这样: 直接上干货: 原始绘图 假设我们有这样的一张图地图,注意运行本文代码需要去matlab官网下载Mapping Toolbox工具箱,但是其实原理都是相似的&…...

netty整合websocket(完美教程)
websocket的介绍: WebSocket是一种在网络通信中的协议,它是独立于HTTP协议的。该协议基于TCP/IP协议,可以提供双向通讯并保有状态。这意味着客户端和服务器可以进行实时响应,并且这种响应是双向的。WebSocket协议端口通常是80&am…...

选择PC示波器的10种理由!
PC示波器(PCs)在测试仪器领域中的关键项目上正迅速地取代传统的数字存储示波器(DSOs),其中有十个理由: 小巧和便携示波器利用你的PC显示器实现大屏幕和精细彩色显示信号存储只受限于你的PC存储器大小捕捉波…...
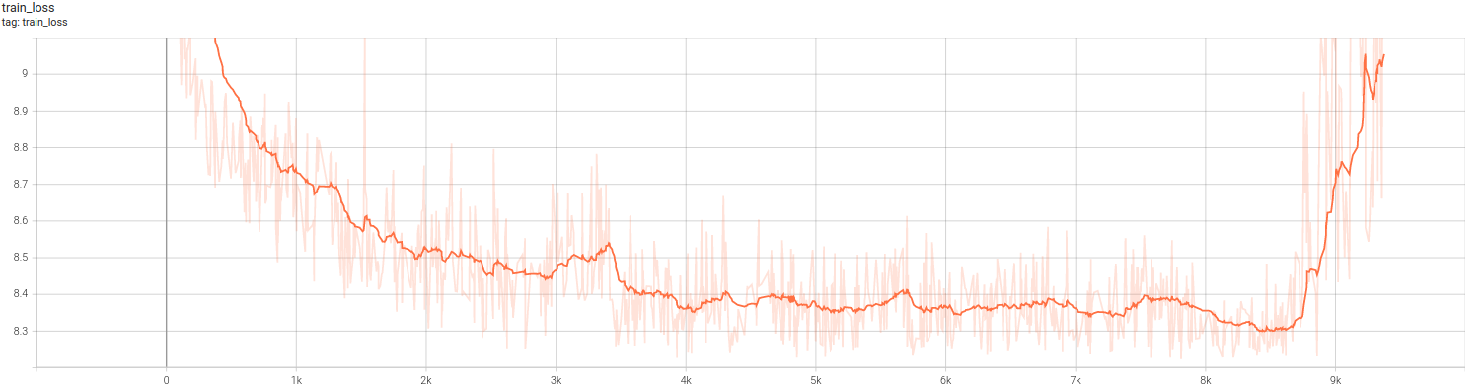
【pytorch深度学习 应用篇02】训练中loss图的解读,训练中的问题与经验汇总
文章目录 loss图解析train loss ↘ \searrow ↘ ↗ \nearrow ↗ 先降后升 loss图解析 train loss ↘ \searrow ↘ 不断下降,test loss ↗ \nearrow ↗ 不断上升:原因很多,我是把workers1,batchSize8192train loss ↘ \searro…...

uniapp 微信小程序如何实现多个item列表的分享
以下代码是某个循环里面的item <button class"cu-btn" style"background-color: transparent;padding: 0;"open-type"share" :data-tree"item.treeId" :data-project"item.projectId"v-if"typeId1 && userI…...
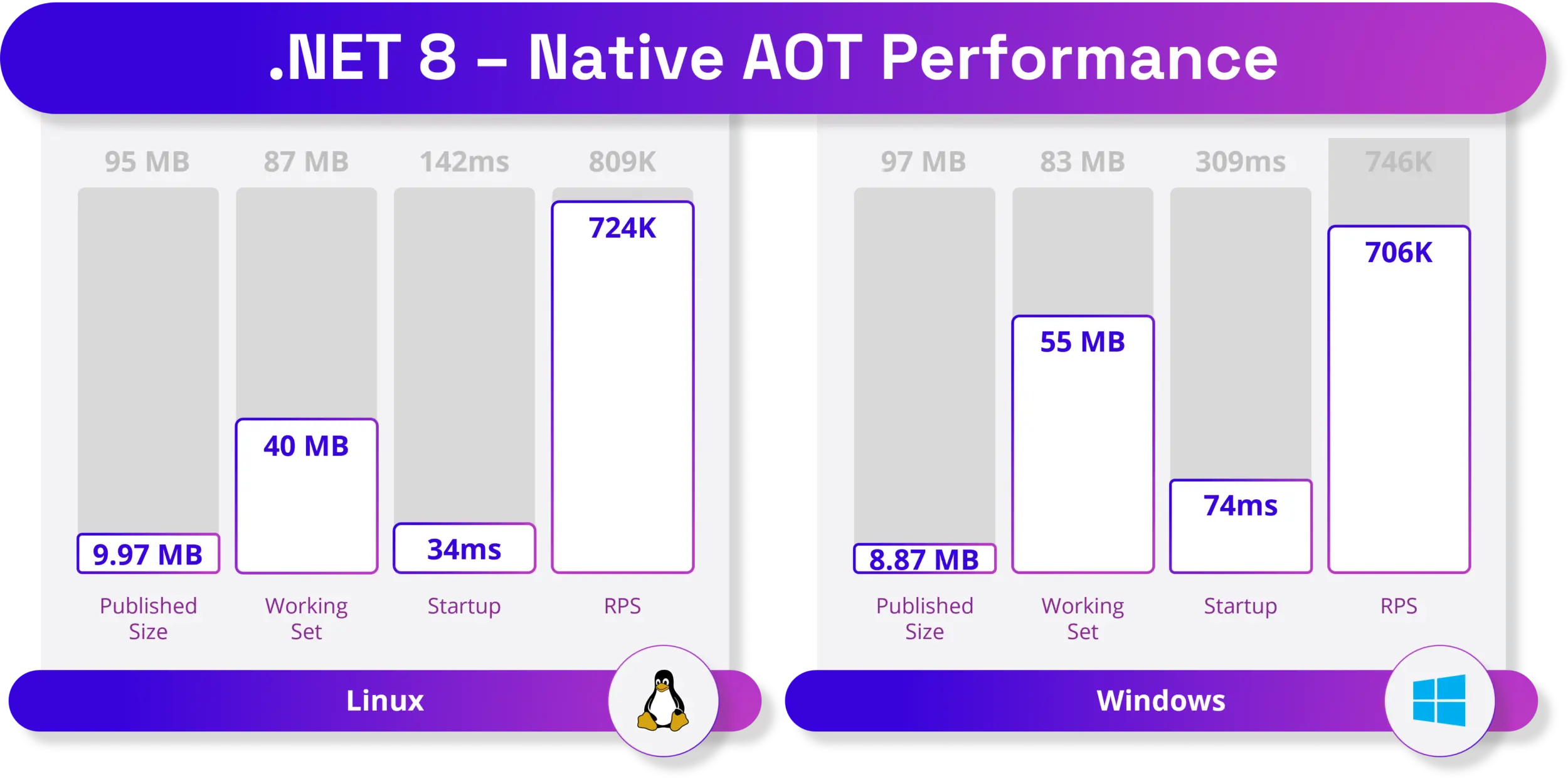
.NET 8 正式 GA 遥遥领先
.NET 8 一正式 已正式 GA。 微软称 .NET 8 提供了数以千计的性能、稳定性和安全性改进,以及平台和工具增强功能,有助于提高开发者的工作效率和创新速度。 比如 .NET 8 为 Android 和 WASM 引入了全新的 AOT 模式、改进 System.Text.Json,以…...

2216. 美化数组的最少删除数 --力扣 --JAVA
题目 给你一个下标从 0 开始的整数数组 nums ,如果满足下述条件,则认为数组 nums 是一个 美丽数组 : nums.length 为偶数对所有满足 i % 2 0 的下标 i ,nums[i] ! nums[i 1] 均成立 注意,空数组同样认为是美丽数组。…...

DDD 领域驱动设计
文章目录 请解释下什么是 DDD 领域驱动设计DDD 的四层领域模型是怎样的?包含哪些基础概念?DDD 中的贫血模型和充血模型有什么区别在 DDD 中,如何处理模型的聚合和聚合根DDD 中的实体和值对象有什么区别?在 DDD 中,如何…...
转型做视频了,博客就是稿子,继续坚持写博客,同时发布视频,能写博客说明思路清晰了,能再讲明白,理解就更透彻了,紧跟上时代发展。
1,今天特别记录下,B站给开通了《合集》功能 最近使用视频制作了几个视频。播放量还不错,最好的已经到了 2.6K了。 然后粉丝也涨到了 200个。 添加链接描述 紧跟时代:从写博客到录视频,粉丝大涨,突破200个&…...

小众市场:探索跨境电商中的利基领域
随着全球数字化和互联网的普及,跨境电子商务已经成为了一个蓬勃发展的产业。从亚马逊到阿里巴巴,大型电商平台已经占据了很大一部分市场份额。 然而,在这个竞争激烈的领域,寻找小众市场和利基领域可能是一种成功的策略。本文将探…...

React 第五十五节 Router 中 useAsyncError的使用详解
前言 useAsyncError 是 React Router v6.4 引入的一个钩子,用于处理异步操作(如数据加载)中的错误。下面我将详细解释其用途并提供代码示例。 一、useAsyncError 用途 处理异步错误:捕获在 loader 或 action 中发生的异步错误替…...

盘古信息PCB行业解决方案:以全域场景重构,激活智造新未来
一、破局:PCB行业的时代之问 在数字经济蓬勃发展的浪潮中,PCB(印制电路板)作为 “电子产品之母”,其重要性愈发凸显。随着 5G、人工智能等新兴技术的加速渗透,PCB行业面临着前所未有的挑战与机遇。产品迭代…...

Vue3 + Element Plus + TypeScript中el-transfer穿梭框组件使用详解及示例
使用详解 Element Plus 的 el-transfer 组件是一个强大的穿梭框组件,常用于在两个集合之间进行数据转移,如权限分配、数据选择等场景。下面我将详细介绍其用法并提供一个完整示例。 核心特性与用法 基本属性 v-model:绑定右侧列表的值&…...

Auto-Coder使用GPT-4o完成:在用TabPFN这个模型构建一个预测未来3天涨跌的分类任务
通过akshare库,获取股票数据,并生成TabPFN这个模型 可以识别、处理的格式,写一个完整的预处理示例,并构建一个预测未来 3 天股价涨跌的分类任务 用TabPFN这个模型构建一个预测未来 3 天股价涨跌的分类任务,进行预测并输…...

五年级数学知识边界总结思考-下册
目录 一、背景二、过程1.观察物体小学五年级下册“观察物体”知识点详解:由来、作用与意义**一、知识点核心内容****二、知识点的由来:从生活实践到数学抽象****三、知识的作用:解决实际问题的工具****四、学习的意义:培养核心素养…...

在WSL2的Ubuntu镜像中安装Docker
Docker官网链接: https://docs.docker.com/engine/install/ubuntu/ 1、运行以下命令卸载所有冲突的软件包: for pkg in docker.io docker-doc docker-compose docker-compose-v2 podman-docker containerd runc; do sudo apt-get remove $pkg; done2、设置Docker…...

PAN/FPN
import torch import torch.nn as nn import torch.nn.functional as F import mathclass LowResQueryHighResKVAttention(nn.Module):"""方案 1: 低分辨率特征 (Query) 查询高分辨率特征 (Key, Value).输出分辨率与低分辨率输入相同。"""def __…...

学习一下用鸿蒙DevEco Studio HarmonyOS5实现百度地图
在鸿蒙(HarmonyOS5)中集成百度地图,可以通过以下步骤和技术方案实现。结合鸿蒙的分布式能力和百度地图的API,可以构建跨设备的定位、导航和地图展示功能。 1. 鸿蒙环境准备 开发工具:下载安装 De…...

Unity中的transform.up
2025年6月8日,周日下午 在Unity中,transform.up是Transform组件的一个属性,表示游戏对象在世界空间中的“上”方向(Y轴正方向),且会随对象旋转动态变化。以下是关键点解析: 基本定义 transfor…...

6.9-QT模拟计算器
源码: 头文件: widget.h #ifndef WIDGET_H #define WIDGET_H#include <QWidget> #include <QMouseEvent>QT_BEGIN_NAMESPACE namespace Ui { class Widget; } QT_END_NAMESPACEclass Widget : public QWidget {Q_OBJECTpublic:Widget(QWidget *parent nullptr);…...
