【C++进阶之路】第五篇:哈希
文章目录
- 一、unordered系列关联式容器
- 1.unordered_map
- (1)unordered_map的介绍
- (2)unordered_map的接口说明
- 2. unordered_set
- 3.性能对比
- 二、底层结构
- 1.哈希概念
- 2.哈希冲突
- 3.哈希函数
- 4.哈希冲突解决
- (1)闭散列(开放地址法)
- (2)开散列(哈希桶/开链法 - 常用)
- 三、模拟实现
- 四、哈希的应用
- 1.位图
- (1)位图概念
- (2)位图的实现
- (3)位图的应用
- 2.布隆过滤器
- (1)布隆过滤器的提出
- (2)布隆过滤器概念
- (3)布隆函数的插入
- (4)布隆过滤器的查找(重点)
- (5)布隆过滤器的删除
- (6)布隆过滤器的优点
- (7)布隆过滤器的缺陷
- 五、海量数据面试题
- 1.哈希切割
- 2.位图应用
- 3.布隆过滤器
一、unordered系列关联式容器
在C++98中,STL提供了底层为红黑树结构的一系列关联式容器,在查询时效率可达到 l o g 2 N log_2 N log2N,即最差情况下需要比较红黑树的高度次,当树中的节点非常多时,查询效率也不理想。最好的查询是,进行很少的比较次数就能够将元素找到,因此在C++11中,STL又提供了4个unordered系列的关联式容器,这四个容器与红黑树结构的关联式容器使用方式基本类似,只是其底层结构不同,本文中只对unordered_map和unordered_set进行介绍,unordered_multimap和unordered_multiset可查看文档介绍。
ordered - 有序的,unordered - 无序的。
1.unordered_map
(1)unordered_map的介绍
unordered_map文档
-
unordered_map是存储<key, value>键值对的关联式容器,其允许通过keys快速的索引到与其对应的value。
-
在unordered_map中,键值通常用于惟一地标识元素,而映射值是一个对象,其内容与此键关联。键和映射值的类型可能不同。
-
在内部,unordered_map没有对<kye, value>按照任何特定的顺序排序, 为了能在常数范围内找到key所对应的value,unordered_map将相同哈希值的键值对放在相同的桶中。
-
unordered_map容器通过key访问单个元素要比map快,但它通常在遍历元素子集的范围迭代方面效率较低。
-
unordered_maps实现了直接访问操作符(operator[]),它允许使用key作为参数直接访问value。
-
它的迭代器至少是前向迭代器。
(2)unordered_map的接口说明
- unordered_map的构造
- unordered_map的容量
- unordered_map的迭代器(只支持单项迭代器)
- unordered_map的元素访问
- unordered_map的查询
- unordered_map的修改操作
- unordered_map的桶操作
略(可自行查看文档)
2. unordered_set
参见文档:unordered_set在线文档说明
3.性能对比
- 代码示例
#include<iostream>
#include<unordered_set>
#include<unordered_map>
#include <map>
#include <set>
#include<string>
using namespace std;#include <time.h>int main()
{const size_t N = 1000000;unordered_set<int> us;set<int> s;vector<int> v;v.reserve(N); //申请空间srand(time(0)); //随机值for (size_t i = 0; i < N; ++i){//v.push_back(rand());//v.push_back(rand()+i);v.push_back(i);}size_t begin1 = clock();for (auto e : v){s.insert(e);}size_t end1 = clock();cout << "set insert:" << end1 - begin1 << endl; size_t begin2 = clock();for (auto e : v){us.insert(e);}size_t end2 = clock();cout << "unordered_set insert:" << end2 - begin2 << endl; size_t begin3 = clock();for (auto e : v){s.find(e);}size_t end3 = clock();cout << "set find:" << end3 - begin3 << endl;size_t begin4 = clock();for (auto e : v){us.find(e);}size_t end4 = clock();cout << "unordered_set find:" << end4 - begin4 << endl; //对比可以发现unordered_set的find更快cout << s.size() << endl;cout << us.size() << endl;size_t begin5 = clock();for (auto e : v){s.erase(e);}size_t end5 = clock();cout << "set erase:" << end5 - begin5 << endl;size_t begin6 = clock();for (auto e : v){us.erase(e);}size_t end6 = clock();cout << "unordered_set erase:" << end6 - begin6 << endl;return 0;
}
- 结果示例

总结:unordered系列容器在 insert、erase上无明显优势,但是在查找(find)方面相较于原来的容器,性能大大提高。
二、底层结构
unordered系列的关联式容器之所以效率比较高,是因为其底层使用了哈希结构。
1.哈希概念
顺序结构以及平衡树中,元素关键码与其存储位置之间没有对应的关系,因此在查找一个元素时,必须要经过关键码的多次比较。顺序查找时间复杂度为O(N),平衡树中为树的高度,即O( l o g 2 N log_2 N log2N),搜索的效率取决于搜索过程中元素的比较次数。
理想的搜索方法:可以不经过任何比较,一次直接从表中得到要搜索的元素。如果构造一种存储结构,通过某种函数(hashFunc)使元素的存储位置与它的关键码之间能够建立一一映射的关系,那么在查找时通过该函数可以很快找到该元素(哈希映射:key值跟储存位置建立关联关系)。
当向该结构中:
- 插入元素
根据待插入元素的关键码,以此函数计算出该元素的存储位置并按此位置进行存放。
- 搜索元素
对元素的关键码进行同样的计算,把求得的函数值当做元素的存储位置,在结构中按此位置取元素比较,若关键码相等,则搜索成功。
该方式即为哈希(散列)方法,哈希方法中使用的转换函数称为哈希(散列)函数,构造出来的结构称为哈希表(Hash Table)(或者称散列表)。
例如:数据集合{1,7,6,4,5,9};
哈希函数设置为:hash(key) = key % capacity; capacity为存储元素底层空间总的大小。
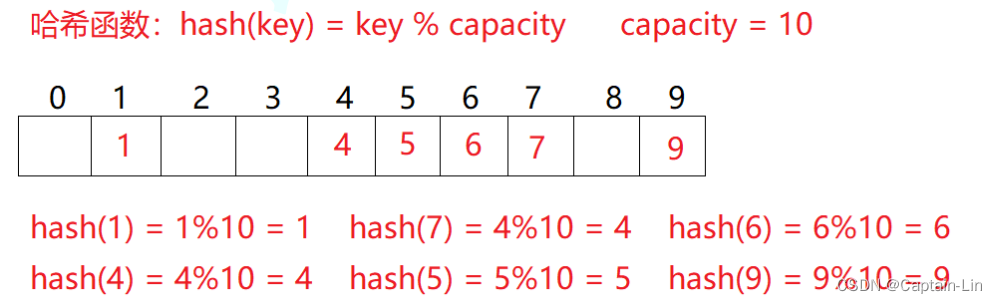
用该方法进行搜索不必进行多次关键码的比较,因此搜索的速度比较快。
问题:按照上述哈希方式,向集合中插入元素44,会出现什么问题?这就涉及到哈希冲突的问题了。
2.哈希冲突
对于两个数据元素的关键字 k i k_i ki和 k j k_j kj(i != j),有 k i k_i ki != k j k_j kj,但有:Hash( k i k_i ki) == Hash( k j k_j kj),即:不同关键字通过相同哈希哈数计算出相同的哈希地址,该种现象称为哈希冲突或哈希碰撞。
把具有不同关键码而具有相同哈希地址的数据元素称为“同义词”。
发生哈希冲突该如何处理呢?
3.哈希函数
引起哈希冲突的一个原因可能是:哈希函数设计不够合理。
哈希函数设计原则:
- 哈希函数的定义域必须包括需要存储的全部关键码,而如果散列表允许有m个地址时,其值域必须在0到m-1之间
- 哈希函数计算出来的地址能均匀分布在整个空间中
- 哈希函数应该比较简单
常见哈希函数
- 直接定址法–(常用)
取关键字的某个线性函数为散列地址:Hash(Key)= A*Key + B
优点:简单、均匀
缺点:需要事先知道关键字的分布情况
使用场景:适合查找比较小且连续的情况 - 除留余数法–(常用)
设散列表中允许的地址数为m,取一个不大于m,但最接近或者等于m的质数p作为除数,
按照哈希函数:Hash(key) = key% p(p<=m),将关键码转换成哈希地址
注意:哈希函数设计的越精妙,产生哈希冲突的可能性就越低,但是无法避免哈希冲突
4.哈希冲突解决
解决哈希冲突两种常见的方法是:闭散列和开散列
(1)闭散列(开放地址法)
闭散列:也叫开放定址法,当发生哈希冲突时,如果哈希表未被装满,说明在哈希表中必然还有空位置,那么可以把key存放到冲突位置中的“下一个” 空位置中去。那如何寻找下一个空位置呢?
1.线性探测
比如2.1中的场景,现在需要插入元素44,先通过哈希函数计算哈希地址,hashAddr为4,因此44理论上应该插在该位置,但是该位置已经放了值为4的元素,即发生哈希冲突。
线性探测:从发生冲突的位置开始,依次向后探测,直到寻找到下一个空位置为止。
- 插入
- 通过哈希函数获取待插入元素在哈希表中的位置
- 如果该位置中没有元素则直接插入新元素,如果该位置中有元素发生哈希冲突,使用线性探测找到下一个空位置,插入新元素

- 删除
- 采用闭散列处理哈希冲突时,不能随便物理删除哈希表中已有的元素,若直接删除元素会影响其他元素的搜索。
- 比如删除元素4,如果直接删除掉,44查找起来可能会受影响。因此线性探测采用标记的伪删除法来删除一个元素。
// 哈希表每个空间给个标记
// EMPTY此位置空, EXIST此位置已经有元素, DELETE元素已经删除
enum State{EMPTY, EXIST, DELETE};
- 线性探测的实现
// 注意:假如实现的哈希表中元素唯一,即key相同的元素不再进行插入
// 为了实现简单,此哈希表中我们将比较直接与元素绑定在一起
template<class K, class V>
class HashTable
{struct Elem{pair<K, V> _val;State _state;};public:HashTable(size_t capacity = 3): _ht(capacity), _size(0){for (size_t i = 0; i < capacity; ++i)_ht[i]._state = EMPTY;}bool Insert(const pair<K, V>& val){// 检测哈希表底层空间是否充足// _CheckCapacity();size_t hashAddr = HashFunc(key);// size_t startAddr = hashAddr;while (_ht[hashAddr]._state != EMPTY){if (_ht[hashAddr]._state == EXIST && _ht[hashAddr]._val.first== key)return false;hashAddr++;if (hashAddr == _ht.capacity())hashAddr = 0;/*// 转一圈也没有找到,注意:动态哈希表,该种情况可以不用考虑,哈希表中元素个数到达一定的数量,哈希冲突概率会增大,需要扩容来降低哈希冲突,因此哈希表中元素是不会存满的if(hashAddr == startAddr)return false;*/}// 插入元素_ht[hashAddr]._state = EXIST;_ht[hashAddr]._val = val;_size++;return true;}int Find(const K& key){size_t hashAddr = HashFunc(key);while (_ht[hashAddr]._state != EMPTY){if (_ht[hashAddr]._state == EXIST && _ht[hashAddr]._val.first== key)return hashAddr;hashAddr++;}return hashAddr;}bool Erase(const K & key){int index = Find(key);if (-1 != index){_ht[index]._state = DELETE;_size++;return true;}return false;}size_t Size()const;bool Empty() const;void Swap(HashTable<K, V, HF>&ht);
private:size_t HashFunc(const K & key){return key % _ht.capacity();}
private:vector<Elem> _ht;size_t _size;
};
- 思考:哈希表什么情况下进行扩容?如何扩容?

void CheckCapacity()
{if (_size * 10 / _ht.capacity() >= 7){HashTable<K, V, HF> newHt(GetNextPrime(ht.capacity));for (size_t i = 0; i < _ht.capacity(); ++i){if (_ht[i]._state == EXIST)newHt.Insert(_ht[i]._val);}Swap(newHt);}
}
负载因子越小,冲突概率越小,消耗空间越多。负载因子越大,冲突概率越大,空间利用率越高。
线性探测优点:实现非常简单。
线性探测缺点:一旦发生哈希冲突,所有的冲突连在一起,容易产生数据“堆积”,即:不同关键码占据了可利用的空位置(插入的数据占据了别的数据关键码对应的空间),使得寻找某关键码的位置需要许多次比较,导致搜索效率降低。如何缓解呢?
2.二次探测
线性探测的缺陷是产生冲突的数据堆积在一块,这与其找下一个空位置有关系,因为找空位置的方式o就是挨着往后逐个去找,因此二次探测为了避免该问题,找下一个空位置的方法为: H i H_i Hi = ( H 0 H_0 H0 + i 2 i^2 i2 )% m, 或者: H i H_i Hi = ( H 0 H_0 H0 - i 2 i^2 i2 )% m。其中:i = 1,2,3…, H 0 H_0 H0是通过散列函数Hash(x)对元素的关键码 key 进行计算得到的位置,m是表的大小。
我们可以将其理解为跳跃式查找空余位置的方法。
研究表明:当表的长度为质数且表装载因子a不超过0.5时,新的表项一定能够插入,而且任何一个位置都不会被探查两次。因此只要表中有一半的空位置,就不会存在表满的问题。在搜索时可以不考虑表装满的情况,但在插入时必须确保表的装载因子a不超过0.5,如果超出必须考虑增容。

因此:比散列最大的缺陷就是空间利用率比较低,这也是哈希的缺陷。
(2)开散列(哈希桶/开链法 - 常用)
1.开散列概念
开散列法又叫链地址法(开链法),首先对关键码集合用散列函数计算散列地址,具有相同地址的关键码归于同一子集合,每一个子集合称为一个桶,各个桶中的元素通过一个单链表链接起来,各链表的头结点存储在哈希表中。

将 44插入到容器中

从上图可以看出,开散列中每个桶中放的都是发生哈希冲突的元素。
2.开散列实现
template<class V>
struct HashBucketNode
{HashBucketNode(const V& data): _pNext(nullptr), _data(data){}HashBucketNode<V>* _pNext;V _data;
};// 本文所实现的哈希桶中key是唯一的
template<class V>
class HashBucket
{typedef HashBucketNode<V> Node;typedef Node* PNode;
public:HashBucket(size_t capacity = 3) : _size(0){_ht.resize(GetNextPrime(capacity), nullptr);}// 哈希桶中的元素不能重复PNode* Insert(const V& data){// 确认是否需要扩容。。。// _CheckCapacity();// 1. 计算元素所在的桶号size_t bucketNo = HashFunc(data);// 2. 检测该元素是否在桶中PNode pCur = _ht[bucketNo];while (pCur){if (pCur->_data == data)return pCur;pCur = pCur->_pNext;}// 3. 插入新元素pCur = new Node(data);pCur->_pNext = _ht[bucketNo];_ht[bucketNo] = pCur;_size++;return pCur;}// 删除哈希桶中为data的元素(data不会重复),返回删除元素的下一个节点PNode* Erase(const V& data){size_t bucketNo = HashFunc(data);PNode pCur = _ht[bucketNo];PNode pPrev = nullptr, pRet = nullptr;while (pCur){if (pCur->_data == data){if (pCur == _ht[bucketNo])_ht[bucketNo] = pCur->_pNext;elsepPrev->_pNext = pCur->_pNext;pRet = pCur->_pNext;delete pCur;_size--;return pRet;}}return nullptr;}PNode* Find(const V& data);size_t Size()const;bool Empty()const;void Clear();bool BucketCount()const;void Swap(HashBucket<V, HF>& ht;~HashBucket();
private:size_t HashFunc(const V& data){return data % _ht.capacity();}
private:vector<PNode*> _ht;size_t _size; // 哈希表中有效元素的个数
};
3.开散列增容
桶的个数是一定的,随着元素的不断插入,每个桶中元素的个数不断增多,极端情况下,可能会导致一个桶中链表节点非常多,会影响的哈希表的性能,因此在一定条件下需要对哈希表进行增容,那该条件怎么确认呢?开散列最好的情况是:每个哈希桶中刚好挂一个节点,再继续插入元素时,每一次都会发生哈希冲突,因此,在元素个数刚好等于桶的个数时,可以给哈希表增容。
void _CheckCapacity()
{size_t bucketCount = BucketCount();if (_size == bucketCount){HashBucket<V, HF> newHt(bucketCount);for (size_t bucketIdx = 0; bucketIdx < bucketCount; ++bucketIdx){PNode pCur = _ht[bucketIdx];while (pCur){// 将该节点从原哈希表中拆出来_ht[bucketIdx] = pCur->_pNext;// 将该节点插入到新哈希表中size_t bucketNo = newHt.HashFunc(pCur->_data);pCur->_pNext = newHt._ht[bucketNo];newHt._ht[bucketNo] = pCur;pCur = _ht[bucketIdx];}}newHt._size = _size;this->Swap(newHt);}
}
4.开散列的思考
- 只能存储key为整形的元素,其他类型怎么解决?
// 哈希函数采用处理余数法,被模的key必须要为整形才可以处理,此处提供将key转化为
整形的方法
// 整形数据不需要转化
template<class T>
class DefHashF
{
public:size_t operator()(const T& val){return val;}
};// key为字符串类型,需要将其转化为整形
class Str2Int
{
public:size_t operator()(const string& s){const char* str = s.c_str();unsigned int seed = 131; // 31 131 1313 13131 131313unsigned int hash = 0;while (*str){hash = hash * seed + (*str++);}return (hash & 0x7FFFFFFF);}
};// 为了实现简单,此哈希表中我们将比较直接与元素绑定在一起
template<class V, class HF>
class HashBucket
{// ……
private:size_t HashFunc(const V& data){return HF()(data.first) % _ht.capacity();}
};
- 除留余数法,最好模一个素数,如何每次快速取一个类似两倍关系的素数?
略(有固定的prime语法)
5.开散列与闭散列比较
应用链地址法处理溢出,需要增设链接指针,似乎增加了存储开销。事实上:由于开地址法必须保持大量的空闲空间以确保搜索效率,如二次探查法要求装载因子a <= 0.7,而表项所占空间又比指针大的多,所以使用链地址法反而比开地址法节省存储空间。
三、模拟实现
略
四、哈希的应用
1.位图
(1)位图概念
1.面试题
给40亿个不重复的无符号整数,没排过序。给一个无符号整数,如何快速判断一个数是否在
这40亿个数中。【腾讯】
-
遍历,时间复杂度O(N)
-
排序(O(NlogN)),利用二分查找: logN
-
位图解决
-
数据是否在给定的整形数据中,结果是在或者不在,刚好是两种状态,那么可以使用一个二进制比特位来代表数据是否存在的信息,如果二进制比特位为1,代表存在,为0代表不存在。比如:
-
图一:
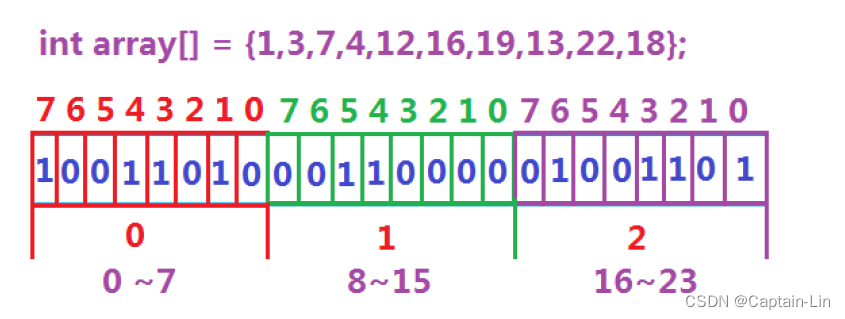
-
2.位图概念
所谓位图,就是用每一位来存放某种状态,适用于海量数据,数据无重复的场景。通常是用来判断某个数据存不存在的。
(2)位图的实现
namespace Bitmap
{template<size_t N>class Bitmapset{public:bitset(){//_bits.resize(N/8+1, 0);_bits.resize((N >> 3) + 1, 0);}// 将x比特位置1void set(size_t x){//size_t i = x / 8;size_t i = x >> 3;size_t j = x % 8;_bits[i] |= (1 << j);}// 将x比特位置0void reset(size_t x){size_t i = x >> 3;size_t j = x % 8;_bits[i] &= (~(1 << j));}// 检测位图中x是否为1bool test(size_t x){size_t i = x >> 3;size_t j = x % 8;return _bits[i] & (1 << j);}private:vector<char> _bits;};void test_bitset(){//bitset<100> bs1;//bitset<-1> bs2;bitset<0xffffffff> bs2;bs2.set(10);bs2.set(10000);bs2.set(8888);cout << bs2.test(10) << endl;cout << bs2.test(10000) << endl;cout << bs2.test(8888) << endl;cout << bs2.test(8887) << endl;cout << bs2.test(9999) << endl << endl;bs2.reset(8888);bs2.set(8887);cout << bs2.test(10) << endl;cout << bs2.test(10000) << endl;cout << bs2.test(8888) << endl;cout << bs2.test(8887) << endl;cout << bs2.test(9999) << endl;}}
(3)位图的应用
- 快速查找某个数据是否在一个集合中
- 排序 + 去重
- 求两个集合的交集、并集等
- 操作系统中磁盘块标记
2.布隆过滤器
(1)布隆过滤器的提出
我们在使用新闻客户端看新闻时,它会给我们不停地推荐新的内容,它每次推荐时要去重,去掉那些已经看过的内容。问题来了,新闻客户端推荐系统如何实现推送去重的? 用服务器记录了用户看过的所有历史记录,当推荐系统推荐新闻时会从每个用户的历史记录里进行筛选,过滤掉那些已经存在的记录。 如何快速查找呢?
-
用哈希表存储用户记录,缺点:浪费空间
-
用位图存储用户记录,缺点:位图一般只能处理整形,如果内容编号是字符串,就无法处理了。
-
将哈希与位图结合,即布隆过滤器
(2)布隆过滤器概念
布隆过滤器是由布隆(Burton Howard Bloom)在1970年提出的 一种紧凑型的、比较巧妙的概率型数据结构,特点是高效地插入和查询,可以用来告诉你 “某样东西一定不存在或者可能存在”,它是用多个哈希函数,将一个数据映射到位图结构中。此种方式不仅可以提升查询效率,也可以节省大量的内存空间。

(3)布隆函数的插入

- 向布隆过滤器中插入:“baidu”,将一个元素用多个哈希函数转成一个整形映射到一个位图中,被映射到的位置的比特位由0修改为1


struct BKDRHash
{size_t operator()(const string& s){// BKDRsize_t value = 0;for (auto ch : s){value *= 31;value += ch;}return value;}
};struct APHash
{size_t operator()(const string& s){size_t hash = 0;for (long i = 0; i < s.size(); i++){if ((i & 1) == 0){hash ^= ((hash << 7) ^ s[i] ^ (hash >> 3));}else{hash ^= (~((hash << 11) ^ s[i] ^ (hash >> 5)));}}return hash;}
};struct DJBHash
{size_t operator()(const string& s){size_t hash = 5381;for (auto ch : s){hash += (hash << 5) + ch;}return hash;}
};template<size_t N,size_t X = 5,class K = string,class HashFunc1 = BKDRHash,class HashFunc2 = APHash,class HashFunc3 = DJBHash>class BloomFilter
{
public:void Set(const K& key){size_t len = X * N;size_t index1 = HashFunc1()(key) % len;size_t index2 = HashFunc2()(key) % len;size_t index3 = HashFunc3()(key) % len;/* cout << index1 << endl;cout << index2 << endl;cout << index3 << endl<<endl;*/_bs.set(index1);_bs.set(index2);_bs.set(index3);}bool Test(const K& key){size_t len = X * N;size_t index1 = HashFunc1()(key) % len;if (_bs.test(index1) == false)return false;size_t index2 = HashFunc2()(key) % len;if (_bs.test(index2) == false)return false;size_t index3 = HashFunc3()(key) % len;if (_bs.test(index3) == false)return false;return true; // 存在误判的}// 不支持删除,删除可能会影响其他值。void Reset(const K& key);private:bitset<X* N> _bs;
};
(4)布隆过滤器的查找(重点)
布隆过滤器的思想是将一个元素用多个哈希函数映射到一个位图中,因此被映射到的位置的比特位一定为1**。所以可以按照以下方式进行查找:分别计算每个哈希值对应的比特位置存储的是否为零,只要有一个为零,代表该元素一定不在哈希表中,否则可能在哈希表中。
注意:布隆过滤器如果说某个元素不存在时,该元素一定不存在,如果该元素存在时,该元素可能存在,因为有些哈希函数存在一定的误判。
比如:在布隆过滤器中查找"alibaba"时,假设3个哈希函数计算的哈希值为:1、3、7,刚好和其他元素的比特位重叠,此时布隆过滤器告诉该元素存在,但实该元素是不存在的。
(5)布隆过滤器的删除
布隆过滤器不能直接支持删除工作,因为在删除一个元素时,可能会影响其他元素。
比如:删除上图中"tencent"元素,如果直接将该元素所对应的二进制比特位置0,“baidu”元素也被删除了,因为这两个元素在多个哈希函数计算出的比特位上刚好有重叠。
一种支持删除的方法:将布隆过滤器中的每个比特位扩展成一个小的计数器,插入元素时给k个计数器(k个哈希函数计算出的哈希地址)加一,删除元素时,给k个计数器减一,通过多占用几倍存储空间的代价来增加删除操作。
缺陷:
- 无法确认元素是否真正在布隆过滤器中
- 存在计数回绕
(6)布隆过滤器的优点
-
增加和查询元素的时间复杂度为:O(K), (K为哈希函数的个数,一般比较小),与数据量大小无关
-
哈希函数相互之间没有关系,方便硬件并行运算
-
布隆过滤器不需要存储元素本身,在某些对保密要求比较严格的场合有很大优势
-
在能够承受一定的误判时,布隆过滤器比其他数据结构有这很大的空间优势
-
数据量很大时,布隆过滤器可以表示全集,其他数据结构不能
-
使用同一组散列函数的布隆过滤器可以进行交、并、差运算
(7)布隆过滤器的缺陷
-
有误判率,即存在假阳性(False Position),即不能准确判断元素是否在集合中(补救方法:再建立一个白名单,存储可能会误判的数据)
-
不能获取元素本身
-
一般情况下不能从布隆过滤器中删除元素
-
如果采用计数方式删除,可能会存在计数回绕问题
五、海量数据面试题
1.哈希切割
(1)给一个超过100G大小的log file, log中存着IP地址, 设计算法找到出现次数最多的IP地址?
思路:将大文件通过哈希切割成小文件,此时同一个ip只会在同一个小文件中。找出1号小文件中出现次数最多的ip,将它拿出来和2、3…号出现最多的ip进行比较,最后将出现次数最多的ip返回
(2)与上题条件相同,如何找到top K的IP?如何直接用Linux系统命令实现?
思路:在上题的基础上再引入一个堆即可
2.位图应用
(1)给定100亿个整数,设计算法找到只出现一次的整数?
思路:可以开多个位图进行对应组合,我们可以用00,01,10来表示某个数没有出现、出现一次、出现一次以上,此时只需要创建三个位图并将它们对应起来即可。
(2)给两个文件,分别有100亿个整数,我们只有1G内存,如何找到两个文件交集?
思路:
(3)位图应用变形:1个文件有100亿个int,1G内存,设计算法找到出现次数不超过2次的所有整数
思路:设计一个位图,给对应的数据增加状态标识
3.布隆过滤器
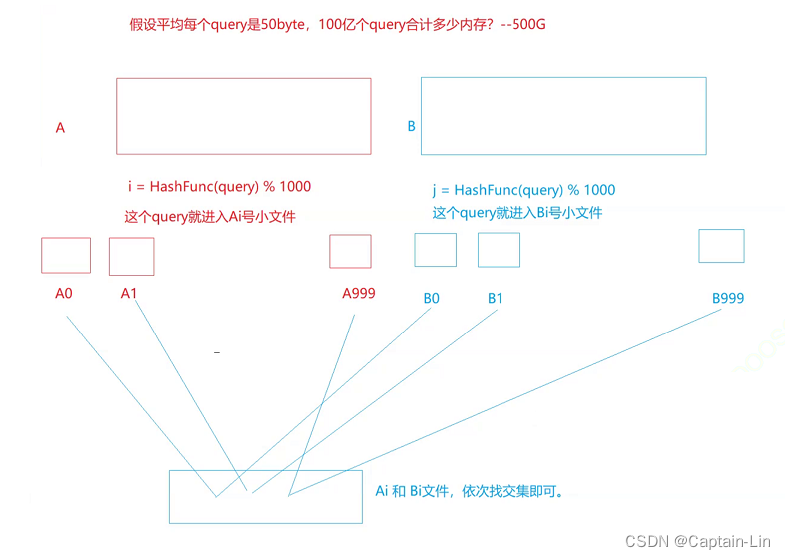
(1)给两个文件,分别有100亿个query,我们只有1G内存,如何找到两个文件交集?分别给出精确算法和近似算法
思路:把其中一个文件放到布隆过滤器中,再用另一个文件去里面找一下,交集一定会在里面,也可能误判(近似算法)。对两个文件进行切割处理,再对比。
(2)如何扩展BloomFilter使得它支持删除元素的操作
一种支持删除的方法:将布隆过滤器中的每个比特位扩展成一个小的计数器,插入元素时给k个计数器(k个哈希函数计算出的哈希地址)加一,删除元素时,给k个计数器减一,通过多占用几倍存储空间的代价来增加删除操作。
🌹🌹 哈希 的知识大概就讲到这里啦,博主后续会继续更新更多C++ 和 Linux的相关知识,干货满满,如果觉得博主写的还不错的话,希望各位小伙伴不要吝啬手中的三连哦!你们的支持是博主坚持创作的动力!💪💪
相关文章:
【C++进阶之路】第五篇:哈希
文章目录 一、unordered系列关联式容器1.unordered_map(1)unordered_map的介绍(2)unordered_map的接口说明 2. unordered_set3.性能对比 二、底层结构1.哈希概念2.哈希冲突3.哈希函数4.哈希冲突解决(1)闭散…...

CentOS基Docker容器时区配置解决方案
配置Docker容器的时区对于确保应用程序正确处理日期和时间至关重要。当使用CentOS作为基础镜像时,可以通过以下两种方法配置时区: 方法一:在Dockerfile中设置时区 这种方法涉及在构建Docker镜像的过程中设置时区。 步骤 选择基础镜像&…...
探索 Material 3:全新设计系统和组件库的介绍
探索 Material 3:全新设计系统和组件库的介绍 一、Material 3 简介1.1 Material 3 的改进和更新1.2 Material 3 的优势特点 二、Material 3 主题使用2.1 使用 Material3 主题2.2 使用 Material3 主题颜色 三、Material 3 组件使用3.1 MaterialButton:支持…...
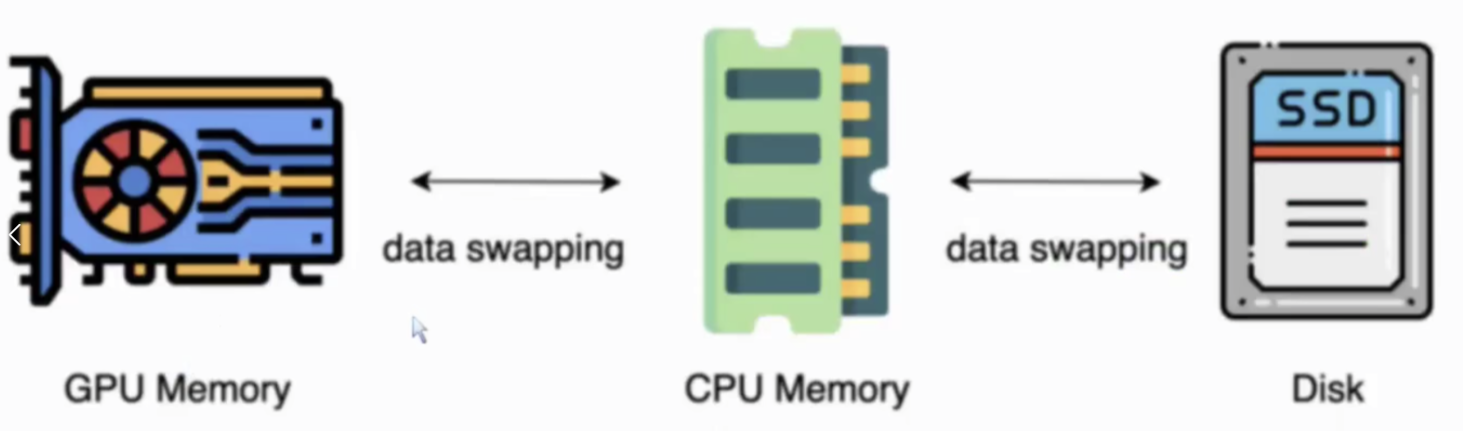
《多GPU大模型训练与微调手册》
全参数微调 Lora微调 PTuning微调 多GPU微调预备知识 1. 参数数据类型 torch.dtype 1.1 半精度 half-precision torch.float16:fp16 就是 float16,1个 sign(符号位),5个 exponent bits(指数位),10个 ma…...
)
【C++】const与类(const修饰函数的三种位置)
目录 const基本介绍 正文 前: 中: 后: 拷贝构造使用const 目录 const基本介绍 正文 前: 中: 后: 拷贝构造使用const const基本介绍 const 是 C 中的修饰符,用于声明常量或表示不可修改的对象、函数或成员函数。 我们已经了解了const基本用法,我们先进行…...

深度学习在图像识别中的革命性应用
深度学习在图像识别中的革命性应用标志着计算机视觉领域的重大进步。以下是深度学习在图像识别方面的一些革命性应用: 1. **卷积神经网络(CNN)的崭新时代**: - CNN是深度学习在图像识别中的核心技术,通过卷积层、池化…...

R语言读文件“-“变成“.“
R语言读取文件时发生"-"变成"." 如果使用read.table函数,需要 check.namesFALSE data <- read.table("data.tsv", headerTRUE, row.names1, check.namesFALSE)怎样将"."还原为"-" 方法一:gsub函…...
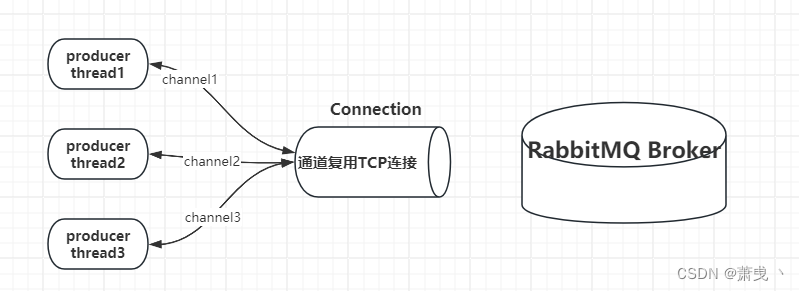
RabbitMQ 基础操作
概念 从计算机术语层面来说,RabbitMQ 模型更像是一种交换机模型。 Queue 队列 Queue:队列,是RabbitMQ 的内部对象,用于存储消息。 RabbitMQ 中消息只能存储在队列中,这一点和Kafka相反。Kafka将消息存储在topic&am…...

自然语言处理:Transformer与GPT
Transformer和GPT(Generative Pre-trained Transformer)是深度学习和自然语言处理(NLP)领域的两个重要概念,它们之间存在密切的关系但也有明显的不同。 1 基本概念 1.1 Transformer基本概念 Transformer是一种深度学…...

Ps:裁剪工具 - 裁剪预设的应用
裁剪工具提供了两种类型的裁剪方式。 一种是仅按宽高比(比例)进行裁剪,常在对图像进行二次构图时采用。 另一种则按指定的图像尺寸(宽度值和高度值)及分辨率(宽 x 高 x 分辨率)进行裁剪。其实质…...

前端工程化-什么是构建工具
了解构建工具之前,我们首先要知道的是浏览器只认识html、css、js,而我们开发时用的vue,react框架都只是为了方便我们开发而使用的工具 使用构建工具的原因 vue或react的企业级项目里都会具备这些功能: 1.使用typescript语言&…...
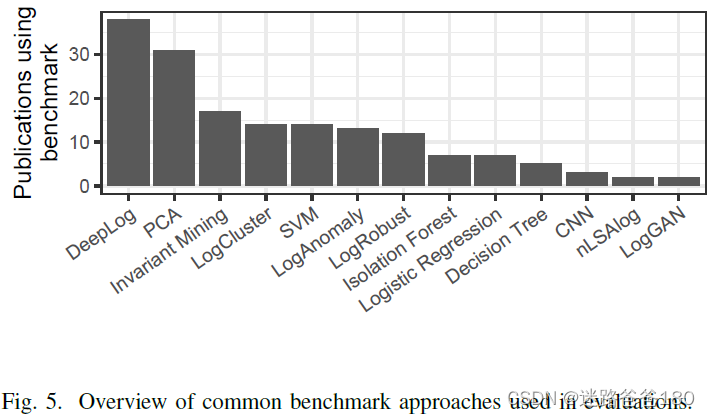
01-论文阅读-Deep learning for anomaly detection in log data: a survey
01-论文阅读-Deep learning for anomaly detection in log data: a survey 文章目录 01-论文阅读-Deep learning for anomaly detection in log data: a survey摘要I 介绍II 背景A 初步定义B 挑战 III 调查方法A 搜索策略B 审查的功能 IV 调查结果A 文献计量学B 深度学习技术C …...

图像处理02 matlab中NSCT的使用
06 matlab中NSCT的使用 最近在学习NSCT相关内容,奈何网上资源太少,简单看了些论文找了一些帖子才懂了一点点,在此分享给大家,希望有所帮助。 一.NSCT流程 首先我们先梳理一下NSCT变换的流程,只有清楚流程才更好的理清…...
提升办公效率,畅享多功能办公笔记软件Notion for Mac
在现代办公环境中,高效的笔记软件对于提高工作效率至关重要。而Notion for Mac作为一款全能的办公笔记软件,将成为你事业成功的得力助手。 Notion for Mac以其多功能和灵活性而脱颖而出。无论你是需要记录会议笔记、管理项目任务、制定流程指南…...
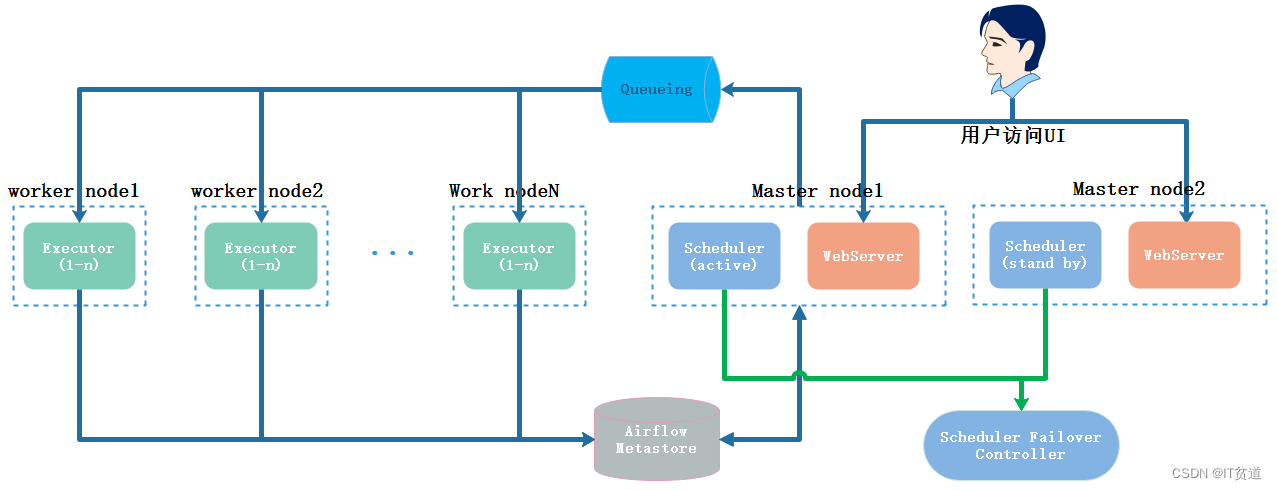
Apache Airflow (十三) :Airflow分布式集群搭建及使用-原因及
🏡 个人主页:IT贫道_大数据OLAP体系技术栈,Apache Doris,Clickhouse 技术-CSDN博客 🚩 私聊博主:加入大数据技术讨论群聊,获取更多大数据资料。 🔔 博主个人B栈地址:豹哥教你大数据的个人空间-豹…...

# 聚类系列(一)——什么是聚类?
目前在做聚类方面的科研工作, 看了很多相关的论文, 也做了一些工作, 于是想出个聚类系列记录一下, 主要包括聚类的概念和相关定义、现有常用聚类算法、聚类相似性度量指标、聚类评价指标、 聚类的应用场景以及共享一些聚类的开源代码 下面正式进入该系列的第一个部分ÿ…...
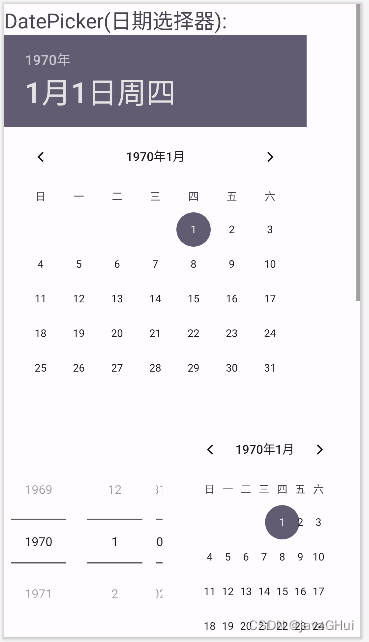
Android DatePicker(日期选择器)、TimePicker(时间选择器)、CalendarView(日历视图)- 简单应用
示意图: layout布局文件:xml <?xml version"1.0" encoding"utf-8"?> <ScrollView xmlns:android"http://schemas.android.com/apk/res/android"xmlns:app"http://schemas.android.com/apk/res-auto"…...

linux环境搭建mysql5.7总结
以下安装方式,在阿里云与腾讯云服务器上都测试可用。 一、进入到opt目录下,执行: [rootmaster opt]# wget https://dev.mysql.com/get/Downloads/MySQL-5.7/mysql-5.7.26-linux-glibc2.12-x86_64.tar.gz解压: [rootmaster opt]#…...
函数)
SQL Server Count()函数
SQL Server Count()函数 SQL Server COUNT() 是一个聚合函数,它返回在集合中找到的项目数。 COUNT() 函数语法: COUNT([ALL | DISTINCT ] expression)ALL 指示COUNT() 函数应用于所有值。ALL是默认值。返回非NULL值的数量(包括重复值&…...
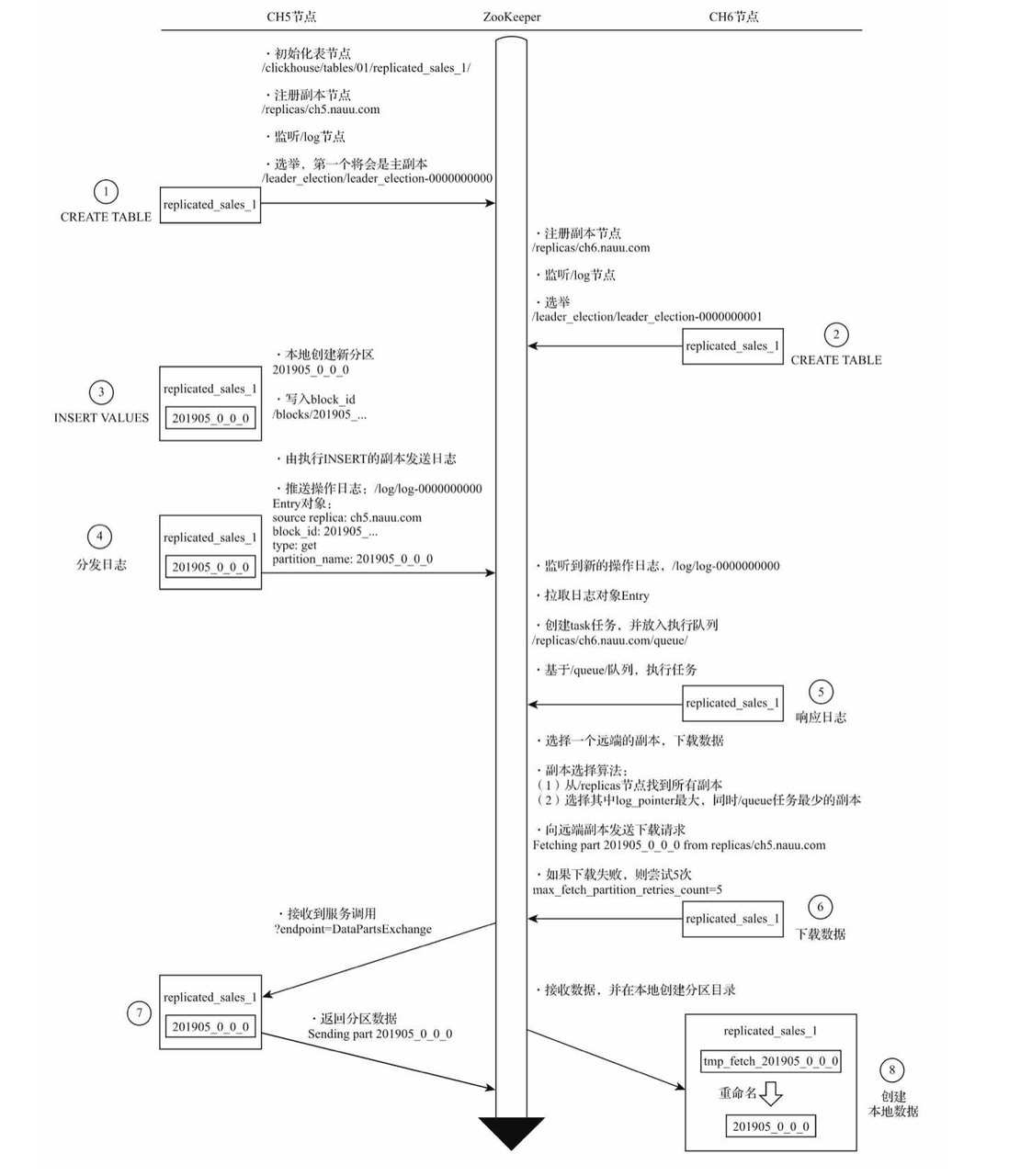
架构探索之路-第一站-clickhouse | 京东云技术团队
一、前言 架构, 软件开发中最熟悉不过的名词, 遍布在我们的日常开发工作中, 大到项目整体, 小到功能组件, 想要实现高性能、高扩展、高可用的目标都需要优秀架构理念辅助. 所以本人尝试编写架构系列文章, 去剖析市面上那些经典优秀的开源项目, 学习优秀的架构理念来积累架构设…...

变量 varablie 声明- Rust 变量 let mut 声明与 C/C++ 变量声明对比分析
一、变量声明设计:let 与 mut 的哲学解析 Rust 采用 let 声明变量并通过 mut 显式标记可变性,这种设计体现了语言的核心哲学。以下是深度解析: 1.1 设计理念剖析 安全优先原则:默认不可变强制开发者明确声明意图 let x 5; …...

C++_核心编程_多态案例二-制作饮品
#include <iostream> #include <string> using namespace std;/*制作饮品的大致流程为:煮水 - 冲泡 - 倒入杯中 - 加入辅料 利用多态技术实现本案例,提供抽象制作饮品基类,提供子类制作咖啡和茶叶*//*基类*/ class AbstractDr…...
)
云计算——弹性云计算器(ECS)
弹性云服务器:ECS 概述 云计算重构了ICT系统,云计算平台厂商推出使得厂家能够主要关注应用管理而非平台管理的云平台,包含如下主要概念。 ECS(Elastic Cloud Server):即弹性云服务器,是云计算…...

在鸿蒙HarmonyOS 5中实现抖音风格的点赞功能
下面我将详细介绍如何使用HarmonyOS SDK在HarmonyOS 5中实现类似抖音的点赞功能,包括动画效果、数据同步和交互优化。 1. 基础点赞功能实现 1.1 创建数据模型 // VideoModel.ets export class VideoModel {id: string "";title: string ""…...

AtCoder 第409场初级竞赛 A~E题解
A Conflict 【题目链接】 原题链接:A - Conflict 【考点】 枚举 【题目大意】 找到是否有两人都想要的物品。 【解析】 遍历两端字符串,只有在同时为 o 时输出 Yes 并结束程序,否则输出 No。 【难度】 GESP三级 【代码参考】 #i…...

【Go】3、Go语言进阶与依赖管理
前言 本系列文章参考自稀土掘金上的 【字节内部课】公开课,做自我学习总结整理。 Go语言并发编程 Go语言原生支持并发编程,它的核心机制是 Goroutine 协程、Channel 通道,并基于CSP(Communicating Sequential Processes࿰…...
)
是否存在路径(FIFOBB算法)
题目描述 一个具有 n 个顶点e条边的无向图,该图顶点的编号依次为0到n-1且不存在顶点与自身相连的边。请使用FIFOBB算法编写程序,确定是否存在从顶点 source到顶点 destination的路径。 输入 第一行两个整数,分别表示n 和 e 的值(1…...

关于easyexcel动态下拉选问题处理
前些日子突然碰到一个问题,说是客户的导入文件模版想支持部分导入内容的下拉选,于是我就找了easyexcel官网寻找解决方案,并没有找到合适的方案,没办法只能自己动手并分享出来,针对Java生成Excel下拉菜单时因选项过多导…...

Vue 模板语句的数据来源
🧩 Vue 模板语句的数据来源:全方位解析 Vue 模板(<template> 部分)中的表达式、指令绑定(如 v-bind, v-on)和插值({{ }})都在一个特定的作用域内求值。这个作用域由当前 组件…...

Elastic 获得 AWS 教育 ISV 合作伙伴资质,进一步增强教育解决方案产品组合
作者:来自 Elastic Udayasimha Theepireddy (Uday), Brian Bergholm, Marianna Jonsdottir 通过搜索 AI 和云创新推动教育领域的数字化转型。 我们非常高兴地宣布,Elastic 已获得 AWS 教育 ISV 合作伙伴资质。这一重要认证表明,Elastic 作为 …...




