-bash: ./deploy.sh: /bin/bash^M: bad interpreter: No such file or directory
文章目录
- 场景
- 解决
场景
jenkins 发布失败, 报错ERROR: Exception when publishing, exception message [Exec exit status not zero. Status [126]], 这说明远程服务器的deploy.sh执行失败, 首先检查权限,没有发现问题,然后手动执行一遍又报错"-bash: ./deploy.sh: /bin/bash^M: bad interpreter: No such file or directory", 这个意味着脚本是windows回车符结尾
[JENKINS] Archiving /home/vagrant/.jenkins/workspace/jenkinsDemo/target/jenkinsDemo-1.0-SNAPSHOT.jar to com.carsonlius/jenkinsDemo/1.0-SNAPSHOT/jenkinsDemo-1.0-SNAPSHOT.jar
channel stopped
SSH: Connecting from host [ubuntu-xenial]
SSH: Connecting with configuration [107.173.111.224 自己] ...
SSH: EXEC: completed after 604 ms
SSH: Disconnecting configuration [107.173.111.224 自己] ...
ERROR: Exception when publishing, exception message [Exec exit status not zero. Status [126]]
Build step 'Send build artifacts over SSH' changed build result to UNSTABLE
解决
sed -i -e ‘s/\r$//’ deploy.sh
相关文章:

-bash: ./deploy.sh: /bin/bash^M: bad interpreter: No such file or directory
文章目录 场景解决 场景 jenkins 发布失败, 报错ERROR: Exception when publishing, exception message [Exec exit status not zero. Status [126]], 这说明远程服务器的deploy.sh执行失败, 首先检查权限,没有发现问题,然后手动执行一遍又报错"-ba…...

【文末送书】十大排序算法C++代码实现
欢迎关注博主 Mindtechnist 或加入【智能科技社区】一起学习和分享Linux、C、C、Python、Matlab,机器人运动控制、多机器人协作,智能优化算法,滤波估计、多传感器信息融合,机器学习,人工智能等相关领域的知识和技术。关…...
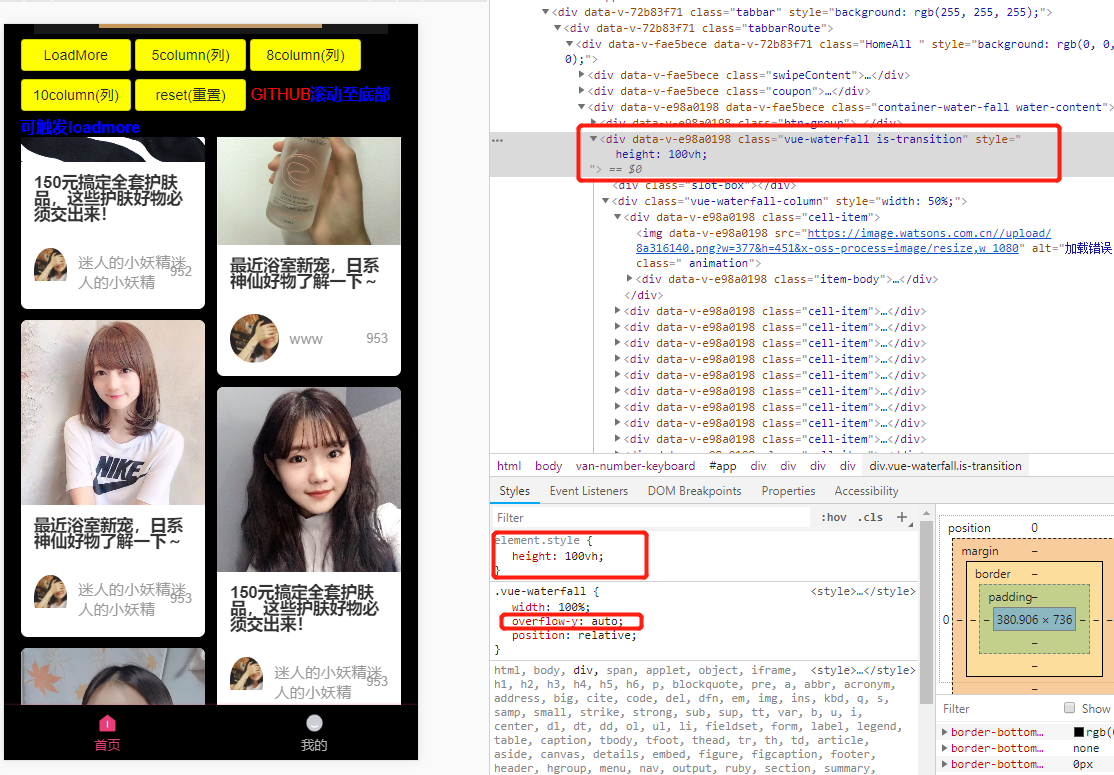
vue-waterfall2 实现瀑布流,及总结的问题
注意:引入需要在主界面引入,直接在组件中引用会有问题 1.安装 npm install vue-waterfall21.8.20 --save (提示:一定要安装1.8.20,最新版会有一部分问题) 2.打开main.js文件 import waterfall from v…...

grafana二次启动失败
背景 安装grafana后启动使用正常,但是关机后再启动显示启动失败,但是看日志又没有报错信息,但是就是启动不了 原因分析 其实是/var/lib/grafana/grafana.db文件损坏了,所以需要把这个文件删掉之后重新启动就正常了,…...

C/C++杂谈-printf的可变参数机制
C/C杂谈-printf的可变参数机制 文章目录 C/C杂谈-printf的可变参数机制printf的使用printf的源码源码剖析 多参数实现机制原理 C11引入了可变参数模板机制,对模板参数进行了高度泛化,但是对于可变参数其实C语言学习中早已遇到过,那就是printf…...
)
es基本语法 (kibana)
#添加 (不添加id默认会生成id) POST /cj/test {"name":"jack","sex":"1","age":12 } #添加 (id为第5个的) POST /cj/test/5 {"name":"jackson","sex":"1","age":12 } #条…...

Tesco EDI需求分析
Tesco,成立于1919年,是一家全球领先的综合性零售企业,总部位于英国。公司致力于提供高质量、多样化的商品和服务,以满足客户的需求。Tesco的使命是通过创新和卓越的客户服务,为客户创造更美好的生活。多年来࿰…...

html常用的标签
基本结构标签 <!DOCTYPE>: 定义 HTML 文档类型。<html>: HTML 文档的根元素。<head>: 文档的头部,包含了元数据和引用的外部资源。<title>: 定义网页标题,显示在浏览器标签上。&l…...

护眼灯什么价位的好?适合学生入手的护眼台灯推荐
据60年前的统计,中国人口的近视率约为10%至20%。 国家卫健委发布的中国首份眼健康白皮书显示,我国小学生近视率为47.2%,初中生近视率为75.8%,大学生近视率超过90%。如今,“低头族”随处可见,近视人群日益增…...

大数据架构
大数据架构 https://huaweicloud.csdn.net/633578fed3efff3090b58398.html https://blog.csdn.net/yuanziok/article/details/117030031 https://blog.csdn.net/qq_46675545/article/details/121985987 https://blog.csdn.net/qq_33367934/article/details/127685417 https://b…...
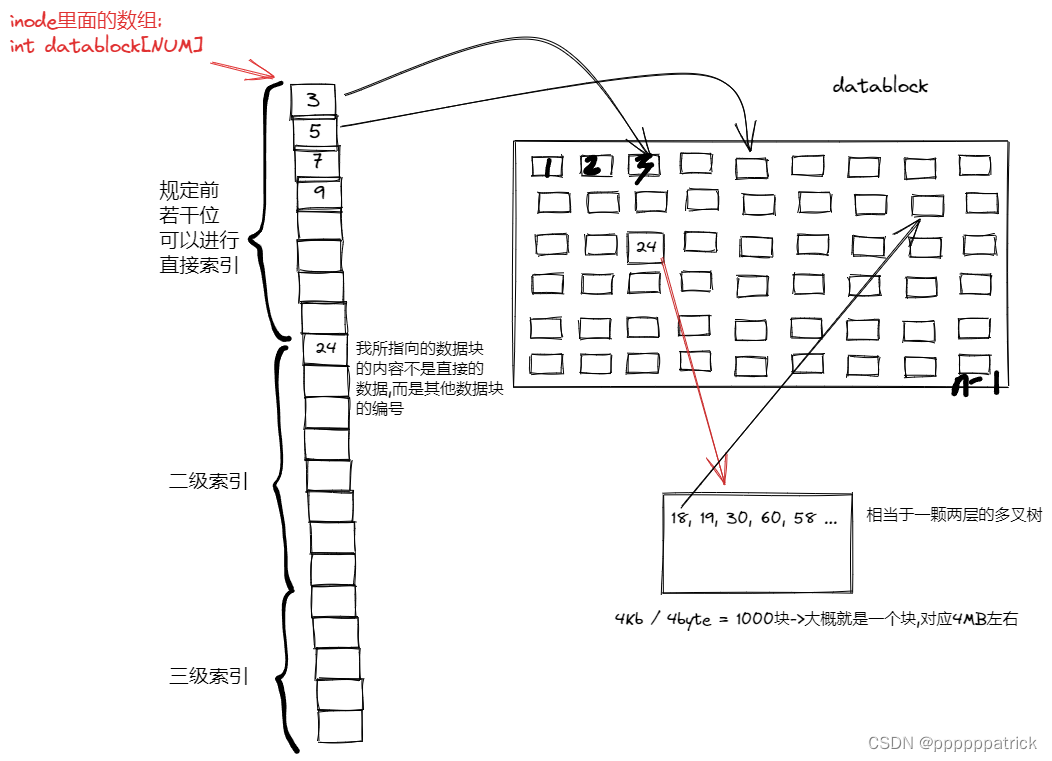
【Linux】C文件系统详解(四)——磁盘的物理和抽象结构
文章目录 磁盘结构磁盘物理结构磁盘的具体物理结构磁盘结构的逻辑抽象 文件系统BootBlockSuperBlockGroupDescriptorTableinode tableDataBlocksinodeBitmapblockBitmaplinux中的inode 和文件名如何理解文件的增删查改删 补充细节1.如果文件误删了,我们该怎么办?2.inode确定分…...
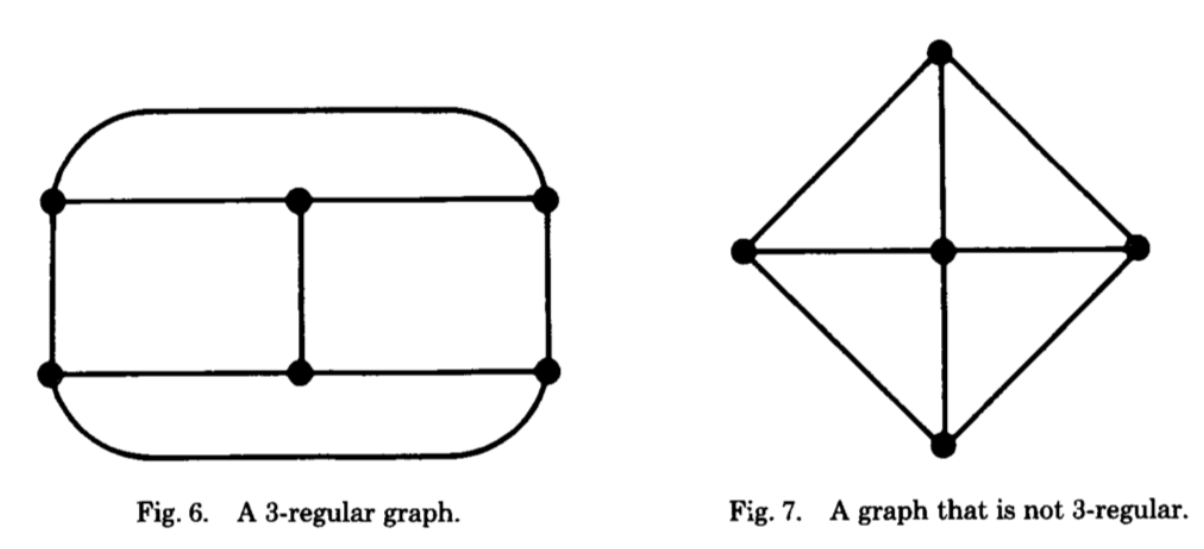
论文-分布式-拜占庭将军问题
目录 0-前言 1-导引 2-不可能性 3将军(1叛徒)问题不存在解/不能达成共识 少于3m1个将军(有m个叛徒)不存在解/不能达成共识 精确一致性与近似一致性是同等困难的 3-使用口头消息的解 “口头消息”的含义 OM(m)算法的步骤 OM(m)算法的正确性推导 4-使用签名消息情况下…...
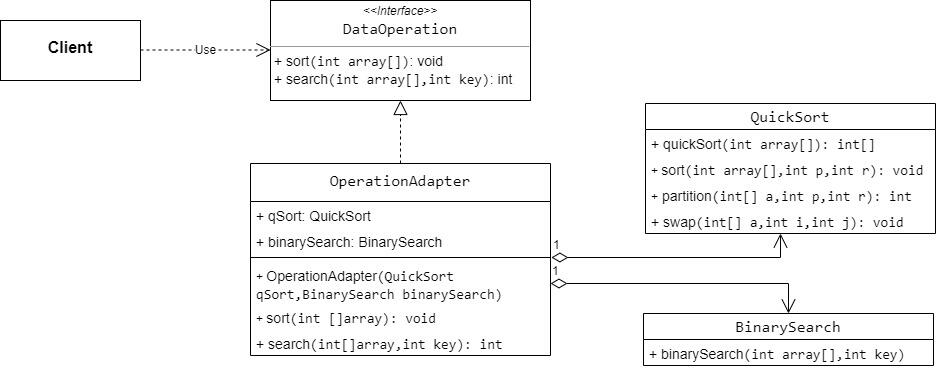
万字解析设计模式之 适配器模式
一、 适配器模式 1.1概述 将一个接口转换成客户希望的另一个接口,适配器模式使接口不兼容的那些类可以一起工作。 适配器模式分为类适配器模式和对象适配器模式,前者类之间的耦合度比后者高,且要求程序员了解现有组件库中的相关组件的内部结…...

Linux 安全 - 扩展属性xattr
文章目录 前言一、简介二、扩展属性命名空间2.1 简介2.2 security扩展属性2.3 System扩展属性2.4 Trusted扩展属性2.5 User扩展属性 三、用户空间使用3.1 setfattr/getfattr3.2 setxattr/getxattr/listxattr 参考资料 前言 一、简介 xattr - Extended attributes扩展属性是与…...

spring boot加mybatis puls实现,在新增/修改时,对某些字段进行处理,使用的@TableField()或者AOP @Before
1.先说场景,在对mysql数据库表数据插入或者更新时都得记录时间和用户id 传统实现有点繁琐,这里还可以封装一下公共方法。 2.解决方法: 2.1:使用aop切面编程(记录一下,有时间再攻克)。 2.1.1&am…...
我的创作纪念日2048天
机缘 在这特殊的日子里,我要庆祝我的 CSDN 创作纪念日——已经坚持了整整2048天! 在这2048天里,我经历了很多成长和收获。作为一名技术写手,我投入了大量的时间和精力来分享我的知识和经验。我曾经写过关于数据库、数据同步、数…...

MatrixOne实战系列回顾 | 导入导出项目场景实践
本次分享主要介绍MatrixOne导入导出以及项目场景实践。将从四个方向为大家演示MatrixOne的功能,分别是数据的导入、导出、对接数据集成工具,以及Java连接实战。 数据导入会使用三种方式将数据导入至 MatrixOne中。分别是insert语句、load data语句还有s…...

Find My音箱|苹果Find My技术与音箱结合,智能防丢,全球定位
音箱市场规模正在不断扩大。随着人们生活品质的提高,对音乐体验的需求也在不断升级。消费者对于蓝牙音箱的需求,已经从单纯的音质扩展到了功能、设计和价格等多个方面。随着移动化、即时化的视听娱乐需求的增长,蓝牙音箱性能、质量、外观设计…...

51单片机应用
目录 编辑 1. C51的数据类型 1.1 C51中的基本数据类型 1.2 特殊功能寄存器类型 2. C51的变量 2.1 存储种类 1. C51的数据类型 C51是一种基于8051架构的单片机,它支持以下基本数据类型: 位(Bit):可以表…...

业务系统对接大模型的基础方案:架构设计与关键步骤
业务系统对接大模型:架构设计与关键步骤 在当今数字化转型的浪潮中,大语言模型(LLM)已成为企业提升业务效率和创新能力的关键技术之一。将大模型集成到业务系统中,不仅可以优化用户体验,还能为业务决策提供…...

C++:std::is_convertible
C++标志库中提供is_convertible,可以测试一种类型是否可以转换为另一只类型: template <class From, class To> struct is_convertible; 使用举例: #include <iostream> #include <string>using namespace std;struct A { }; struct B : A { };int main…...

【AI学习】三、AI算法中的向量
在人工智能(AI)算法中,向量(Vector)是一种将现实世界中的数据(如图像、文本、音频等)转化为计算机可处理的数值型特征表示的工具。它是连接人类认知(如语义、视觉特征)与…...

JDK 17 新特性
#JDK 17 新特性 /**************** 文本块 *****************/ python/scala中早就支持,不稀奇 String json “”" { “name”: “Java”, “version”: 17 } “”"; /**************** Switch 语句 -> 表达式 *****************/ 挺好的ÿ…...

代码随想录刷题day30
1、零钱兑换II 给你一个整数数组 coins 表示不同面额的硬币,另给一个整数 amount 表示总金额。 请你计算并返回可以凑成总金额的硬币组合数。如果任何硬币组合都无法凑出总金额,返回 0 。 假设每一种面额的硬币有无限个。 题目数据保证结果符合 32 位带…...

Python Ovito统计金刚石结构数量
大家好,我是小马老师。 本文介绍python ovito方法统计金刚石结构的方法。 Ovito Identify diamond structure命令可以识别和统计金刚石结构,但是无法直接输出结构的变化情况。 本文使用python调用ovito包的方法,可以持续统计各步的金刚石结构,具体代码如下: from ovito…...

[论文阅读]TrustRAG: Enhancing Robustness and Trustworthiness in RAG
TrustRAG: Enhancing Robustness and Trustworthiness in RAG [2501.00879] TrustRAG: Enhancing Robustness and Trustworthiness in Retrieval-Augmented Generation 代码:HuichiZhou/TrustRAG: Code for "TrustRAG: Enhancing Robustness and Trustworthin…...

GraphQL 实战篇:Apollo Client 配置与缓存
GraphQL 实战篇:Apollo Client 配置与缓存 上一篇:GraphQL 入门篇:基础查询语法 依旧和上一篇的笔记一样,主实操,没啥过多的细节讲解,代码具体在: https://github.com/GoldenaArcher/graphql…...

AD学习(3)
1 PCB封装元素组成及简单的PCB封装创建 封装的组成部分: (1)PCB焊盘:表层的铜 ,top层的铜 (2)管脚序号:用来关联原理图中的管脚的序号,原理图的序号需要和PCB封装一一…...

多元隐函数 偏导公式
我们来推导隐函数 z z ( x , y ) z z(x, y) zz(x,y) 的偏导公式,给定一个隐函数关系: F ( x , y , z ( x , y ) ) 0 F(x, y, z(x, y)) 0 F(x,y,z(x,y))0 🧠 目标: 求 ∂ z ∂ x \frac{\partial z}{\partial x} ∂x∂z、 …...

