Python获取最小路径,查找元素在list中的坐标
# coding=utf-8
__author__ = 'Jeff.xie'
def t(li):
pass
获取最小路径
def minPathSum(grid):
if not grid:
return 0
m= len(grid) #m列
n =len(grid[0]) #n行
print(grid[0])
print("m: ",m)
print("n: ",n)
#创建一个二维数组
dp = [[0]*n for _ in range(m)]
print(dp) #这是一个所有值为0的二维数组
dp[0][0] = grid[0][0]#初始化左上角
#初始化第一列,最小和只能从上面到达,且需要加上当前格子的元素值
for i in range(1,m):
dp[i][0] = dp[i-1][0]+grid[i][0]#每一行的第一个元素,得到结果,并且是从原始数据的每一行第一个数据一次累加
print(dp)
#初始化第一行,最小和只能从左边到达,且需要加加上当前格子元素的最小值
for i in range(1,n):
dp[0][i] = dp[0][i-1] + grid[0][i]
print(dp)
#遍历其他地方的格子,路径只能从相邻左方和相邻上方到达,然后比较两者中最小的元素值加上当前网格的值
for i in range(1,m):
for j in range(1,n):
dp[i][j] = min(dp[i-1][j],dp[i][j-1])+grid[i][j] #判断是上边dp[i-1][j]的数据小,还是左边dp[i][j-1]的数据小
print(dp)
return dp[-1][-1]
查找元素在list中的坐标
def searchRange( nums, target):
#在排序数组中查找元素的第一个和最后一个位置
left = -1
right = -1
for i in range(len(nums)):
if nums[i] == target:
left = i
break
if left != -1:
for i in range(left, len(nums)):
if nums[i] == target:
right = i
return [left, right]
def t5(grid):
#获取行和列
row=len(grid)
column = len(grid[0])
print(column)
#初始化一个全部值为0,但是行列都相同的li
li = [[0]*column for i in range(row)] #总共有len(row)行,每一行都是一个list,每个list的元素都赋值为0
print(li)
#初始化左上角
li[0][0]= grid[0][0]
#初始化第一列
for i in range(1,row):
li[i][0]=li[i-1][0]+grid[i][0]
print(li)
#初始化第一行
for i in range(1,column):
li[0][i]= li[0][i-1]+grid[0][i]
print(li)
#填充其他单元格
for i in range(1,row):
for j in range(1,column):
x= min(li[i-1][j],li[i][j-1])
li[i][j]= x+grid[i][j]
print(li)
#最后一个数字就是最小路径
return li[-1][-1]
if __name__ == '__main__':
grid = [[1,3,1],[1,5,1],[4,2,1],[2,3,4]]
# r= minPathSum(grid)
# print(r)
# r= t2(grid)
# print(r)
r3=t3(grid)
print("r3:",r3)
li=[1,2,3,4,5,5,6,7]
r=searchRange(li,6)
print(r)
t5(grid)
相关文章:

Python获取最小路径,查找元素在list中的坐标
# codingutf-8__author__ Jeff.xiedef t(li):pass获取最小路径def minPathSum(grid):if not grid:return 0m len(grid) #m列n len(grid[0]) #n行print(grid[0])print("m: ",m)print("n: ",n)#创建一个二维数组dp [[0]*n for _ in range(m)]print(dp) #这…...

数据采集协同架构,集成马扎克、西门子、海德汉、广数、凯恩帝、三菱、海德汉、兄弟、哈斯、宝元、新代、发那科、华中各类数控以及各类PLC数据采集软件
文章目录 前言一、采集协同架构是什么?可以做什么(数控、PLC配置采集)?二、使用步骤 1.打开软件,配置MQTT或者数据库(支持sqlserver、mysql等)存储转发消息规则2.配置数控系统所采集的参数、转…...
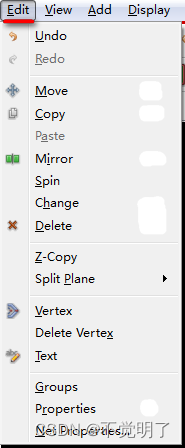
Allegro172版本如何用自带的功能实现快速在1MMBGA下方等距放置电容
Allegro172版本如何用自带的功能实现快速在1MMBGA下方等距放置电容 在做PCB设计的时候,在1MM中心间距的BGA背面放置电容,是非常常见的设计,如何快速把电容等距放在BGA下方,除了借助辅助工具外,在Allegro升级到了172版本的时候,可以借助本身自带的功能实现快速放置,以下图…...

一种简单的统计pytorch模型参数量的方法
nelememt()函数Tensor.nelement()->引自Tensor.numel()->引自torch.numel(input)三者的作用是相同的Returns the total number of elements in the inputtensor.返回当前tensor的元素数量利用上面的函数刚好可以统计模型的参数数量parameters()函数Module.parameters(rec…...

【PyTorch】教程:对抗学习实例生成
ADVERSARIAL EXAMPLE GENERATION 研究推动 ML 模型变得更快、更准、更高效。设计和模型的安全性和鲁棒性经常被忽视,尤其是面对那些想愚弄模型故意对抗时。 本教程将提供您对 ML 模型的安全漏洞的认识,并将深入了解对抗性机器学习这一热门话题。在图像…...

中国区使用Open AI账号试用Chat GPT指南
最近推出强大的ChatGPT功能,各大程序员使用后发出感叹:程序员要失业了 不过在国内并不支持OpenAI账号注册,多数会提示: OpenAI’s services are not available in your country. 经过一番搜索后,发现如下方案可以完…...
STM32开发(9)----CubeMX配置外部中断
CubeMX配置外部中断前言一、什么是中断1.STM32中断架构体系2.外部中断/事件控制器(EXTI)3.嵌套向量中断控制器(NIVC)二、实验过程1.CubeMX配置2.代码实现3.硬件连接4.实验结果总结前言 本章介绍使用STM32CubeMX对引脚的外部中断进…...
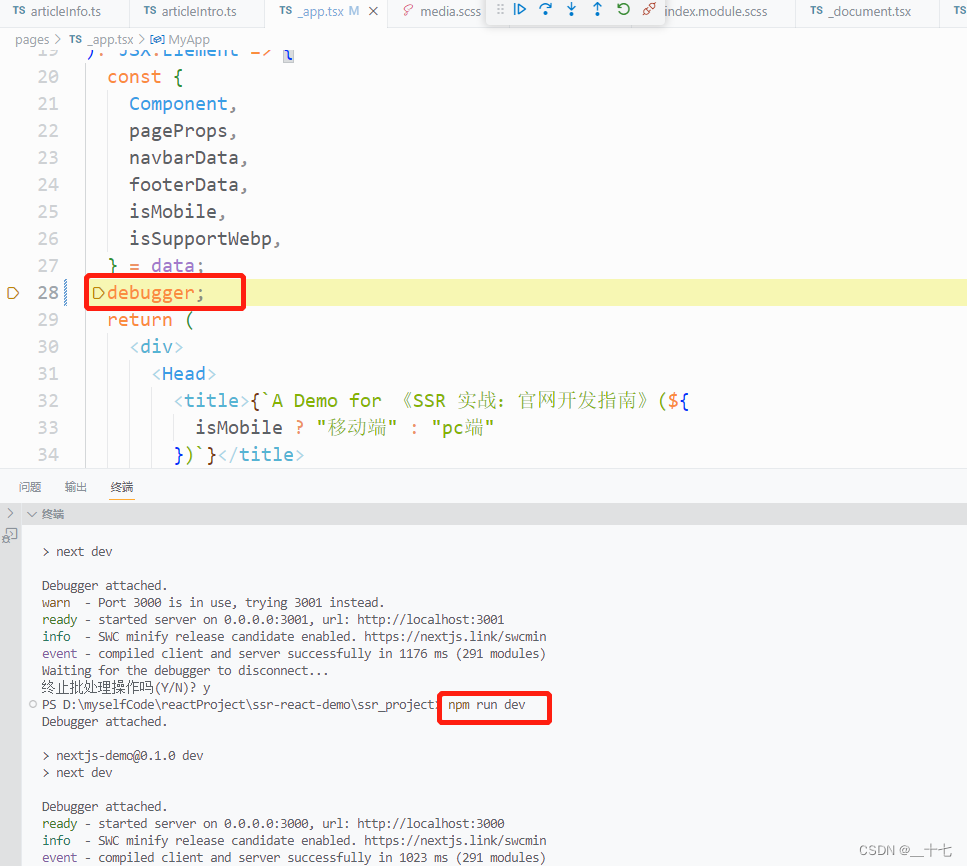
Nextjs了解内容
目录Next.jsnext.js的实现1,nextjs初始化2, 项目结构3, 数据注入getInitialPropsgetServerSidePropsgetStaticProps客户端注入3,CSS Modules4,layout组件5,文件式路由6,BFF层的文件式路由7&…...

从事功能测试1年,裸辞1个月,找不到工作的“我”怎么办?
做功能测试一年多了裸辞职一个月了,大部分公司都要求有自动化测试经验,可是哪来的自动化测试呢? 我要是简历上写了吧又有欺诈性,不写他们给的招聘又要自动化优先,将项目带向自动化不是一个容易的事情,很多…...

机器学习基本原理总结
本文大部分内容参考《深度学习》书籍,从中抽取重要的知识点,并对部分概念和原理加以自己的总结,适合当作原书的补充资料阅读,也可当作快速阅览机器学习原理基础知识的参考资料。 前言 深度学习是机器学习的一个特定分支。我们要想…...
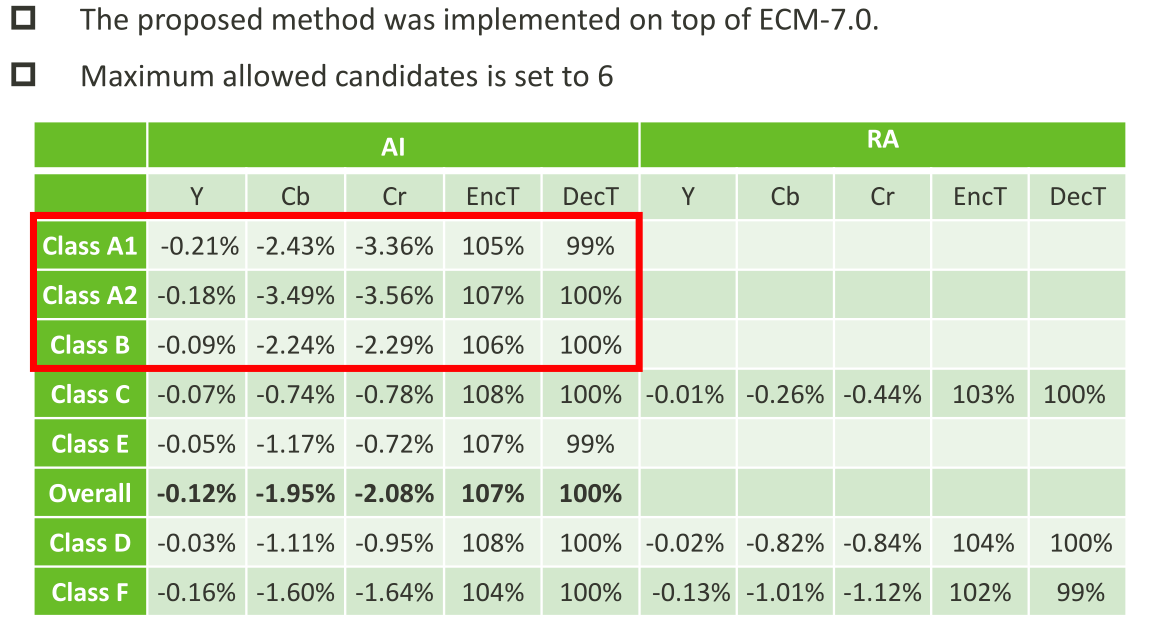
JVET-AC0315:用于色度帧内预测的跨分量Merge模式
ECM采用了许多跨分量的预测(Cross-componentprediction,CCP)模式,包括跨分量包括跨分量线性模型(CCLM)、卷积跨分量模型(CCCM)和梯度线性模型(GLM)࿰…...
)
Session与Cookie的区别(二)
脸盲症的困扰 小明身为杂货店的店长兼唯一的店员,所有大小事都是他一个人在处理。传统杂货店跟便利商店最大的差别在哪里?在于人情味。 就像是你去菜市场买菜的时候会被说帅哥或美女,或者是去买早餐的时候老板会问你:「一样&#…...
疫情开发,软件测试行情趋势是怎么样的?
如果说,2022年对于全世界来说,都是一场极大的挑战的话;那么,2023年绝对是机遇多多的一年。众所周知,随着疫情在全球范围内逐步得到控制,无论是国际还是国内的环境,都会呈现逐步回升的趋势&#…...

Java中间件描述与使用,面试可以用
myCat 用于切分mysql数据库(为什么要切分:当数据量过大时,mysql查询效率变低) ActiveMQ 订阅,消息推送 swagger 前后端分离,后台接口调式 dubbo 阿里的面向服务RPC框架,为什么要面向服务&#x…...

[OpenMMLab]AI实战营第七节课
语义分割代码实战教学 HRNet 高分辨率神经网络 安装配置 # 选择分支 git branch -a git switch 3.x # 配置环境 conda create -n mmsegmentation python3.8 conda activate mmsegmentation pip install torch1.11.0cu113 torchvision0.12.0cu113 torchaudio0.11.0 --extra-i…...
面向对象的设计模式
"万丈高楼平地起,7种模式打地基",模式是一种规范,我们应该站在巨人的肩膀上越看越远,接下来,让我们去仔细了解了解面向对象的7种设计模式7种设计模式设计原则的核心思想:找出应用中可能需要变化之…...

里氏替换原则|SOLID as a rock
文章目录 意图动机:违反里氏替换原则解决方案:C++中里氏替换原则的例子里氏替换原则的优点1、可兼容性2、类型安全3、可维护性在C++中用好LSP的标准费几句话本文是关于 SOLID as Rock 设计原则系列的五部分中的第三部分。 SOLID 设计原则侧重于开发 易于维护、可重用和可扩展…...

【C++】右左法则,指针、函数与数组
右左法则——判断复杂的声明对于一个复杂的声明,可以用右左法则判断它是个什么东西:1.先找到变量名称2.从变量名往右看一个部分,再看变量名左边的一个部分3.有小括号先看小括号里面的,一层一层往外看4.先看到的东西优先级大&#…...
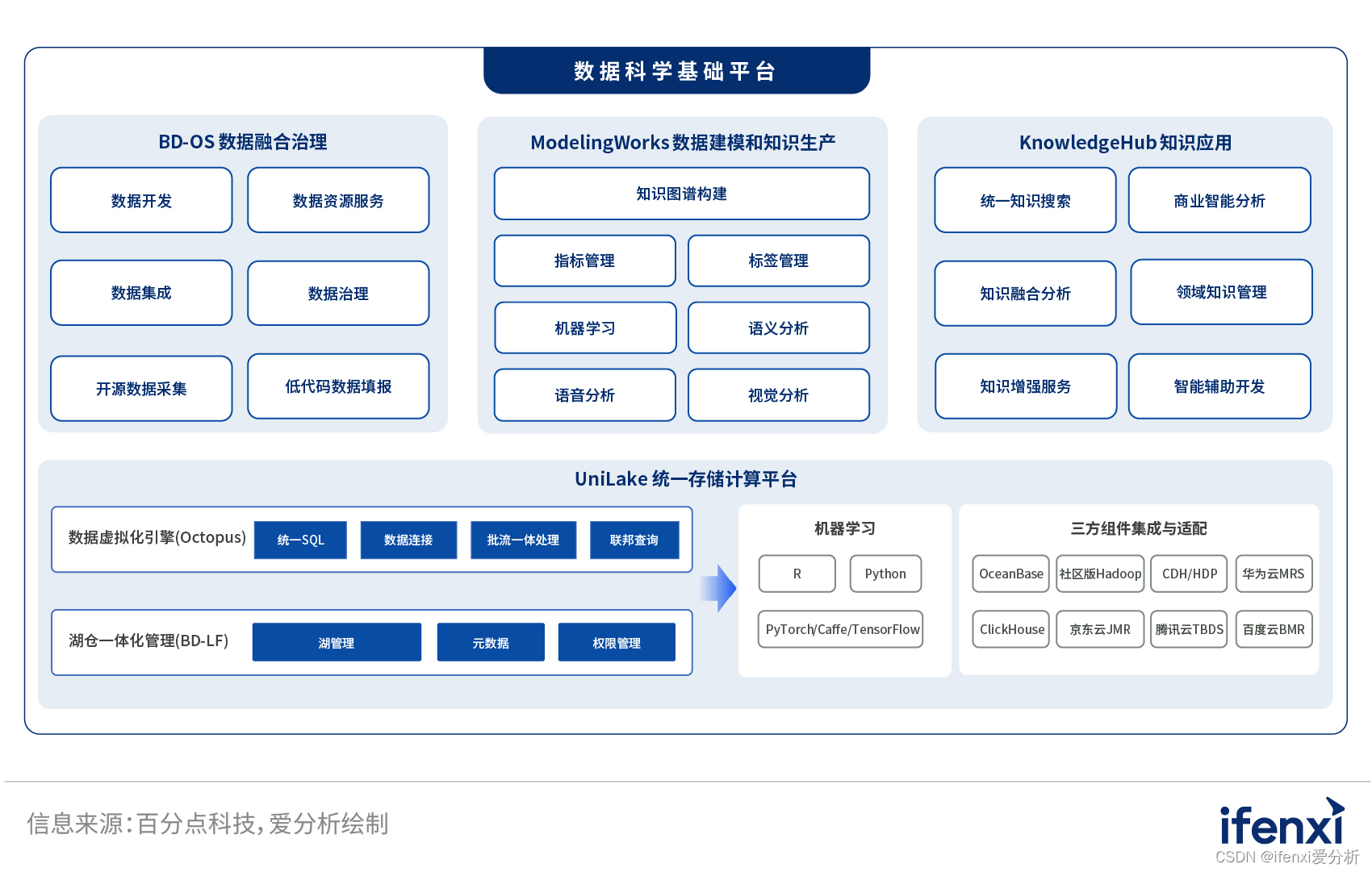
打通数据价值链,百分点数据科学基础平台实现数据到决策的价值转换 | 爱分析调研
随着企业数据规模的大幅增长,如何利用数据、充分挖掘数据价值,服务于企业经营管理成为当下企业数字化转型的关键。 如何挖掘数据价值?企业需要一步步完成数据价值链条的多个环节,如数据集成、数据治理、数据建模、数据分析、数据…...

C++之多态【详细总结】
前言 想必大家都知道面向对象的三大特征:封装,继承,多态。封装的本质是:对外暴露必要的接口,但内部的具体实现细节和部分的核心接口对外是不可见的,仅对外开放必要功能性接口。继承的本质是为了复用&#x…...

day52 ResNet18 CBAM
在深度学习的旅程中,我们不断探索如何提升模型的性能。今天,我将分享我在 ResNet18 模型中插入 CBAM(Convolutional Block Attention Module)模块,并采用分阶段微调策略的实践过程。通过这个过程,我不仅提升…...

dedecms 织梦自定义表单留言增加ajax验证码功能
增加ajax功能模块,用户不点击提交按钮,只要输入框失去焦点,就会提前提示验证码是否正确。 一,模板上增加验证码 <input name"vdcode"id"vdcode" placeholder"请输入验证码" type"text&quo…...

多模态商品数据接口:融合图像、语音与文字的下一代商品详情体验
一、多模态商品数据接口的技术架构 (一)多模态数据融合引擎 跨模态语义对齐 通过Transformer架构实现图像、语音、文字的语义关联。例如,当用户上传一张“蓝色连衣裙”的图片时,接口可自动提取图像中的颜色(RGB值&…...

学习STC51单片机31(芯片为STC89C52RCRC)OLED显示屏1
每日一言 生活的美好,总是藏在那些你咬牙坚持的日子里。 硬件:OLED 以后要用到OLED的时候找到这个文件 OLED的设备地址 SSD1306"SSD" 是品牌缩写,"1306" 是产品编号。 驱动 OLED 屏幕的 IIC 总线数据传输格式 示意图 …...

基于Docker Compose部署Java微服务项目
一. 创建根项目 根项目(父项目)主要用于依赖管理 一些需要注意的点: 打包方式需要为 pom<modules>里需要注册子模块不要引入maven的打包插件,否则打包时会出问题 <?xml version"1.0" encoding"UTF-8…...

全面解析各类VPN技术:GRE、IPsec、L2TP、SSL与MPLS VPN对比
目录 引言 VPN技术概述 GRE VPN 3.1 GRE封装结构 3.2 GRE的应用场景 GRE over IPsec 4.1 GRE over IPsec封装结构 4.2 为什么使用GRE over IPsec? IPsec VPN 5.1 IPsec传输模式(Transport Mode) 5.2 IPsec隧道模式(Tunne…...

AI书签管理工具开发全记录(十九):嵌入资源处理
1.前言 📝 在上一篇文章中,我们完成了书签的导入导出功能。本篇文章我们研究如何处理嵌入资源,方便后续将资源打包到一个可执行文件中。 2.embed介绍 🎯 Go 1.16 引入了革命性的 embed 包,彻底改变了静态资源管理的…...

企业如何增强终端安全?
在数字化转型加速的今天,企业的业务运行越来越依赖于终端设备。从员工的笔记本电脑、智能手机,到工厂里的物联网设备、智能传感器,这些终端构成了企业与外部世界连接的 “神经末梢”。然而,随着远程办公的常态化和设备接入的爆炸式…...

从 GreenPlum 到镜舟数据库:杭银消费金融湖仓一体转型实践
作者:吴岐诗,杭银消费金融大数据应用开发工程师 本文整理自杭银消费金融大数据应用开发工程师在StarRocks Summit Asia 2024的分享 引言:融合数据湖与数仓的创新之路 在数字金融时代,数据已成为金融机构的核心竞争力。杭银消费金…...

wpf在image控件上快速显示内存图像
wpf在image控件上快速显示内存图像https://www.cnblogs.com/haodafeng/p/10431387.html 如果你在寻找能够快速在image控件刷新大图像(比如分辨率3000*3000的图像)的办法,尤其是想把内存中的裸数据(只有图像的数据,不包…...
