数理统计的基本概念(二)
文章目录
- 抽样分布
- 几个重要分布
- 分位数
- 参考文献
抽样分布
所谓抽样分布是指统计量的概率分布。确定统计量的分布是数理统计学的基本问题之一。
几个重要分布
Γ \Gamma Γ 分布
若随机变量 X X X 具有概率密度 f ( x ; α , λ ) = { λ α Γ ( α ) x α − 1 e − λ x , x > 0 0 , x ≤ 0 f(x;\alpha,\lambda)=\begin{cases} \frac{\lambda^\alpha}{\Gamma(\alpha)}x^{\alpha-1}e^{-\lambda x}, &x>0 \\ 0, &x\le0 \end{cases} f(x;α,λ)={Γ(α)λαxα−1e−λx,0,x>0x≤0则称 X X X 服从参数为 α 、 λ \alpha、\lambda α、λ 的 Γ \Gamma Γ 分布,记为 X ∼ Γ ( α , λ ) X\sim \Gamma(\alpha, \lambda) X∼Γ(α,λ),其中 α > 0 , λ > 0 \alpha >0,\lambda >0 α>0,λ>0 为参数。
Γ \Gamma Γ 分布具有下列性质:
- 若 X ∼ Γ ( α , λ ) X\sim \Gamma(\alpha, \lambda) X∼Γ(α,λ),则 E ( X ) = α / λ , D ( x ) = α / λ 2 . E(X)=\alpha/\lambda, D(x)=\alpha/\lambda^2. E(X)=α/λ,D(x)=α/λ2.
- 可加性。若 X i ∼ Γ ( α i , λ ) , i = 1 , . . . , n X_i\sim \Gamma(\alpha_i, \lambda),i=1,...,n Xi∼Γ(αi,λ),i=1,...,n,且 X 1 , . . . , X n X_1,...,X_n X1,...,Xn 相互独立,则 X 1 + . . . + X n ∼ Γ ( α 1 + . . . + α n , λ ) X_1+...+X_n\sim\Gamma(\alpha_1+...+\alpha_n,\lambda) X1+...+Xn∼Γ(α1+...+αn,λ)
- 在 Γ \Gamma Γ 分布中取 α = 1 \alpha=1 α=1,即得指数分布 Exp ( λ ) \text{Exp}(\lambda) Exp(λ) f ( x ; λ ) = { λ e − λ x , x > 0 0 , x ≤ 0 f(x;\lambda)=\begin{cases} \lambda e^{-\lambda x}, &x>0 \\ 0, &x\le0 \end{cases} f(x;λ)={λe−λx,0,x>0x≤0 由此可得性质 2 的一个推论:若 X 1 , . . . , X n X_1,...,X_n X1,...,Xn 为 i.i.d. \text{i.i.d.} i.i.d.,且 X 1 ∼ Exp ( λ ) X_1\sim \text{Exp}(\lambda) X1∼Exp(λ),则 ∑ i = 1 n X i ∼ Γ ( n , λ ) \sum_{i=1}^nX_i \sim \Gamma(n,\lambda) i=1∑nXi∼Γ(n,λ)
β \beta β 分布
若随机变量 X X X 具有概率密度 f ( x ; a , b ) = { x a − 1 ( 1 − x ) b − 1 B ( a , b ) , 0 < x < 1 0 , 其他 f(x;a,b)=\begin{cases} \frac{x^{a-1}(1-x)^{b-1}}{B(a,b)}, &0<x<1 \\ 0, &其他 \end{cases} f(x;a,b)={B(a,b)xa−1(1−x)b−1,0,0<x<1其他则称 X X X 服从参数为 a 、 b a、b a、b 的 β \beta β 分布,记为 X ∼ β ( a , b ) X\sim \beta(a,b) X∼β(a,b),其中 a > 0 , b > 0 a >0,b >0 a>0,b>0 为参数, B ( a , b ) B(a,b) B(a,b) 为 β \beta β 函数。
β \beta β 分布具有下列性质:
- 若 X ∼ β ( a , b ) X\sim \beta(a,b) X∼β(a,b),则 E ( X ) = a a + b , D ( X ) = a b ( a + b ) 2 ( a + b + 1 ) E(X)=\frac{a}{a+b},D(X)=\frac{ab}{(a+b)^2(a+b+1)} E(X)=a+ba,D(X)=(a+b)2(a+b+1)ab
- 若 X ∼ Γ ( a , 1 ) , Y ∼ Γ ( b , 1 ) X\sim \Gamma(a,1),Y\sim \Gamma(b,1) X∼Γ(a,1),Y∼Γ(b,1),且 X , Y X,Y X,Y 相互独立,则 Z = X X + Y ∼ β ( a , b ) Z=\frac{X}{X+Y}\sim \beta(a,b) Z=X+YX∼β(a,b)
χ 2 \chi^2 χ2 分布
若随机变量 X X X 具有概率密度 χ 2 ( x ; n ) = { x n / 2 − 1 e − x / 2 2 n / 2 Γ ( n / 2 ) , x > 0 0 , x ≤ 0 \chi^2(x;n)=\begin{cases} \frac{x^{n/2-1}e^{-x/2}}{2^{n/2}\Gamma(n/2)}, &x>0 \\ 0, &x\le0 \end{cases} χ2(x;n)={2n/2Γ(n/2)xn/2−1e−x/2,0,x>0x≤0 则称 X X X 服从自由度为 n n n 的 χ 2 \chi^2 χ2 分布,记为 X ∼ χ 2 ( n ) X\sim \chi^2(n) X∼χ2(n)。
χ 2 \chi^2 χ2 分布具有下列性质:
- 若 X ∼ χ 2 ( n ) X\sim \chi^2(n) X∼χ2(n),则 E ( X ) = n , D ( X ) = 2 n E(X)=n,D(X)=2n E(X)=n,D(X)=2n
- 可加性。若 X i ∼ χ 2 ( n i ) , i = 1 , . . . , k X_i \sim \chi^2(n_i),i=1,...,k Xi∼χ2(ni),i=1,...,k,且 X 1 , . . . , X k X_1,...,X_k X1,...,Xk 相互独立,则 X 1 + . . . + X n ∼ χ 2 ( n 1 + . . . + n k ) X_1+...+X_n\sim \chi^2(n_1+...+n_k) X1+...+Xn∼χ2(n1+...+nk)
设随机变量 X 1 , . . . , X n X_1,...,X_n X1,...,Xn 相互独立,且都服从标准正态分布 N ( 0 , 1 ) N(0,1) N(0,1),则随机变量 χ 2 = ∑ i = 1 n X i 2 \chi^2=\sum_{i=1}^n X_i^2 χ2=∑i=1nXi2 服从自由度为 n n n 的 χ 2 \chi^2 χ2 分布。
t t t 分布
t t t 分布又称学生分布,随机变量 T T T 服从自由度为 n n n 的 t t t 分布记为 T ∼ t ( n ) T\sim t(n) T∼t(n)。
t t t 分布的概率密度关于 x = 0 x=0 x=0 对称,并且当 ∣ x ∣ → + ∞ |x|\to +\infty ∣x∣→+∞ 时单调下降地趋于 0,且当自由度 n → + ∞ n\to +\infty n→+∞ 时,自由度为 n n n 的 t t t 分布收敛于标准正态分布 N ( 0 , 1 ) N(0,1) N(0,1)。
若 X ∼ N ( 0 , 1 ) , Y ∼ χ 2 ( n ) X\sim N(0,1),Y\sim \chi^2(n) X∼N(0,1),Y∼χ2(n),且 X X X 与 Y Y Y相互独立,则 T = X Y / n ∼ t ( n ) T=\frac{X}{\sqrt{Y/n}}\sim t(n) T=Y/nX∼t(n)
F F F 分布
随机变量 F F F 服从自由度为 ( n 1 , n 2 ) (n_1,n_2) (n1,n2) 的 F F F 分布记为 F ∼ F ( n 1 , n 2 ) F\sim F(n_1,n_2) F∼F(n1,n2)。
若 X ∼ χ 2 ( n 1 ) , Y ∼ χ 2 ( n 2 ) X\sim \chi^2(n_1),Y\sim \chi^2(n_2) X∼χ2(n1),Y∼χ2(n2),且 X X X 与 Y Y Y相互独立,则 F = X / n 1 Y / n 2 ∼ F ( n 1 , n 2 ) F=\frac{X/n_1}{Y/n_2} \sim F(n_1,n_2) F=Y/n2X/n1∼F(n1,n2)
在上述定理的条件下,若 F ∼ F ( n 1 , n 2 ) F\sim F(n_1,n_2) F∼F(n1,n2),则 1 F ∼ F ( n 2 , n 1 ) \frac{1}{F} \sim F(n_2,n_1) F1∼F(n2,n1)。
分位数
设随机变量 X X X 的分布函数为 F ( x ) = P ( X ≤ x ) F(x)=P(X\le x) F(x)=P(X≤x),对于 0 < p < 1 0<p<1 0<p<1,若有 x p x_p xp 满足 P ( X ≤ x p ) = F ( x p ) = p P(X\le x_p)=F(x_p)=p P(X≤xp)=F(xp)=p 则称 x p x_p xp 为分布 F ( x ) F(x) F(x) (或随机变量 X X X)的下侧 p p p 分位数;对于 0 < α < 1 0<\alpha <1 0<α<1,若有 y α y_\alpha yα 满足 P ( X > y α ) = 1 − F ( y α ) = α P(X>y_\alpha)=1-F(y_\alpha)=\alpha P(X>yα)=1−F(yα)=α 则称 y α y_\alpha yα 为分布 F ( x ) F(x) F(x) (或随机变量 X X X)的上侧 α \alpha α 分位数。
由定义可知, y α = x 1 − α ; x p = y 1 − p y_\alpha=x_{1-\alpha}; x_p=y_{1-p} yα=x1−α;xp=y1−p。
- 由 N ( 0 , 1 ) N(0,1) N(0,1) 分布及 t t t 分布的对称性可知 u 1 − α = − u α , t 1 − α ( n ) = − t α ( n ) u_{1-\alpha}=-u_\alpha,t_{1-\alpha}(n)=-t_\alpha(n) u1−α=−uα,t1−α(n)=−tα(n)
- F α ( n 1 , n 2 ) = 1 F 1 − α ( n 2 , n 1 ) F_\alpha(n_1,n_2)=\frac{1}{F_{1-\alpha}(n_2,n_1)} Fα(n1,n2)=F1−α(n2,n1)1
参考文献
[1] 《应用数理统计》,施雨,西安交通大学出版社。
相关文章:
)
数理统计的基本概念(二)
文章目录 抽样分布几个重要分布 Γ \Gamma Γ 分布 β \beta β 分布 χ 2 \chi^2 χ2 分布 t t t 分布 F F F 分布 分位数 参考文献 抽样分布 所谓抽样分布是指统计量的概率分布。确定统计量的分布是数理统计学的基本问题之一。 几个重要分布 Γ \Gamma Γ 分布 若随机变量 …...

CountDownLatch和CyclicBarrier
JUC(Java.util.concurrent)是Java 5中引入的一个并发编程库,它包含了许多用于多线程处理的工具类和接口。JUC主要提供了以下特性: 线程池:线程池可以提高线程的使用效率,避免频繁地创建和销毁线程ÿ…...

云原生正在重塑软件的整个生命周期(内附资料)
随着企业数字化转型进程的发展,企业面临着新旧商业形态的剧变,颠覆和重构时刻都在发生。 企业需要更加快速地感知用户侧的需求变化并做出调整,才有可能在竞争中持续积累优势。业务的个性化、敏捷化、智能化需求日益突显,数字化应…...
Node.js环境配置级安装vue-cli脚手架
一、下载安装Node.js (略) 二、验证node.js并配置 1、下载安装后,cmd面板输入node -v查询版本、npm -v ,查看npm是否安装成功(有版本号就行了) 2、选择npm镜像(npm config set registry https://registry.npm.taobao.org&…...

十七、Rust集成MQTT Client
1、信息整理 目前了解到的Rust MQTT项目有: bytebeamio/rumqtt 1.3k star、717 commits、Contributors 78、tokio、futures、tls、rumqttc(client):cargo add rumqttc https://github.com/bytebeamio/rumqtt/tree/main/rumqttc ru…...
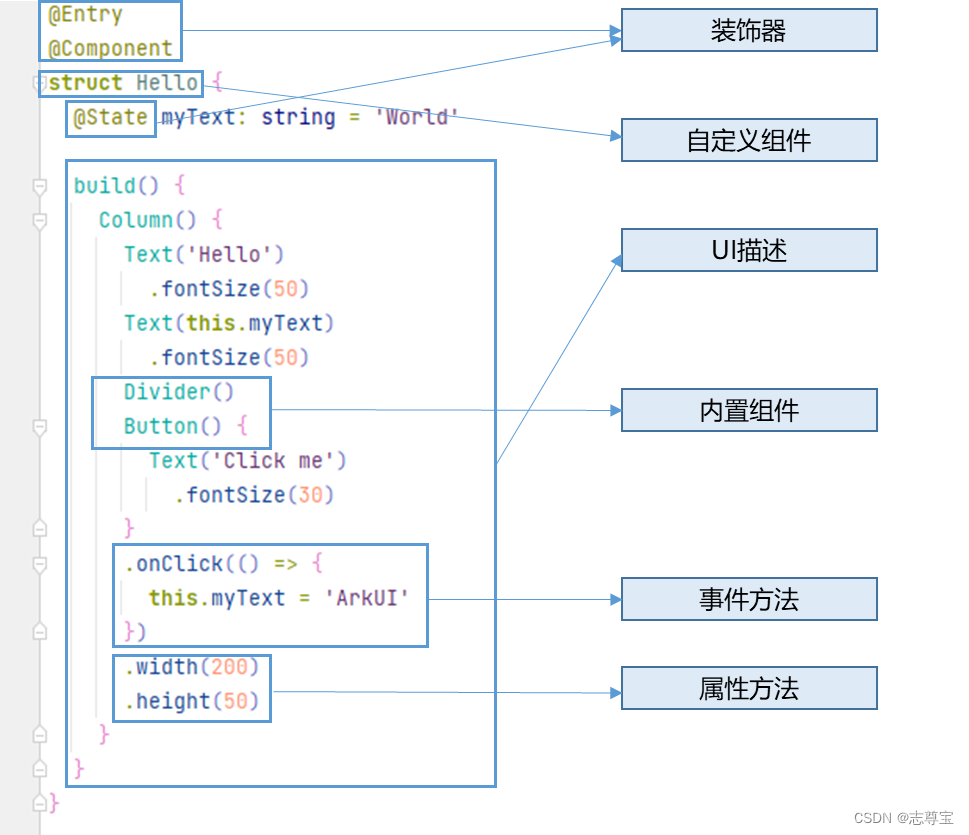
HarmonyOS ArkTS开发语言介绍(三)
1 引言 Mozilla创造了JS,Microsoft创建了TS,Huawei进一步推出了ArkTS。 从最初的基础的逻辑交互能力,到具备类型系统的高效工程开发能力,再到融合声明式UI、多维状态管理等丰富的应用开发能力,共同组成了相关的演进脉…...
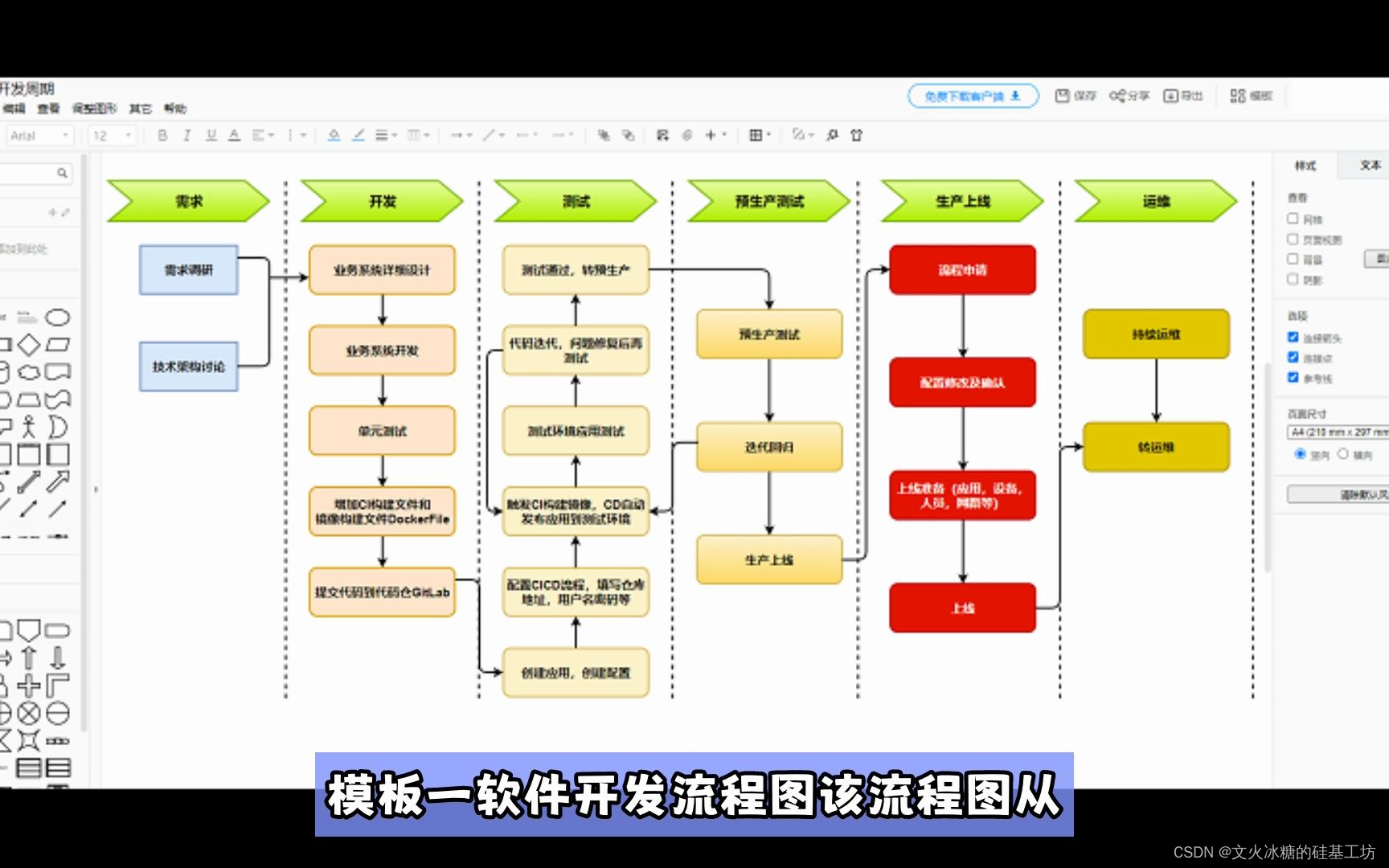
[架构之路-247]:目标系统 - 设计方法 - 软件工程 - 结构化方法的基本思想、本质、特点以及在软件开发、在生活中的应用
目录 前言: 一、什么是非结构化方法 1.1 什么是非结构化方法 1.2 非结构化方法的适用场合 二、什么是结构化方法 1.1 结构化方法诞生的背景:软件规模发展:大规模、复杂系统的需要 1.2 概述 1.3 主要特点与核心思想 三、结构化方法在…...
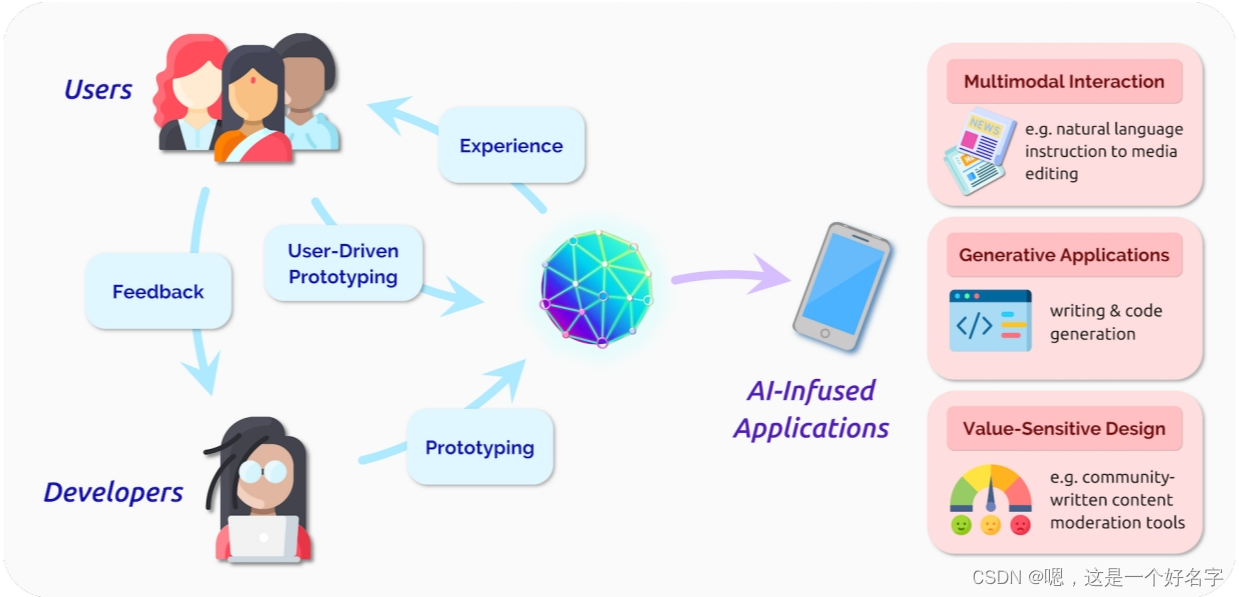
大模型的交互能力
摘要: 基础大模型显示出明显的潜力,可以改变AI系统的开发人员和用户体验:基础模型降低了原型设计和构建AI应用程序的难度阈值,因为它们在适应方面的样本效率,并提高了新用户交互的上限,因为它们的多模式和生…...

80%测试员被骗,关于jmeter 的一个弥天大谎!
jmeter是目前大家都喜欢用的一款性能测试工具,因为它小巧、简单易上手,所以很多人都愿意用它来做接口测试或者性能测试,因此,在目前企业中,使用各个jmeter的版本都有,其中以jmeter3.x、4.x的应该居多。 但是…...
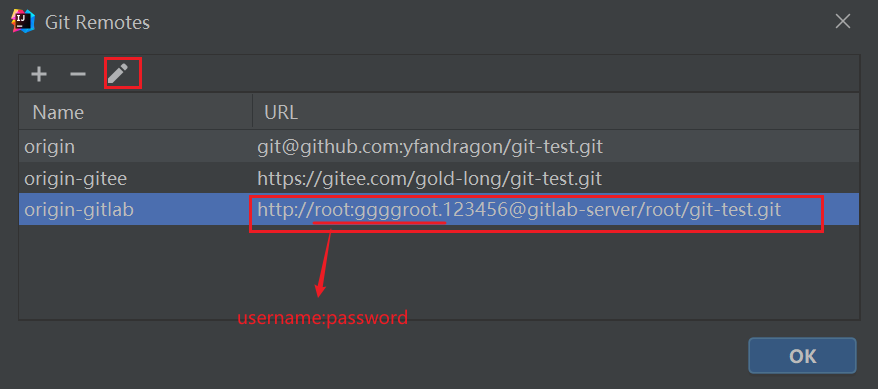
Git——感谢尚硅谷官方文档
Git——尚硅谷学习笔记 第1章 Git 概述1.1 何为版本控制1.2 为什么需要版本控制1.3 版本控制工具1.4 Git 简史1.5 Git 工作机制1.6 Git 和代码托管中心 第2章 Git 安装第 3 章 Git 常用命令3.1 设置用户签名3.2 初始化本地库3.3 查看本地库状态3.4 添加暂存区3.4.1 将工作区的文…...

Java WebSocket框架
引言 随着互联网和移动互联网的迅猛发展,实时通信成为了应用程序的一项重要能力。WebSocket作为一种在Web上实现双向通信的协议,极大地丰富了Web应用程序的交互方式。而在Java领域,也有许多优秀的WebSocket框架可供选择,本文将介…...

C#实现本地服务器客户端私聊通信
(一)需求 在游戏中我们经常能够看到玩家与玩家之间可以进行私聊,在QQ或微信中最基本的功能就是用户与用户之间的通信。抽象成计算机网络,就是两个客户端通过服务器进行私聊通信,两个客户端可以互相看到对方发送过来的信…...

PyTorch 之 Dataset 类入门学习
PyTorch 之 Dataset 类入门学习 Dataset 类简介 PyTorch 中的 Dataset 类是一个抽象类,用来表示数据集。通过继承 Dataset 类可以进行自定义数据集的格式、大小和其它属性,供后续使用; 可以看到官方封装好的数据集也是直接或间接的继承自 …...

Java update scheduler
引言 Java 更新调度器是 Java 中的一个特性,可以自动化 Java 应用程序的更新过程。它提供了一种方便的方式来安排 Java 应用程序的更新,确保其与最新的功能、错误修复和安全补丁保持同步。本文将深入介绍如何使用 Java 更新调度器,并解释它对…...

常见树种(贵州省):006栎类
摘要:本专栏树种介绍图片来源于PPBC中国植物图像库(下附网址),本文整理仅做交流学习使用,同时便于查找,如有侵权请联系删除。 图片网址:PPBC中国植物图像库——最大的植物分类图片库 一、麻栎 …...
拓扑排序-
有向无环图是拓扑排序 拓扑排序将图中所有的顶点排成一个线性序列,使得所有的有向边均从序列的前面指向后面。 拓扑排序使用深度优先搜索来实现,图中有环则无法进行拓扑排序 一个有向图,如果图中有入度为0的点,就把这个点删掉…...

Oracle数据库如何定位trace file位置
用一个示例来说明吧。 在导入master key时,出现错误: ADMINISTER KEY MANAGEMENTIMPORT KEYS WITH SECRET "my_secret"FROM /tmp/export.expIDENTIFIED BY keypwd5 WITH BACKUP; ADMINISTER KEY MANAGEMENT * ERROR at line 1: ORA-46655…...
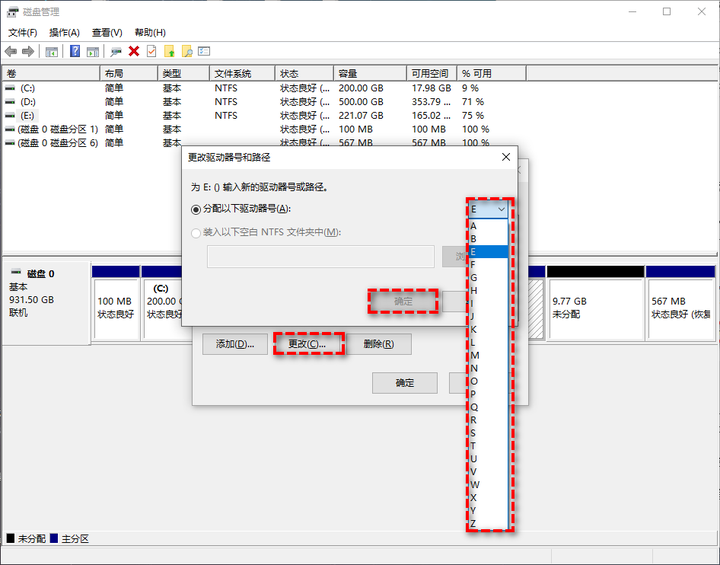
电脑盘符错乱,C盘变成D盘怎么办?
在一些特殊情况下,磁盘盘符会出现错乱,C盘可能会变成D盘。那么,这该怎么办呢?下面我们就来了解一下。 通过磁盘管理更改盘符 磁盘管理是Windows自带的工具,它位于“计算机管理”的控制台中。管理硬盘及其所包含的卷或…...
)
Android WMS——客户端输入事件处理(十九)
前面的文章我们介绍了 WMS 中的输入服务的启动及事件处理,这一篇我们来看一下客户端对输入事件的处理。 一、事件初始化 事件的初始化就是在添加窗口的过程。 1、ViewRootImpl 源码位置:/frameworks/base/core/java/android/view/ViewRootImpl.java public void setView(…...

Python基础学习__测试报告
# 使用pycharm生成报告:只有在单独执行一个TestCase文件时可以生成,使用TestSuite等就不能用了 # 使用第三方的测试报告:例如:HTMLTestRunner第三方类库 #使用HTMLTestRunner这个执行对象# 1.获取第三方的测试运行类Runner模块(一个py文件),将其放在代码目录下 # 2.导包:unitte…...

2024年赣州旅游投资集团社会招聘笔试真
2024年赣州旅游投资集团社会招聘笔试真 题 ( 满 分 1 0 0 分 时 间 1 2 0 分 钟 ) 一、单选题(每题只有一个正确答案,答错、不答或多答均不得分) 1.纪要的特点不包括()。 A.概括重点 B.指导传达 C. 客观纪实 D.有言必录 【答案】: D 2.1864年,()预言了电磁波的存在,并指出…...

蓝牙 BLE 扫描面试题大全(2):进阶面试题与实战演练
前文覆盖了 BLE 扫描的基础概念与经典问题蓝牙 BLE 扫描面试题大全(1):从基础到实战的深度解析-CSDN博客,但实际面试中,企业更关注候选人对复杂场景的应对能力(如多设备并发扫描、低功耗与高发现率的平衡)和前沿技术的…...

ESP32 I2S音频总线学习笔记(四): INMP441采集音频并实时播放
简介 前面两期文章我们介绍了I2S的读取和写入,一个是通过INMP441麦克风模块采集音频,一个是通过PCM5102A模块播放音频,那如果我们将两者结合起来,将麦克风采集到的音频通过PCM5102A播放,是不是就可以做一个扩音器了呢…...

Linux-07 ubuntu 的 chrome 启动不了
文章目录 问题原因解决步骤一、卸载旧版chrome二、重新安装chorme三、启动不了,报错如下四、启动不了,解决如下 总结 问题原因 在应用中可以看到chrome,但是打不开(说明:原来的ubuntu系统出问题了,这个是备用的硬盘&a…...
可以参考以下方法:)
根据万维钢·精英日课6的内容,使用AI(2025)可以参考以下方法:
根据万维钢精英日课6的内容,使用AI(2025)可以参考以下方法: 四个洞见 模型已经比人聪明:以ChatGPT o3为代表的AI非常强大,能运用高级理论解释道理、引用最新学术论文,生成对顶尖科学家都有用的…...

优选算法第十二讲:队列 + 宽搜 优先级队列
优选算法第十二讲:队列 宽搜 && 优先级队列 1.N叉树的层序遍历2.二叉树的锯齿型层序遍历3.二叉树最大宽度4.在每个树行中找最大值5.优先级队列 -- 最后一块石头的重量6.数据流中的第K大元素7.前K个高频单词8.数据流的中位数 1.N叉树的层序遍历 2.二叉树的锯…...

使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台
🎯 使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台 📌 项目背景 随着大语言模型(LLM)的广泛应用,开发者常面临多个挑战: 各大模型(OpenAI、Claude、Gemini、Ollama)接口风格不统一;缺乏一个统一平台进行模型调用与测试;本地模型 Ollama 的集成与前…...

Selenium常用函数介绍
目录 一,元素定位 1.1 cssSeector 1.2 xpath 二,操作测试对象 三,窗口 3.1 案例 3.2 窗口切换 3.3 窗口大小 3.4 屏幕截图 3.5 关闭窗口 四,弹窗 五,等待 六,导航 七,文件上传 …...

Python 实现 Web 静态服务器(HTTP 协议)
目录 一、在本地启动 HTTP 服务器1. Windows 下安装 node.js1)下载安装包2)配置环境变量3)安装镜像4)node.js 的常用命令 2. 安装 http-server 服务3. 使用 http-server 开启服务1)使用 http-server2)详解 …...

在 Spring Boot 中使用 JSP
jsp? 好多年没用了。重新整一下 还费了点时间,记录一下。 项目结构: pom: <?xml version"1.0" encoding"UTF-8"?> <project xmlns"http://maven.apache.org/POM/4.0.0" xmlns:xsi"http://ww…...
