如何证明特征值的几何重数不超过代数重数
设 λ 0 \lambda_0 λ0 是 A A A 的特征值,则 λ 0 \lambda_0 λ0 的代数重数 ≥ \geq ≥ 几何重数
证明
假设 A A A 的特征值 λ 0 \lambda_0 λ0 对应的特征向量有 q 维,记为 α 1 , . . . , α q \alpha_1, ... , \alpha_q α1,...,αq,有
A α i = λ 0 α i , i = 1 , . . . , q A\alpha_i = \lambda_0\alpha_i, i = 1, ... , q Aαi=λ0αi,i=1,...,q
以它们作为 n 维向量空间的 q q q 个基底向量,再扩充它们,将 n 维向量空间的整个基表示为 α 1 , . . . , α q , . . . , α n \alpha_1, ..., \alpha_q, ... , \alpha_n α1,...,αq,...,αn.
记矩阵 B = [ α 1 , . . . , α q , . . . α n ] B=[\alpha_1, ..., \alpha_q,... \alpha_n] B=[α1,...,αq,...αn] ,有 B B B 可逆。
A B = A [ α 1 , . . , α q , . . . , α n ] = [ λ 0 α 1 , . . . , λ 0 α q , . . . , A α n ] = [ α 1 , . . , α q , . . . , α n ] [ λ 0 ⋯ 0 ∗ ⋯ ∗ ⋮ ⋱ ⋮ ⋮ ⋮ 0 ⋯ λ 0 ∗ ⋯ ∗ 0 ⋯ 0 ∗ ⋯ ∗ ⋮ ⋮ ⋮ ⋮ 0 ⋯ 0 ∗ ⋯ ∗ ] A B = B [ λ 0 E A 12 O A 22 ] \begin{align*} AB &= A\begin{bmatrix} \alpha_1,..,\alpha_q,...,\alpha_n \end{bmatrix}= \begin{bmatrix} \lambda_0\alpha_1,...,\lambda_0\alpha_q,...,A\alpha_n \end{bmatrix}\\ &= \begin{bmatrix} \alpha_1,..,\alpha_q,...,\alpha_n \end{bmatrix} \begin{bmatrix} \lambda_0 & \cdots & 0 & * & \cdots & *\\ \vdots & \ddots & \vdots & \vdots & & \vdots \\ 0 & \cdots & \lambda_0 & * & \cdots & *\\ 0 & \cdots & 0 & * & \cdots & *\\ \vdots & & \vdots & \vdots & & \vdots \\ 0 & \cdots &0 & * & \cdots & *\\ \end{bmatrix}\\ AB&= B \begin{bmatrix} \lambda_0E & A_{12} \\ \mathcal{O} & A_{22} \end{bmatrix} \end{align*} ABAB=A[α1,..,αq,...,αn]=[λ0α1,...,λ0αq,...,Aαn]=[α1,..,αq,...,αn] λ0⋮00⋮0⋯⋱⋯⋯⋯0⋮λ00⋮0∗⋮∗∗⋮∗⋯⋯⋯⋯∗⋮∗∗⋮∗ =B[λ0EOA12A22]
又B可逆,则
B − 1 A B = [ λ 0 E A 12 O A 22 ] = C B^{-1}AB = \begin{bmatrix} \lambda_0E & A_{12} \\ \mathcal{O} & A_{22} \end{bmatrix} = C B−1AB=[λ0EOA12A22]=C
即 A A A 相似于 C
由此计算 A A A 的特征多项式
∣ λ E − A ∣ = ∣ λ E − C ∣ = ∣ ( λ − λ 0 ) E q − A 12 O λ E n − q − A 22 ∣ = ∣ ( λ − λ 0 ) q ∣ λ E n − q − A 22 ∣ |\lambda E-A| = |\lambda E - C| =\left | \begin{matrix} (\lambda - \lambda_0) E_q & - A_{12} \\ \mathcal{O} & \lambda E_{n-q} - A_{22} \\ \end{matrix} \right | =|(\lambda - \lambda_0)^q |\lambda E_{n-q} - A_{22}| ∣λE−A∣=∣λE−C∣= (λ−λ0)EqO−A12λEn−q−A22 =∣(λ−λ0)q∣λEn−q−A22∣
由此可知该 λ \lambda λ 的n次多项式方程至少有 q 个根为 λ 0 \lambda_0 λ0,至于有没有更多的根为 λ 0 \lambda_0 λ0,取决于后面的多项式 ∣ λ E n − q − A 22 ∣ |\lambda E_{n-q} - A_{22}| ∣λEn−q−A22∣ 是否出现 ( λ − λ 0 ) (\lambda - \lambda_0) (λ−λ0)。
相关文章:

如何证明特征值的几何重数不超过代数重数
设 λ 0 \lambda_0 λ0 是 A A A 的特征值,则 λ 0 \lambda_0 λ0 的代数重数 ≥ \geq ≥ 几何重数 证明 假设 A A A 的特征值 λ 0 \lambda_0 λ0 对应的特征向量有 q 维,记为 α 1 , . . . , α q \alpha_1, ... , \alpha_q α1,...,…...

Android修行手册-POI操作Excel文档
Unity3D特效百例案例项目实战源码Android-Unity实战问题汇总游戏脚本-辅助自动化Android控件全解手册再战Android系列Scratch编程案例软考全系列Unity3D学习专栏蓝桥系列ChatGPT和AIGC 👉关于作者 专注于Android/Unity和各种游戏开发技巧,以及各种资源分…...

浅析教学型数控车床使用案例
教学型数控车床是一种专为教学和培训设计的机床,它具有小型化、高精度和灵活性的特点,可以作为学校和技术学院的培训机器。下面是一个使用案例,以展示教学型数控车床在教学实训中的应用。 案例背景: 某职业技术学院的机械工程专业…...

图论 2023.11.20
次短路 P2829 大逃离 题意:给定一个无向图,入口1,出口n,求第二短路的值 一个节点所直接连接的地方小于k个(起点和终点除外),那么他就不敢进去。 n<5000,m<100000 思路:次短路…...
思福迪 运维安全管理系统 test_qrcode_b 远程命令执行漏洞
思福迪 运维安全管理系统 test_qrcode_b 远程命令执行漏洞 一、漏洞描述二、漏洞影响三、网络测绘四、漏洞复现1.手动复现2.自动化复现3.python源代码 免责声明:请勿利用文章内的相关技术从事非法测试,由于传播、利用此文所提供的信息或者工具而造成的任…...

electron项目开机自启动
一、效果展示:界面控制是否需要开机自启动 二、代码实现: 1、在渲染进程login.html中,画好界面,默认勾选; <div class"intro">开机自启动 <input type"checkbox" id"checkbox&quo…...

2023年约特干故城夜间演艺《万方乐奏有于阗》完美谢幕
11月19日,记者走进约特干故城看到演员在欢乐地跳着刀郎舞和古典舞,庆祝今年以来夜间演艺《万方乐奏有于阗》演出200场完美谢幕。 11月19日在约特干故城,演员正在表演迎宾乐舞。阿卜力克木依卜拉依木摄 当天晚上,城楼上旌旗猎猎&am…...
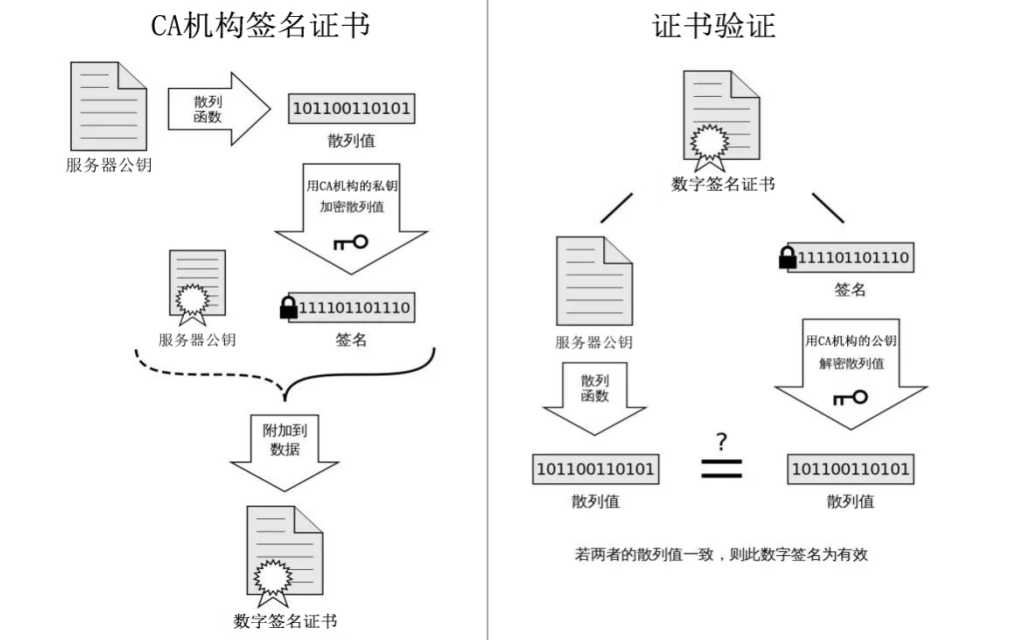
学习网络编程No.10【深入学习HTTPS】
引言: 北京时间:2023/11/14/18:45,因为种种原因,上个月的文章昨天才更新,目前处于刷题前夕,算法课在看了。这次和以前不一样,因为以前对知识框架没有很好的理念,并不清楚相关知识要…...
ubuntu下docker环境使用GPU配置
本文主要讲述整个命令流程,具体讲解请看官网nvidia-容器工具包和一篇总结得很详细的博文docker使用GPU总结 docker的版本必须安装19.0版本以上的,这里也只讲19.0版本以上的使用方法 首先设置一下网络信息 curl -fsSL https://nvidia.github.io/libnvi…...

渗透工具---BurpSuite 插件开发之HelloWorld
本文主要记录如何利用burp官方的新版API即MontoyaApi 写helloworld(上一篇的demo使用旧版api写的,这篇及后续开发将采用新版api) 先看效果图 更多详细内容见下方 这里有更详细更全面的代码内容 以及配置相关的内容 https://mp.weixin.qq.co…...

2216. 美化数组的最少删除数
我的做法: 使用一个index作为检查坐标,当index为偶数时检查当前数和后一个数是否相等,相等的话,后一个数设置为-1,注意如果相等,要把相等的数保留下来last,以便接下来检查,防止出现2…...

竞赛 题目:基于深度学习的人脸表情识别 - 卷积神经网络 竞赛项目 代码
文章目录 0 简介1 项目说明2 数据集介绍:3 思路分析及代码实现3.1 数据可视化3.2 数据分离3.3 数据可视化3.4 在pytorch下创建数据集3.4.1 创建data-label对照表3.4.2 重写Dataset类3.4.3 数据集的使用 4 网络模型搭建4.1 训练模型4.2 模型的保存与加载 5 相关源码6…...

基于安卓android微信小程序的好物分享系统
运行环境 开发语言:Java 框架:ssm JDK版本:JDK1.8 服务器:tomcat7 数据库:mysql 5.7(一定要5.7版本) 数据库工具:Navicat11 开发软件:eclipse/myeclipse/idea Maven包&a…...
【Spring Boot】使用WebSocket协议完成来单提醒及客户催单功能
1 WebSocket介绍 WebSocket 是基于 TCP 的一种新的网络协议。它实现了浏览器与服务器全双工通信(双向传输)——浏览器和服务器只需要完成一次握手,两者之间就可以创建持久性的连接, 并进行双向数据传输。 1.1 HTTP协议和WebSocket协议对比 1、HTTP是短…...

如何有效的禁止Google Chrome自动更新?
禁止Chrome自动更新 1、背景2、操作步骤 1、背景 众所周知,当我们在使用Selenium进行Web自动化操作(如爬虫)时,一般会用到ChromeDriver。然而Driver的更新速度明显跟不上Chrome的自动更新。导致我们在使用Selenium进行一些操作时就…...

OpenShift 4 - 部署 RHODS 环境,运行 AI/ML 应用(视频)
《OpenShift / RHEL / DevSecOps 汇总目录》 说明:本文已经在 OpenShift 4.14 RHODS 1.33 的环境中验证 文章目录 RHODS 简介安装 RHODS 环境运行环境说明用 RHODS Operator 安装环境创建 Jupyter Notebook 运行环境 开发调式 AI/ML 应用部署运行 AI/ML 应用视频参…...

MySQL 的执行原理(二)
5.3. MySQL 的查询成本 5.3. MySQL 的查询成本 MySQL 执行一个查询可以有不同的执行方案,它会选择其中成本最低,或者 说代价最低的那种方案去真正的执行查询。不过我们之前对成本的描述是非常模 糊的,其实在 MySQL 中一条查询语句的执行成本…...
 和 =any(?) 用法/性能对比)
postgres in (?,?) 和 =any(?) 用法/性能对比
刚刚回顾了一下 JDBC 操作 SQL Server 时如何传入列表参数,即如何给 in (?) 条件直接传入一个列表参数,然而本质上是不支持,最终不得不展开为 in (?, ?,...?) 针对每个元素单独设置参数,不定长的参数对于重用已编译 PreparedS…...

46. Qt Android调用Java代码进行辅助开发 -- 框架搭建
1. 说明 使用Qt进行android开发时,某种情况下使用C++的知识或者Qt提供的方法是无法满足功能需求的,即使通过各种手段能够勉强实现功能,也非常的麻烦。此时,就需要Java来辅助实现了。在Qt中提供了调用Java代码的接口,比较方便。本片博客先介绍如何搭建一个能够调用java代码…...

NX二次开发UF_CAM_PREF_set_logical_value 函数介绍
文章作者:里海 来源网站:https://blog.csdn.net/WangPaiFeiXingYuan UF_CAM_PREF_set_logical_value Defined in: uf_cam_prefs.h int UF_CAM_PREF_set_logical_value(UF_CAM_PREF_t pref, logical value ) overview 概述 This function sets the lo…...

stm32G473的flash模式是单bank还是双bank?
今天突然有人stm32G473的flash模式是单bank还是双bank?由于时间太久,我真忘记了。搜搜发现,还真有人和我一样。见下面的链接:https://shequ.stmicroelectronics.cn/forum.php?modviewthread&tid644563 根据STM32G4系列参考手…...

2.Vue编写一个app
1.src中重要的组成 1.1main.ts // 引入createApp用于创建应用 import { createApp } from "vue"; // 引用App根组件 import App from ./App.vue;createApp(App).mount(#app)1.2 App.vue 其中要写三种标签 <template> <!--html--> </template>…...

macOS多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用
文章目录 问题现象问题原因解决办法 问题现象 macOS启动台(Launchpad)多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用。 问题原因 很明显,都是Google家的办公全家桶。这些应用并不是通过独立安装的…...

【Web 进阶篇】优雅的接口设计:统一响应、全局异常处理与参数校验
系列回顾: 在上一篇中,我们成功地为应用集成了数据库,并使用 Spring Data JPA 实现了基本的 CRUD API。我们的应用现在能“记忆”数据了!但是,如果你仔细审视那些 API,会发现它们还很“粗糙”:有…...

NFT模式:数字资产确权与链游经济系统构建
NFT模式:数字资产确权与链游经济系统构建 ——从技术架构到可持续生态的范式革命 一、确权技术革新:构建可信数字资产基石 1. 区块链底层架构的进化 跨链互操作协议:基于LayerZero协议实现以太坊、Solana等公链资产互通,通过零知…...

网络编程(UDP编程)
思维导图 UDP基础编程(单播) 1.流程图 服务器:短信的接收方 创建套接字 (socket)-----------------------------------------》有手机指定网络信息-----------------------------------------------》有号码绑定套接字 (bind)--------------…...

【Oracle】分区表
个人主页:Guiat 归属专栏:Oracle 文章目录 1. 分区表基础概述1.1 分区表的概念与优势1.2 分区类型概览1.3 分区表的工作原理 2. 范围分区 (RANGE Partitioning)2.1 基础范围分区2.1.1 按日期范围分区2.1.2 按数值范围分区 2.2 间隔分区 (INTERVAL Partit…...

佰力博科技与您探讨热释电测量的几种方法
热释电的测量主要涉及热释电系数的测定,这是表征热释电材料性能的重要参数。热释电系数的测量方法主要包括静态法、动态法和积分电荷法。其中,积分电荷法最为常用,其原理是通过测量在电容器上积累的热释电电荷,从而确定热释电系数…...

AI病理诊断七剑下天山,医疗未来触手可及
一、病理诊断困局:刀尖上的医学艺术 1.1 金标准背后的隐痛 病理诊断被誉为"诊断的诊断",医生需通过显微镜观察组织切片,在细胞迷宫中捕捉癌变信号。某省病理质控报告显示,基层医院误诊率达12%-15%,专家会诊…...

CVPR2025重磅突破:AnomalyAny框架实现单样本生成逼真异常数据,破解视觉检测瓶颈!
本文介绍了一种名为AnomalyAny的创新框架,该方法利用Stable Diffusion的强大生成能力,仅需单个正常样本和文本描述,即可生成逼真且多样化的异常样本,有效解决了视觉异常检测中异常样本稀缺的难题,为工业质检、医疗影像…...
