计算3个点的6种分布在平面上的占比
假设平面的尺寸是6*6,用1+1的方式构造2,在用2+1的方式构造3
| 2 | 2 | 2 | 1 | 2 | 2 |
| 2 | 2 | 2 | 1 | 2 | 2 |
| 2 | 2 | 2 | 1 | 2 | 2 |
| 3 | 3 | 3 | x | 3 | 3 |
| 2 | 2 | 2 | 1 | 2 | 2 |
| 2 | 2 | 2 | 1 | 2 | 2 |
在平面上有一个点x,1+1的操作吧平面分成了3部分2a1,2a2,2a3,3部分的比值是
| 2a1 | 2a2 | 2a3 |
| 5 | 25 | 5 |
| 0.143 | 0.714 | 0.143 |

这意味着随机的向6*6的平面上扔2个石子,有71.4%的概率按照2a2的方式分布。
第二步计算2a1+1
| 3 | 3 | 3 | 2 | 3 | 3 |
| 3 | 3 | 3 | 2 | 3 | 3 |
| 1 | 1 | 1 | x | 1 | 1 |
| 1 | 1 | 1 | x | 1 | 1 |
| 3 | 3 | 3 | 2 | 3 | 3 |
| 3 | 3 | 3 | 2 | 3 | 3 |
2a1+1把空间分成3部分3a1,3a2和3a3,数值是10,4,20,因此有

计算2a2+1
| 5 | 5 | 3 | 3 | 5 | 5 |
| 5 | 5 | 3 | 3 | 5 | 5 |
| 4 | 4 | x | 1 | 4 | 4 |
| 4 | 4 | 1 | x | 4 | 4 |
| 5 | 5 | 3 | 3 | 5 | 5 |
| 5 | 5 | 3 | 3 | 5 | 5 |
2a2+1把空间分成了4部分,3a1,3a3,3a4,3a5。数量是,2,8,8,16,因此有

计算2a3+1
| 4 | 4 | 1 | 1 | 4 | 4 |
| 4 | 4 | 1 | 1 | 4 | 4 |
| 4 | 4 | 1 | 1 | 4 | 4 |
| 6 | 6 | x | x | 6 | 6 |
| 4 | 4 | 1 | 1 | 4 | 4 |
| 4 | 4 | 1 | 1 | 4 | 4 |
2a3+1把空间分成3部分,3a1,3a4,3a6,数量是10,20,4,
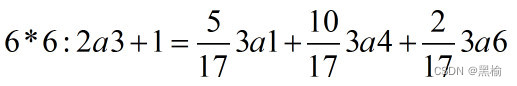
因为2a1:2a2:2a3=1:5:1,因此有

化简

因此在6*6的平面3a1-3a6的占比分别是12.6%,1.68%,25.2%,25.2%,33.6%,1.68%。
这意味着向6*6的格子里随机的扔3个石子,最可能是按照3a5的特征分布,概率是33.6%。出现一行或一竖的概率只有3a5的1/20.
用计算机验证这组数据,随机500次,1000次,2000次
| 500 | % | 1000 | % | 2000 | % | ||||||
| 3a1 | 74 | 0.148 | 120 | 0.12 | 241 | 0.121 | |||||
| 3a2 | 7 | 0.014 | 16 | 0.016 | 22 | 0.011 | |||||
| 3a3 | 106 | 0.212 | 252 | 0.252 | 495 | 0.248 | |||||
| 3a4 | 132 | 0.264 | 261 | 0.261 | 504 | 0.252 | |||||
| 3a5 | 173 | 0.346 | 329 | 0.329 | 707 | 0.354 | |||||
| 3a6 | 8 | 0.016 | 22 | 0.022 | 31 | 0.016 |
数据一致。
相关文章:

计算3个点的6种分布在平面上的占比
假设平面的尺寸是6*6,用11的方式构造2,在用21的方式构造3 2 2 2 1 2 2 2 2 2 1 2 2 2 2 2 1 2 2 3 3 3 x 3 3 2 2 2 1 2 2 2 2 2 1 2 2 在平面上有一个点x,11的操作吧平面分成了3部分2a1,2a…...

【香橙派】实战记录1——简介及烧录 Linux 镜像
文章目录 一、简介1、参数2、结构3、其他配件4、下载资料 二、基于 Windows PC 将 Linux 镜像烧写到 TF 卡的方法1、使用 balenaEtcher 烧录 Linux 镜像的方法2、效果 一、简介 Orange Pi Zero 3 香橙派是一款开源的单板卡片电脑, 新一代的arm64开发板,…...

redis之高可用
(一)redis之高可用 1、在集群当中有一个非常重要的指标,提供正常服务的时间的百分比(365天)99.9% 2、redis的高可用的含义更加广泛,正常服务是指标之一,数据容量的扩展、数据的安全性 3、在r…...

使用 Core Tools 在本地开发 Azure Functions
学习模块 使用 Core Tools 在本地创建和运行 Azure Functions - Training | Microsoft Learn 文档 使用 Core Tools 在本地开发 Azure Functions | Microsoft Learn GitHub - Azure/azure-functions-core-tools: Command line tools for Azure Functions 其它 安装适用于 A…...
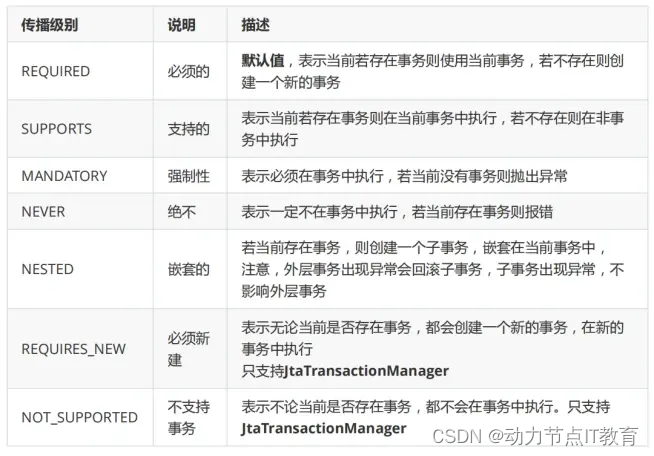
Java零基础——Spring篇
1.Spring框架的介绍 1.1 传统的项目的架构 在传统的项目中,一般遵循MVC开发模型。 (1) view层与用户进行交互,显示数据或者将数据传输给view层。 (2) 在controller层创建service层对象,调用service层中业务方法。 (3) 在service层创建dao…...
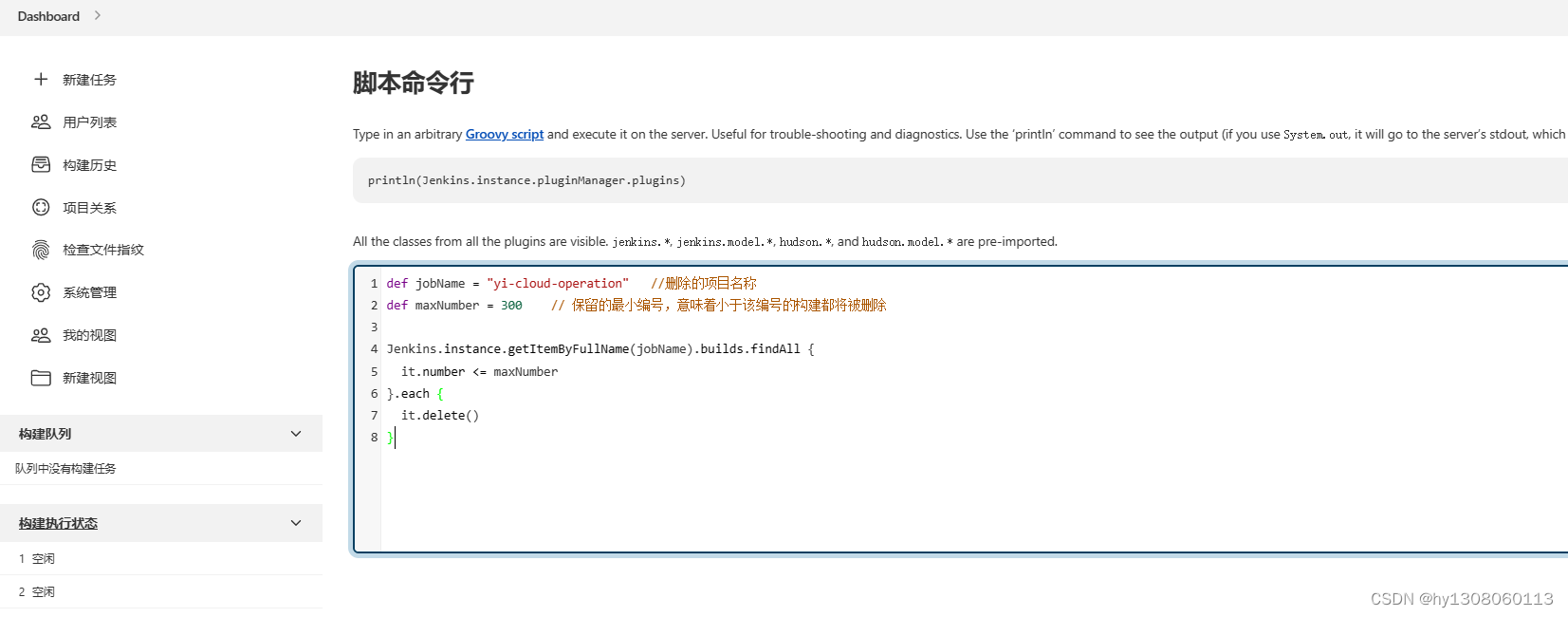
jenkins清理缓存命令
def jobName "yi-cloud-operation" //删除的项目名称 def maxNumber 300 // 保留的最小编号,意味着小于该编号的构建都将被删除 Jenkins.instance.getItemByFullName(jobName).builds.findAll { it.number < maxNumber }.each { it.delet…...

什么是深度学习
一、深度学习的发展历程 1.1 Turing Testing (图灵测试) 图灵测试是人工智能是否真正能够成功的一个标准,“计算机科学之父”、“人工智能之父”英国数学家图灵在1950年的论文《机器会思考吗》中提出了图灵测试的概念。即把一个人和一台计算机分别放在两个隔离的房…...
数字IC基础:有符号数和无符号数加、减法的Verilog设计
相关阅读 数字IC基础https://blog.csdn.net/weixin_45791458/category_12365795.html?spm1001.2014.3001.5482 本文是对数字IC基础:有符号数和无符号数的加减运算一文中的谈到的有符号数加减法的算法进行Verilog实现,有关算法细节请阅读原文࿰…...

2023年11月25日(星期六)骑行三家村
2023年11月25日 (星期六) 骑行三家村(赏红杉林),早8:30到9:00, 大观公园门囗集合,9:30准时出发 【因迟到者,骑行速度快者,可自行追赶偶遇。】 偶遇地点:大观公园门口集合 ,家住东,南…...

.skip() 和 .only() 的使用
.skip() 和 .only() 的使用 说明 在做自动化测试中,跳过执行某些测试用例,或只运行某些指定的测试用例,这种情况是很常见的Cypress中也提供了这种功能 如何跳过测试用例 通过describe.skip() 或者 context.skip() 来跳过不需要执行的测试…...

如何证明特征值的几何重数不超过代数重数
设 λ 0 \lambda_0 λ0 是 A A A 的特征值,则 λ 0 \lambda_0 λ0 的代数重数 ≥ \geq ≥ 几何重数 证明 假设 A A A 的特征值 λ 0 \lambda_0 λ0 对应的特征向量有 q 维,记为 α 1 , . . . , α q \alpha_1, ... , \alpha_q α1,...,…...

Android修行手册-POI操作Excel文档
Unity3D特效百例案例项目实战源码Android-Unity实战问题汇总游戏脚本-辅助自动化Android控件全解手册再战Android系列Scratch编程案例软考全系列Unity3D学习专栏蓝桥系列ChatGPT和AIGC 👉关于作者 专注于Android/Unity和各种游戏开发技巧,以及各种资源分…...

浅析教学型数控车床使用案例
教学型数控车床是一种专为教学和培训设计的机床,它具有小型化、高精度和灵活性的特点,可以作为学校和技术学院的培训机器。下面是一个使用案例,以展示教学型数控车床在教学实训中的应用。 案例背景: 某职业技术学院的机械工程专业…...

图论 2023.11.20
次短路 P2829 大逃离 题意:给定一个无向图,入口1,出口n,求第二短路的值 一个节点所直接连接的地方小于k个(起点和终点除外),那么他就不敢进去。 n<5000,m<100000 思路:次短路…...
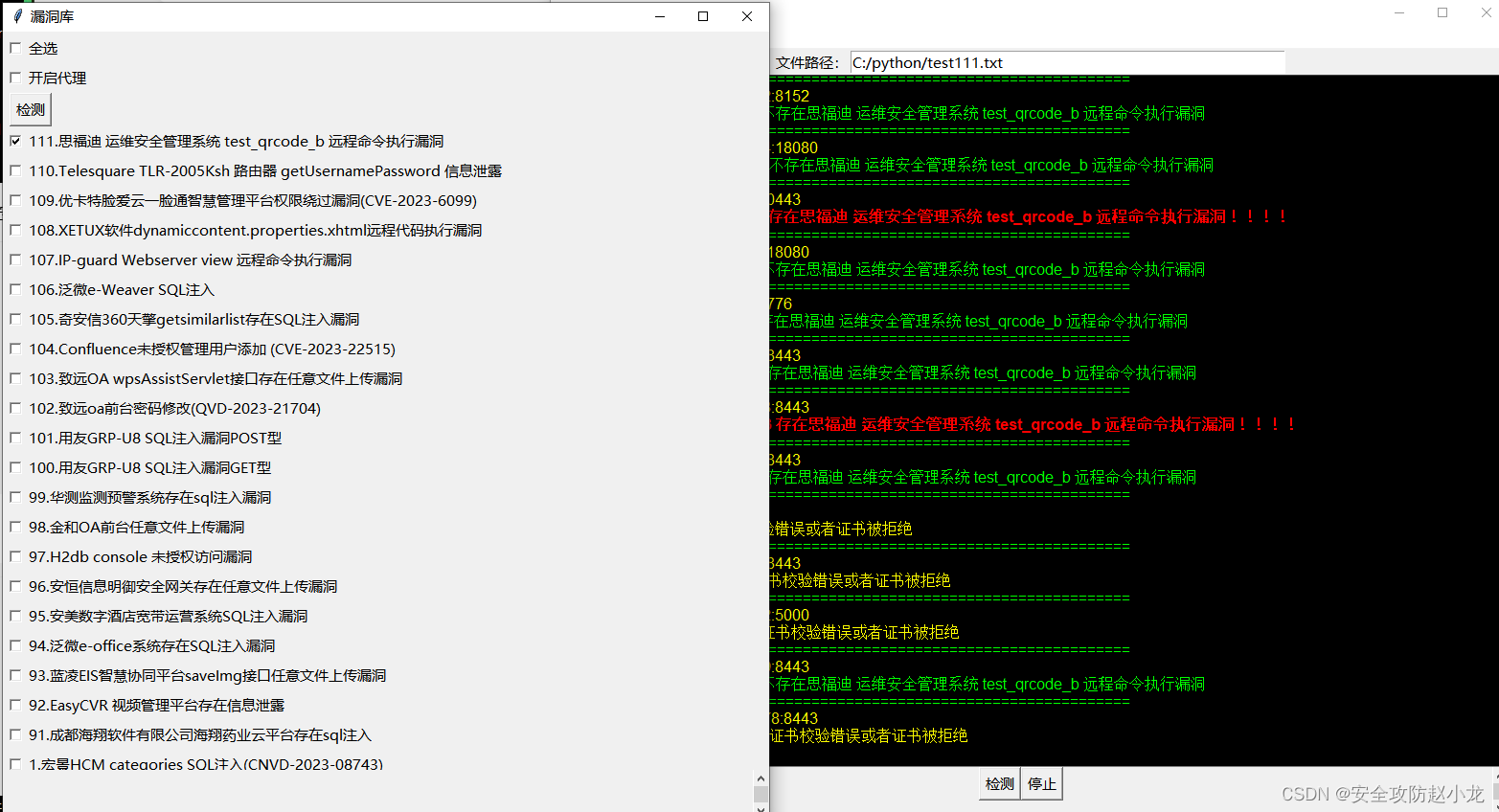
思福迪 运维安全管理系统 test_qrcode_b 远程命令执行漏洞
思福迪 运维安全管理系统 test_qrcode_b 远程命令执行漏洞 一、漏洞描述二、漏洞影响三、网络测绘四、漏洞复现1.手动复现2.自动化复现3.python源代码 免责声明:请勿利用文章内的相关技术从事非法测试,由于传播、利用此文所提供的信息或者工具而造成的任…...

electron项目开机自启动
一、效果展示:界面控制是否需要开机自启动 二、代码实现: 1、在渲染进程login.html中,画好界面,默认勾选; <div class"intro">开机自启动 <input type"checkbox" id"checkbox&quo…...

2023年约特干故城夜间演艺《万方乐奏有于阗》完美谢幕
11月19日,记者走进约特干故城看到演员在欢乐地跳着刀郎舞和古典舞,庆祝今年以来夜间演艺《万方乐奏有于阗》演出200场完美谢幕。 11月19日在约特干故城,演员正在表演迎宾乐舞。阿卜力克木依卜拉依木摄 当天晚上,城楼上旌旗猎猎&am…...
学习网络编程No.10【深入学习HTTPS】
引言: 北京时间:2023/11/14/18:45,因为种种原因,上个月的文章昨天才更新,目前处于刷题前夕,算法课在看了。这次和以前不一样,因为以前对知识框架没有很好的理念,并不清楚相关知识要…...
ubuntu下docker环境使用GPU配置
本文主要讲述整个命令流程,具体讲解请看官网nvidia-容器工具包和一篇总结得很详细的博文docker使用GPU总结 docker的版本必须安装19.0版本以上的,这里也只讲19.0版本以上的使用方法 首先设置一下网络信息 curl -fsSL https://nvidia.github.io/libnvi…...

渗透工具---BurpSuite 插件开发之HelloWorld
本文主要记录如何利用burp官方的新版API即MontoyaApi 写helloworld(上一篇的demo使用旧版api写的,这篇及后续开发将采用新版api) 先看效果图 更多详细内容见下方 这里有更详细更全面的代码内容 以及配置相关的内容 https://mp.weixin.qq.co…...

【Axure高保真原型】引导弹窗
今天和大家中分享引导弹窗的原型模板,载入页面后,会显示引导弹窗,适用于引导用户使用页面,点击完成后,会显示下一个引导弹窗,直至最后一个引导弹窗完成后进入首页。具体效果可以点击下方视频观看或打开下方…...

Linux链表操作全解析
Linux C语言链表深度解析与实战技巧 一、链表基础概念与内核链表优势1.1 为什么使用链表?1.2 Linux 内核链表与用户态链表的区别 二、内核链表结构与宏解析常用宏/函数 三、内核链表的优点四、用户态链表示例五、双向循环链表在内核中的实现优势5.1 插入效率5.2 安全…...

工业安全零事故的智能守护者:一体化AI智能安防平台
前言: 通过AI视觉技术,为船厂提供全面的安全监控解决方案,涵盖交通违规检测、起重机轨道安全、非法入侵检测、盗窃防范、安全规范执行监控等多个方面,能够实现对应负责人反馈机制,并最终实现数据的统计报表。提升船厂…...

2.Vue编写一个app
1.src中重要的组成 1.1main.ts // 引入createApp用于创建应用 import { createApp } from "vue"; // 引用App根组件 import App from ./App.vue;createApp(App).mount(#app)1.2 App.vue 其中要写三种标签 <template> <!--html--> </template>…...

Linux-07 ubuntu 的 chrome 启动不了
文章目录 问题原因解决步骤一、卸载旧版chrome二、重新安装chorme三、启动不了,报错如下四、启动不了,解决如下 总结 问题原因 在应用中可以看到chrome,但是打不开(说明:原来的ubuntu系统出问题了,这个是备用的硬盘&a…...

Axios请求超时重发机制
Axios 超时重新请求实现方案 在 Axios 中实现超时重新请求可以通过以下几种方式: 1. 使用拦截器实现自动重试 import axios from axios;// 创建axios实例 const instance axios.create();// 设置超时时间 instance.defaults.timeout 5000;// 最大重试次数 cons…...

如何理解 IP 数据报中的 TTL?
目录 前言理解 前言 面试灵魂一问:说说对 IP 数据报中 TTL 的理解?我们都知道,IP 数据报由首部和数据两部分组成,首部又分为两部分:固定部分和可变部分,共占 20 字节,而即将讨论的 TTL 就位于首…...

打手机检测算法AI智能分析网关V4守护公共/工业/医疗等多场景安全应用
一、方案背景 在现代生产与生活场景中,如工厂高危作业区、医院手术室、公共场景等,人员违规打手机的行为潜藏着巨大风险。传统依靠人工巡查的监管方式,存在效率低、覆盖面不足、判断主观性强等问题,难以满足对人员打手机行为精…...

API网关Kong的鉴权与限流:高并发场景下的核心实践
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 引言 在微服务架构中,API网关承担着流量调度、安全防护和协议转换的核心职责。作为云原生时代的代表性网关,Kong凭借其插件化架构…...

门静脉高压——表现
一、门静脉高压表现 00:01 1. 门静脉构成 00:13 组成结构:由肠系膜上静脉和脾静脉汇合构成,是肝脏血液供应的主要来源。淤血后果:门静脉淤血会同时导致脾静脉和肠系膜上静脉淤血,引发后续系列症状。 2. 脾大和脾功能亢进 00:46 …...
