2023 年 亚太赛 APMCM ABC题 国际大学生数学建模挑战赛 |数学建模完整代码+建模过程全解全析
当大家面临着复杂的数学建模问题时,你是否曾经感到茫然无措?作为2022年美国大学生数学建模比赛的O奖得主,我为大家提供了一套优秀的解题思路,让你轻松应对各种难题。

以五一杯 A题为例子,以下是咱们做的一些想法呀!
问题1:
(1)建立数学模型:
无人机投放模型在这个问题中的作用是建立数学模型来描述无人机投放爆炸物的过程,并且可以通过该模型来优化无人机投放的策略,从而提高命中率和效率。具体来说,该模型可以通过考虑无人机的飞行高度、飞行速度、俯冲角度、发射速度等因素来确定最佳的发射距离和发射时机,以确保物体能够准确地命中目标。此外,该模型还可以考虑外部因素,如风速和风向等,来调整无人机的飞行轨迹和姿态,以提高投放精度和稳定性。
对于本题的模型,有:
其中 ρ 为空气密度,S 为物资横截面积, 为物资的阻力系数, g 为重力加速度,F 为无人机与物资之间的牵引力。
当无人机投放物资时,物资与无人机之间断开连接,牵引力 F取0,上式可以化简为:
其中为重力加速度。
(2)在无人机的飞行高度为 300m,飞行速度为 300km/h,风速为 5m/s,风向与水平面平行的情况下,使用代码解决:
import
math# 定义常量
v0 = 300 # 飞行速度,单位km/h
vw = 5 # 风速,单位m/s
h = 300 # 飞行高度,单位m
r = 0.2 # 球形物资半径,单位m
m = 50 # 球形物资质量,单位kg
g = 9.8 # 重力加速度,单位m/s^2# 计算投放距离
d0 = v0**2/g * math.sin(0*2*math.pi/360) + vw*v0/g * math.cos(0*2*math.pi/360)
d180 = v0**2/g * math.sin(180*2*math.pi/360) + vw*v0/g * math.cos(180*2*math.pi/360)
d90 = v0**2/g * math.sin(90*2*math.pi/360) + vw*v0/g * math.cos(90*2*math.pi/360)# 输出结果
print(f"无人机飞行方向与风向相同时,投放距离为:{d0:.1f}m")
print(f"无人机飞行方向与风向相反时,投放距离为:{d180:.1f}m")
问题2:
假设无人机在水平飞行过程中到达距离目标点的水平距离为 x ,飞行高度为 ℎ ,飞行速度为v ,俯冲角度为 α ,发射速度为 u 。则无人机发射炸弹的轨迹可以分解为水平方向和竖直方向两个分量。
在水平方向上,无人机在 秒到达目标点,发射炸弹的时间为 秒。发射炸弹时无人机的水平速度为vcosα ,炸弹的水平初速度为 ucosα。
在竖直方向上,炸弹自由落体运动,竖直初速度为 usinα ,竖直加速度为g 。设炸弹飞行的时间为 秒,则有:
将 t3 的值代入到水平方向上的运动中,则可以求得无人机与目标点之间的距离 x1 :
假设无人机发射炸弹的距离为 d ,则需要满足 1000≤d≤3000 。为了使无人机在发射炸弹时仍能保持安全的飞行高度,假设无人机的飞行高度为 800m ,则有 ℎ≥300m 。
为了使发射策略可行,需要选择合适的俯冲角度 α 和发射速度u。假设 α 为定值,可以根据上述模型求出发射速度u与发射距离d的关系,并绘制出其图像,如下图所示。
由图像可知,当俯冲角度为 30∘ 时,发射速度最小,约为 426.8m/s ,此时发射距离为d≈1716.2m
问题3:
无人机的飞行稳定性可以用无人机的俯仰角和偏航角的变化率来描述,即:
其中, θ表示俯仰角, 表示偏航角。这个数值越小,说明无人机的飞行越稳定。
无人机的命中精度可以用命中目标的距离来描述,与无人机的飞行稳定性呈反比关系,即:
在实际应用中,可以通过无人机的传感器数据来计算无人机的俯仰角和偏航角的变化率,并根据上述公式来评估无人机的飞行稳定性和命中精度。
import numpy as np
import matplotlib.pyplot as pltdef dynamic_equation(x, u):# 状态方程A = np.array([[1, 0, 0, dt, 0, 0],[0, 1, 0, 0, dt, 0],[0, 0, 1, 0, 0, dt],[0, 0, 0, 1-0.5*rho*Cd*S/m*dt, 0, 0],[0, 0, 0, 0, 1-0.5*rho*Cd*S/m*dt, 0],[0, 0, 0, 0, 0, 1-0.5*rho*Cd*S/m*dt]])# 输入方程B = np.array([[0, 0, 0, 0],[0, 0, 0, 0],[0, 0, 0, 0],[0, 0, 0, -0.5*rho*S*vx0**2/m*dt],[0, 0, 0, -0.5*rho*S*vx0**2/m*dt],[0, 0, 0, -0.5*rho*S*vx0**2/m*dt]])# 状态更新x_new = np.dot(A, x) + np.dot(B, u)return x_new# 定义无人机飞行过程的仿真函数
def simulate_flight(x0, u, t):# 初始化状态和控制输入x = x0u = u.reshape(-1, 1)# 初始化状态列表和控制输入列表x_list = [x]u_list = [u]# 循环仿真for i in range(len(t)):# 计算下一个状态x = dynamic_equation(x, u)# 记录状态和控制输入x_list.append(x)、、模糊处理 完整版看文章下面~u_list.append(u)# 将列表转换为数组x_array = np.array(x_list)u_array = np.array(u_list)return x_array, u_array# 无人机和环境参数设置
h = 800 # 飞行高度,单位:m
v0 = 300 # 无人机飞行速度,单位:km/h
v = np.linspace(300, 400, 101) / 3.6 # 无人机相对地面速度,单位:m/s
vw = np.array([6, 0]) # 风速,单位:m/s
gamma = np.deg2rad(45) # 俯冲角,单位:rad
g = 9.8 # 重力加速度,单位:m/s^2# 计算无人机稳定性
S = 2 * np.pi * (0.5 ** 2) # 球形爆炸物的参考面积
Cd = 0.5 # 球形爆炸物的阻力系数
m = 50 # 球形爆炸物的质量,单位:kg
rho = 1.2 # 空气密度,单位:kg/m^3
K = 0.5 * rho * S * Cd / m # 阻力系数
u = np.sqrt(v ** 2 + (v0 * np.sin(gamma)) ** 2) # 爆炸物相对空气速度
D = K * u ** 2 # 阻力大小
H = h - np.sqrt((h ** 2) / (np.tan(gamma) ** 2 + 1)) # 爆炸物发射高度
t = (H - 300) / (v0 * np.cos(gamma)) # 爆炸物发射时间
x0 = v0 * t # 无人机前进距离
x = x0 + (v + vw[0]) * t # 爆炸物水平位移距离
y = H - (v0 * np.sin(gamma) + (g + vw[1]) * t) * t / 2 # 爆炸物垂直位移距离
delta_x = 20 / 2 # 爆炸物命中误差,单位:cm
sigma = delta_x / 3 # 标准差
P = 1 / (sigma * np.sqrt(2 * np.pi)) * np.exp(-(x - delta_x) ** 2 / (2 * sigma ** 2)) # 命中概率密度函数
hit_rate = np.trapz(P, x) # 命中率# 可视化结果
plt.plot(v, P)
plt.xlabel('Horizontal displacement (m)')
plt.ylabel('Probability density')
plt.title('Hit probability density')
plt.show()print('The hit rate is %.2f%%.' % (hit_rate * 100))
cs数模团队在亚太赛 APMCM前为大家提供了许多资料的内容呀!!
具体可以看看我的下方的名片!里面包含有亚太赛一手资料与分析!
另外在赛中,我们也会陪大家一起解析亚太赛APMCM的一些方向
关注 CS数模 团队,数模不迷路~
相关文章:

2023 年 亚太赛 APMCM ABC题 国际大学生数学建模挑战赛 |数学建模完整代码+建模过程全解全析
当大家面临着复杂的数学建模问题时,你是否曾经感到茫然无措?作为2022年美国大学生数学建模比赛的O奖得主,我为大家提供了一套优秀的解题思路,让你轻松应对各种难题。 以五一杯 A题为例子,以下是咱们做的一些想法呀&am…...
如何用cmd命令快速搭建FTP服务
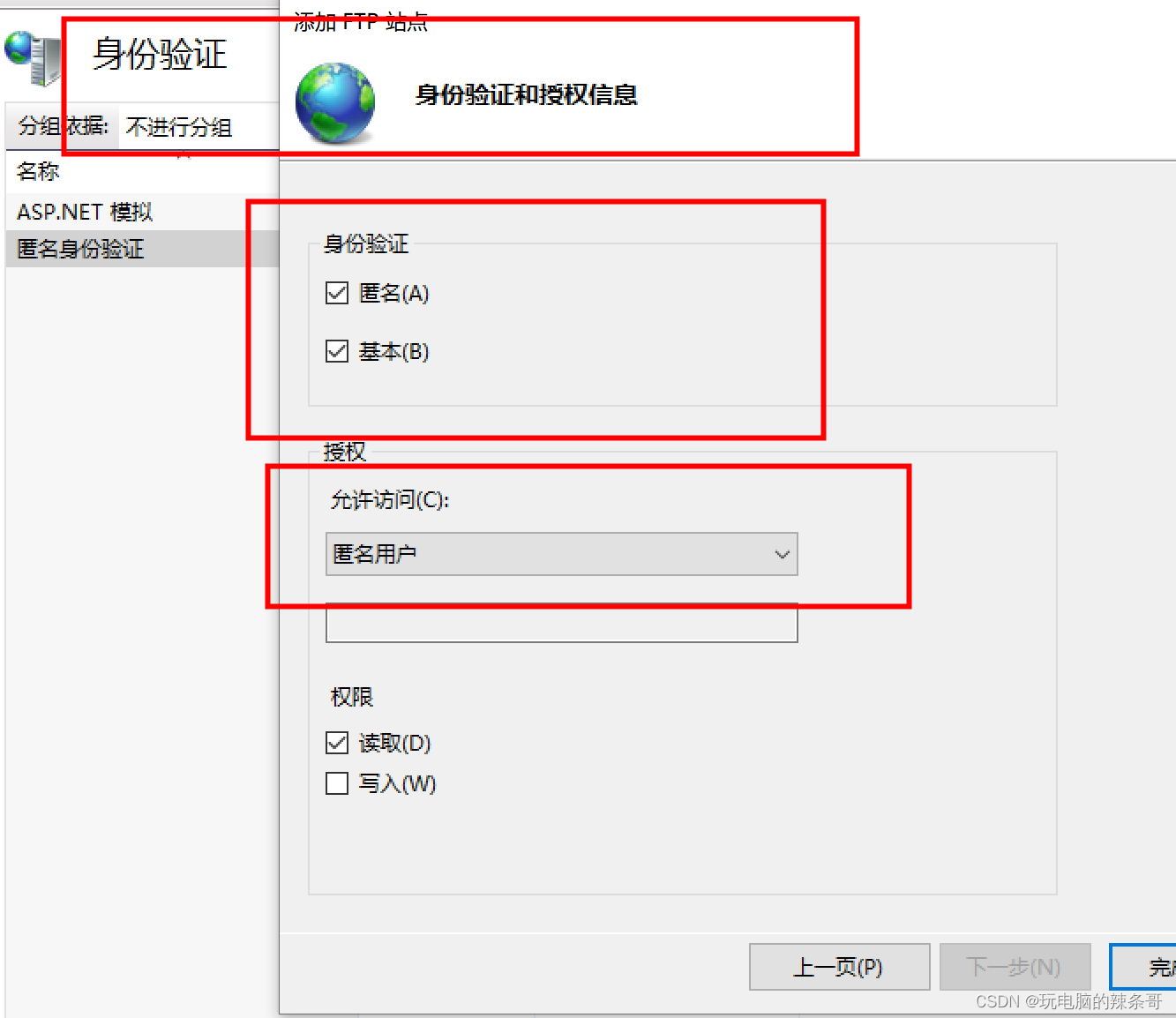
环境: Win10专业版 问题描述: 如何用cmd命令快速搭建FTP服务 解决方案: 1.输入以下命令来安装IIS(Internet Information Services): dism /online /enable-feature /featurename:IIS-FTPServer /all …...
数据结构学习笔记——多维数组、矩阵与广义表
目录 一、多维数组(一)数组的定义(二)二维数组(三)多维数组的存储(四)多维数组的下标的相关计算 二、矩阵(一)特殊矩阵和稀疏矩阵(二)…...
C++之常用的排序算法
C之常用的排序算法 sort #include<iostream> using namespace std; #include<vector> #include<algorithm> #include<functional> void Myptint(int val) {cout << val << " "; }void test() {vector<int> v;v.push_back(…...
Mac中LaTex无法编译的问题
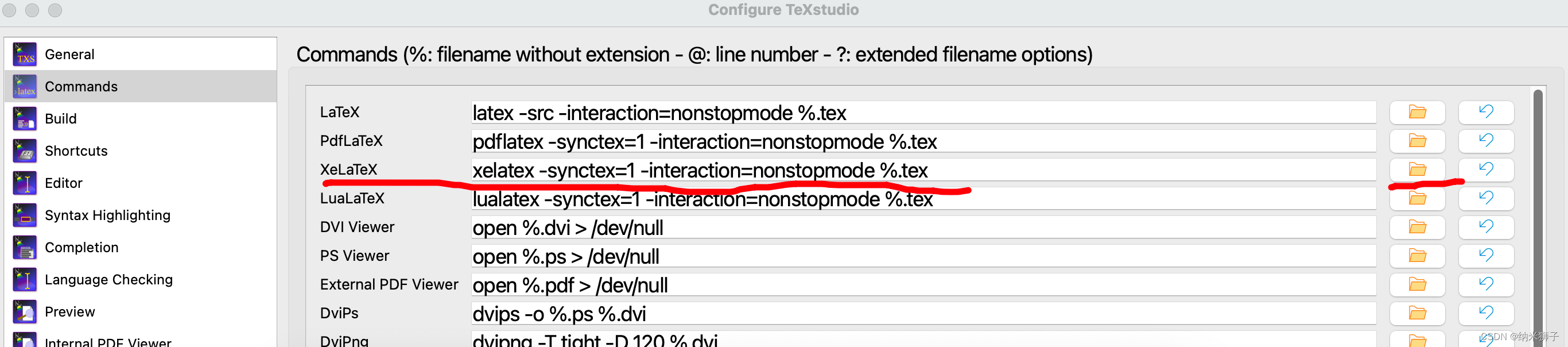
最近在使用TexStudio时,遇到一个棘手的问题: 无法编译,提示如下: kpathsea: Running mktexfmt xelatex.fmt /Library/TeX/texbin/mktexfmt: kpsewhich -var-valueTEXMFROOT failed, aborting early. BEGIN failed–compilation a…...
【Python爬虫】8大模块md文档集合从0到scrapy高手,第7篇:selenium 数据提取详解
本文主要学习一下关于爬虫的相关前置知识和一些理论性的知识,通过本文我们能够知道什么是爬虫,都有那些分类,爬虫能干什么等,同时还会站在爬虫的角度复习一下http协议。 爬虫全套笔记地址: 请移步这里 共 8 章&#x…...

【python基础(三)】操作列表:for循环、正确缩进、切片的使用、元组
文章目录 一. 遍历整个列表1. 在for循环中执行更多操作2. 在for循环结束后执行一些操作 二. 避免缩进错误三. 创建数值列表1. 使用函数range()2. 使用range()创建数字列表3. 指定步长。4. 对数字列表执行简单的统计计算5. 列表解析 五. 使用列表的一部分-切片1. 切片2. 遍历切片…...

使用VSCode调试全志R128的C906 RISC-V核心
使用 VSCode 调试 调试 XuanTie C906 核心 准备工具 T-Head DebugServer(CSkyDebugServer) - 搭建调试服务器 下载地址:T-Head DebugServer手册:T-Head Debugger Server User Guide驱动:cklink_dirvers VSCode - 开…...

Node.js之http模块
http模块是什么? http 模块是 Node,js 官方提供的、用来创建 web 服务器的模块。通过 http 模块提供的 http.createServer() 方法,就能方便的把一台普通的电脑,变成一台Web 服务器,从而对外提供 Web 资源服务。 如果我们想在node…...
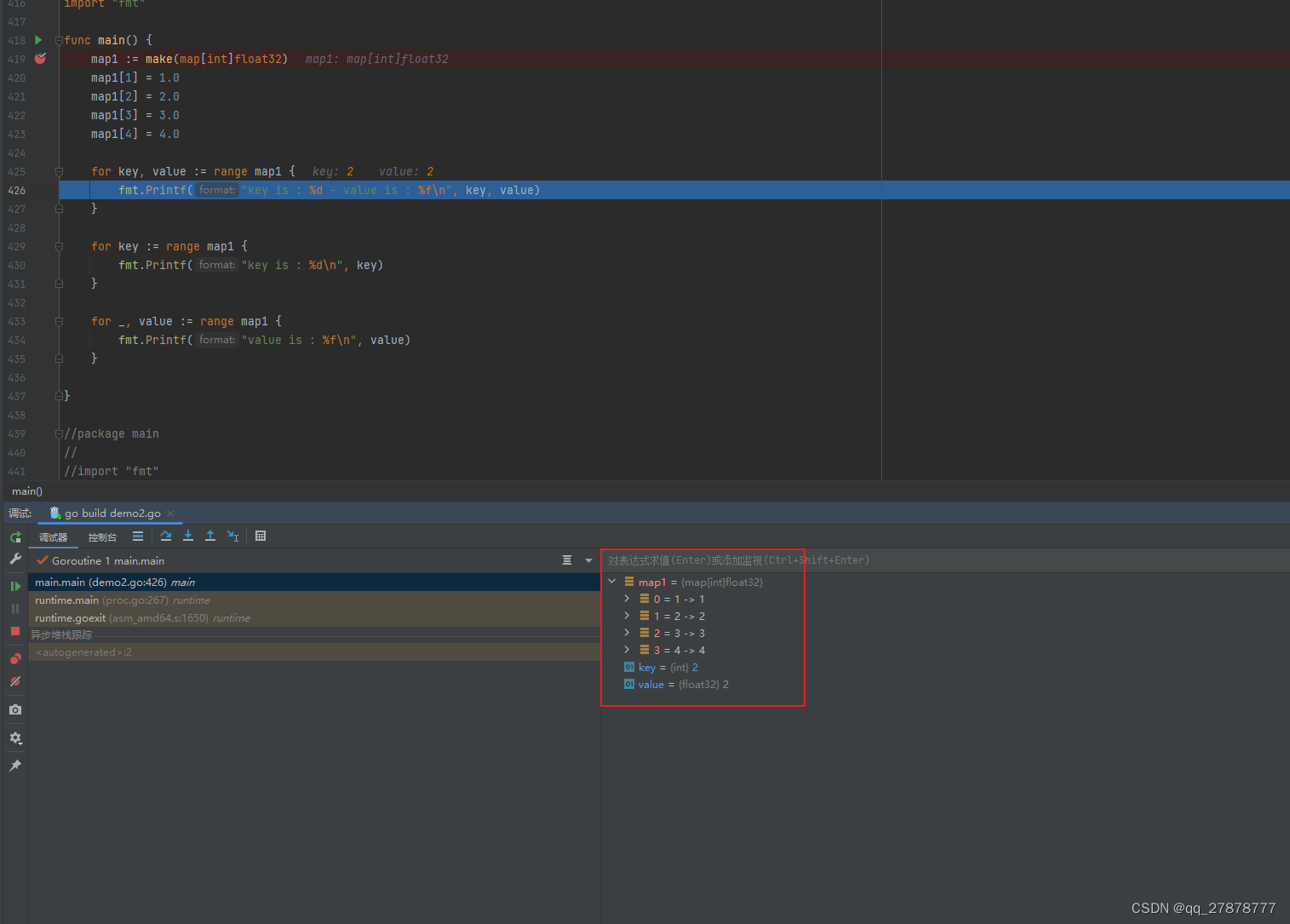
golang 断点调试
1.碰见如下报错,调试器没有打印变量信息 Delve is too old for Go version 1.21.2 (maximum supported version 1.19) 2. 解决办法 升级delve delve是go语言的debug工具。 go install github.com/go-delve/delve/cmd/dlvlatest报错 Get “https://proxy.golang.org/github…...

定时器如何计算触发频率?
定时器触发频率的计算公式为:定时器时钟频率/(预分频系数*计数周期1)。其中,定时器时钟频率是指定时器所连接的总线频率,预分频系数和计数周期需要根据具体的需求进行设置。预分频系数用于将总线频率分频,计…...

【数据库】数据库中的检查点Checkpoint,数据落盘的重要时刻
检查点(checkpoint) 专栏内容: 手写数据库toadb 本专栏主要介绍如何从零开发,开发的步骤,以及开发过程中的涉及的原理,遇到的问题等,让大家能跟上并且可以一起开发,让每个需要的人成为参与者。 本专栏会定…...
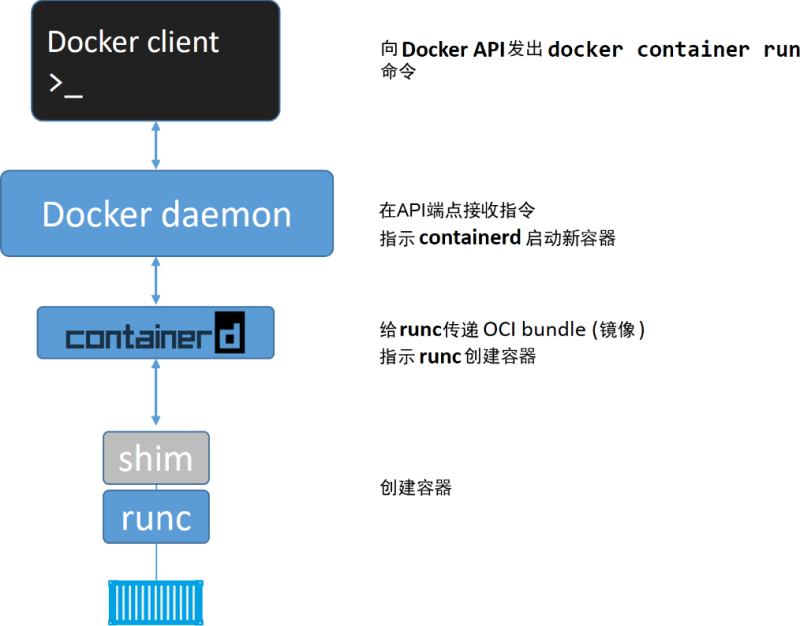
关于 Docker
关于 Docker 1. 术语Docker Enginedockerd(Docker daemon)containerdOCI (Open Container Initiative)runcDocker shimCRI (Container Runtime Interface)CRI-O 2. 容器启动过程在 Linux 中的实现daemon 的作用 Docker 是个划时代的开源项目,…...

LeetCode解法汇总2342. 数位和相等数对的最大和
目录链接: 力扣编程题-解法汇总_分享记录-CSDN博客 GitHub同步刷题项目: https://github.com/September26/java-algorithms 原题链接:力扣(LeetCode)官网 - 全球极客挚爱的技术成长平台 描述: 给你一个下…...

数据库的级联删除
级联删除是指在数据库中删除一个对象时,与该对象有关的其他对象也被自动删除。在 Django 中,级联删除通常通过在模型中定义外键时使用 on_delete 参数来实现。以下是一些常见的 on_delete 选项: 1.models.CASCADE: 当关联的对象被删除时&…...

【Python 千题 —— 基础篇】奇数列表
题目描述 题目描述 创建奇数列表。使用 for 循环创建一个包含 20 以内奇数的列表。 输入描述 无输入。 输出描述 输出创建的列表。 示例 示例 ① 输出: 创建的奇数列表为: [1, 3, 5, 7, 9, 11, 13, 15, 17, 19]代码讲解 下面是本题的代码: #…...

当npm下载库失败时可以用cnpm替代
下载cnpm npm install -g cnpm --registryhttp://registry.npmmirror.com 然后使用cnpm代替npm下载即可 cnpm install...

PyTorch多GPU训练时同步梯度是mean还是sum?
PyTorch 通过两种方式可以进行多GPU训练: DataParallel, DistributedDataParallel. 当使用DataParallel的时候, 梯度的计算结果和在单卡上跑是一样的, 对每个数据计算出来的梯度进行累加. 当使用DistributedDataParallel的时候, 每个卡单独计算梯度, 然后多卡的梯度再进行平均.…...

Spring Framework IoC依赖注入-按Bean类型注入
Spring Framework 作为一个领先的企业级开发框架,以其强大的依赖注入(Dependency Injection,DI)机制而闻名。DI使得开发者可以更加灵活地管理对象之间的关系,而不必过多关注对象的创建和组装。在Spring Framework中&am…...
IDEA运行thymeleaf的html文件打开端口为63342且连不上数据库
这边贴apple.html代码 <!DOCTYPE html> <html xmlns:th"http://www.thymeleaf.org"> <head><meta charset"UTF-8"><title>User List</title> </head> <body> <h1>User List</h1> <table&…...

国防科技大学计算机基础课程笔记02信息编码
1.机内码和国标码 国标码就是我们非常熟悉的这个GB2312,但是因为都是16进制,因此这个了16进制的数据既可以翻译成为这个机器码,也可以翻译成为这个国标码,所以这个时候很容易会出现这个歧义的情况; 因此,我们的这个国…...

【WiFi帧结构】
文章目录 帧结构MAC头部管理帧 帧结构 Wi-Fi的帧分为三部分组成:MAC头部frame bodyFCS,其中MAC是固定格式的,frame body是可变长度。 MAC头部有frame control,duration,address1,address2,addre…...

C/C++ 中附加包含目录、附加库目录与附加依赖项详解
在 C/C 编程的编译和链接过程中,附加包含目录、附加库目录和附加依赖项是三个至关重要的设置,它们相互配合,确保程序能够正确引用外部资源并顺利构建。虽然在学习过程中,这些概念容易让人混淆,但深入理解它们的作用和联…...

PostgreSQL——环境搭建
一、Linux # 安装 PostgreSQL 15 仓库 sudo dnf install -y https://download.postgresql.org/pub/repos/yum/reporpms/EL-$(rpm -E %{rhel})-x86_64/pgdg-redhat-repo-latest.noarch.rpm# 安装之前先确认是否已经存在PostgreSQL rpm -qa | grep postgres# 如果存在࿰…...

嵌入式常见 CPU 架构
架构类型架构厂商芯片厂商典型芯片特点与应用场景PICRISC (8/16 位)MicrochipMicrochipPIC16F877A、PIC18F4550简化指令集,单周期执行;低功耗、CIP 独立外设;用于家电、小电机控制、安防面板等嵌入式场景8051CISC (8 位)Intel(原始…...

麒麟系统使用-进行.NET开发
文章目录 前言一、搭建dotnet环境1.获取相关资源2.配置dotnet 二、使用dotnet三、其他说明总结 前言 麒麟系统的内核是基于linux的,如果需要进行.NET开发,则需要安装特定的应用。由于NET Framework 是仅适用于 Windows 版本的 .NET,所以要进…...

Qt学习及使用_第1部分_认识Qt---Qt开发基本流程
前言 学以致用,通过QT框架的学习,一边实践,一边探索编程的方方面面. 参考书:<Qt 6 C开发指南>(以下称"本书") 标识说明:概念用粗体倾斜.重点内容用(加粗黑体)---重点内容(红字)---重点内容(加粗红字), 本书原话内容用深蓝色标识,比较重要的内容用加粗倾…...

解决MybatisPlus使用Druid1.2.11连接池查询PG数据库报Merge sql error的一种办法
目录 前言 一、问题重现 1、环境说明 2、重现步骤 3、错误信息 二、关于LATERAL 1、Lateral作用场景 2、在四至场景中使用 三、问题解决之道 1、源码追踪 2、关闭sql合并 3、改写处理SQL 四、总结 前言 在博客:【写在创作纪念日】基于SpringBoot和PostG…...
Web APIS Day01
1.声明变量const优先 那为什么一开始前面就不能用const呢,接下来看几个例子: 下面这张为什么可以用const呢?因为复杂数据的引用地址没变,数组还是数组,只是添加了个元素,本质没变,所以可以用con…...

Java + Spring Boot + Mybatis 插入数据后,获取自增 id 的方法
在 MyBatis 中使用 useGeneratedKeys"true" 获取新插入记录的自增 ID 值,可通过以下步骤实现: 1. 配置 Mapper XML 在插入语句的 <insert> 标签中设置: xml 复制 下载 运行 <insert id"insertUser" para…...
