2017年全国硕士研究生入学统一考试管理类专业学位联考数学试题——解析版
文章目录
- 2017 级考研管理类联考数学真题解析
- 一、问题求解(本大题共 5 小题,每小题 3 分,共 45 分)下列每题给出 5 个选项中,只有一个是符合要求的,请在答题卡上将所选择的字母涂黑。
- 真题(2017-01)-应用题-
- 真题(2017-02)-应用题
- 真题(2017-03)-数列-等差数列
- 真题(2017-04)-算术-绝对值
- 真题(2017-05)-几何-平面几何
- 真题(2017-06)-应用题
- 真题(2017-07)-实数-整除
- 真题(2017-08)-概率
- 真题(2017-09)-几何-平面几何
- 真题(2017-10)-应用题-不定方程
- 真题(2017-11)-几何-平面几何-三角形
- 真题(2017-12)-数据分析-
- 真题(2017-13)-几何-立体几何
- 真题(2017-14)-数据分析-方差
- 真题(2017-15)-数据分析-分组分配
- 二.条件充分性判断:(第 16-25 小题,每小题 3 分,共 30 分)
- 真题(2017-16)-D-应用题-工程
- 真题(2017-17)-A-几何-解析几何-圆的方程
- 真题(2017-18)-C-应用题-路程
- 真题(2017-19)-B-几何-解析几何
- 真题(2017-20)-E-比例应用题-增长率
- 真题(2017-21)-B-几何-立体几何
- 真题(2017-22)-A-代数-数列
- 真题(2017-23)-C-概率
- 真题(2017-24)-C-应用题
- 真题(2017-25)-A-实数
2017 级考研管理类联考数学真题解析
一、问题求解(本大题共 5 小题,每小题 3 分,共 45 分)下列每题给出 5 个选项中,只有一个是符合要求的,请在答题卡上将所选择的字母涂黑。
真题(2017-01)-应用题-
1.某品牌电冰箱连续两次降价10% 后的售价是降价前的( )
A. 80%
B. 81%
C. 82%
D. 83%
E. 85%

真题(2017-02)-应用题
2.张老师到一所中学进行招生咨询,上午接到了 45 名同学的咨询,其中的 9 位同学下午又咨询了张老师,占张老师下午咨询学生的 10%,一天中向张老师咨询的学生人数为( )
A.81
B.90
C.115
D.126
E.135

真题(2017-03)-数列-等差数列
3.甲、乙、丙三种货车载重量成等差数列,2 辆甲种车和 1 辆乙种车的满载量为 95 吨,1辆甲种车和 3 辆丙种车载重量为 150 吨,则用甲、乙、丙各一辆车一次最多运送货物为( )吨
A.125
B.120
C.115
D.110
E.105

真题(2017-04)-算术-绝对值
4.不等式 ∣ x − 1 ∣ + x ≤ 2 |x-1|+x≤2 ∣x−1∣+x≤2的解集为( )
A. ( − ∞ , 1 ] (-∞,1] (−∞,1]
B. ( − ∞ , 3 2 ] (-∞,\frac{3}{2}] (−∞,23]
C. [ 1 , 3 2 ] [1,\frac{3}{2}] [1,23]
D. [ 1 , + ∞ ) [1,+∞) [1,+∞)
E. [ 3 2 , + ∞ ) [\frac{3}{2},+∞) [23,+∞)
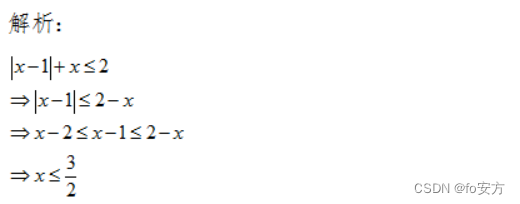
真题(2017-05)-几何-平面几何
5.某种机器人可搜索到的区域是半径为 1 米的圆,若该机器人沿直线行走 10 米,则其搜索出的区域的面积(单位:平方米)为( )
A. 10 + π 2 10+\frac{π}{2} 10+2π
B.10+π
C. 20 + π 2 20+\frac{π}{2} 20+2π
D.20+π
E.10π

真题(2017-06)-应用题
6.老师问班上 50 名同学周末复习情况,结果有 20 人复习过数学、30 人复习过语文、6 人复习过英语,且同时复习过数学和语文的有 10 人、同时复习过语文和英语的有 2 人、同时复习过英语和数学的有 3 人。若同时复习过这三门课的人为 0,则没有复习过这三门课程的学生人数为( )
A.7
B.8
C.9
D.10
E.11

真题(2017-07)-实数-整除
7.在 1 到 100 之间,能被 9 整除的整数的平均值是( )
A.27
B.36
C.45
D.54
E.63

真题(2017-08)-概率
8.某试卷由 15 道选择题组成,每道题有 4 个选项,其中只有一项是符合试题要求的,甲有6 道题能确定正确选项,有 5 道能排除 2 个错误选项,有 4 道能排除 1 个错误选项,若从每题排除后剩余的选项中选一个作为答案,则甲得满分的概率为( )
A. 1 2 4 × 1 3 5 \frac{1}{2^4}×\frac{1}{3^5} 241×351
B. 1 2 5 × 1 3 4 \frac{1}{2^5}×\frac{1}{3^4} 251×341
C. 1 2 5 × 1 3 4 \frac{1}{2^5}×\frac{1}{3^4} 251×341
D. 1 2 4 × ( 3 4 ) 5 \frac{1}{2^4}×(\frac{3}{4})^5 241×(43)5
E. 1 2 4 × ( 3 4 ) 5 \frac{1}{2^4}×(\frac{3}{4})^5 241×(43)5

真题(2017-09)-几何-平面几何
9.如图,在扇形 AOB 中, ∠ A O B = π 4 , O A = 1 , ∠AOB=\frac{π}{4},OA=1, ∠AOB=4π,OA=1, AC 垂直于OB,则阴影部分的面积为( )
A. π 8 − 1 4 \frac{π}{8}-\frac{1}{4} 8π−41
B. π 8 − 1 8 \frac{π}{8}-\frac{1}{8} 8π−81
C. π 4 − 1 2 \frac{π}{4}-\frac{1}{2} 4π−21
D. π 4 − 1 4 \frac{π}{4}-\frac{1}{4} 4π−41
E. π 4 − 1 8 \frac{π}{4}-\frac{1}{8} 4π−81
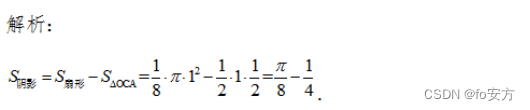
真题(2017-10)-应用题-不定方程
10.某公司用 1 万元购买了价格分别为 1750 和 950 元的甲、乙两种办公设备,则购买的甲、乙办公设备的件数分别为( )
A.3,5
B.5,3
C.4,4
D.2,6
E.6,2

真题(2017-11)-几何-平面几何-三角形
11.已知△ABC 和△A’ B’C’ 满足 ∣ A B ∣ : ∣ A 1 B 1 ∣ = ∣ A C ∣ : ∣ A C 1 ∣ = 2 : 3 , ∠ A + ∠ A 1 = π |AB|:|A^1B^1|=|AC|:|AC^1|=2:3,∠A+∠A^1=π ∣AB∣:∣A1B1∣=∣AC∣:∣AC1∣=2:3,∠A+∠A1=π,则△ABC和△ A 1 B 1 C 1 A^1B^1C^1 A1B1C1的面积比为( )
A. 2 : 3 \sqrt{2}:\sqrt{3} 2:3
B. 3 : 5 \sqrt{3}:\sqrt{5} 3:5
C.2:3
D.2:5
E.4:9
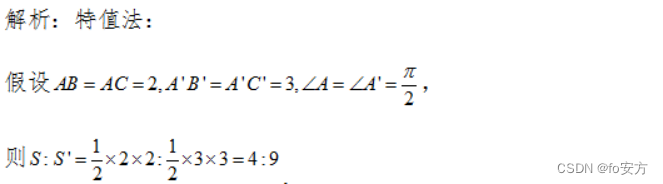
真题(2017-12)-数据分析-
12.甲从 1、2、3 中抽取一个数,记为a ;乙从 1、2、3、4 中抽取一个数,记为b ,规定当a > b 或者a + 1 < b 时甲获胜,则甲取胜的概率为( )
A. 1 6 \frac{1}{6} 61
B. 1 4 \frac{1}{4} 41
C. 1 3 \frac{1}{3} 31
D. 5 12 \frac{5}{12} 125
E. 1 2 \frac{1}{2} 21

真题(2017-13)-几何-立体几何
13.将长、宽、高分别为 12、9 和 6 的长方体切割成正方体,且切割后无剩余,则能切割成相同正方体的最少个数为( )个
A.3
B.6
C.24
D.96
E.648

真题(2017-14)-数据分析-方差
14.甲、乙、丙三人每轮各投篮 10 次,投了三轮.投中数如下表:
| 第一轮 | 第二轮 | 第三轮 | |
|---|---|---|---|
| 甲 | 2 | 5 | 8 |
| 乙 | 5 | 2 | 5 |
| 丙 | 8 | 4 | 9 |
记σ1 ,σ2 ,σ3 分别为甲、乙、丙投中数的方差,则( )
A.σ1>σ2>σ3
B.σ1>σ3>σ2
C.σ2>σ1>σ3
D.σ2>σ3>σ1
E.σ3>σ2>σ1

真题(2017-15)-数据分析-分组分配
15.将 6 人分成 3 组,每组 2 人,则不同的分组方式共有( )种
A.12
B.15
C.30
D.45
E.90

二.条件充分性判断:(第 16-25 小题,每小题 3 分,共 30 分)
要求判断每题给出的条件(1)和(2)能否充分支持题干所陈述的结论,A、B、C、D、E 五个选项为判断结果,请选择一项符合试题要求的判断,请在答题卡上将所选的字母涂黑。
(A)条件(1)充分,但条件(2)不充分
(B)条件(2)充分,但条件(1)不充分
(C)条件(1)和(2)都不充分,但联合起来充分
(D)条件(1)充分,条件(2)也充分
(E)条件(1)不充分,条件(2)也不充分,联合起来仍不充分
真题(2017-16)-D-应用题-工程
16.某人需要处理若干份文件,第一个小时处理了全部文件的 15,第二个小时处理了剩余文件的 14,则此人需要处理的文件共 25 份。
(1)前两小时处理了 10 份文件
(2)第二小时处理了 5 份文件

真题(2017-17)-A-几何-解析几何-圆的方程
17.圆 x 2 + y 2 − a x − b y + c = 0 x^2+y^2-ax-by+c=0 x2+y2−ax−by+c=0与 x 轴相切,则能确定c 的值。
(1)已知a 的值
(2)已知b 的值
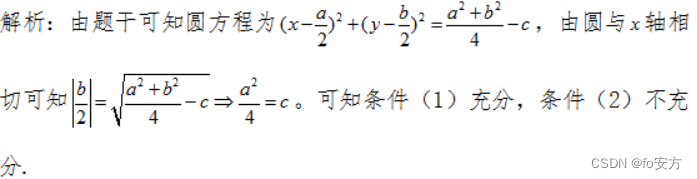
真题(2017-18)-C-应用题-路程
18.某人从 A 地出发,先乘时速为 220 千米的动车,后转乘时速为 100 千米的汽车到达 B 地,则 A,B 两地的距离为 960 千米。
(1)乘动车的时间与乘汽车的时间相等
(2)乘动车的时间与乘汽车的时间之和为 6 小时

真题(2017-19)-B-几何-解析几何
19.直线 y = a x + b y=ax+b y=ax+b与抛物线 y = x 2 y=x^2 y=x2 有两个交点.
(1) a 2 > 4 b a^2>4b a2>4b
(2) b >0

真题(2017-20)-E-比例应用题-增长率
20.能确定某企业产值的月平均增长率
(1)已知一月份的产值
(2)已知全年的总产值答案

答案应该是E。(否则2017年没有选E)
首先理解“月平均增长率x”:只与第一个月和最后一个月的产值有关。如:一月a、二、三、四…十一、十二月3a: a ( 1 + x ) 11 = 3 a a(1+x)^{11}=3a a(1+x)11=3a,得 ( 1 + x ) 11 = 3 (1+x)^{11}=3 (1+x)11=3,得: x = 3 11 − 1 x=\sqrt[11]{3}-1 x=113−1
∴(2)全年总产值是无关的。更改为“12月的产值”,才选C。
真题(2017-21)-B-几何-立体几何
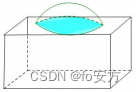
21.如图,一个铁球沉入水池中,则能确定铁球的体积。
(1)已知铁球露出水面的高度
(2)已知水深及铁球与水面交线的周长

真题(2017-22)-A-代数-数列
22.设a, b 是两个不相等的实数,则函数 f ( x ) = x 2 + 2 a x + b f(x)=x^2+2ax+b f(x)=x2+2ax+b 的最小值小于零。
(1)1, a, b 成等差数列
(2)1, a, b 成等比数列

真题(2017-23)-C-概率
23.某人参加资格考试,有 A 类和 B 类选择,A 类的合格标准是抽 3 道题至少会做 2 道,B 类的合格标准是抽 2 道题须都会做,则此人参加 A 类合格的机会大。
(1)此人 A 类题中有 60%会做
(2)此人 B 类题中有 80%会做

真题(2017-24)-C-应用题
24.某机构向 12 位教师征题,共征集到 5 种题型的试题 52 道,则能确定供题教师的人数。
(1)每位供题教师提供题数相同
(2)每位供题教师提供的题型不超过 2 种

真题(2017-25)-A-实数
25.已知a, b, c 为三个实数,则min{ ∣ a − b ∣ , ∣ b − c ∣ , ∣ a − c ∣ |a-b|,|b-c|,|a-c| ∣a−b∣,∣b−c∣,∣a−c∣} ≤ 5 .
(1) ∣ a ∣ ≤ 5 , ∣ b ∣ ≤ 5 , ∣ c ∣ ≤ 5 |a|≤5,|b|≤5,|c|≤5 ∣a∣≤5,∣b∣≤5,∣c∣≤5
(2) a + b + c = 15 a + b + c = 15 a+b+c=15


相关文章:

2017年全国硕士研究生入学统一考试管理类专业学位联考数学试题——解析版
文章目录 2017 级考研管理类联考数学真题解析一、问题求解(本大题共 5 小题,每小题 3 分,共 45 分)下列每题给出 5 个选项中,只有一个是符合要求的,请在答题卡上将所选择的字母涂黑。真题(2017-…...

2、基础入门——web应用架构搭建漏洞HTTP数据包代理服务器
Web应用环境架构类 开发语言:php、java、python、ASP、ASPX等程序源码:用的人多了,就成CMS了。中间件容器:IIS、Apache、Nginx、Tomcat、Weblogic、Jboos、glasshfish等数据库类型:Access、Mysql、Mssql、Oracle、Red…...

【精选】OpenCV多视角摄像头融合的目标检测系统:全面部署指南&源代码
1.研究背景与意义 随着计算机视觉和图像处理技术的快速发展,人们对于多摄像头拼接行人检测系统的需求日益增加。这种系统可以利用多个摄像头的视角,实时监测和跟踪行人的活动,为公共安全、交通管理、视频监控等领域提供重要的支持和帮助。 …...

力扣算法练习BM45—滑块窗口的最大值
题目 给定一个长度为 n 的数组 num 和滑动窗口的大小 size ,找出所有滑动窗口里数值的最大值。 例如,如果输入数组{2,3,4,2,6,2,5,1}及滑动窗口的大小3,那么一共存在6个滑动窗口,他们的最大值分别为{4,4,6,6,6,5}; 针…...

最小二乘估计及与极大似然估计的关系
最小二乘估计(Least Squares Estimation)和极大似然估计(Maximum Likelihood Estimation)是统计学中常用的参数估计方法,它们在某些情况下是等价的,但在一般情况下并不总是相同的。 最小二乘估计ÿ…...
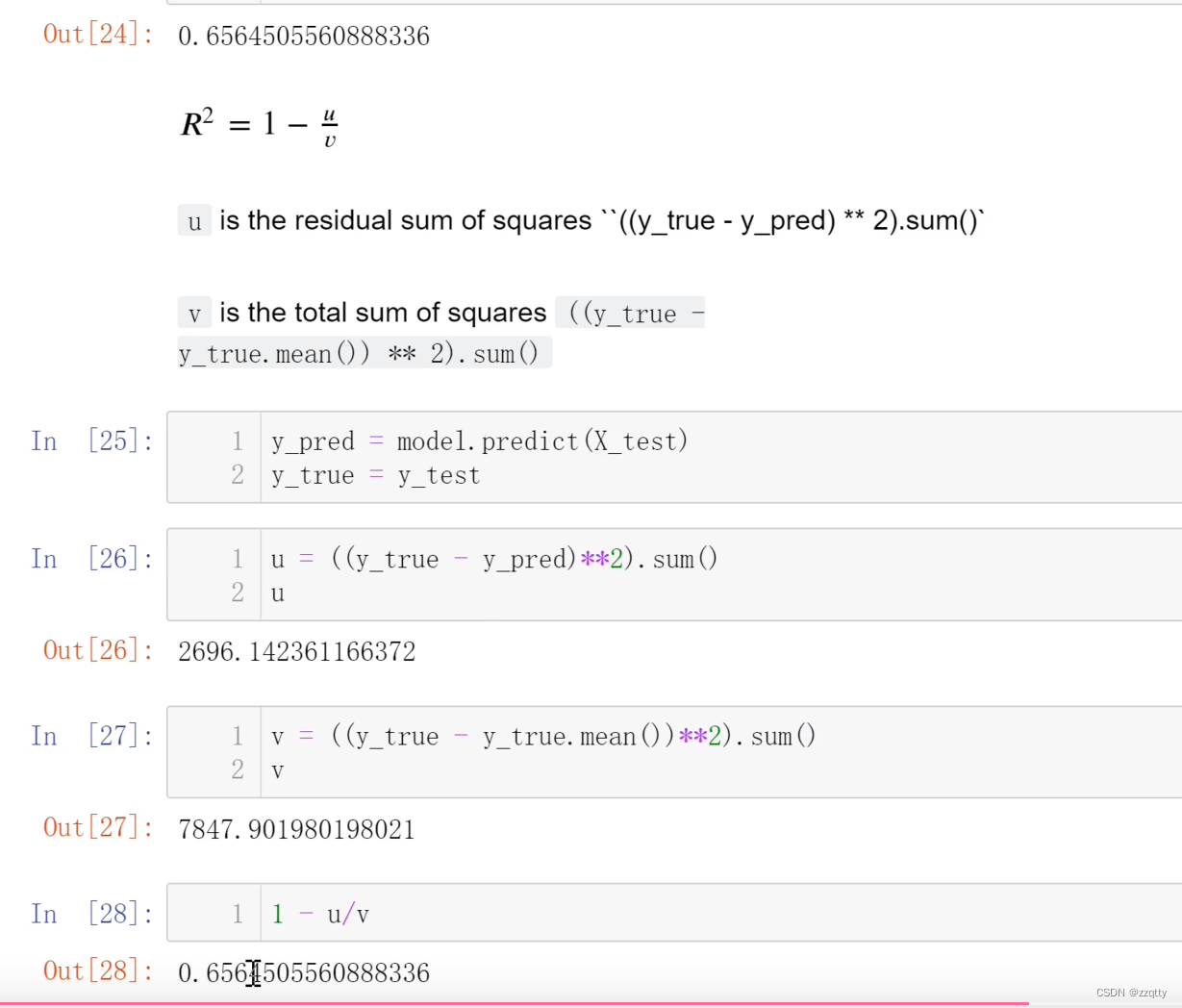
02房价预测
目录 代码 评分算法: 代码 import numpy as np from sklearn import datasets from sklearn.linear_model import LinearRegression# 指定版本才有数据集 # C:\Users\14817\PycharmProjects\pythonProject1\venv\Scripts\activate.bat # pip install scikit-le…...

【Springboot】pom.xml中的<build>标签详解
默认值及其标签解释 <build><!-- 指定最终构建产物的名称, 例如生成的 JAR 文件的名称 --><finalName>${artifactId}-${version}</finalName><!-- 指定源代码文件的目录路径 --><sourceDirectory>src/main/java</sourceDirectory>&l…...
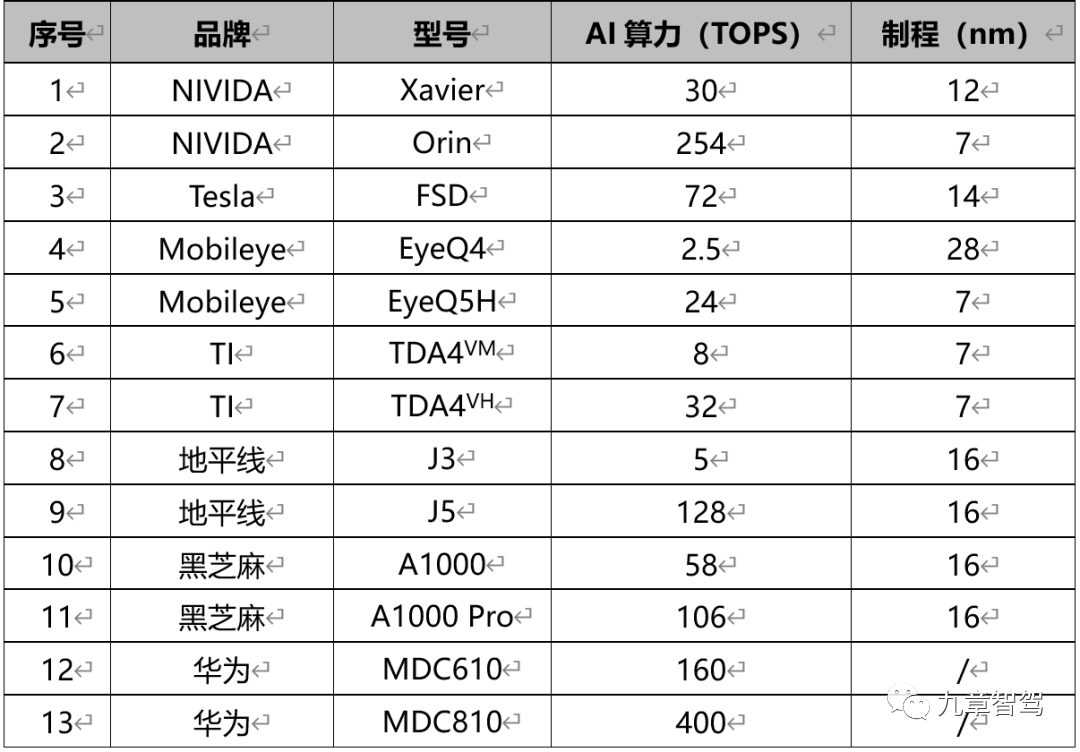
智能驾驶产品开发中如何贯彻“正向开发”理念
摘要: 基于演绎法的正向开发理念,能够让智能驾驶产品在充分满足用户需求,保证产品质量的同时,确保开发目标合理且得到落实。 前段时间,微博CEO吐槽理想L9智能驾驶“行驶轨迹不居中”,在网上引发了热烈讨论…...
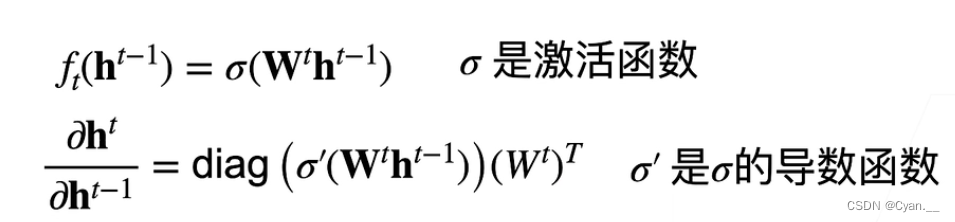
【机器学习】038_梯度消失、梯度爆炸
一、原因 神经网络梯度 假设现在有一个 层的神经网络,每层的输出为一个对输入作 变换的函数结果 用 来表示第 层的输出,那么有下列公式: 链式法则计算损失 关于某一层某个参数 的梯度: 注意到, 为向量&am…...
【转】OAK-D双目相机进行标定及标定结果说明
编辑:OAK中国 首发:A. hyhCSDN 喜欢的话,请多多👍⭐️✍ 内容来自用户的分享,如有疑问请与原作者交流! ▌前言 Hello,大家好,这里是OAK中国,我是助手君。 近期在CSDN刷…...

whip和whep
原文为runner365.git大佬的文章 原文链接:https://blog.csdn.net/sweibd/article/details/124552793 WHIP接口 什么是whip 全称: WebRTC-HTTP ingestion protocol (WHIP). rfc地址: rfc-draft-murillo-whip-00 简单说,就是通过HTTP接口能导入webrtc媒…...

SpringBoot集成jjwt和使用
1.引入jwt依赖(这里以jjwt为例,具体其他jwt产品可以参见jwt官网) <dependency><groupId>io.jsonwebtoken</groupId><artifactId>jjwt</artifactId><version>0.9.1</version> </dependency>…...

RedisConnectionFactory is required已解决!!!!
1.起因🤶🤶🤶🤶 redis搭建完成后,准备启动主程序,异常兴奋,结果报错了!!!! 2.究竟是何原因 😭😭😭…...

redis的高可用之持久化
1、redis的高可用考虑指标 (1)正常服务 (2)数据容量的扩展 (3)数据的安全性 2、redis实现高可用的四种方式 (1)持久化 (2)主从复制 (3&…...
onnx模型转换opset版本和固定动态输入尺寸
背景:之前我想把onnx模型从opset12变成opset12,太慌乱就没找着,最近找到了官网上有示例的,大爱onnx官网,分享给有需求没找着的小伙伴们。 1. onnx模型转换opset版本 官网示例: import onnx from onnx im…...
远程运维如何更高效的远程管理?向日葵的这几项功能会帮到你
远程运维如何更高效的远程管理?向日葵的这几项功能会帮到你 具备一定规模的企业,其IT运维需求普遍会面临设备数量众多、难以统一高效管理、始终存在安全敞口等问题,尤其是针对分部广泛的无人值守设备时,更是如此。 举一个简单的例…...

python BDD 的相关概念
在Python 语言中进行BDD的规格和测试文件的编写的时候,常常会遇到下面的概念: Fixture : 测试设施。设定测试环境的预设状态或值的机制。Background: 背景。所有场景的公共部分。Scenario: 场景。Given : 前置条件Whe…...

【Exception】Error: Dynamic require of “path“ is not supported
Talk is cheap, show me the code. 环境 | Environment kversionOSwindows 11Node.jsv18.14.2npm9.5.0vite5.0.0vue3.3.8 报错日志 | Error log >npm run dev> app10.0.0 dev > viteERROR failed to load config from C:\code\frontend\app1\vite.config.js …...

【蓝桥杯选拔赛真题25】C++两个数比大小 第十三届蓝桥杯青少年创意编程大赛C++编程选拔赛真题解析
目录 C/C++两个数比大小 一、题目要求 1、编程实现 2、输入输出 二、算法分析...
)
C++学习——C++运算符重载(含义、格式、示例、遵循的规则)
以下内容源于C语言中文网的学习与整理,非原创,如有侵权请告知删除。 一、运算符重载的含义 所谓重载,就是赋予新的含义。函数重载(Function Overloading)可以让一个函数名有多种功能,在不同情况下进行不同…...

阿里云ACP云计算备考笔记 (5)——弹性伸缩
目录 第一章 概述 第二章 弹性伸缩简介 1、弹性伸缩 2、垂直伸缩 3、优势 4、应用场景 ① 无规律的业务量波动 ② 有规律的业务量波动 ③ 无明显业务量波动 ④ 混合型业务 ⑤ 消息通知 ⑥ 生命周期挂钩 ⑦ 自定义方式 ⑧ 滚的升级 5、使用限制 第三章 主要定义 …...

Vue3 + Element Plus + TypeScript中el-transfer穿梭框组件使用详解及示例
使用详解 Element Plus 的 el-transfer 组件是一个强大的穿梭框组件,常用于在两个集合之间进行数据转移,如权限分配、数据选择等场景。下面我将详细介绍其用法并提供一个完整示例。 核心特性与用法 基本属性 v-model:绑定右侧列表的值&…...

对WWDC 2025 Keynote 内容的预测
借助我们以往对苹果公司发展路径的深入研究经验,以及大语言模型的分析能力,我们系统梳理了多年来苹果 WWDC 主题演讲的规律。在 WWDC 2025 即将揭幕之际,我们让 ChatGPT 对今年的 Keynote 内容进行了一个初步预测,聊作存档。等到明…...

Nuxt.js 中的路由配置详解
Nuxt.js 通过其内置的路由系统简化了应用的路由配置,使得开发者可以轻松地管理页面导航和 URL 结构。路由配置主要涉及页面组件的组织、动态路由的设置以及路由元信息的配置。 自动路由生成 Nuxt.js 会根据 pages 目录下的文件结构自动生成路由配置。每个文件都会对…...

Spring AI 入门:Java 开发者的生成式 AI 实践之路
一、Spring AI 简介 在人工智能技术快速迭代的今天,Spring AI 作为 Spring 生态系统的新生力量,正在成为 Java 开发者拥抱生成式 AI 的最佳选择。该框架通过模块化设计实现了与主流 AI 服务(如 OpenAI、Anthropic)的无缝对接&…...

自然语言处理——Transformer
自然语言处理——Transformer 自注意力机制多头注意力机制Transformer 虽然循环神经网络可以对具有序列特性的数据非常有效,它能挖掘数据中的时序信息以及语义信息,但是它有一个很大的缺陷——很难并行化。 我们可以考虑用CNN来替代RNN,但是…...

Unit 1 深度强化学习简介
Deep RL Course ——Unit 1 Introduction 从理论和实践层面深入学习深度强化学习。学会使用知名的深度强化学习库,例如 Stable Baselines3、RL Baselines3 Zoo、Sample Factory 和 CleanRL。在独特的环境中训练智能体,比如 SnowballFight、Huggy the Do…...

vue3+vite项目中使用.env文件环境变量方法
vue3vite项目中使用.env文件环境变量方法 .env文件作用命名规则常用的配置项示例使用方法注意事项在vite.config.js文件中读取环境变量方法 .env文件作用 .env 文件用于定义环境变量,这些变量可以在项目中通过 import.meta.env 进行访问。Vite 会自动加载这些环境变…...

C++八股 —— 单例模式
文章目录 1. 基本概念2. 设计要点3. 实现方式4. 详解懒汉模式 1. 基本概念 线程安全(Thread Safety) 线程安全是指在多线程环境下,某个函数、类或代码片段能够被多个线程同时调用时,仍能保证数据的一致性和逻辑的正确性…...

短视频矩阵系统文案创作功能开发实践,定制化开发
在短视频行业迅猛发展的当下,企业和个人创作者为了扩大影响力、提升传播效果,纷纷采用短视频矩阵运营策略,同时管理多个平台、多个账号的内容发布。然而,频繁的文案创作需求让运营者疲于应对,如何高效产出高质量文案成…...
