数据结构与算法系列之时间与空间复杂度

这里写目录标题
- 算法的复杂度
- 大O的渐进表示法
- 实例分析
- 空间复杂度
- 每日一题
算法的复杂度
衡量一个算法的好坏,一般 是从时间和空间两个维度来衡量的,
即时间复杂度和空间复杂度。
时间复杂度主要衡量一个算法的运行快慢,
空间复杂度主要衡量一个算法运行所需要的额外空间
大O的渐进表示法
1、用常数1取代运行时间中的所有加法常数。
2、在修改后的运行次数函数中,只保留最高阶项。
3、如果最高阶项存在且不是1,则去除与这个项目相乘的常数。得到的结果就是大O阶。//一般是大O的渐进表达法是运算的最坏情况,而且最好不要通过代码中有几层循环来判断如: 2N+10 时间复杂度为O(N)
M+N 时间复杂度为O(M+N)
(N*(N+1)/2 时间复杂度为O(N^2)
实例分析
这是一个关于二分的编码 ,把总元素看作N ,每循环一次都会少去一半的元素,共循环(logN)次这里在算法中底数为二(有些地方是lgN),所以时间复杂度为O(logN)
int BinarySearch(int* a, int n, int x)
{
assert(a);
int begin = 0;
int end = n-1;
while (begin <= end)
{
int mid = begin + ((end-begin)>>1);
if (a[mid] < x)
begin = mid+1;
else if (a[mid] > x)
end = mid-1;
else
return mid;
}
return -1;
}
这是关于斐波那契的递归 ,一个函数的时间复杂度为O(1),但是通过不断递归
如图所示所以时间复杂度为O(2^n)
long long Fib(size_t N)
{
if(N < 3)
return 1;
return Fib(N-1) + Fib(N-2);
}
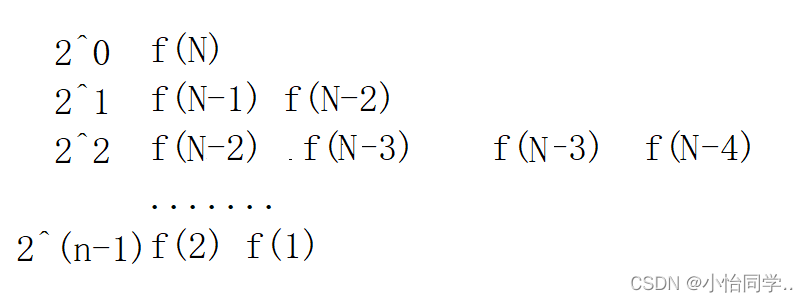
空间复杂度
空间复杂度大O渐进表示法来表示,主要是临时占用存储空间大小的量度
下列代码中主要开辟三个额外的变量,用大O表达式为O(1),因为代码中的数组是原本就有的,当函数被销毁时,函数的开辟的空间也不再存在
void BubbleSort(int* a, int n)
{
assert(a);
for (size_t end = n; end > 0; --end)
{int exchange = 0;
for (size_t i = 1; i < end; ++i)
{if (a[i-1] > a[i])
{Swap(&a[i-1], &a[i]);exchange = 1;
}
}
if (exchange == 0)break;
}
}
如图所示 由递归思想可知每递归,递到最后时 往回归嘛,函数栈会销毁
如fibArray[2] 销毁时,fibArray[1]会使用这个被销毁的空间 所以以此类推
大O表达式为(N)
long long* Fibonacci(size_t n)
{
if(n==0)
return NULL;
long long * fibArray = (long long *)malloc((n+1) * sizeof(long long));
fibArray[0] = 0;
fibArray[1] = 1;
for (int i = 2; i <= n ; ++i)
{
fibArray[i] = fibArray[i - 1] + fibArray [i - 2];
}
return fibArray;
}
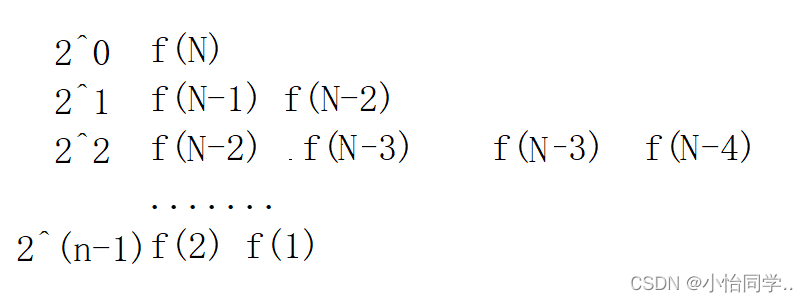
下列代码主要是递归思维 ,每次递归建立了一个栈帧
所以空间复杂度为(N)
long long Fac(size_t N)
{
if(N == 0)
return 1;
return Fac(N-1)*N;
}
每日一题
给定一个整数数组 nums,将数组中的元素向右轮转 k 个位置,其中 k 是非负数。
void swap(int left,int right,int*nums)
{int tmp =0;while(left < right){tmp = nums[left];nums[left] = nums[right];nums[right] = tmp;left++;right--;}}void rotate(int* nums, int numsSize, int k){
if(k > numsSize)
k = k%numsSize;//如果旋转数组大于numsSize swap(numsSize-k,numsSize-1,nums);//先逆序要旋转的
swap(0,numsSize-k-1,nums);//之后逆序不旋转的
swap(0,numsSize-1,nums);//最后整个数组在逆序一遍}

相关文章:

数据结构与算法系列之时间与空间复杂度
这里写目录标题算法的复杂度大O的渐进表示法实例分析空间复杂度每日一题算法的复杂度 衡量一个算法的好坏,一般 是从时间和空间两个维度来衡量的, 即时间复杂度和空间复杂度。 时间复杂度主要衡量一个算法的运行快慢, 空间复杂度主要衡量一个…...

Python代码使用PyQt5制作界面并封装
目录参考链接续:https://blog.csdn.net/yulinxx/article/details/93344163 若要对此程序进行封装,加个界面,然后制作成 EXE, 使用 PyQt5 制作界面,PyInstaller 进行封装成 EXE 可参考: Python制作小软件…...
【Node.js】MySQL数据库的第三方模块(mysql)
mysql安装操作MySQL数据库的第三方模块(mysql)通过第三方模块(mysql2)连接到MySQL数据库mysql插入数据mysql插入数据的便捷方式mysql更新数据mysql更新数据的便捷方式mysql删除数据安装操作MySQL数据库的第三方模块(my…...

Docker中安装并配置单机版redis
1、使用docker安装redis 搜索Reis镜像,这里展示的是官方最新的镜像docker search redis 使用官方dockerhub搜索redis 2、选用常用的redis5.0作为安装的版本docker pull redis:5.0 3、运行redis容器的两种方式 3.1 不映射外部配置文件直接运行redis5.0镜像docker …...

模拟微信聊天-课后程序(JAVA基础案例教程-黑马程序员编著-第八章-课后作业)
【案例9-1】 模拟微信聊天 【案例介绍】 1.案例描述 在如今,微信聊天已经人们生活中必不可少的重要组成部分,人们的交流很多都是通过微信来进行的。本案例要求:将多线程与UDP通信相关知识结合,模拟实现微信聊天小程序。通过监…...

html2canvas将页面dom元素内容渲染成图片保存至本地
html2canvas:https://html2canvas.hertzen.com/configuration/ github:https://github.com/niklasvh/html2canvas 效果 代码 <!DOCTYPE html> <html lang"en"><head><meta charset"UTF-8"><meta http-equiv"X-UA-Compa…...
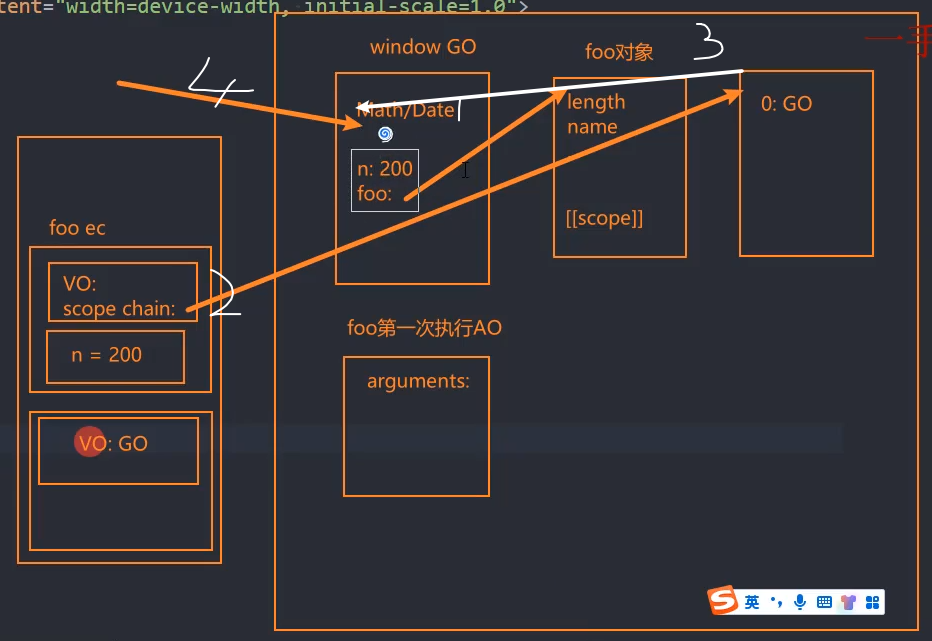
前端进阶JS运行原理
JS运行原理 深入了解V8引擎原理 浏览器内核是由两部分组成的,以webkit为例: WebCore:负责HTML解析、布局、渲染等等相关的工作;JavaScriptCore:解析、执行JavaScript代码; 官方对V8引擎的定义࿱…...
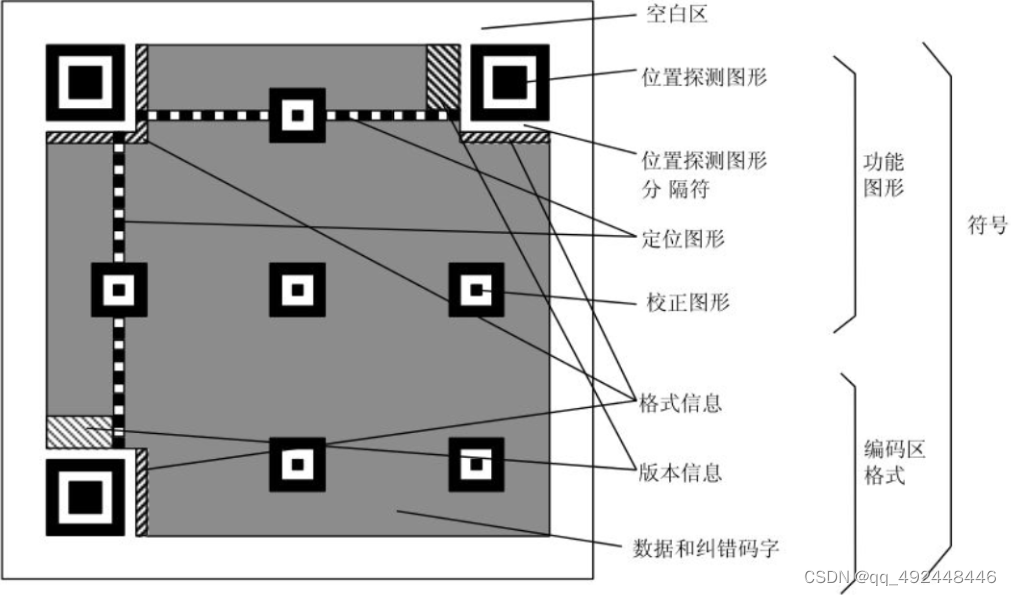
Python识别二维码的两种方法(cv2)
在学习Python处理二维码的过程中,我们看到的大多是“用python生成酷炫二维码”、“用Python制作动图二维码”之类的文章。而关于使用Python批量识别二维码的教程,并不多见。所以今天我会给大家分享两种批量识别二维码的Python技巧!pyzbar PI…...

用一个例子告诉你 怎样使用Spark中RDD的算子
目录 1. 前言 1.1 操作分类 1.2 语法知识 2. transformations 2.1 map 2.2 mapPartitions 2.3 flatMap 2.4 glom 2.5 groupBy 2.6 filter 2.7 sample 2.8 distinct 2.9 coalesce 2.10 repartition 2.11 sortBy 2.12 partitionBy 2.13 reduceByKey 2.14 gro…...
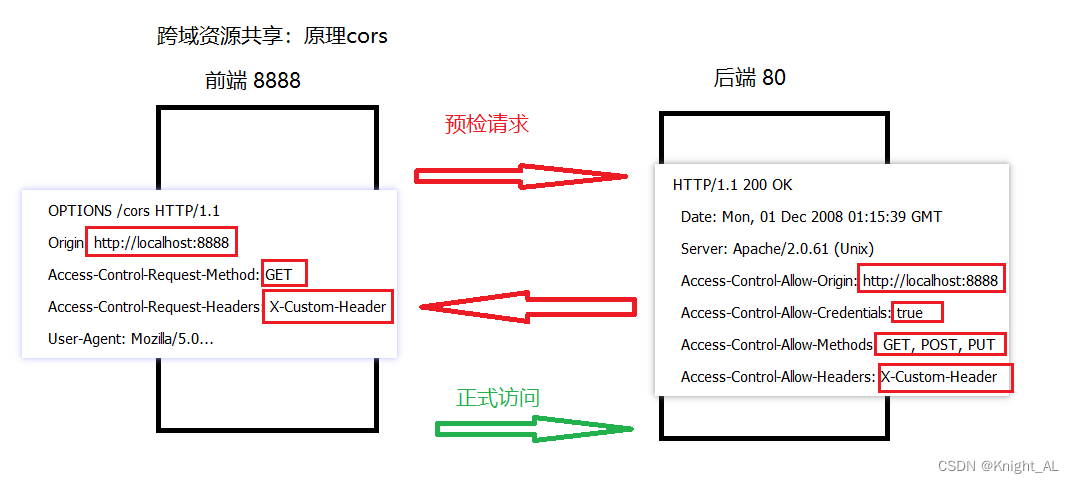
什么是跨域? 出现原因及解决方法
目录一、什么是跨域二、为什么有跨域问题?三、解决跨域问题的方案1.Jsonp2.nginx3.CORS3.1 什么是cors3.2 原理四、GateWay网关中实现跨域步骤一、什么是跨域 跨域:浏览器对于javascript的同源策略的限制 。 同源政策的目的,是为了保证用户…...

低代码系统能够解决哪些痛点?
低代码系统能够解决哪些痛点?如果用4句话去归纳,低代码开发可以解决以下问题—— 为企业提供更高的灵活性,用户可以突破代码的限制自主开发业务应用;通过减少对专业软件开发人员的依赖,公司可以快速响应市场上的新业务…...

华为OD机试题,用 Java 解【两数之和绝对值最小】问题
最近更新的博客 华为OD机试题,用 Java 解【停车场车辆统计】问题华为OD机试题,用 Java 解【字符串变换最小字符串】问题华为OD机试题,用 Java 解【计算最大乘积】问题华为OD机试题,用 Java 解【DNA 序列】问题华为OD机试 - 组成最大数(Java) | 机试题算法思路 【2023】使…...

AcWing算法提高课-3.1.1热浪
宣传一下算法提高课整理 <— CSDN个人主页:更好的阅读体验 <— 题目传送门点这里 题目描述 德克萨斯纯朴的民众们这个夏天正在遭受巨大的热浪!!! 他们的德克萨斯长角牛吃起来不错,可是它们并不是很擅长生产富…...

华为OD机试题【最差产品奖】用 C++ 编码,速通 (2023.Q1)
最近更新的博客 华为od 2023 | 什么是华为od,od 薪资待遇,od机试题清单华为OD机试真题大全,用 Python 解华为机试题 | 机试宝典【华为OD机试】全流程解析+经验分享,题型分享,防作弊指南华为od机试,独家整理 已参加机试人员的实战技巧文章目录 最近更新的博客使用说明最差产…...

NFT市场大战:Blur市场地位可持续吗?
在战胜无数虚张声势的挑战者之后,OpenSea终于迎来了一个实力雄厚的竞争对手,已威胁到它的市场主导地位。opensea是什么?参考《NFT,区块链的产物之一,了解NFT交易平台Opensea》 继成功的空投之后,Blur并没有…...

初识CSS
1.CSS语法形式CSS基本语法规则就是:选择器若干属性声明由选择器选择一个元素,其中的属性声明就作用于该元素.比如:<body><p>这是一个段落</p><!-- style可以放在代码的任意地方 --><style>p{/* 将字体颜色设置为红色 */color: red;}</style&g…...
知识总结(第3期))
kubernetes(k8s)知识总结(第3期)
1. PV 与 PVC PV 是持久卷(Persistent Volume)的首字母缩写。通常情况下,可以事先在 k8s 集群创建 PV 对象: apiVersion: v1 kind: PersistentVolume metadata:name: nfs spec:storageClassName: manualcapacity:storage: 1Giac…...

浅谈跨境电商运行模式
近些年,由于疫情的原因和人们的消费习惯的改变,线下销售越来越不占优势,电商行业由于这几年的飞速发展,成功地吸引到我国的民众,拼多多、淘宝、京东、天猫等各种各样的国内电商平台涌现,依靠着产品质量好、…...

Memcached
什么是MemcachedMemcached 是一个开源免费的高性能的分布式内存对象缓存系统、就是一个软件Memcached的作用缓存数据提高动态网站的速度Memcached的安装//方法一yum installmemcached//方法二1.安装libevent (memcached依赖包)tar -zvxflibevent-release-1.4.15-stable.tar.gzc…...
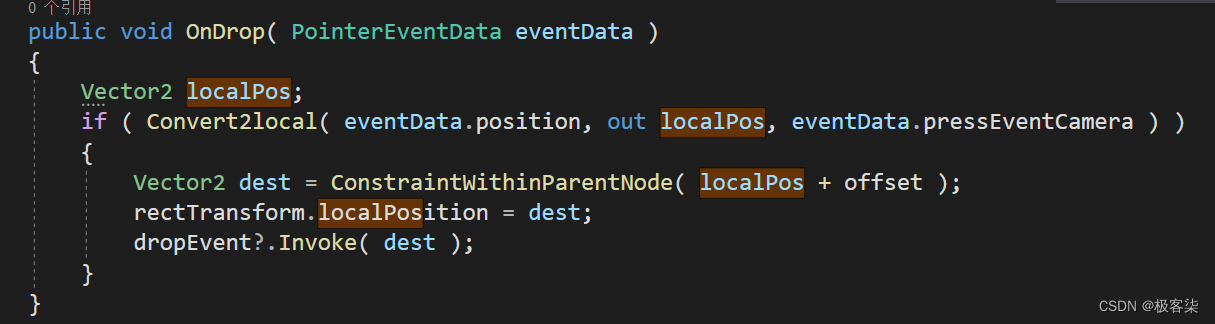
Unity UGUI 拖拽组件
效果展示 使用方式 拖到图片上即可用 父节点会约束它的活动范围哦~ 父节点会约束它的活动范围哦~ 父节点会约束它的活动范围哦~ 源码 using System.Collections; using System.Collections.Generic; using UnityEngine; using UnityEngine.EventSystems;/// <summary> /…...

IDEA运行Tomcat出现乱码问题解决汇总
最近正值期末周,有很多同学在写期末Java web作业时,运行tomcat出现乱码问题,经过多次解决与研究,我做了如下整理: 原因: IDEA本身编码与tomcat的编码与Windows编码不同导致,Windows 系统控制台…...

铭豹扩展坞 USB转网口 突然无法识别解决方法
当 USB 转网口扩展坞在一台笔记本上无法识别,但在其他电脑上正常工作时,问题通常出在笔记本自身或其与扩展坞的兼容性上。以下是系统化的定位思路和排查步骤,帮助你快速找到故障原因: 背景: 一个M-pard(铭豹)扩展坞的网卡突然无法识别了,扩展出来的三个USB接口正常。…...

Ubuntu系统下交叉编译openssl
一、参考资料 OpenSSL&&libcurl库的交叉编译 - hesetone - 博客园 二、准备工作 1. 编译环境 宿主机:Ubuntu 20.04.6 LTSHost:ARM32位交叉编译器:arm-linux-gnueabihf-gcc-11.1.0 2. 设置交叉编译工具链 在交叉编译之前&#x…...

C++初阶-list的底层
目录 1.std::list实现的所有代码 2.list的简单介绍 2.1实现list的类 2.2_list_iterator的实现 2.2.1_list_iterator实现的原因和好处 2.2.2_list_iterator实现 2.3_list_node的实现 2.3.1. 避免递归的模板依赖 2.3.2. 内存布局一致性 2.3.3. 类型安全的替代方案 2.3.…...

【Linux】shell脚本忽略错误继续执行
在 shell 脚本中,可以使用 set -e 命令来设置脚本在遇到错误时退出执行。如果你希望脚本忽略错误并继续执行,可以在脚本开头添加 set e 命令来取消该设置。 举例1 #!/bin/bash# 取消 set -e 的设置 set e# 执行命令,并忽略错误 rm somefile…...

基于距离变化能量开销动态调整的WSN低功耗拓扑控制开销算法matlab仿真
目录 1.程序功能描述 2.测试软件版本以及运行结果展示 3.核心程序 4.算法仿真参数 5.算法理论概述 6.参考文献 7.完整程序 1.程序功能描述 通过动态调整节点通信的能量开销,平衡网络负载,延长WSN生命周期。具体通过建立基于距离的能量消耗模型&am…...

K8S认证|CKS题库+答案| 11. AppArmor
目录 11. AppArmor 免费获取并激活 CKA_v1.31_模拟系统 题目 开始操作: 1)、切换集群 2)、切换节点 3)、切换到 apparmor 的目录 4)、执行 apparmor 策略模块 5)、修改 pod 文件 6)、…...

学习STC51单片机31(芯片为STC89C52RCRC)OLED显示屏1
每日一言 生活的美好,总是藏在那些你咬牙坚持的日子里。 硬件:OLED 以后要用到OLED的时候找到这个文件 OLED的设备地址 SSD1306"SSD" 是品牌缩写,"1306" 是产品编号。 驱动 OLED 屏幕的 IIC 总线数据传输格式 示意图 …...

基于Java Swing的电子通讯录设计与实现:附系统托盘功能代码详解
JAVASQL电子通讯录带系统托盘 一、系统概述 本电子通讯录系统采用Java Swing开发桌面应用,结合SQLite数据库实现联系人管理功能,并集成系统托盘功能提升用户体验。系统支持联系人的增删改查、分组管理、搜索过滤等功能,同时可以最小化到系统…...
:观察者模式)
JS设计模式(4):观察者模式
JS设计模式(4):观察者模式 一、引入 在开发中,我们经常会遇到这样的场景:一个对象的状态变化需要自动通知其他对象,比如: 电商平台中,商品库存变化时需要通知所有订阅该商品的用户;新闻网站中࿰…...
