深度学习常用的激活函数总结
各种激活函数总结
目录
- 一、sigmoid
- 二、tanh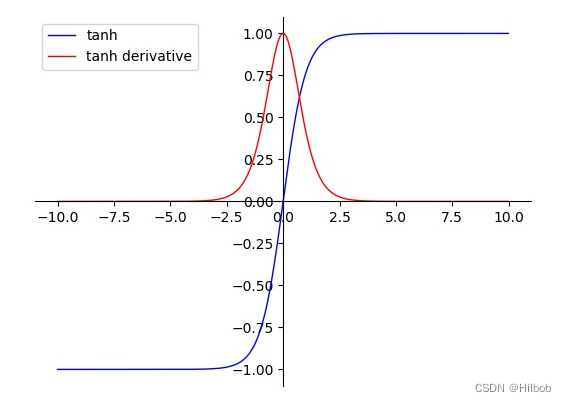
- 三、ReLU系列
- 1.原始ReLU
- 2.ReLU改进:Leaky ReLU
- 四、swish
- 五、GeLU
一、sigmoid

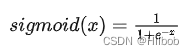
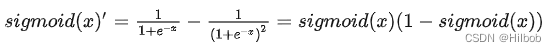
优点:
1.可以将任意范围的输出映射到 (0, 1) 范围内,表示它对每个神经元的输出进行了归一化,适合用于将概率作为输出的模型。
2.易于求导缺点
1.计算量大;
2.Sigmoid导数取值范围是[0, 0.25],且当x过大或过小时,sigmoid函数的导数接近于0,由于神经网络反向传播时的“链式反应”,容易造成梯度消失,难以更新网路参数。高层网络的误差相对第一层卷积的参数的梯度将是一个非常小的值,这就是所谓的“梯度消失”。
3.Sigmoid的输出不是0均值(即zero-centered);这会导致后一层的神经元将得到上一层输出的非0均值的信号作为输入,随着网络的加深,会改变数据的原始分布。
二、tanh
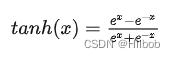
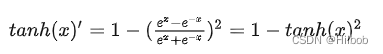
优点:
1.tanh的输出范围时(-1, 1),解决了sigmoid不是0均值输出问题;
2.在靠近0处的导数值较sigmoid更大,即神经网络的收敛速度相对于sigmoid更快;
3.在一般的分类问题中,可将tanh用于隐藏层,sigmoid 函数用于输出层。
缺点:
1.计算量大;
2.tanh导数范围在(0, 1)之间,相比sigmoid导数的范围(0, 0.25),梯度消失问题会得到缓解,但仍然存在。
三、ReLU系列
1.原始ReLU
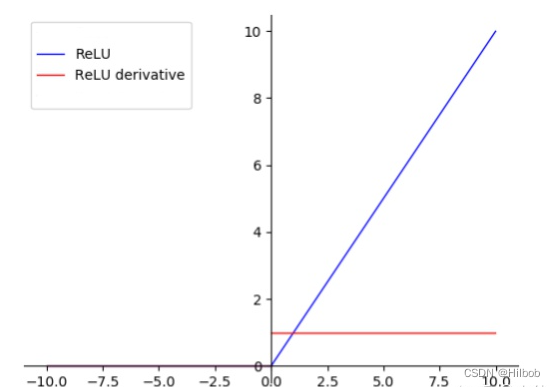
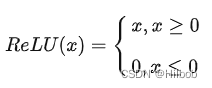
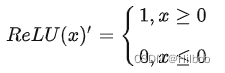
优点:
1.计算速度更快;
2.ReLU是非线性函数(所谓非线性,就是一阶导数不为常数;对ReLU求导,在输入值分别为正和为负的情况下,导数是不同的,即ReLU的导数不是常数,所以ReLU是非线性的,只是不同于sigmoid和tanh,ReLU的非线性不是光滑的);
2.梯度只有 0, 1 两个常量,有效地解决梯度消失的问题。
3.ReLU的单侧抑制(当ReLU的输入x为负时,ReLU输出为0)提供了网络的稀疏表达能力。(深度学习是根据大批量样本数据,从错综复杂的数据关系中,找到关键信息。换句话说,就是把密集矩阵转化为稀疏矩阵,去除噪音,保留数据的关键信息,这样的模型就有了鲁棒性。ReLU将x<0的输出置为0,就是一个去噪音,稀疏矩阵的过程。而且在训练过程中,这种稀疏性是动态调节的,网络会自动调整稀疏比例,保证矩阵具备最优的关键特征。)
缺点:
1.ReLU 函数不是zero-centered输出;。
2.训练过程中会导致神经元死亡的问题,即ReLU 强制将<0的输入置为0(屏蔽该特征),导致网络的部分神经元处于无法更新的状态,这种现象称为死亡 ReLU 问题 (Dying ReLU
Problem);
3.虽然采用ReLU在“链式反应”中不会出现梯度消失,但梯度下降的幅值就完全取决于权值的乘积,这样可能会出现梯度爆炸问题。 可以通过以下两种思路解决这类问题:一是控制权值的大小,让权值在(0,1)范围内;二是做梯度裁剪,控制梯度下降强度,如ReLU(x)=min(6, max(0,x))。
2.ReLU改进:Leaky ReLU
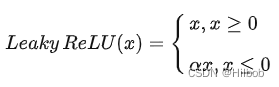
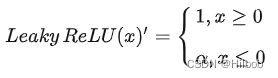
优点:
1.解决了ReLU的神经元死亡问题。Leaky ReLU中引入了超参数,一般设置为0.01。在反向传播过程中,对于Leaky ReLU的输入小于零的情况,也可以计算得到一个梯度(而不是像ReLU一样值为0)。
缺点:
1.相较于ReLU,神经网络的稀疏性要差一些;
2.引入了额外的超参数。
四、swish
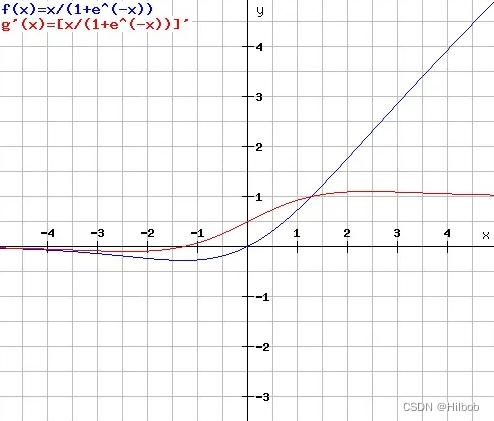
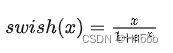
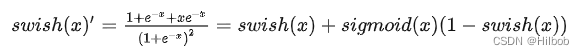
优点:
1.Swish是通过NAS搜索得到的,其取值范围是[-0.278, +∞),且平滑、非单调;
2.Swish 在深层模型上的效果优于 ReLU。例如,仅仅使用 Swish 单元替换 ReLU 就能把 Mobile NASNetA 在 ImageNet 上的 top-1 分类准确率提高 0.9%,Inception-ResNet-v 的分类准确率提高 0.6%。
缺点:
1.计算量大
五、GeLU
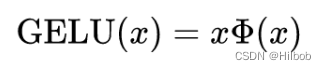
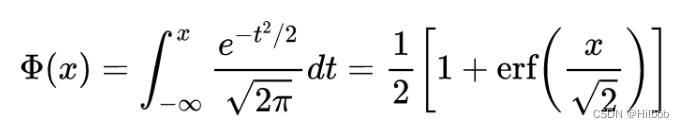
erf为高斯误差函数:
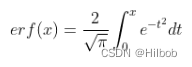
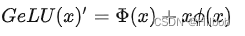
优点:
受 Dropout、ReLU 等机制的影响,希望将神经网络中不重要的激活信息置为零。可以理解为,对于输入的值,我们根据它的情况乘上 1 或
0。更「数学」一点的描述是,对于每一个输入 x,其服从于标准正态分布N(0, 1),它会乘上一个伯努利分布Bernoulli(Φ(x)),其中Φ(x) = P(X ≤ x)。随着 x 的降低,它被归零的概率会升高。对于 ReLU来说,这个界限就是 0,输入小于零就会被归零。这一类激活函数,不仅保留了概率性,同时也保留了对输入的依赖性。
我们经常希望神经网络具有确定性决策,这种想法催生了 GELU 激活函数的诞生。这种函数的非线性希望对输入 x上的随机正则化项做一个转换,具体来说可以表示为:Φ(x)×1×x+(1−Φ(x))×0×x=xΦ(x)Φ(x) × 1 × x + (1 − Φ(x)) × 0 × x = xΦ(x)Φ(x)×1×x+(1−Φ(x))×0×x=xΦ(x)。我们可以理解为,对于一部分Φ(x),它直接乘以输入 x,而对于另一部分 (1 −Φ(x)),它们需要归零。不太严格地说,上面这个表达式可以按当前输入 x 比其它输入大多少来缩放 x。GeLU取值范围(-0.17,+∞),平滑、非单调,似乎是 NLP 领域的当前最佳,尤其在 Transformer 模型中表现最好,被GPT-2、BERT、RoBERTa、ALBERT 等NLP模型所采用;
缺点:
计算量大,通常采用GeLU的近似式来代替原式计算,源论文给出了两个近似:
参考文献:
https://zhuanlan.zhihu.com/p/450361606
相关文章:

深度学习常用的激活函数总结
各种激活函数总结 目录一、sigmoid二、tanh三、ReLU系列1.原始ReLU2.ReLU改进:Leaky ReLU四、swish五、GeLU一、sigmoid 优点: 1.可以将任意范围的输出映射到 …...
)
Java编程问题top100---基础语法系列(二)
Java编程问题top100---基础语法系列(二)六、如何测试一个数组是否包含指定的值?简单且优雅的方法:自己动手写逻辑对象数组JDK 8 APIJDK 9 API Set.of()七、重写(Override)equlas和hashCode方法时应考虑的问题理论上讲&…...
网页打印与导出word实现在A4纸上相同效果
在工作中遇到这样一个需求,客户要求: 1、实现在浏览器中打印和导出到word中,要求浏览器打印出来的效果和word中打印的效果基本一致。2、打印的内容要自动分页,第一页的顶部有文件头,最后一页的底部有页尾。 这里记录一…...

备战英语6级——记录复习进度
开始记录—— 学习:如何记录笔记? 1:首先我认为:电脑打字比较适合我! 2:先记笔记,再“填笔记”! 记笔记就是一个框架,记录一个大概的东西。后面需要在笔记中࿰…...
实例10:四足机器人运动学逆解可视化与实践
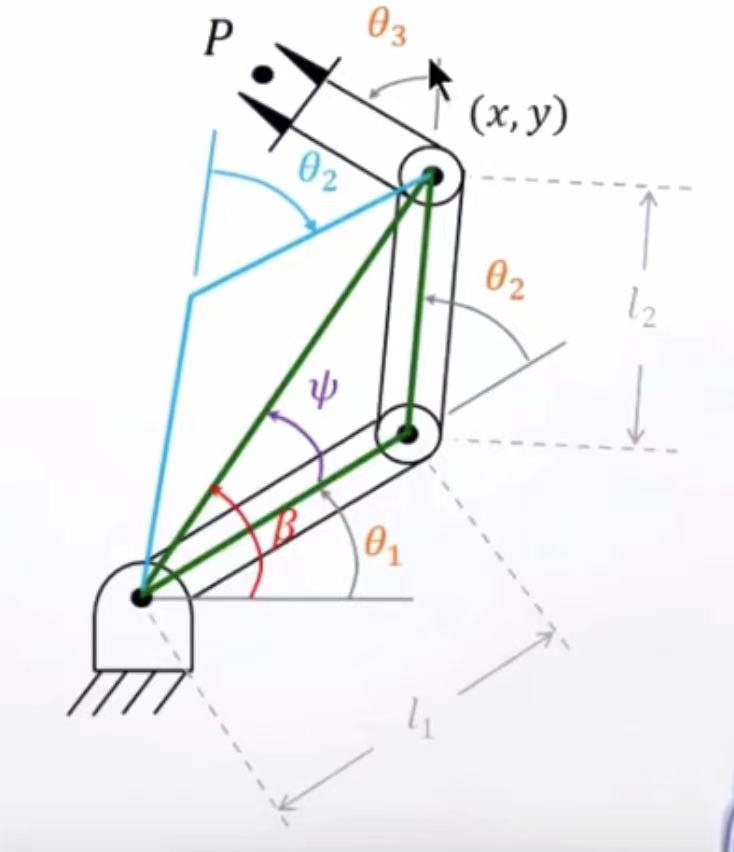
实例10: 四足机器人运动学逆解单腿可视化 实验目的 了解逆运动学的有无解、有无多解情况。了解运动学逆解的求解。熟悉逆运动学中求解的几何法和代数法。熟悉单腿舵机的简单校准。掌握可视化逆向运动学计算结果的方法。 实验要求 拼装一条mini pupper的腿部。运…...

Elasticsearch7.8.0版本优化——路由选择
目录一、Elasticsearch 如何知道一个文档存放在哪个分片二、不带 routing 查询三、带 routing 查询一、Elasticsearch 如何知道一个文档存放在哪个分片 其实是通过这个公式来计算出来:shard hash(routing) % number_of_primary_shardsrouting 默认值是文档的 id&a…...

Go常量的定义和使用const,const特性“隐式重复前一个表达式”,以及iota枚举常量的使用
Go常量的定义和使用const,以及iota枚举常量的使用Go常量constGo中常量的定义和使用Go特性const,"隐式重复前一个表达式"iota 实现枚举常量Go常量const Go语言中的const整合了C语言中的宏定义常量,const只读变量枚举变量 绝大多数情况下,Go常…...
Git学习(1)pro git阅读
目录 目录: 1. 起步 2. Git 基础 3. Git 分支 4. 服务器上的 Git 5. 分布式 Git 第一章 1.3 Git是什么 1.6运行git前的配置 该开源图书网站 Git - Book (git-scm.com) 目录: 1. 起步 1.1 关于版本控制1.2 Git 简史1.3 Git 是什么?1…...
PHY自协商
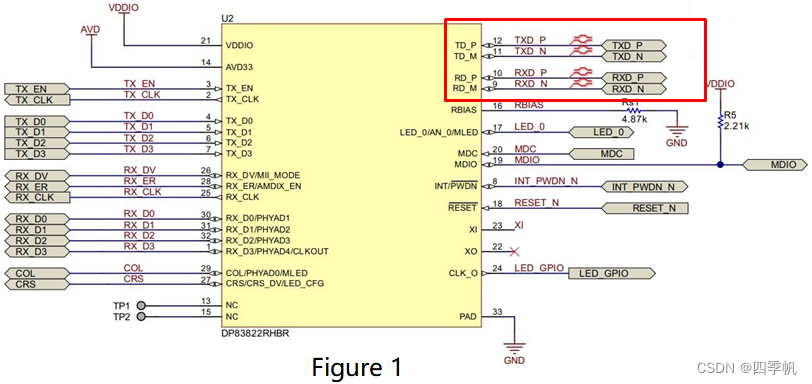
1. 自协商定义 自动协商模式是端口根据另一端设备的连接速度和双工模式,自动把它的速度调节到最高的公共水平,即线路两端能具有的最快速度和双工模式。 自协商功能允许一个网络设备能够将自己所支持的工作模式信息传达给网络上的对端,并接受对…...

【大数据离线开发】8.2 Hive的安装和配置
8.3 Hive的安装和配置 安装模式: 嵌入模式 :不需要使用MySQL,需要Hive自带的一个关系型数据库:Derby本地模式、远程模式 ----> 需要MySQL数据库的支持 安装 hive 安装包 1、解压tar -zxvf apache-hive-2.3.0-bin.tar.gz -C…...

Capture Modules:车载网络报文捕获模块
(以下所有图片均来源于Technica官网) Technica Engineering的新一代硬件设备,即Capture Modules,提供了五种变体以涵盖不同带宽的车载以太网(100BASE-T1和1000BASE-T1)以及常见的IVN技术(CAN、C…...

数据结构与算法系列之时间与空间复杂度
这里写目录标题算法的复杂度大O的渐进表示法实例分析空间复杂度每日一题算法的复杂度 衡量一个算法的好坏,一般 是从时间和空间两个维度来衡量的, 即时间复杂度和空间复杂度。 时间复杂度主要衡量一个算法的运行快慢, 空间复杂度主要衡量一个…...

Python代码使用PyQt5制作界面并封装
目录参考链接续:https://blog.csdn.net/yulinxx/article/details/93344163 若要对此程序进行封装,加个界面,然后制作成 EXE, 使用 PyQt5 制作界面,PyInstaller 进行封装成 EXE 可参考: Python制作小软件…...
【Node.js】MySQL数据库的第三方模块(mysql)
mysql安装操作MySQL数据库的第三方模块(mysql)通过第三方模块(mysql2)连接到MySQL数据库mysql插入数据mysql插入数据的便捷方式mysql更新数据mysql更新数据的便捷方式mysql删除数据安装操作MySQL数据库的第三方模块(my…...

Docker中安装并配置单机版redis
1、使用docker安装redis 搜索Reis镜像,这里展示的是官方最新的镜像docker search redis 使用官方dockerhub搜索redis 2、选用常用的redis5.0作为安装的版本docker pull redis:5.0 3、运行redis容器的两种方式 3.1 不映射外部配置文件直接运行redis5.0镜像docker …...

模拟微信聊天-课后程序(JAVA基础案例教程-黑马程序员编著-第八章-课后作业)
【案例9-1】 模拟微信聊天 【案例介绍】 1.案例描述 在如今,微信聊天已经人们生活中必不可少的重要组成部分,人们的交流很多都是通过微信来进行的。本案例要求:将多线程与UDP通信相关知识结合,模拟实现微信聊天小程序。通过监…...

html2canvas将页面dom元素内容渲染成图片保存至本地
html2canvas:https://html2canvas.hertzen.com/configuration/ github:https://github.com/niklasvh/html2canvas 效果 代码 <!DOCTYPE html> <html lang"en"><head><meta charset"UTF-8"><meta http-equiv"X-UA-Compa…...
前端进阶JS运行原理
JS运行原理 深入了解V8引擎原理 浏览器内核是由两部分组成的,以webkit为例: WebCore:负责HTML解析、布局、渲染等等相关的工作;JavaScriptCore:解析、执行JavaScript代码; 官方对V8引擎的定义࿱…...
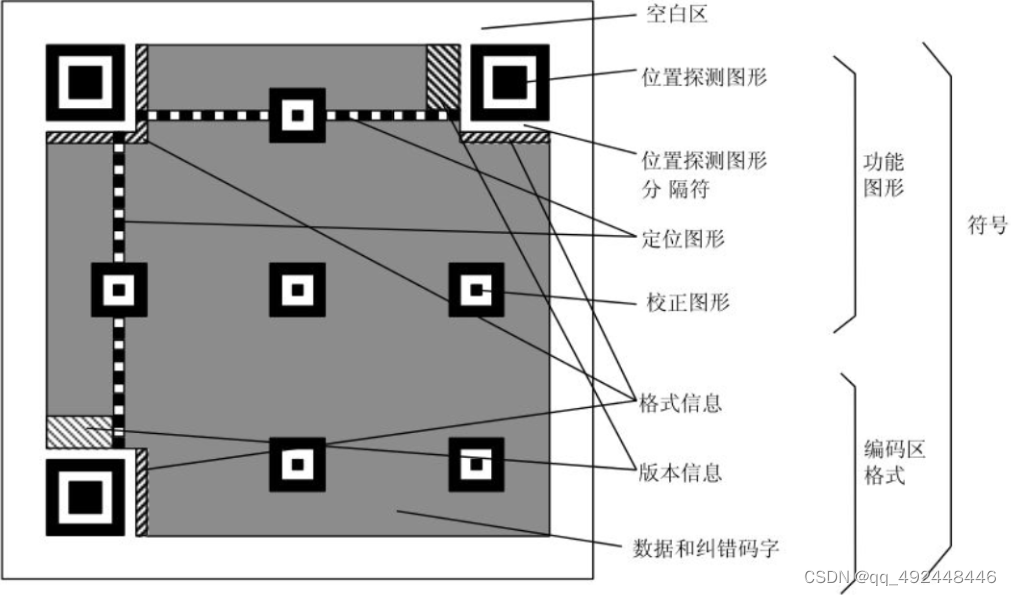
Python识别二维码的两种方法(cv2)
在学习Python处理二维码的过程中,我们看到的大多是“用python生成酷炫二维码”、“用Python制作动图二维码”之类的文章。而关于使用Python批量识别二维码的教程,并不多见。所以今天我会给大家分享两种批量识别二维码的Python技巧!pyzbar PI…...

用一个例子告诉你 怎样使用Spark中RDD的算子
目录 1. 前言 1.1 操作分类 1.2 语法知识 2. transformations 2.1 map 2.2 mapPartitions 2.3 flatMap 2.4 glom 2.5 groupBy 2.6 filter 2.7 sample 2.8 distinct 2.9 coalesce 2.10 repartition 2.11 sortBy 2.12 partitionBy 2.13 reduceByKey 2.14 gro…...

eNSP-Cloud(实现本地电脑与eNSP内设备之间通信)
说明: 想象一下,你正在用eNSP搭建一个虚拟的网络世界,里面有虚拟的路由器、交换机、电脑(PC)等等。这些设备都在你的电脑里面“运行”,它们之间可以互相通信,就像一个封闭的小王国。 但是&#…...

【网络】每天掌握一个Linux命令 - iftop
在Linux系统中,iftop是网络管理的得力助手,能实时监控网络流量、连接情况等,帮助排查网络异常。接下来从多方面详细介绍它。 目录 【网络】每天掌握一个Linux命令 - iftop工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景…...
)
进程地址空间(比特课总结)
一、进程地址空间 1. 环境变量 1 )⽤户级环境变量与系统级环境变量 全局属性:环境变量具有全局属性,会被⼦进程继承。例如当bash启动⼦进程时,环 境变量会⾃动传递给⼦进程。 本地变量限制:本地变量只在当前进程(ba…...
)
椭圆曲线密码学(ECC)
一、ECC算法概述 椭圆曲线密码学(Elliptic Curve Cryptography)是基于椭圆曲线数学理论的公钥密码系统,由Neal Koblitz和Victor Miller在1985年独立提出。相比RSA,ECC在相同安全强度下密钥更短(256位ECC ≈ 3072位RSA…...
使用rpicam-app通过网络流式传输视频)
树莓派超全系列教程文档--(62)使用rpicam-app通过网络流式传输视频
使用rpicam-app通过网络流式传输视频 使用 rpicam-app 通过网络流式传输视频UDPTCPRTSPlibavGStreamerRTPlibcamerasrc GStreamer 元素 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 使用 rpicam-app 通过网络流式传输视频 本节介绍来自 rpica…...

如何在看板中体现优先级变化
在看板中有效体现优先级变化的关键措施包括:采用颜色或标签标识优先级、设置任务排序规则、使用独立的优先级列或泳道、结合自动化规则同步优先级变化、建立定期的优先级审查流程。其中,设置任务排序规则尤其重要,因为它让看板视觉上直观地体…...

聊聊 Pulsar:Producer 源码解析
一、前言 Apache Pulsar 是一个企业级的开源分布式消息传递平台,以其高性能、可扩展性和存储计算分离架构在消息队列和流处理领域独树一帜。在 Pulsar 的核心架构中,Producer(生产者) 是连接客户端应用与消息队列的第一步。生产者…...

智能在线客服平台:数字化时代企业连接用户的 AI 中枢
随着互联网技术的飞速发展,消费者期望能够随时随地与企业进行交流。在线客服平台作为连接企业与客户的重要桥梁,不仅优化了客户体验,还提升了企业的服务效率和市场竞争力。本文将探讨在线客服平台的重要性、技术进展、实际应用,并…...

DIY|Mac 搭建 ESP-IDF 开发环境及编译小智 AI
前一阵子在百度 AI 开发者大会上,看到基于小智 AI DIY 玩具的演示,感觉有点意思,想着自己也来试试。 如果只是想烧录现成的固件,乐鑫官方除了提供了 Windows 版本的 Flash 下载工具 之外,还提供了基于网页版的 ESP LA…...

AI编程--插件对比分析:CodeRider、GitHub Copilot及其他
AI编程插件对比分析:CodeRider、GitHub Copilot及其他 随着人工智能技术的快速发展,AI编程插件已成为提升开发者生产力的重要工具。CodeRider和GitHub Copilot作为市场上的领先者,分别以其独特的特性和生态系统吸引了大量开发者。本文将从功…...