[数据结构]-AVL树

前言

作者：小蜗牛向前冲

名言：我可以接受失败，但我不能接受放弃

  如果觉的博主的文章还不错的话，还请点赞，收藏，关注👀支持博主。如果发现有问题的地方欢迎❀大家在评论区指正

目录

一、AVL树基本知识

1、概念

2、节点定义

3、插入

二、AVL树的旋转

1、右单旋

2、左单旋

 3、左右双旋

4、 右左双旋

三、AVL树的测试 

1、测试的补充代码

2、测试 

---

 本期学习目标：清楚什么是AVL树，模拟实现AVL树，理解四种旋转模型。 

一、AVL树基本知识

1、概念

       二叉搜索树虽可以缩短查找的效率，但如果数据有序或接近有序二叉搜索树将退化为单支树，查 找元素相当于在顺序表中搜索元素，效率低下。因此，两位俄罗斯的数学家G.M.Adelson-Velskii 和E.M.Landis在1962年 发明了一种解决上述问题的方法：当向二叉搜索树中插入新结点后，如果能保证每个结点的左右 子树高度之差的绝对值不超过1(需要对树中的结点进行调整)，即可降低树的高度，从而减少平均 搜索长度。

一棵AVL树或者是空树，或者是具有以下性质的二叉搜索树：

• 它的左右子树都是AVL树
• 左右子树高度之差(简称平衡因子)的绝对值不超过1(-1/0/1)

 

2、节点定义

template<class k,class v>
struct AVLTreeNode
{pair<k, v>_kv;AVLTreeNode<k, v>* _left;AVLTreeNode<k, v>* _right;AVLTreeNode<k, v>* _parent;int _bf;//balance factor//带参数的构造函数AVLTreeNode(const pair<k,v>& kv):_kv(kv),_left(nullptr),_right(nullptr),_parent(nullptr),_bf(0){}
};

这里我们定义了三叉链来定义节点，最为特殊的是我们相对于二叉树，我们多了一个平衡 因子，这是维持AVL特性的关键，下面我们将围绕此展开对AVL树的构建。

注意：平衡因子 = 右树的高度-左树的高度

3、插入

AVL树就是在二叉搜索树的基础上引入了平衡因子，因此AVL树也可以看成是二叉搜索树。那么 AVL树的插入过程可以分为两步：

1. 按照二叉搜索树的方式插入新节点

2. 调整节点的平衡因子

对于插入最为重要的是平衡因子的更新，下面我们将讨论更新平衡因子情况：

是否要在更新平衡因子，要根据子树的高度：
1、如果parent->_bf==0,者说明以前的parent->_bf==-1或者parent->_bf==1
即是以前是一边高一边低，现在是插入到矮的一边，树的高度不变，不更新

2、如果parent->_bf==-1或者parent->_bf==-1，者以前parent->_bf==0
即是以前树是均衡的，现在插入让一边高了
子树的高度变了，要向上更新

3 、如果parent->_bf==-2或者parent->_bf==2，者以前parent->_bf==-1或者parent->_bf==1
现在树严重不平衡，让树旋转维持结构

//插入
bool Insert(const pair<k, v>& kv)
{if (_root == nullptr){_root = new Node(kv);return true;}Node* parent = nullptr;Node* cur = _root;//找插入位置while (cur){//插入元素大于比较元素if (cur->_kv.first < kv.first){parent = cur;//继续往右树走cur = cur->_right;}else if (cur->_kv.first > kv.first){parent = cur;//继续往左树走cur = cur->_left;}else//插入元素于树中元素相等，不插入{return false;}}cur = new Node(kv);//链接节点if (parent->_kv.first > kv.first){parent->_left = cur;//更新parentcur->_parent = parent;}else{parent->_right = cur;//更新parentcur->_parent = parent;}//更新平衡因子while (parent)//parent为空，就更新到了根{//新增在树节点左边，parent->bf--//新增在树节点右边，parent->bf++if (cur == parent->_left){parent->_bf--;}else{parent->_bf++;}//是否要在更新平衡因子，要根据子树的高度：//1、如果parent->_bf==0,者说明以前的parent->_bf==-1或者parent->_bf==1//即是以前是一边高一边低，现在是插入到矮的一边，树的高度不变，不更新//2、如果parent->_bf==-1或者parent->_bf==-1，者以前parent->_bf==0//即是以前树是均衡的，现在插入让一边高了//子树的高度变了，要向上更新//3 、如果parent->_bf==-2或者parent->_bf==2，者以前parent->_bf==-1或者parent->_bf==1//现在树严重不平衡，让树旋转维持结构//旋转：//1、让子树的高度差不差过1//2、旋转过程中也要保存搜索树结构//3、边更新平衡因子//4、让这课树的高度保存和之前一样(旋转结束，不影响上层结构)if (parent->_bf == 0){break;}else if (parent->_bf == -1 || parent->_bf == 1){cur = parent;parent = parent->_parent;}//旋转else if (parent->_bf == -2 || parent->_bf == 2){//左单旋转if (parent->_bf == 2 && cur->_bf == 1){RotateL(parent);}//右单旋else if (parent->_bf == -2 && cur->_bf == -1){RotateR(parent);}//左右双旋else if (parent->_bf == -2 && cur->_bf == 1){RotateLR(parent);}//右左双旋else if (parent->_bf == 2 && cur->_bf == -1){RotateRL(parent);}else{assert(false);}//旋转完成,平衡因子已经更新跳出循环break;}else{assert(false);}}
}

二、AVL树的旋转

如果parent->_bf==-2或者parent->_bf==2，者以前parent->_bf==-1或者parent->_bf==1
现在树严重不平衡，让树旋转维持结构：

旋转的要求：

• 让子树的高度差不差过1
• 旋转过程中也要保存搜索树结构
• 边更新平衡因子
• 让这课树的高度保存和之前一样(旋转结束，不影响上层结构)

旋转的分类： 

• 新节点插入较高左子树的左侧—左左：右单旋
• 新节点插入较高右子树的右侧—右右：左单旋
• 新节点插入较高左子树的右侧—左右：先左单旋再右单旋
• 新节点插入较高右子树的左侧—右左：先右单旋再左单旋

1、右单旋

对于可能出现右旋转的情况的子树是多样的

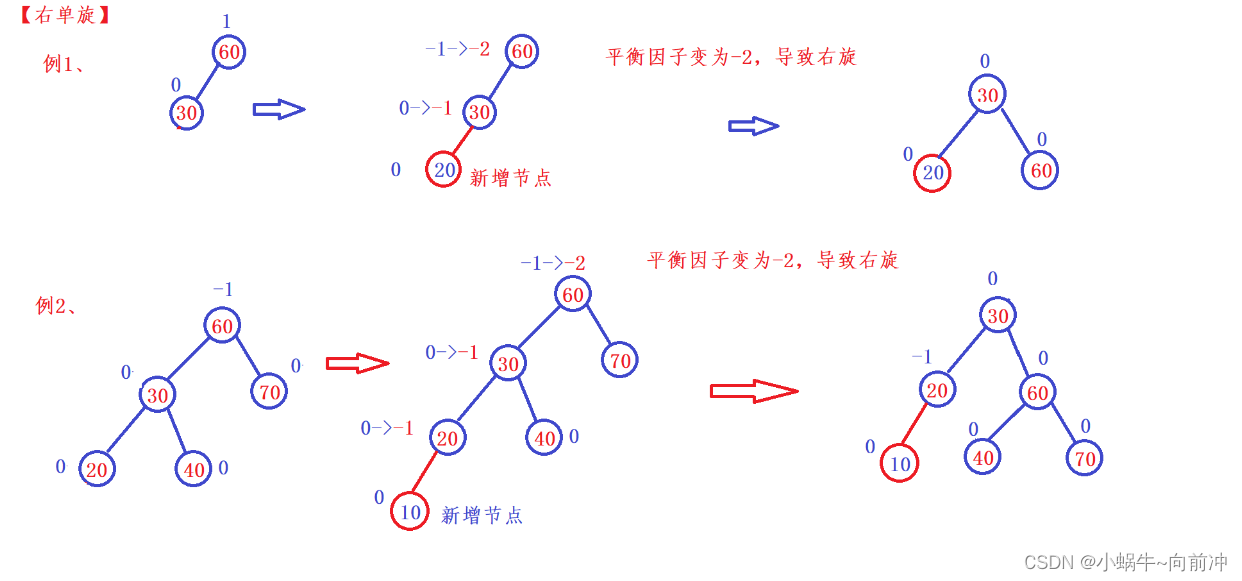
 这里我们可以根据需要进行右单旋转抽像图进行理解

 

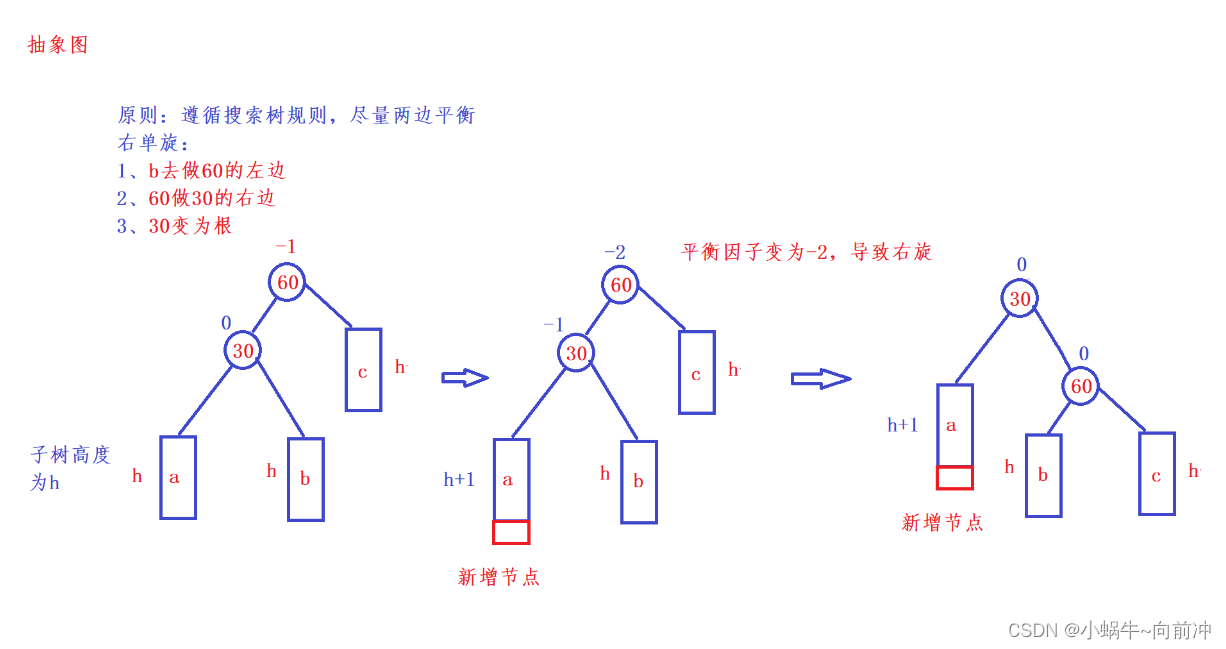
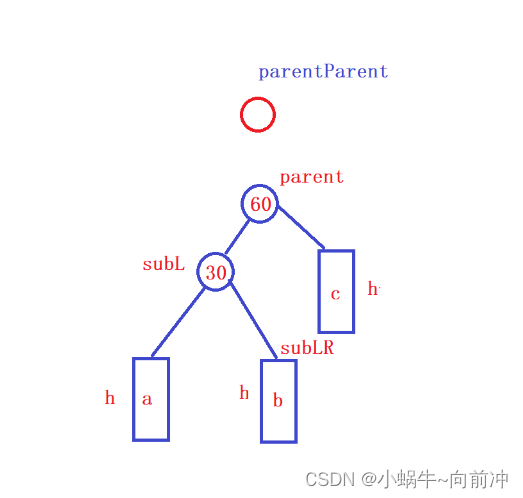
代码实现： 

//右单旋
void RotateR(Node* parent)
{Node* subL = parent->_left;Node* subLR = subL->_right;//b做60的右parent->_left = subLR;if (subLR){subLR->_parent = parent;}Node* ppNode = parent->_parent;//60做30的右subL->_right = parent;parent->_parent = subL;//60就是以前的根节点if (ppNode == nullptr){_root = subL;subL->_parent = ppNode;}else{//上层父节点的左边是子树的parentif (ppNode->_left == parent){ppNode->_left = subL;}else{ppNode->_right = subL;}subL->_parent = ppNode;}//更新平衡因子parent->_bf = subL->_bf = 0;
}

2、左单旋

 

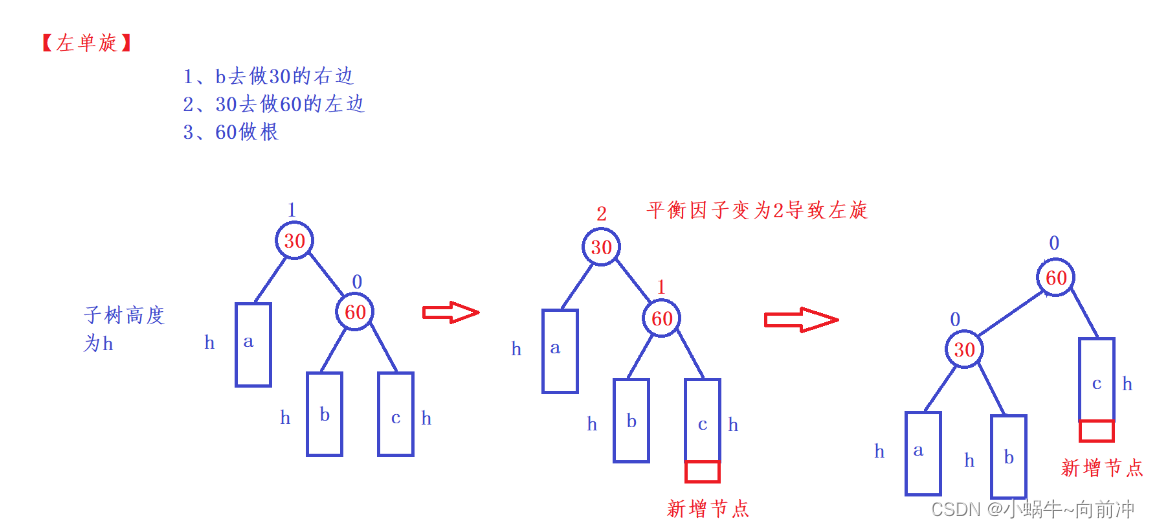
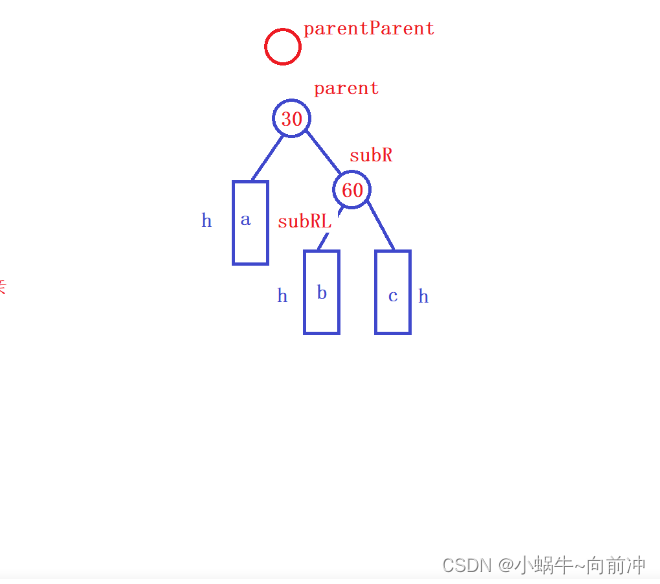
代码实现：

 

void RotateL(Node * parent)
{Node* subR = parent->_right;//父节点的右子树Node* subRL = subR->_left;//右树的左树//让60左边链接到30的右边parent->_right = subRL;if (subRL){subRL->_parent = parent;}Node* ppNode = parent->_parent;//让30变成60的左边subR->_left = parent;parent->_parent = subR;//subR就是根节点if (ppNode == nullptr){_root = subR;_root->_parent = nullptr;}else{//上层父节点的左边是子树的parentif (ppNode->_left == parent){ppNode->_left = subR;}else{ppNode->_right = subR;}//子树父节点和上层父节点链接subR->_parent = ppNode;}//更新平衡因子parent->_bf = subR->_bf = 0;
}

 3、左右双旋

对于双旋转来说：节点新增的位置不同，平衡因子最终也会不同，这里我们要进行分类讨论：

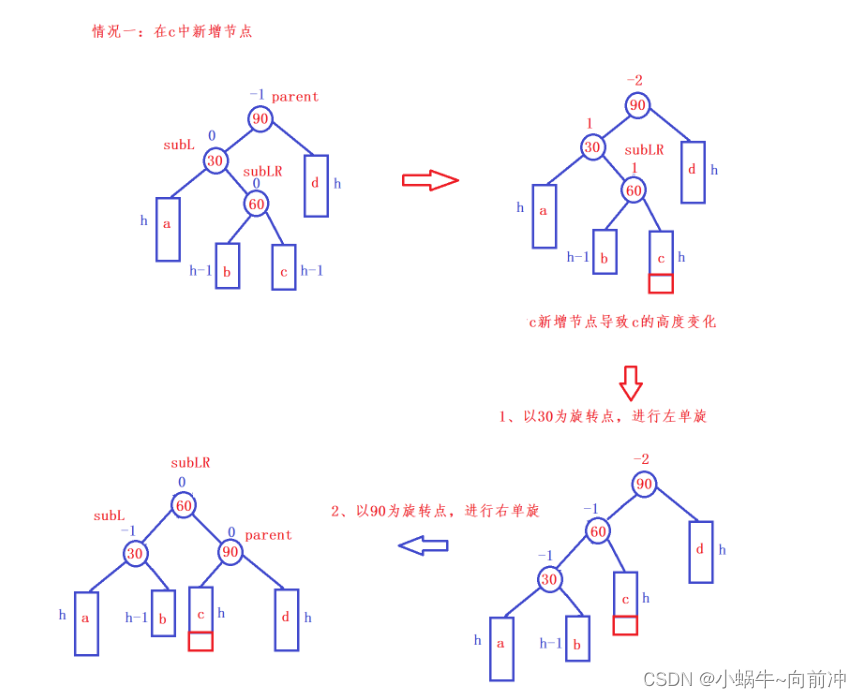
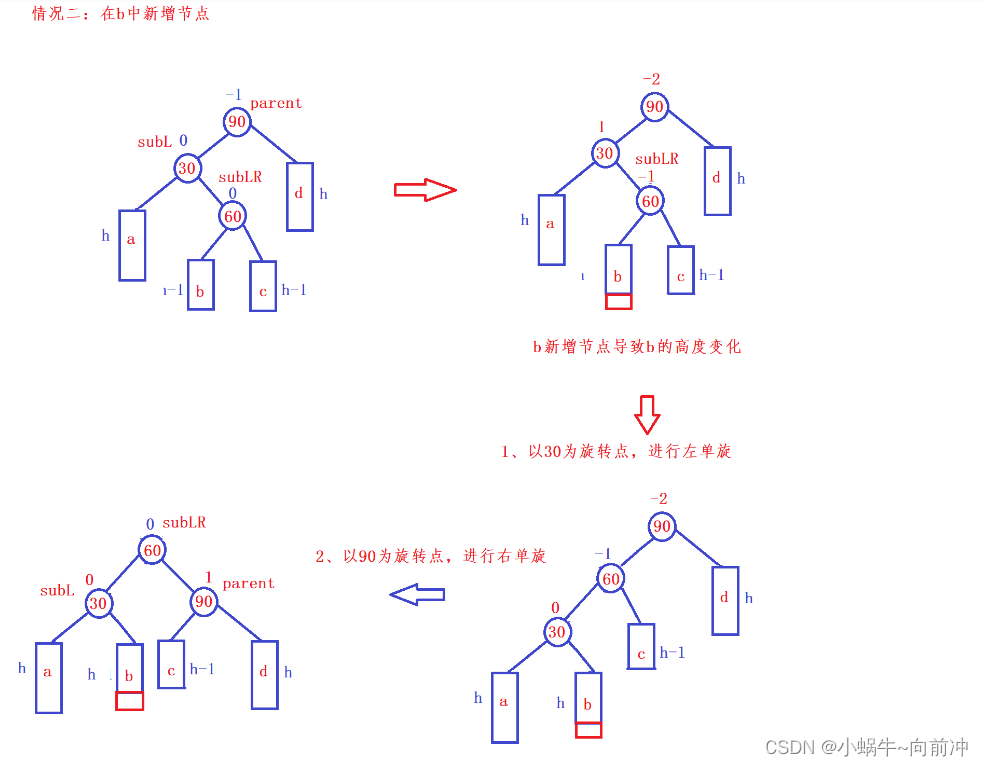
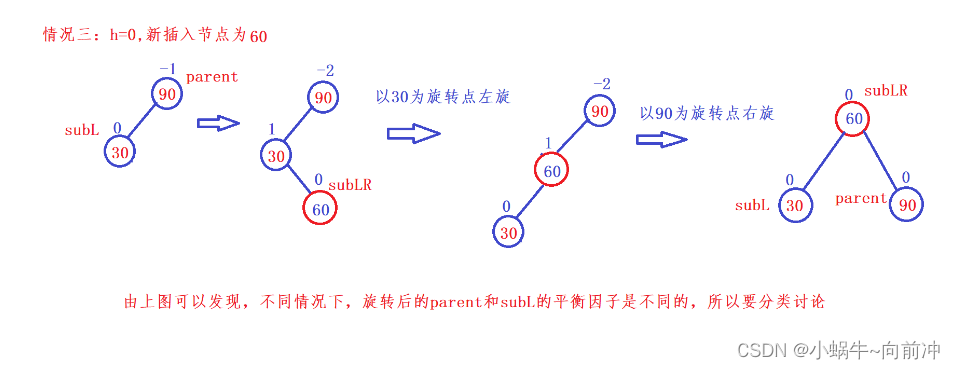
对于双旋转来说，最为重要的平衡因子的更新。 

 代码实现：

//左右双旋
void RotateLR(Node* parent)
{Node* subL = parent->_left;Node* subLR = subL->_right;//记录subLR的平衡因子int bf = subLR->_bf;RotateL(parent->_left);RotateR(parent);//根据不同情况更新平衡因子if (bf == 1)//在c点处新增(在subLR的右子树新增){subLR->_bf = 0;parent->_bf = 0;subL->_bf = -1;}else if(bf == -1) // 在b点处新增(在subLR的左子树新增){subLR->_bf = 0;subL->_bf = 0;parent->_bf = 1;}else if (bf == 0) //自己就是增点{subLR->_bf = 0;parent->_bf = 0;subL->_bf = 0;}else{assert(false);}
}

4、 右左双旋

这里同样也要进行分类讨论：

 

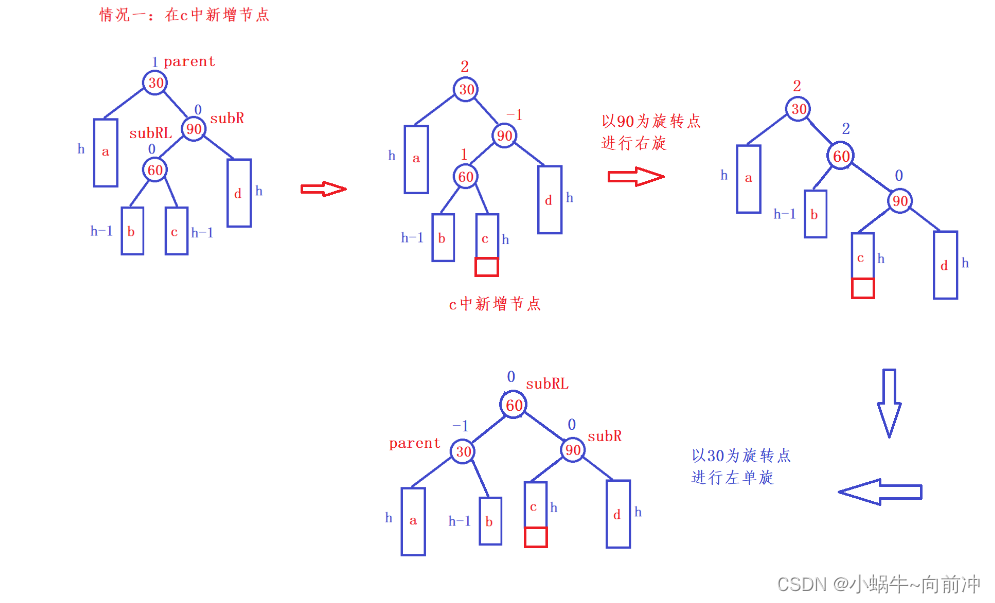
代码实现： 

//右左双旋
void RotateRL(Node* parent)
{Node* subR = parent->_right;Node* subRL = subR->_left;//记录subLR的平衡因子int bf = subRL->_bf;RotateR (parent->_right);RotateL(parent);//根据不同情况更新平衡因子if (bf == 1)//在c点处新增(在subLR的右子树新增){subR->_bf = 0;subRL->_bf = 0;parent->_bf = -1;}else if (bf == -1) // 在b点处新增(在subLR的左子树新增){subR->_bf = 1;subRL->_bf = 0;parent->_bf = 0;}else if (bf == 0) //自己就是增点{subR->_bf = 0;subRL->_bf = 0;parent->_bf = 0;}else{assert(false);}
}

三、AVL树的测试 

为了测试我们模拟实现的AVL树是否成功，还需要进行检查

1、测试的补充代码

树的高度：

int Height()
{return _Height(_root);
}
//求树的高度
int _Height(Node* root)
{//树高度为0if (root == nullptr){return 0;}//递归求左树的高度int Lh = _Height(root->_left);//递归求右树的高度int Rh = _Height(root->_right);return  Lh > Rh ? Lh + 1 : Rh + 1;
}

检查平衡因子

	//检测平衡因子bool _IsBalance(Node* root){if (root == nullptr){return true;}int leftHeight = _Height(root->_left);int rightHeight = _Height(root->_right);if (rightHeight - leftHeight != root->_bf){cout << root->_bf << endl;cout << rightHeight - leftHeight << endl;cout << root->_kv.first << "平衡因子异常" << endl;return false;}return abs(rightHeight - leftHeight) < 2&& _IsBalance(root->_left)&& _IsBalance(root->_right);}

中序遍历

	void InOrder()//这是为了解决在外面调用,不好传根的问题{_InOrder(_root);}//中序遍历void _InOrder(Node* root){if (root == nullptr)return;_InOrder(root->_left);cout << root->_kv.first << ":" << root->_kv.second << endl;_InOrder(root->_right);}

2、测试 

完整代码：

#pragma once
#include<time.h>
#include<assert.h>template<class k,class v>
struct AVLTreeNode
{pair<k, v>_kv;AVLTreeNode<k, v>* _left;AVLTreeNode<k, v>* _right;AVLTreeNode<k, v>* _parent;int _bf;//balance factor//带参数的构造函数AVLTreeNode(const pair<k,v>& kv):_kv(kv),_left(nullptr),_right(nullptr),_parent(nullptr),_bf(0){}
};
template<class k, class v>
struct AVLTree
{typedef AVLTreeNode<k,v> Node;
public://插入bool Insert(const pair<k, v>& kv){if (_root == nullptr){_root = new Node(kv);return true;}Node* parent = nullptr;Node* cur = _root;//找插入位置while (cur){//插入元素大于比较元素if (cur->_kv.first < kv.first){parent = cur;//继续往右树走cur = cur->_right;}else if (cur->_kv.first > kv.first){parent = cur;//继续往左树走cur = cur->_left;}else//插入元素于树中元素相等，不插入{return false;}}cur = new Node(kv);//链接节点if (parent->_kv.first > kv.first){parent->_left = cur;//更新parentcur->_parent = parent;}else{parent->_right = cur;//更新parentcur->_parent = parent;}//更新平衡因子while (parent)//parent为空，就更新到了根{//新增在树节点左边，parent->bf--//新增在树节点右边，parent->bf++if (cur == parent->_left){parent->_bf--;}else{parent->_bf++;}//是否要在更新平衡因子，要根据子树的高度：//1、如果parent->_bf==0,者说明以前的parent->_bf==-1或者parent->_bf==1//即是以前是一边高一边低，现在是插入到矮的一边，树的高度不变，不更新//2、如果parent->_bf==-1或者parent->_bf==-1，者以前parent->_bf==0//即是以前树是均衡的，现在插入让一边高了//子树的高度变了，要向上更新//3 、如果parent->_bf==-2或者parent->_bf==2，者以前parent->_bf==-1或者parent->_bf==1//现在树严重不平衡，让树旋转维持结构//旋转：if (parent->_bf == 0){break;}else if (parent->_bf == -1 || parent->_bf == 1){cur = parent;parent = parent->_parent;}//旋转else if (parent->_bf == -2 || parent->_bf == 2){//左单旋转if (parent->_bf == 2 && cur->_bf == 1){RotateL(parent);}//右单旋else if (parent->_bf == -2 && cur->_bf == -1){RotateR(parent);}//左右双旋else if (parent->_bf == -2 && cur->_bf == 1){RotateLR(parent);}//右左双旋else if (parent->_bf == 2 && cur->_bf == -1){RotateRL(parent);}else{assert(false);}//旋转完成,平衡因子已经更新跳出循环break;}else{assert(false);}}}void RotateL(Node * parent){Node* subR = parent->_right;//父节点的右子树Node* subRL = subR->_left;//右树的左树//让60左边链接到30的右边parent->_right = subRL;if (subRL){subRL->_parent = parent;}Node* ppNode = parent->_parent;//让30变成60的左边subR->_left = parent;parent->_parent = subR;//subR就是根节点if (ppNode == nullptr){_root = subR;_root->_parent = nullptr;}else{//上层父节点的左边是子树的parentif (ppNode->_left == parent){ppNode->_left = subR;}else{ppNode->_right = subR;}//子树父节点和上层父节点链接subR->_parent = ppNode;}//更新平衡因子parent->_bf = subR->_bf = 0;}//右单旋void RotateR(Node* parent){Node* subL = parent->_left;Node* subLR = subL->_right;//b做60的右parent->_left = subLR;if (subLR){subLR->_parent = parent;}Node* ppNode = parent->_parent;//60做30的右subL->_right = parent;parent->_parent = subL;//60就是以前的根节点if (ppNode == nullptr){_root = subL;subL->_parent = ppNode;}else{//上层父节点的左边是子树的parentif (ppNode->_left == parent){ppNode->_left = subL;}else{ppNode->_right = subL;}subL->_parent = ppNode;}//更新平衡因子parent->_bf = subL->_bf = 0;}//左右双旋void RotateLR(Node* parent){Node* subL = parent->_left;Node* subLR = subL->_right;//记录subLR的平衡因子int bf = subLR->_bf;RotateL(parent->_left);RotateR(parent);//根据不同情况更新平衡因子if (bf == 1)//在c点处新增(在subLR的右子树新增){subLR->_bf = 0;parent->_bf = 0;subL->_bf = -1;}else if(bf == -1) // 在b点处新增(在subLR的左子树新增){subLR->_bf = 0;subL->_bf = 0;parent->_bf = 1;}else if (bf == 0) //自己就是增点{subLR->_bf = 0;parent->_bf = 0;subL->_bf = 0;}else{assert(false);}}//右左双旋void RotateRL(Node* parent){Node* subR = parent->_right;Node* subRL = subR->_left;//记录subLR的平衡因子int bf = subRL->_bf;RotateR (parent->_right);RotateL(parent);//根据不同情况更新平衡因子if (bf == 1)//在c点处新增(在subLR的右子树新增){subR->_bf = 0;subRL->_bf = 0;parent->_bf = -1;}else if (bf == -1) // 在b点处新增(在subLR的左子树新增){subR->_bf = 1;subRL->_bf = 0;parent->_bf = 0;}else if (bf == 0) //自己就是增点{subR->_bf = 0;subRL->_bf = 0;parent->_bf = 0;}else{assert(false);}}int Height(){return _Height(_root);}//求树的高度int _Height(Node* root){//树高度为0if (root == nullptr){return 0;}//递归求左树的高度int Lh = _Height(root->_left);//递归求右树的高度int Rh = _Height(root->_right);return  Lh > Rh ? Lh + 1 : Rh + 1;}bool IsAVLTree(){return _IsBalance(_root);}//检测平衡因子bool _IsBalance(Node* root){if (root == nullptr){return true;}int leftHeight = _Height(root->_left);int rightHeight = _Height(root->_right);if (rightHeight - leftHeight != root->_bf){cout << root->_bf << endl;cout << rightHeight - leftHeight << endl;cout << root->_kv.first << "平衡因子异常" << endl;return false;}return abs(rightHeight - leftHeight) < 2&& _IsBalance(root->_left)&& _IsBalance(root->_right);}void InOrder()//这是为了解决在外面调用,不好传根的问题{_InOrder(_root);}//中序遍历void _InOrder(Node* root){if (root == nullptr)return;_InOrder(root->_left);cout << root->_kv.first << ":" << root->_kv.second << endl;_InOrder(root->_right);}private:Node* _root = nullptr;
};void TestAVLTree1()
{//int a[] = { 8, 3, 1, 10, 6, 4, 7, 14, 13 };//int a[] = { 16, 3, 7, 11, 9, 26, 18, 14, 15 };/*int a[] = { 4, 2, 6, 1, 3, 5, 15, 7, 16, 14 };*/int a[] = { 30,60,90 };AVLTree<int, int> t;for (auto e : a){t.Insert(make_pair(e, e));}t.InOrder();cout << t.IsAVLTree() << endl;
}
void TestAVLTree2()
{srand(time(0));const size_t N = 100000;AVLTree<int, int> t;for (size_t i = 0; i < N; ++i){size_t x = rand();t.Insert(make_pair(x, x));/*cout << t.IsAVLTree() << endl;*/}cout << t.IsAVLTree() << endl;
}

这里我们分别进行简单 TestAVLTree1()和用生成随机数字生成的数字进行测试TestAVLTree2()

如果成功就会打印1.