rotation matrix reflection matrix
文章目录
- 1. rotation matrix
- 1.1 结论
- 2. reflection matrix
- 2.1 结论
1. rotation matrix
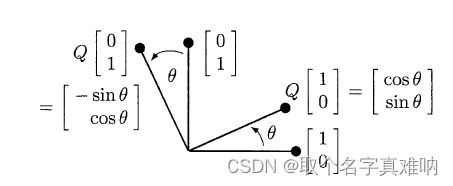
图像逆时针旋转 θ \theta θ的矩阵
Q r o t a t e = [ cos θ − sin θ sin θ cos θ ] (1) Q_{rotate}=\begin{bmatrix}\cos\theta&-\sin\theta\\\sin\theta&\cos\theta\end{bmatrix}\tag1 Qrotate=[cosθsinθ−sinθcosθ](1)
- 为了方便计算和表达,我们用 I I I单位矩阵进行分析
I = [ 1 0 0 1 ] (2) I=\begin{bmatrix}1&0\\0&1\end{bmatrix}\tag2 I=[1001](2)
可以得到两个点 Q=(1 , 0);Q=( 0, 1),我们将两个向量逆时针旋转 θ \theta θ角度后,可以得到此时的角度
Q ′ [ 1 , 0 ] = [ cos θ sin θ ] (3) Q'[1,0]=\begin{bmatrix}\cos\theta\\\sin\theta\end{bmatrix}\tag3 Q′[1,0]=[cosθsinθ](3)
Q ′ [ 0 , 1 ] = [ − sin θ cos θ ] (4) Q'[0,1]=\begin{bmatrix}-\sin\theta\\\cos\theta\end{bmatrix}\tag4 Q′[0,1]=[−sinθcosθ](4)
所以可以得到 I I I单位向量在逆时针旋转 θ \theta θ后的旋转矩阵如下
1.1 结论
Q r o t a t e = [ cos θ − sin θ sin θ cos θ ] (5) Q_{rotate}=\begin{bmatrix}\cos\theta&-\sin\theta\\\sin\theta&\cos\theta\end{bmatrix}\tag5 Qrotate=[cosθsinθ−sinθcosθ](5)
2. reflection matrix
Q r o t a t e = [ cos θ − sin θ sin θ cos θ ] (6) Q_{rotate}=\begin{bmatrix}\cos\theta&-\sin\theta\\\sin\theta&\cos\theta\end{bmatrix}\tag6 Qrotate=[cosθsinθ−sinθcosθ](6)
图像沿着直线 1 2 θ \frac{1}{2}\theta 21θ对称矩阵,反射矩阵
- 为了方便计算和表达,我们用 I I I单位矩阵进行分析
I = [ 1 0 0 1 ] (7) I=\begin{bmatrix}1&0\\0&1\end{bmatrix}\tag7 I=[1001](7)
可以得到两个点 Q=(1 , 0);Q=( 0, 1),我们将两个向量关于 1 2 θ \frac{1}{2}\theta 21θ直线对称后,可以得到此时的坐标
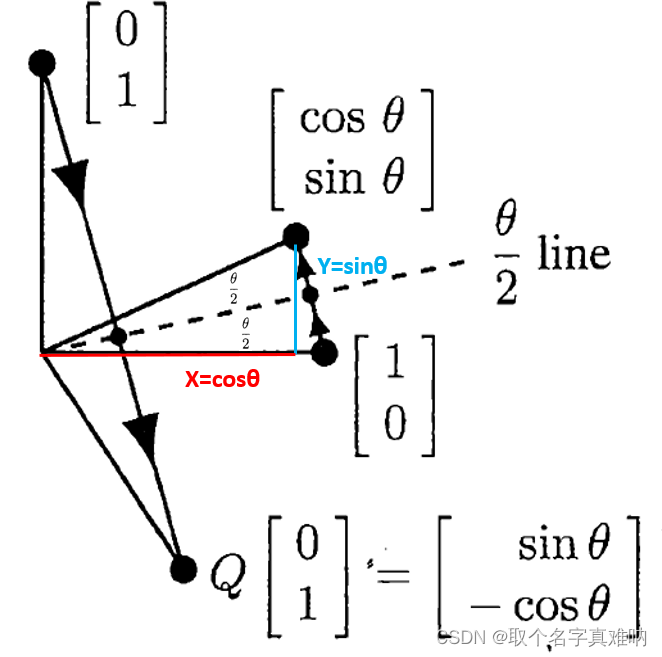
Q ′ [ 1 , 0 ] = [ cos θ sin θ ] (8) Q'[1,0]=\begin{bmatrix}\cos\theta\\\sin\theta\end{bmatrix}\tag8 Q′[1,0]=[cosθsinθ](8)
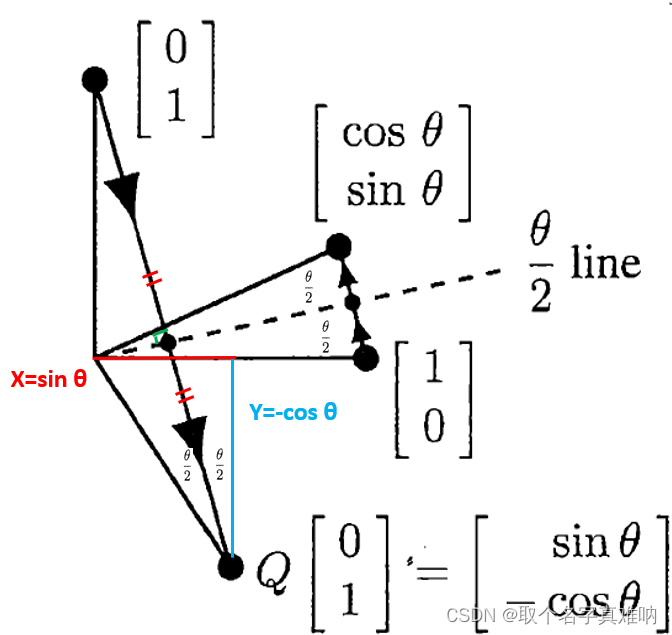
Q ′ [ 0 , 1 ] = [ sin θ − cos θ ] (9) Q'[0,1]=\begin{bmatrix}\sin\theta\\-\cos\theta\end{bmatrix}\tag9 Q′[0,1]=[sinθ−cosθ](9)
2.1 结论
Q r e f l e c t i o n = [ cos θ sin θ sin θ − cos θ ] (10) Q_{reflection}=\begin{bmatrix}\cos\theta&\sin\theta\\\sin\theta&-\cos\theta\end{bmatrix}\tag{10} Qreflection=[cosθsinθsinθ−cosθ](10)
相关文章:

rotation matrix reflection matrix
文章目录 1. rotation matrix1.1 结论 2. reflection matrix2.1 结论 1. rotation matrix 图像逆时针旋转 θ \theta θ的矩阵 Q r o t a t e [ cos θ − sin θ sin θ cos θ ] (1) Q_{rotate}\begin{bmatrix}\cos\theta&-\sin\theta\\\sin\theta&\c…...

Python基础教程: sorted 函数
嗨喽,大家好呀~这里是爱看美女的茜茜呐 sorted 可以对所有可迭代的对象进行排序操作, sorted 方法返回的是一个新的 list,而不是在原来的基础上进行的操作。 从新排序列表。 👇 👇 👇 更多精彩机密、教程…...
Vue 重写push和replace方法,解决:Avoided redundant navigation to current location
当我们使用编程式路由导航跳转路径时,如果我们两次携带同样的参数进行跳转,会进行页面报错: 那产生这个问题的原因是什么呢? 我们接收并输出调用push方法返回的结果: 会发现这是一个Promise对象 我们都知道ÿ…...

43、vue导出pdf文件,并解决滚动条外内容无法获取的问题
使用插件html2canvas和jspdf插件 下载完两个插件后引入所需要的页面 import html2canvas from "html2canvas" import jsPDF from "jspdf"1、在导出之前将元素的高度或者宽度设置为滚动高度或者宽度,如: el.style.height el.scro…...
牛客 最小公配数 golang版实现
题目请参考: HJ108 求最小公倍数 题解: 在大的数的倍数里面去找最小的能整除另外一个数的数,就是最小公倍数,按照大的来找,循环次数能够降到很少,提升效率 golang实现: package mainimport ("fmt" )func main() {a : …...
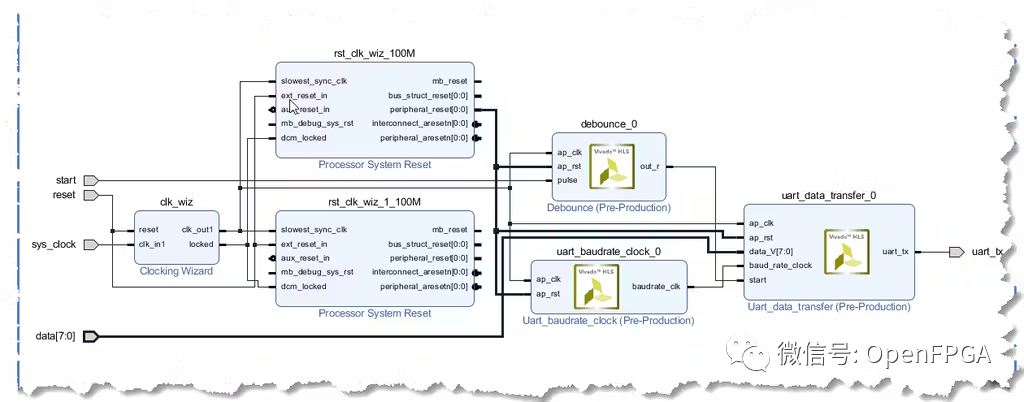
用 HLS 实现 UART
用 HLS 实现 UART 介绍 UART 是一种旧的串行通信机制,但仍在很多平台中使用。它在 HDL 语言中的实现并不棘手,可以被视为本科生的作业。在这里,我将通过这个例子来展示在 HLS 中实现它是多么容易和有趣。 因此,从概念上讲…...

华清远见嵌入式学习——网络编程——作业4
作业要求:①使用IO多路复用中的select函数实现TCP并发服务器客户端 ②使用IO多路复用中的poll函数实现TCP并发服务器的服务器端 一、 代码 #include <myhead.h>#define SERPORT 8888 //服务器端口号 #define SERIP "192.168.114.113"…...
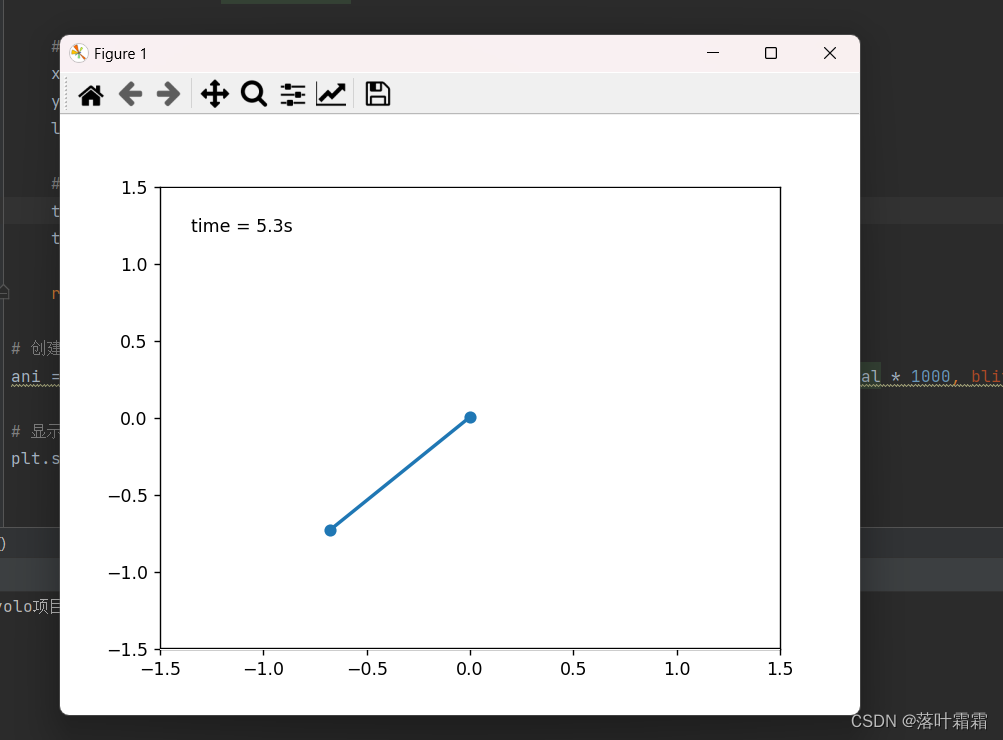
【OpenCV实现图像:制作酷炫的动画效果】
文章目录 概要生成背景图添加点动画添加文本显示小结 概要 首先,通过导入必要的库,包括NumPy用于数学运算和Matplotlib库用于数据可视化。随后,创建图形和轴,初始化点的位置,以及编写初始化函数和更新函数。 初始化函…...

CSS鼠标属性篇
属性名:cursor 功能:设置鼠标光标的样式 属性值: pointer:小手move:移动图标text:文字选择器crosshair:十字架wait:等待help:帮助 eg.html{ cursor: wait;}(此处使用css改…...

交直流一体化电源系统测试步骤详解
交直流一体化电源拥有高度适应性,可以用于不同的电力需求领域。但是为了确保其质量和性能,需要对交直流一体化电源进行各项测试以保证正常工作。本文纳米软件将介绍交直流一体化电源的测试方法,以及如何用交直流一体化电源测试系统进行测试。…...

多数据库使用django-apscheduler时,migrate后并不能生成django_apscheduler_djangojob表的问题
先说一下django-apscheduler定时器的使用过程: django-apscheduler基本使用 1.安装django-apscheduler代码如下(示例): pip install django-apscheduler 2.配置settings.py的INSTALLED_APPS代码如下(示例)…...
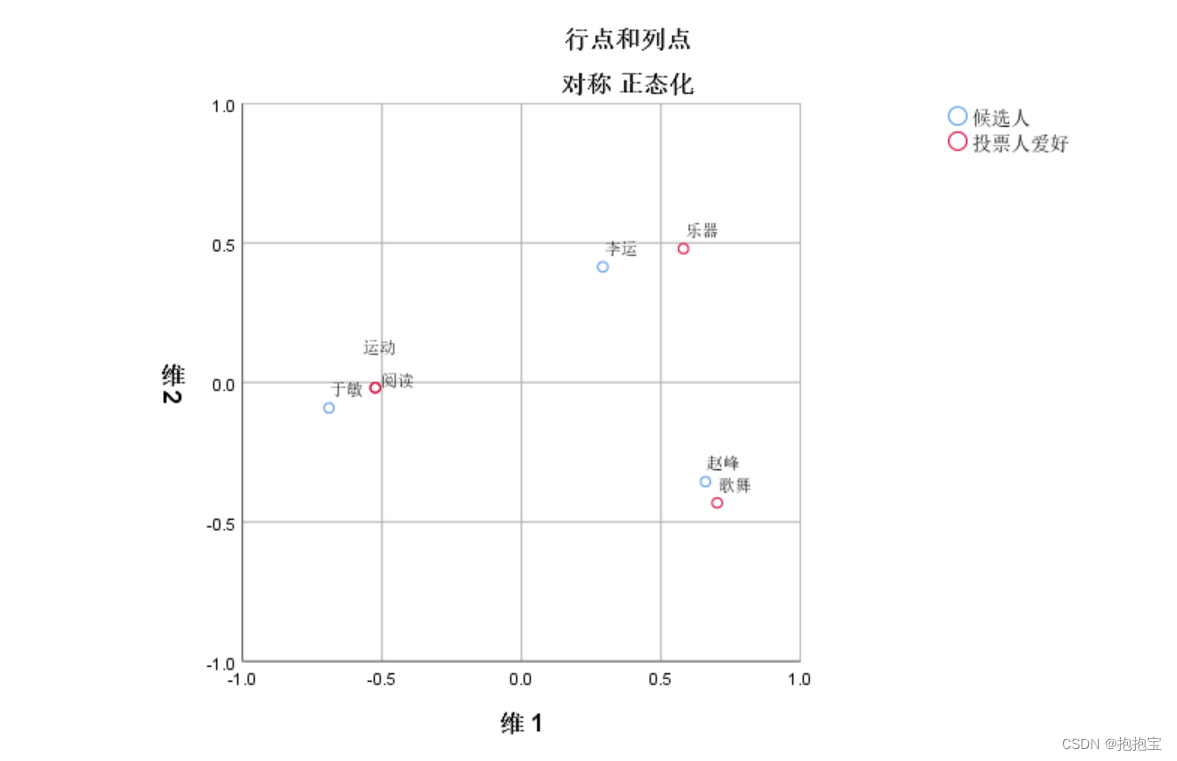
SPS简单对应分析
前言: 本专栏参考教材为《SPSS22.0从入门到精通》,由于软件版本原因,部分内容有所改变,为适应软件版本的变化,特此创作此专栏便于大家学习。本专栏使用软件为:SPSS25.0 本专栏所有的数据文件请点击此链接下…...

智能井盖传感器建设信息化时代智慧城市
近年来随着信息技术的快速发展和城市化进程的加速推进,智慧城市的概念逐渐成为现实。作为智慧城市生命线建设中的重要组成部分,智能井盖传感器的应用正在为城市的可持续发展和居民的生活质量提供新的解决方案。 智能井盖传感器能够实时监测井盖状态&…...
安装向量数据库milvus及其Attu
前置条件安装docker compose 在宿主机上创建文件目录 mkdir -p /home/sunyuhua/milvus/db mkdir -p /home/sunyuhua/milvus/conf mkdir -p /home/sunyuhua/milvus/etcd下载docker-compose.yml wget https://github.com/milvus-io/milvus/releases/download/v2.2.11/milvus-s…...

量子计算概述
目录 1.量子计算介绍 2.量子计算应用 3.量子计算研究机构 1.量子计算介绍 量子计算是一种遵循量子力学规律调控量子信息单元进行计算的新型计算模式。经典计算使用2进制进行运算,但2进制只有0和1两种状态,而量子计算除了包含0和1两种状…...
校园圈子论坛,交友,帖子内短视频,二手市场,APP小程序H5三端交付,源码交付,支持二开
校园圈子论坛,交友频道,商城,二手市场,活动专区,短视频,从校园生活的方方面面展现出了充满活力和创造力的镜头。这个频道是一个让学生们相互交流、结识新朋友的平台,不仅有交友功能,…...

Request 爬虫的 SSL 连接问题深度解析
SSL 连接简介 SSL(Secure Sockets Layer)是一种用于确保网络通信安全性的加密协议,广泛应用于互联网上的数据传输。在数据爬取过程中,爬虫需要与使用 HTTPS 协议的网站进行通信,这就牵涉到了 SSL 连接。本文将深入研究…...
gin相关操作--一起学习921190764
gin官方文档 https://gin-gonic.com/docs/quickstart/1. 安装 go get -u github.com/gin-gonic/ginhttps://github.com/gin-gonic/gin简单入门 package mainimport ("github.com/gin-gonic/gin""net/http" )func pong(c *gin.Context) {//c.JSON(http.S…...

Linux查看开机启动的服务
在Linux系统中,可以使用不同的命令和工具来查看开机启动的服务。以下是一些常用的方法: systemctl 命令: 使用 systemctl 命令可以查看系统中所有正在运行的服务以及它们的状态。 systemctl list-units --typeservice若要查看某个特定服务的…...
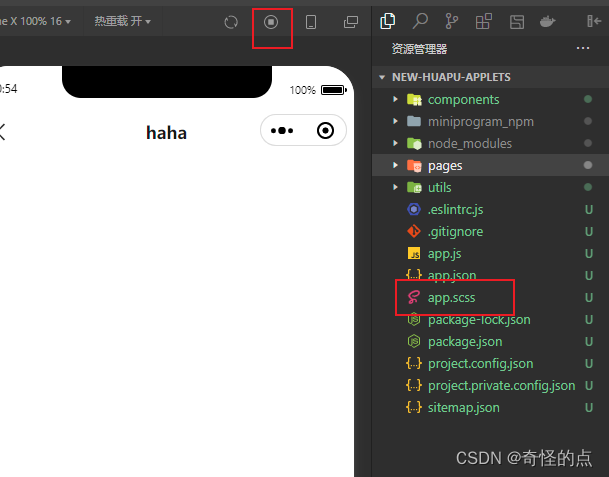
微信小程序如何使用scss,less
搜到很多都是先VSCode安装好…插件…。这都是很久之前的方法了,所以想写这篇文章 一、修改project.config.json配置文件 "setting": {"useCompilerPlugins": ["sass"]},二、然后就可以删除 .wxss 文件了,就用 .scss 文件…...

css实现圆环展示百分比,根据值动态展示所占比例
代码如下 <view class""><view class"circle-chart"><view v-if"!!num" class"pie-item" :style"{background: conic-gradient(var(--one-color) 0%,#E9E6F1 ${num}%),}"></view><view v-else …...

C++:std::is_convertible
C++标志库中提供is_convertible,可以测试一种类型是否可以转换为另一只类型: template <class From, class To> struct is_convertible; 使用举例: #include <iostream> #include <string>using namespace std;struct A { }; struct B : A { };int main…...

模型参数、模型存储精度、参数与显存
模型参数量衡量单位 M:百万(Million) B:十亿(Billion) 1 B 1000 M 1B 1000M 1B1000M 参数存储精度 模型参数是固定的,但是一个参数所表示多少字节不一定,需要看这个参数以什么…...

Neo4j 集群管理:原理、技术与最佳实践深度解析
Neo4j 的集群技术是其企业级高可用性、可扩展性和容错能力的核心。通过深入分析官方文档,本文将系统阐述其集群管理的核心原理、关键技术、实用技巧和行业最佳实践。 Neo4j 的 Causal Clustering 架构提供了一个强大而灵活的基石,用于构建高可用、可扩展且一致的图数据库服务…...

关于 WASM:1. WASM 基础原理
一、WASM 简介 1.1 WebAssembly 是什么? WebAssembly(WASM) 是一种能在现代浏览器中高效运行的二进制指令格式,它不是传统的编程语言,而是一种 低级字节码格式,可由高级语言(如 C、C、Rust&am…...

让回归模型不再被异常值“带跑偏“,MSE和Cauchy损失函数在噪声数据环境下的实战对比
在机器学习的回归分析中,损失函数的选择对模型性能具有决定性影响。均方误差(MSE)作为经典的损失函数,在处理干净数据时表现优异,但在面对包含异常值的噪声数据时,其对大误差的二次惩罚机制往往导致模型参数…...

android13 app的触摸问题定位分析流程
一、知识点 一般来说,触摸问题都是app层面出问题,我们可以在ViewRootImpl.java添加log的方式定位;如果是touchableRegion的计算问题,就会相对比较麻烦了,需要通过adb shell dumpsys input > input.log指令,且通过打印堆栈的方式,逐步定位问题,并找到修改方案。 问题…...

Spring AI Chat Memory 实战指南:Local 与 JDBC 存储集成
一个面向 Java 开发者的 Sring-Ai 示例工程项目,该项目是一个 Spring AI 快速入门的样例工程项目,旨在通过一些小的案例展示 Spring AI 框架的核心功能和使用方法。 项目采用模块化设计,每个模块都专注于特定的功能领域,便于学习和…...

【实施指南】Android客户端HTTPS双向认证实施指南
🔐 一、所需准备材料 证书文件(6类核心文件) 类型 格式 作用 Android端要求 CA根证书 .crt/.pem 验证服务器/客户端证书合法性 需预置到Android信任库 服务器证书 .crt 服务器身份证明 客户端需持有以验证服务器 客户端证书 .crt 客户端身份…...

聚六亚甲基单胍盐酸盐市场深度解析:现状、挑战与机遇
根据 QYResearch 发布的市场报告显示,全球市场规模预计在 2031 年达到 9848 万美元,2025 - 2031 年期间年复合增长率(CAGR)为 3.7%。在竞争格局上,市场集中度较高,2024 年全球前十强厂商占据约 74.0% 的市场…...
