【视觉SLAM十四讲学习笔记】第三讲——旋转矩阵
专栏系列文章如下:
【视觉SLAM十四讲学习笔记】第一讲——SLAM介绍
【视觉SLAM十四讲学习笔记】第二讲——初识SLAM
本章将介绍视觉SLAM的基本问题之一:如何描述刚体在三维空间中的运动?
旋转矩阵
点、向量和坐标系
三维空间由3个轴组成,所以一个空间点的位置可以由3个坐标指定。而刚体,它不光有位置,还有自身的姿态。举个例子,相机也可以看成三维空间的刚体,于是位置是指相机在空间中的哪个地方,而姿态则是指相机的朝向,合起来称为位姿。
点: 点是空间中的基本元素,没有长度,没有体积。
向量: 把两个点连接起来,就构成了向量。向量可以看成从某点指向另一点的一个箭头。不要把向量与它的坐标两个概念混淆。一个向量是空间当中的一样东西,并不需要和若干个实数相关联的。只有当我们指定这个三维空间中的某个坐标系时,才可以谈论该向量在此坐标系下的坐标,也就是找到若干个实数对应这个向量。简单来讲:向量本身就是一个东西,如果把它放在一个坐标系中,这个向量才有了对应于这个坐标系的坐标。
用线性代数的知识来说,三维空间中的某个点的坐标也可以用线性空间R^3来描述。假设在这个线性空间内,有该空间的一组基 (或者说基底)(e1,e2,e3),(基就是张成这个空间的一组线性相关的向量)那么,任意向量a在这组基下就有一个坐标,这里 (a1,a2,a3)T 称为a在此基下的坐标。公式如下:
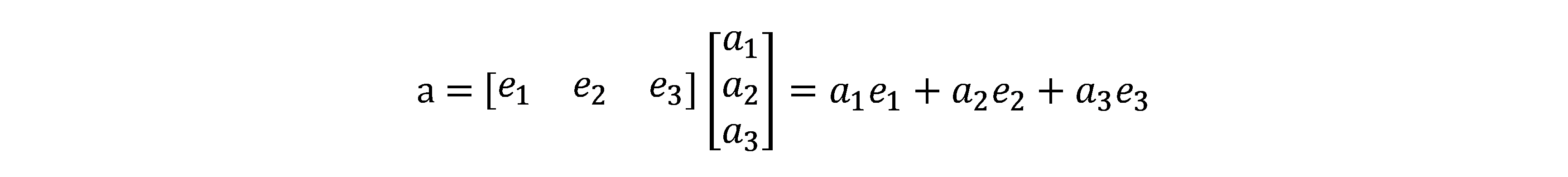
坐标的具体取值,一是和向量本身有关,二是和坐标系(基)的选取有关。坐标系通常由3个正交的坐标轴组成,非正交的很少见。通常使用右手系,给定x和y轴时,z 轴就可以通过右手法则由x × y定义出来。左手系的第3个轴与右手系的方向相反。
向量内积: 可以描述向量间的投影关系
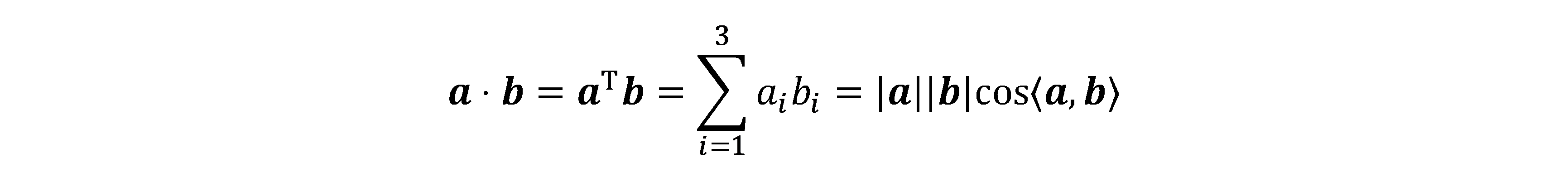
其中<a,b>指向量a,b的夹角。
向量外积:
外积的结果是一个向量,它的方向垂直于这两个向量,大小为 |a||b|sin〈a,b〉,是两个向量张成的四边形的有向面积。
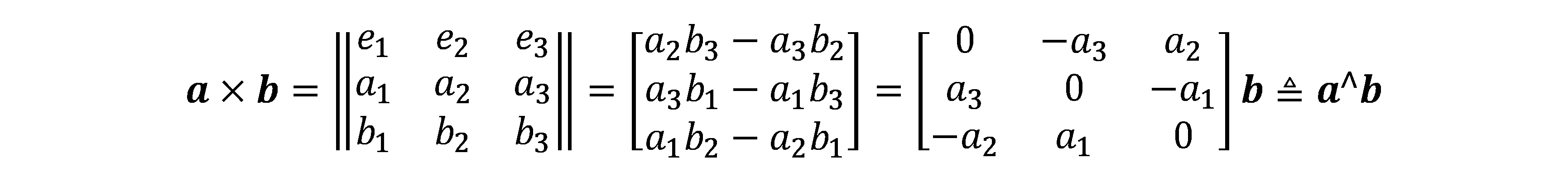
对于外积运算,我们引入∧符号,把a写成一个矩阵,事实上是一个反对称矩阵(Skew-symmetric matrix),反对称矩阵A满足AT = -A。你可以将∧记成一个反对称符号。这样就把外积a × b写成了矩阵与向量的乘法a∧b,把它变成了线性运算。这意味着任意向量都对应着唯一的一个反对称矩阵,反之亦然:
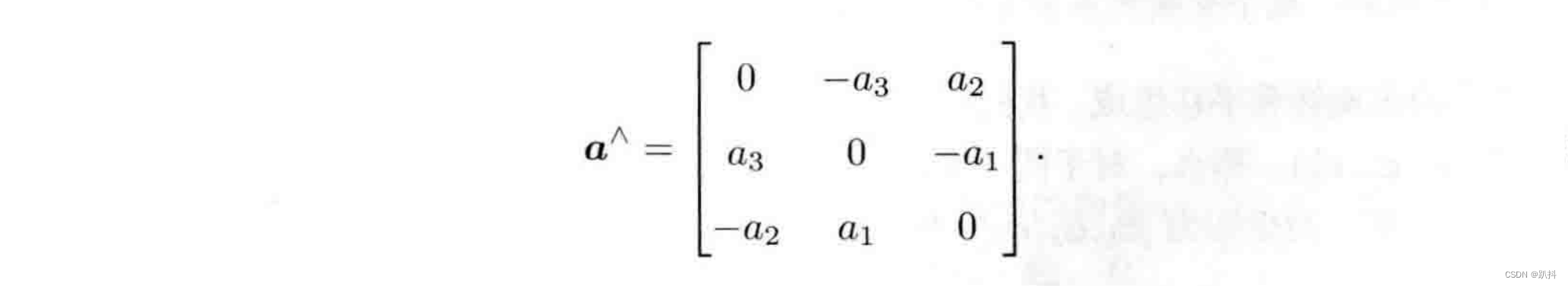
向量和加减法、内外积,即使在不谈论它们的坐标时也可以计算。例如,虽然内积在有坐标时,可以用两个向量的分量乘积之和表达,但是即使不知道它们的坐标时,也可以通过长度和夹角来计算二者的内积。所以两个向量的内积结果和坐标系的选取是无关的。
坐标系间的欧式变换
考虑运动的机器人,常见的做法是设定一个惯性坐标系(或者叫世界坐标系),可以认为它是固定不动的。相机或机器人则是一个移动坐标系。相机视野中某个向量p,它在相机坐标系下的坐标为pc,而在世界坐标系下看,它的坐标为pw。如果要实现这两个坐标之间的转换,需要先得到该点针对机器人坐标系的坐标值,再根据机器人位姿变换到世界坐标系中。我们需要一种数学手段来描述这个变换关系。
两个坐标系之间的运动由一个旋转加上一个平移组成,这种运动称为刚体运动。相机运动就是一个刚体运动。刚体运动过程中,同一个向量在各个坐标系下的长度和夹角都不会发生变化,只可能有空间位置和姿态的不同。此时,我们说刚体坐标系到世界坐标之间,相差了一个欧氏变换(Euclidean Transform)。
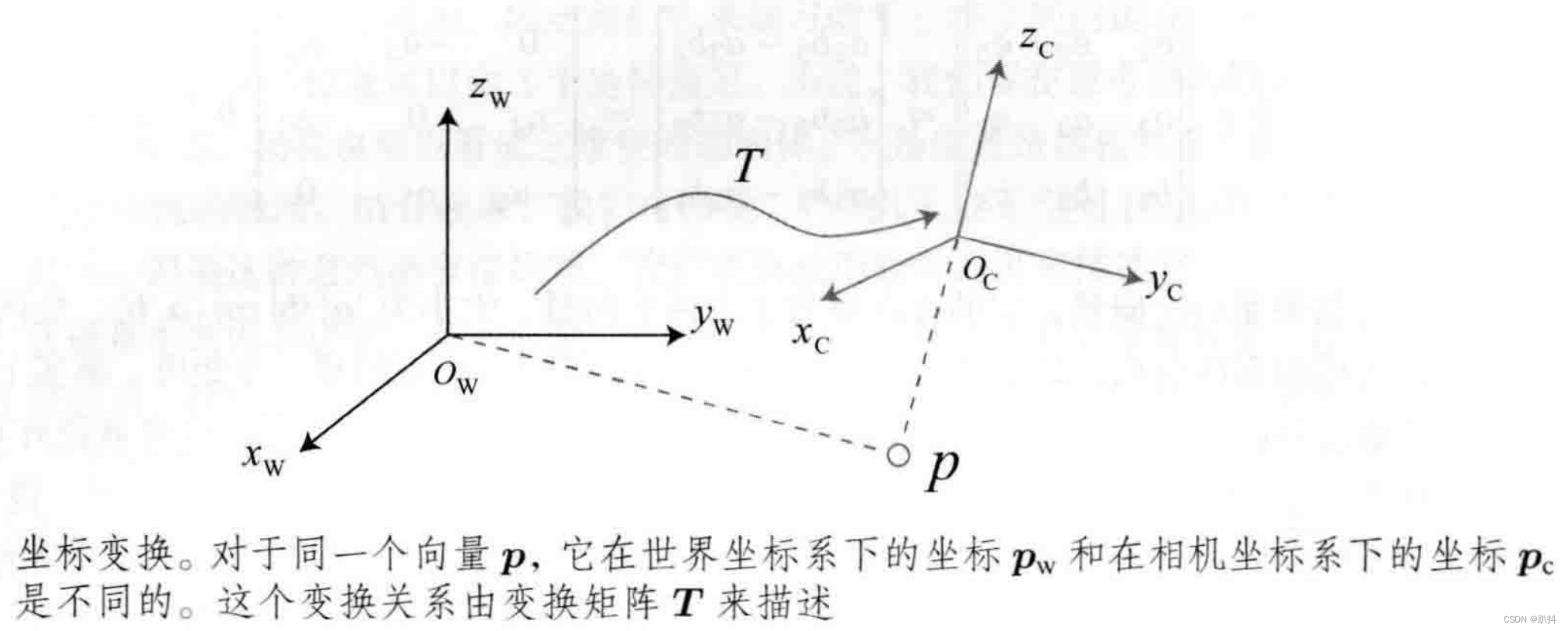
欧氏变换由旋转和平移组成。首先考虑旋转,设某个单位正交基 (e1, e2, e3) 经过一次旋转变成了 (e1’, e2’, e3’) ,那么,对于同一个向量 a(该向量并没有随着坐标系的旋转而发生运动),它在两个坐标系下的坐标为[a1, a2, a3]T和[a1’, a2’, a3’]T。因为向量本身没变,根据坐标的定义,有:
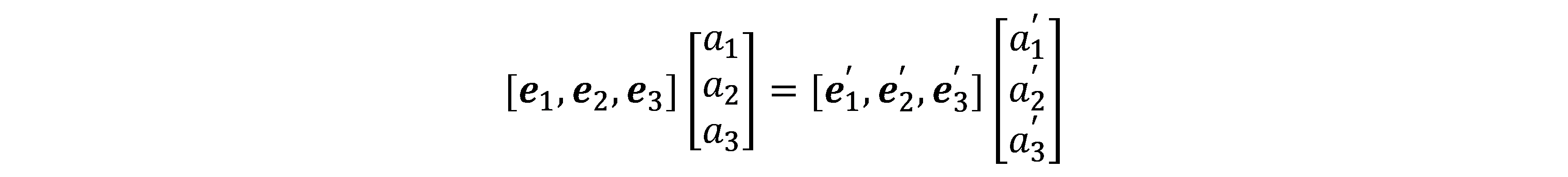
为了描述两个坐标之间的关系,我们对上述等式的左右两边同时左乘
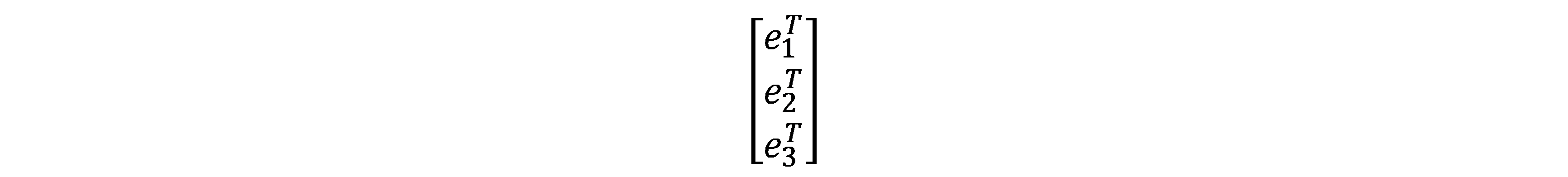
那么左边的系数就变成了单位矩阵,把中间的矩阵拿出来,定义成一个矩阵R:
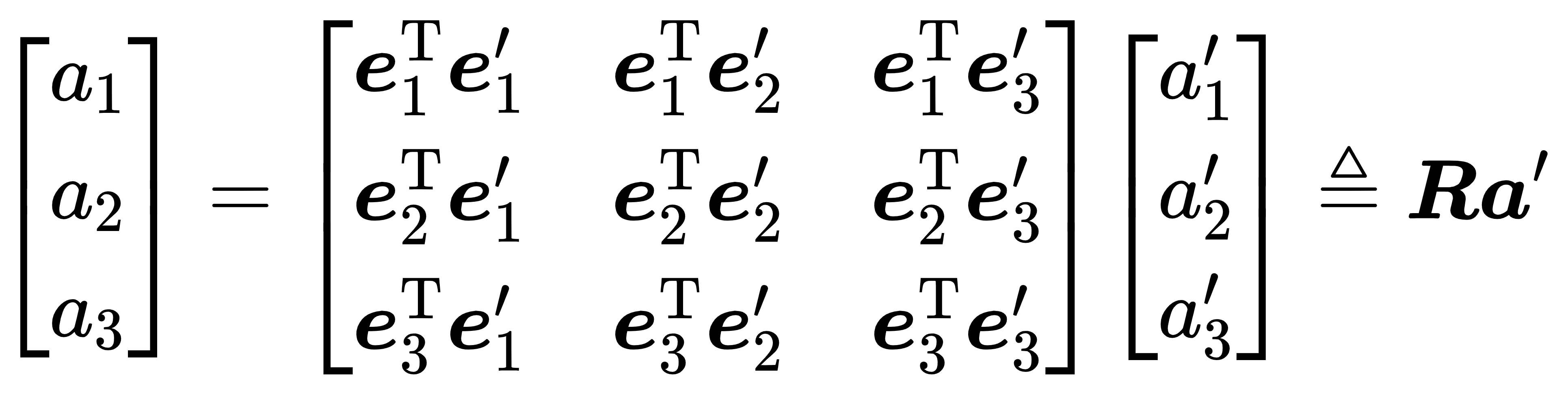
这个矩阵由两组基之间的内积组成,刻画了旋转前后同一个向量的坐标变换关系。只要旋转是一样的,那么这个矩阵也是一样的。可以说,矩阵R描述了旋转本身。因此称为旋转矩阵(Rotation matrix)。该矩阵各分量是两个坐标系基的内积,由于基向量的长度为1,所以实际上是各基向量的夹角之余弦。所以这个矩阵也叫方向余弦矩阵(Direction Cosine matrix)。
旋转矩阵有一些特别的性质。它是一个行列式为1的正交矩阵。反之,行列式为1的正交矩阵也是一个旋转矩阵。以把 n 维旋转矩阵的集合定义如下:
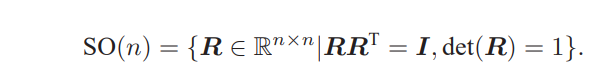
SO(n) 是特殊正交群(Special Orthogonal Group)的意思。这个集合由n维空间的旋转矩阵组成,特别地,SO(3) 就是指三维空间的旋转。通过旋转矩阵,我们可以直接谈论两个坐标系之间的旋转变换,而不用再从基开始谈起。
由于旋转矩阵为正交矩阵,它的逆(即转置)描述了一个相反的旋转:
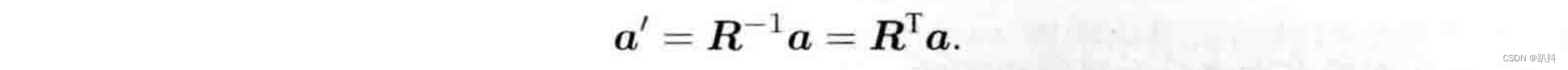
在欧氏变换中,除了旋转之外还有平移。考虑世界坐标系中的向量a,经过一次旋转(用R描述)和一次平移t后,得到了a′,把旋转和平移合到一起,有:
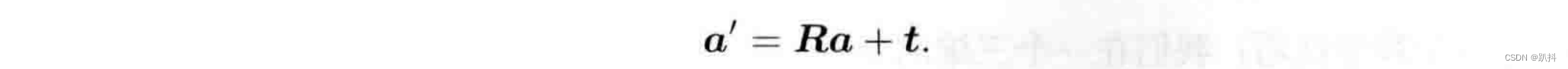
t称为平移向量。平移部分只需把平移向量加到旋转之后的坐标上。
通过上式,我们用一个旋转矩阵R和一个平移向量t完整地描述了一个欧氏空间的坐标变换关系。定义坐标系1、坐标系2,那么向量a在两个系下坐标为 a1, a2,它们之间的关系应该是:
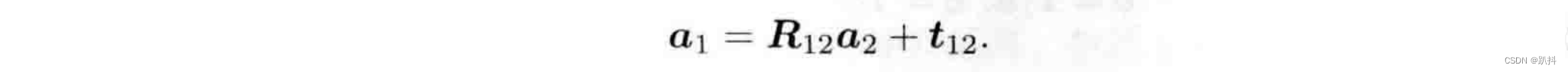
R12 是指把坐标系2的向量变换到坐标系1中。同理,如果我们要表达从1到2的旋转矩阵时,就写成R21。关于平移t12,实际对应的是坐标系1原点指向坐标系2原点的向量,在坐标系1下取的坐标,把它记作从1到2的向量。但是反过来的t21,即从2指向1的向量在坐标系2下的坐标,并不等于−t12,这里和两个系的旋转还有关系。从向量层面来看,它们确实是反向的关系,但这两个向量的坐标值并不是相反数。
变换矩阵与齐次坐标
上面的变换关系并非一个线性关系,一旦变换多次就会非常繁杂。所以我们引入齐次坐标和变换矩阵:
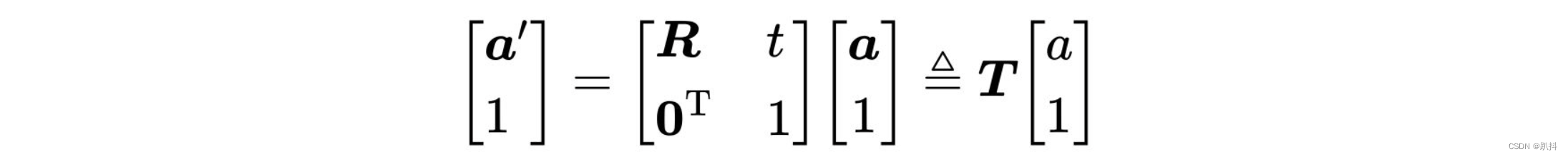
这是一个数学技巧:我们在一个三维向量的末尾添加 1,将其变成了四维向量,称为齐次坐标。对于这个四维向量,我们可以把旋转和平移写在一个矩阵里面,使得整个关系变成线性关系。该式中,矩阵T称为变换矩阵(Transform Matrix)。
我们暂时用ã表示a的齐次坐标。那么依靠齐次坐标和变换矩阵,两次变换的叠加就可以有很好的形式:
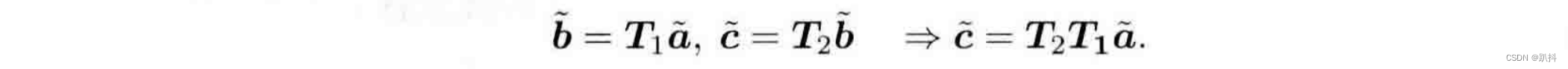
但是懒得区分齐次和非齐次的符号了,所以在不引起歧义的情况下,我们就直接把它写成b=Ta的样子,默认其中进行了齐次坐标的转换。要注意的是,不进行齐次坐标转换时,这边的乘法在矩阵维度上是不成立的。
变换矩阵T具有比较特别的结构:左上角为旋转矩阵,右侧为平移向量,左下角为0 向量,右下角为 1。这种矩阵又称为特殊欧氏群(Special Euclidean Group):
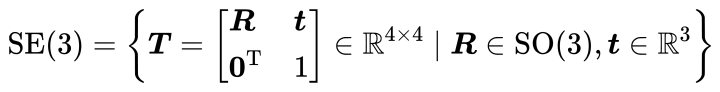
与 SO(3) 一样,求解该矩阵的逆表示一个反向的变换:
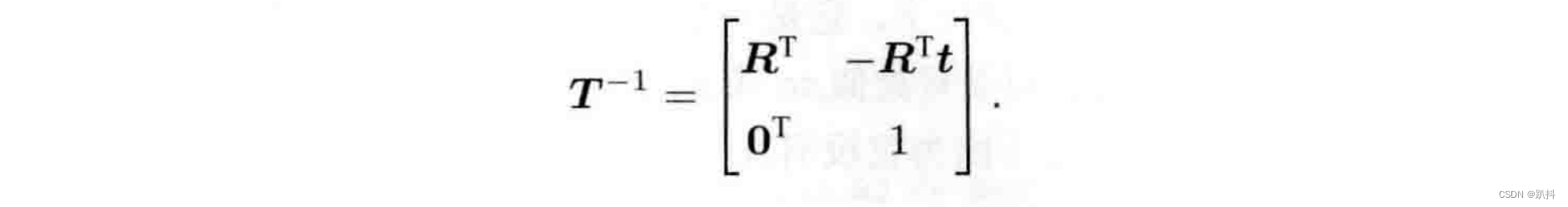
同样,我们用T12 这样的写法来表示从2到1的变换。
总结:
首先介绍了向量及其坐标表示,并介绍了向量间的运算;然后,坐标系之间的运动由欧氏变换描述,它由平移和旋转组成。旋转可以由旋转矩阵 SO(3) 描述,而平移直接由一个R^3向量描述。最后,如果将平移和旋转放在一个矩阵中,就形成了变换矩阵 SE(3)。
相关文章:
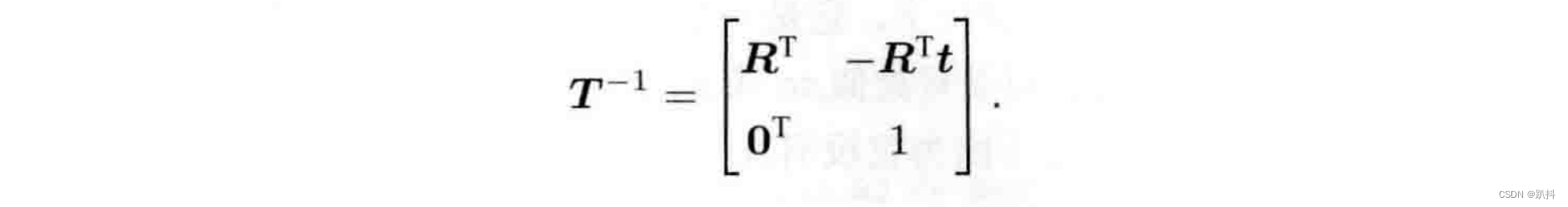
【视觉SLAM十四讲学习笔记】第三讲——旋转矩阵
专栏系列文章如下: 【视觉SLAM十四讲学习笔记】第一讲——SLAM介绍 【视觉SLAM十四讲学习笔记】第二讲——初识SLAM 本章将介绍视觉SLAM的基本问题之一:如何描述刚体在三维空间中的运动? 旋转矩阵 点、向量和坐标系 三维空间由3个轴组成&…...
Linux驱动开发笔记(四):设备驱动介绍、熟悉杂项设备驱动和ubuntu开发杂项设备Demo
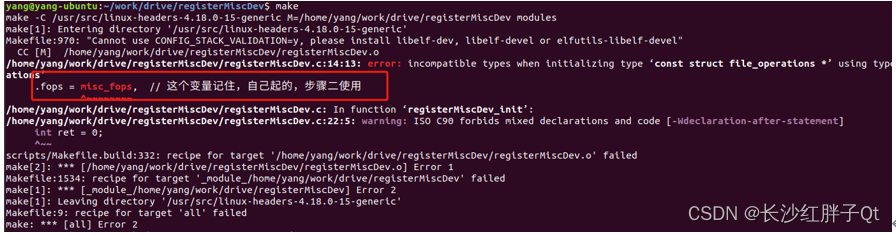
若该文为原创文章,转载请注明原文出处 本文章博客地址:https://hpzwl.blog.csdn.net/article/details/134533533 红胖子网络科技博文大全:开发技术集合(包含Qt实用技术、树莓派、三维、OpenCV、OpenGL、ffmpeg、OSG、单片机、软硬…...

C/C++ 实现Windows注册表操作
Windows注册表(Registry)是Windows操作系统中用于存储系统配置信息、用户设置和应用程序数据的一个集中式数据库。它是一个层次结构的数据库,由键(Key)和值(Value)组成,这些键和值被…...

nginx 模块相关配置及结构理解
文章目录 模块配置结构模块配置指令先看一下 ngx_command_t 结构一个模块配置的demo简单模块配置的案例演示 模块上下文结构模块的定义 模块配置结构 Nginx中每个模块都会提供一些指令,以便于用户通过配置去控制该模块的行为。 Nginx的配置信息分成了几个作用域(sc…...
))
同时创建多个websoket(初始化多个连接、断开的重连、每个连接定时发消息、每个连接存储接收的数据(vuex或者pinia))
可复制现成代码直接使用!! 1.下边的例子演示了创建10个WebSocket 实例,当其中某一个连接失败时,会自动进行重连 <template><div></div> </template><script setup> import { ref, reactive, onMo…...
C语言——指针(一)
📝前言 这篇文章主要带大家初步认识一下指针,供大家理解参考。 主要归纳与讲解: 1,指针与指针变量 2,指针的基本使用(如何定义,初始化,引用) 🎬个人简介&…...

学习量化交易如何入门?
Python 量化入门很简单,只需 3 步就能快速上手! 题主在程序方向没有相关经验,今天就从量化行业的通用语言-Python 着手,教大家如何快速入门。 一、准备工作 在开始 Python 编程之前,首先需要确保你的计算机上安装了合适的 Pytho…...

CSS3动画
在CSS3中新增了一个很有意思的东西,那就是动画,有了动画我们可以做很多的事情,让我为大家介绍一下动画吧! 本篇文章关于介绍动画,利用小球移动为你们介绍一下动画 默认样式: <!DOCTYPE html> <ht…...

黑马点评-10实现用户点赞和点赞排行榜功能
用户点赞功能 如果用户只要点赞一次就对数据库中blog表中的liked字段的值加1就会导致一个用户无限点赞 PutMapping("/like/{id}") public Result likeBlog(PathVariable("id") Long id) {// 修改点赞数量,update tb_blog set liked liked 1 where id …...
Spring配置其他注解Spring注解的解析原理
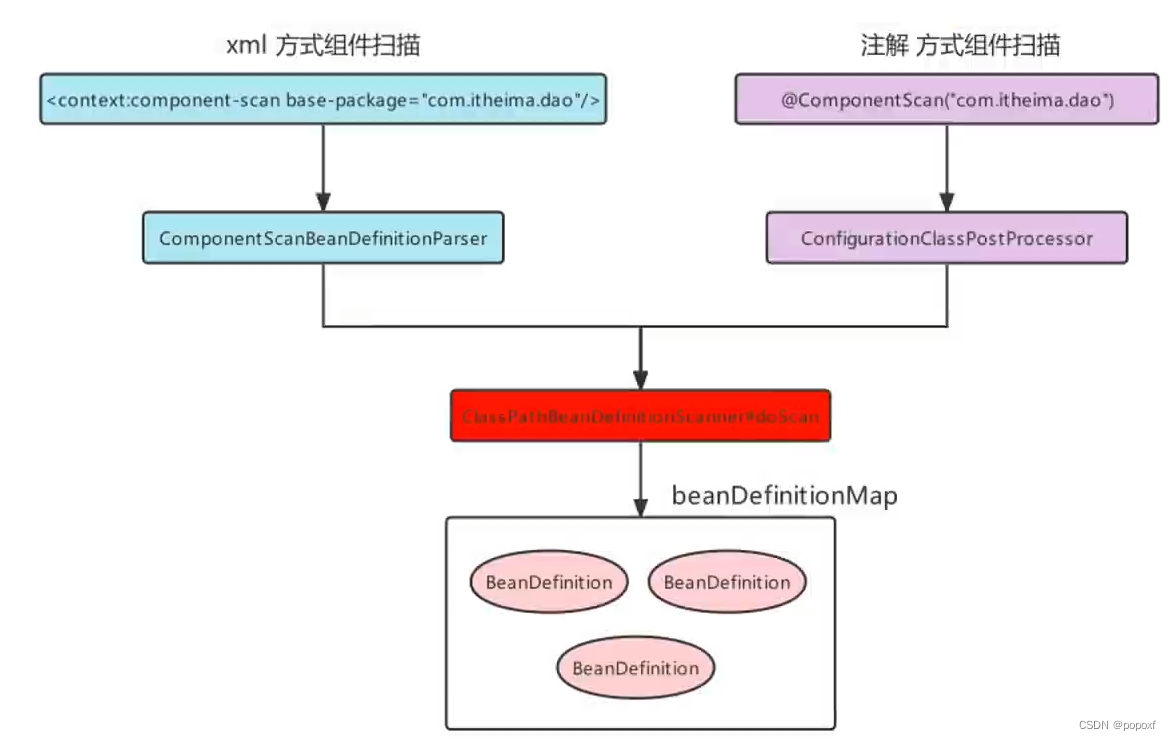
Spring配置其他注解 Primary注解用于标注相同类型的Bean优先被使用权,Primary是Spring 3.0引入的,与Component和Bean一起使用,标注该Bean的优先级更高,则在通过类型获取Bean或通过Autowired根据类型进行注入时,会选用优…...

TypeScript 学习笔记 第一部分 语法基础
【视频链接】尚硅谷TypeScript教程(李立超老师TS新课) TypeScript 1. 类型1.1 | 联合类型1.2 字面量类型1.3 any 任意类型1.4 unkown 类型1.5 as 类型断言1.6 object 对象类型1.7 { } 对象类型1.8 ? 对象中的可选属性1.9 对象中的任意属性1.1…...
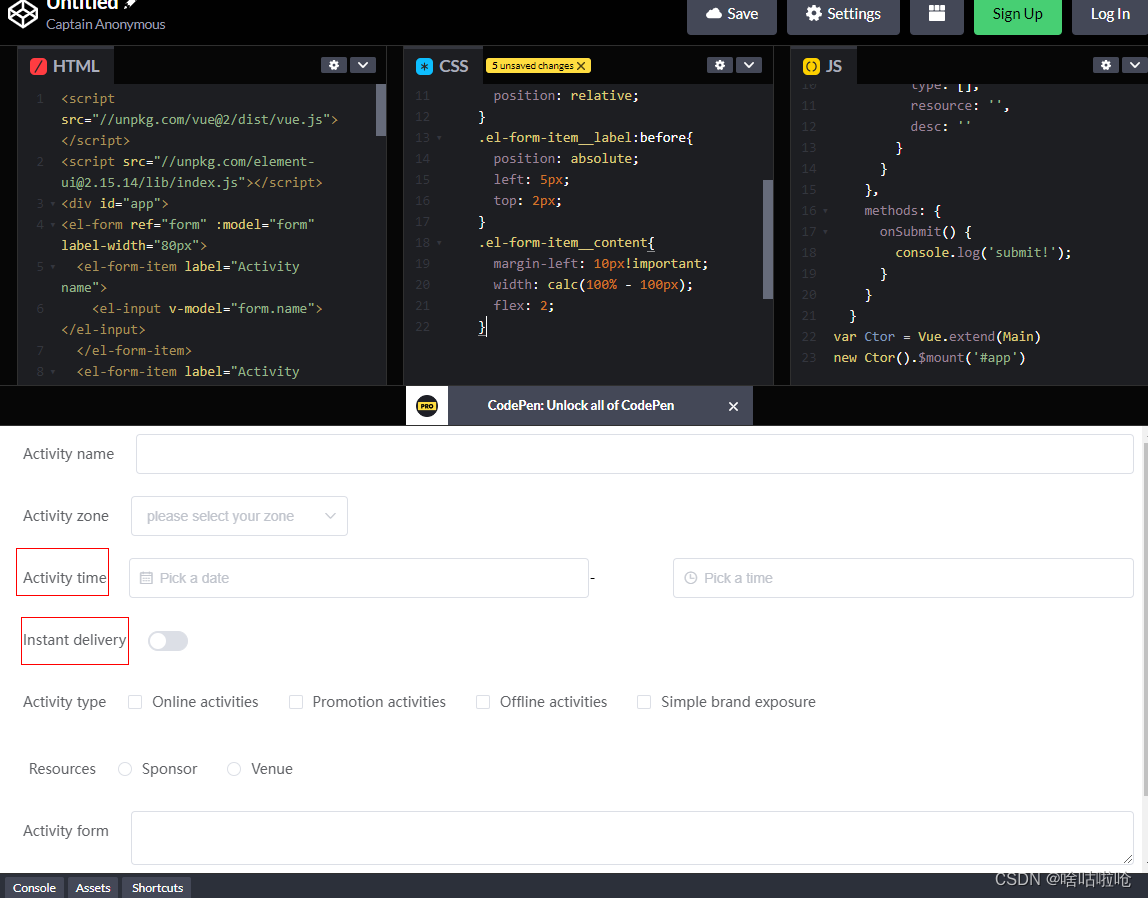
【element优化经验】怎么让element-ui中表单多语言切换排版不乱
目录 前言: 痛点: 1.左对齐,右对齐在中文和外语情况下字数不同,固定宽度会使名称换行,不在整行对齐,影响美观。 2.如果名称和输入框不在一行,会使页面越来越长 3.label-width值给变量&#…...

软件设计中如何画各类图之一实体关系图(ER图):数据库设计与分析的核心工具
目录 1 前言2 符号及作用:3 绘制清晰的ER图步骤4 实体关系图的用途5 使用场景6 实际应用场景举例7 结语 1 前言 当谈到数据库设计与分析的核心工具时,实体关系图(ER图)无疑是其中最重要的一环。在软件开发、信息管理以及数据库设…...

【神印王座】龙皓晨美妆胜过月夜,魔神皇识破无视,撮合月夜阿宝
Hello,小伙伴们,我是拾荒君。 《神印王座》国漫第82集已更新,拾荒君和大多数人一样,更新就去看了。魔神皇枫秀,威严凛然,突然空降月魔宫,整个宫殿都在这股无与伦比的强大气息中颤栗。为了顺利躲避魔神皇的…...
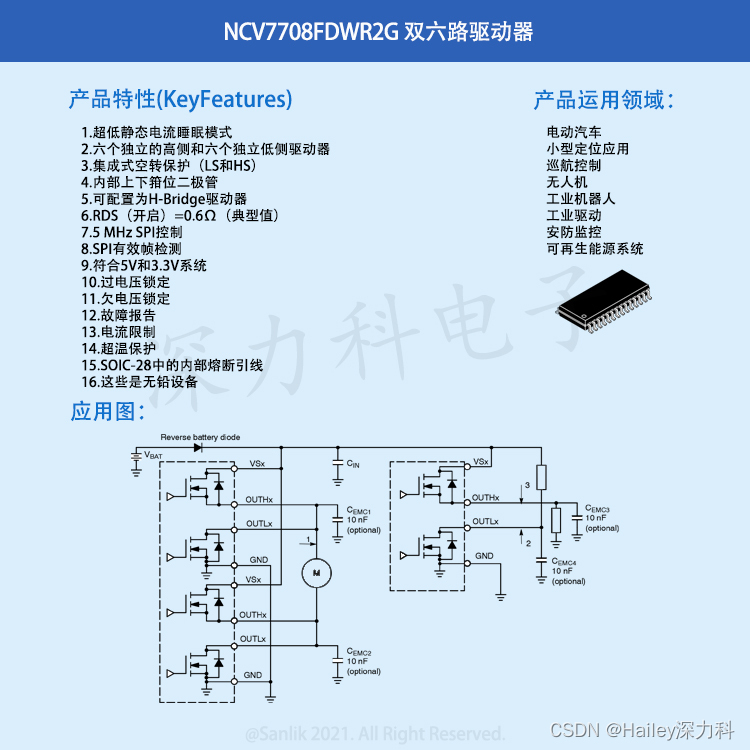
汽车级全保护型六路半桥驱动器NCV7708FDWR2G 原理、参数及应用
NCV7708FDWR2G 是一款全保护型六路半桥驱动器,特别适用于汽车和工业运动控制应用。六个高压侧和低压侧驱动器可自由配置,也可单独控制。因此可实现高压侧、低压侧和 H 桥控制。H 桥控制提供正向、逆向、制动和高阻抗状态。驱动器通过标准 SPI 接口进行控…...

【小技巧】MyBatis 中 SQL 写法技巧小总结
最近有个兄弟在搞mybatis,问我怎么写sql ,说简单一点mybatis就是写原生sql,官方都说了 mybatis 的动态sql语句是基于 OGNL表达式的。可以方便的在 sql 语句中实现某些逻辑. 总体说来mybatis 动态SQL 语句主要有以下几类: if 语句 (简单的条件…...
)
C#编程题分享(4)
换行输出整数问题 输⼊任意⼀个位数未知的整数,输出这个数每⼀位上的数字。输出的时候,从个位开始输出,每输出⼀个数字换⼀⾏。样例输⼊:3547 输出:7 换行输出 4 换行输出5 换行输出3 int n Convert.ToInt32(Conso…...
CTF靶场搭建及Web赛题制作与终端docker环境部署
♥ ♡ ♥ ♡ ♥ ♡ ♥ ♡ ♥ ♡ ♥ ♡ ♥ ♡ ♥ ♡ ♥ ♡ ♥ ♡ ♥ ♡ ♥ ♡ ♥ ♡ ♥ ♡ ♥ ♡ ♥ ♡ ♥ ♡ ♥ ♡ ♥ ♡ ♥ ♡ ♥ ♡ ♥ ♡ ♥ ♡ ♥ 写在前面 ╔═══════════════════════════════════════════════════…...
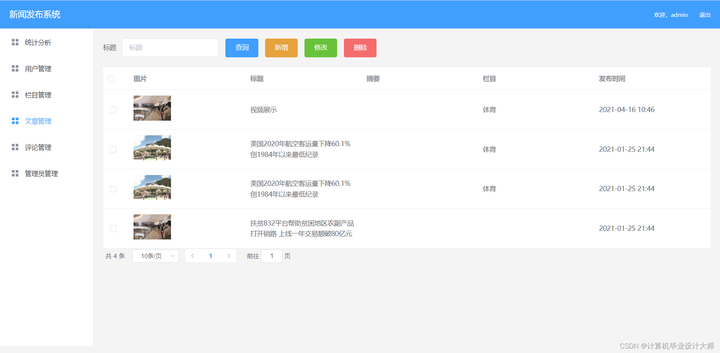
nodejs express vue uniapp新闻发布系统源码
开发技术: node.js,mysql5.7,vscode,HBuilder nodejs express vue uniapp 功能介绍: 用户端: 登录注册 首页显示搜索新闻,新闻分类,新闻列表 点击新闻进入新闻详情࿰…...
FastText模型文本分类
项目地址:NLP-Application-and-Practice/07_FastText/7.2-FastText文本分类/text_classification at master zz-zik/NLP-Application-and-Practice (github.com) 加载数据 load_data.py # coding: UTF-8 import os import pickle as pkl from tqdm import tqdmMA…...

Spark 之 入门讲解详细版(1)
1、简介 1.1 Spark简介 Spark是加州大学伯克利分校AMP实验室(Algorithms, Machines, and People Lab)开发通用内存并行计算框架。Spark在2013年6月进入Apache成为孵化项目,8个月后成为Apache顶级项目,速度之快足见过人之处&…...

Python:操作 Excel 折叠
💖亲爱的技术爱好者们,热烈欢迎来到 Kant2048 的博客!我是 Thomas Kant,很开心能在CSDN上与你们相遇~💖 本博客的精华专栏: 【自动化测试】 【测试经验】 【人工智能】 【Python】 Python 操作 Excel 系列 读取单元格数据按行写入设置行高和列宽自动调整行高和列宽水平…...

【HarmonyOS 5.0】DevEco Testing:鸿蒙应用质量保障的终极武器
——全方位测试解决方案与代码实战 一、工具定位与核心能力 DevEco Testing是HarmonyOS官方推出的一体化测试平台,覆盖应用全生命周期测试需求,主要提供五大核心能力: 测试类型检测目标关键指标功能体验基…...

java 实现excel文件转pdf | 无水印 | 无限制
文章目录 目录 文章目录 前言 1.项目远程仓库配置 2.pom文件引入相关依赖 3.代码破解 二、Excel转PDF 1.代码实现 2.Aspose.License.xml 授权文件 总结 前言 java处理excel转pdf一直没找到什么好用的免费jar包工具,自己手写的难度,恐怕高级程序员花费一年的事件,也…...

Swift 协议扩展精进之路:解决 CoreData 托管实体子类的类型不匹配问题(下)
概述 在 Swift 开发语言中,各位秃头小码农们可以充分利用语法本身所带来的便利去劈荆斩棘。我们还可以恣意利用泛型、协议关联类型和协议扩展来进一步简化和优化我们复杂的代码需求。 不过,在涉及到多个子类派生于基类进行多态模拟的场景下,…...

渲染学进阶内容——模型
最近在写模组的时候发现渲染器里面离不开模型的定义,在渲染的第二篇文章中简单的讲解了一下关于模型部分的内容,其实不管是方块还是方块实体,都离不开模型的内容 🧱 一、CubeListBuilder 功能解析 CubeListBuilder 是 Minecraft Java 版模型系统的核心构建器,用于动态创…...

页面渲染流程与性能优化
页面渲染流程与性能优化详解(完整版) 一、现代浏览器渲染流程(详细说明) 1. 构建DOM树 浏览器接收到HTML文档后,会逐步解析并构建DOM(Document Object Model)树。具体过程如下: (…...
指令的指南)
在Ubuntu中设置开机自动运行(sudo)指令的指南
在Ubuntu系统中,有时需要在系统启动时自动执行某些命令,特别是需要 sudo权限的指令。为了实现这一功能,可以使用多种方法,包括编写Systemd服务、配置 rc.local文件或使用 cron任务计划。本文将详细介绍这些方法,并提供…...
详解:相对定位 绝对定位 固定定位)
css的定位(position)详解:相对定位 绝对定位 固定定位
在 CSS 中,元素的定位通过 position 属性控制,共有 5 种定位模式:static(静态定位)、relative(相对定位)、absolute(绝对定位)、fixed(固定定位)和…...

【学习笔记】深入理解Java虚拟机学习笔记——第4章 虚拟机性能监控,故障处理工具
第2章 虚拟机性能监控,故障处理工具 4.1 概述 略 4.2 基础故障处理工具 4.2.1 jps:虚拟机进程状况工具 命令:jps [options] [hostid] 功能:本地虚拟机进程显示进程ID(与ps相同),可同时显示主类&#x…...
