【附代码】判断线段是否相交算法(Python,C++)
【附代码】判断线段是否相交算法(Python,C++)
文章目录
- 【附代码】判断线段是否相交算法(Python,C++)
- 相关文献
- 测试电脑配置
- 基础
- 向量旋转
- 向量缩放
- 向量投影
- 推导
- 点乘
- 定义
- 推导
- 几何意义
- 叉乘
- 定义
- 推导
- 几何意义
- 判断线段是否相交
- 代码
- C++
- Python
- 画图代码
- 测试结果
作者:小猪快跑
基础数学&计算数学,从事优化领域5年+,主要研究方向:MIP求解器、整数规划、随机规划、智能优化算法
如有错误,欢迎指正。如有更好的算法,也欢迎交流!!!——@小猪快跑
相关文献
测试电脑配置
博主三千元电脑的渣渣配置:
CPU model: AMD Ryzen 7 7840HS w/ Radeon 780M Graphics, instruction set [SSE2|AVX|AVX2|AVX512]
Thread count: 8 physical cores, 16 logical processors, using up to 16 threads
基础
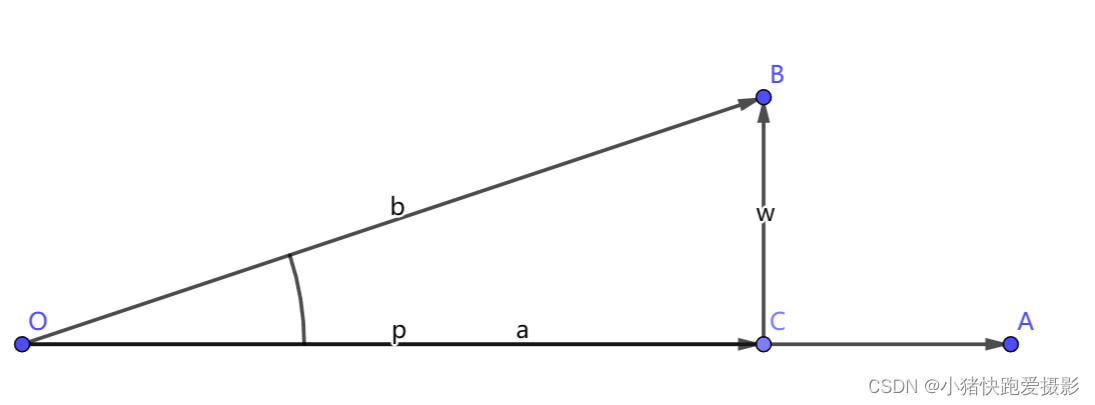
这里假设:
O A → = a ⃗ = ( x a , y a ) O B → = b ⃗ = ( x b , y b ) O C → = p ⃗ = ( x c , y c ) C B → = w ⃗ ∠ A O B = α \overrightarrow{OA} = \vec{a} = (x_a,y_a) \\ \overrightarrow{OB} = \vec{b} = (x_b,y_b) \\ \overrightarrow{OC} = \vec{p} = (x_c,y_c) \\ \overrightarrow{CB} = \vec{w} \\ ∠AOB = \alpha OA=a=(xa,ya)OB=b=(xb,yb)OC=p=(xc,yc)CB=w∠AOB=α
向量旋转
任意向量都能表示成:
( r cos α r sin α ) \left ( \begin{matrix} r\cos{\alpha} \\ r\sin{\alpha} \\ \end{matrix} \right ) (rcosαrsinα)
假设向量逆时针旋转了 β \beta β,那么我们容易知道旋转后向量是:
( r cos ( α + β ) r sin ( α + β ) ) \left ( \begin{matrix} r\cos({\alpha + \beta}) \\ r\sin({\alpha + \beta}) \\ \end{matrix} \right ) (rcos(α+β)rsin(α+β))
那么容易得到:
( r cos ( α + β ) r sin ( α + β ) ) = ( cos α − sin α sin α cos α ) ( r cos α r sin α ) \left ( \begin{matrix} r\cos({\alpha + \beta}) \\ r\sin({\alpha + \beta}) \\ \end{matrix} \right )= \left ( \begin{array}{rr} \cos{\alpha} & -\sin{\alpha} \\ \sin{\alpha} & \cos{\alpha} \\ \end{array} \right ) \left ( \begin{matrix} r\cos{\alpha} \\ r\sin{\alpha} \\ \end{matrix} \right ) (rcos(α+β)rsin(α+β))=(cosαsinα−sinαcosα)(rcosαrsinα)
于是旋转向量就是:
( cos α − sin α sin α cos α ) \left ( \begin{array}{rr} \cos{\alpha} & -\sin{\alpha} \\ \sin{\alpha} & \cos{\alpha} \\ \end{array} \right ) (cosαsinα−sinαcosα)
向量缩放
( r 0 0 r ) \left ( \begin{array}{rr} r & 0 \\ 0 & r \\ \end{array} \right ) (r00r)
向量投影
推导
主要利用 O C → \overrightarrow{OC} OC 和 C B → \overrightarrow{CB} CB 垂直,点积为0:
w ⃗ = b ⃗ − p ⃗ w ⃗ ⋅ p ⃗ = 0 } ⇒ ( b ⃗ − p ⃗ ) ⋅ p ⃗ = 0 p ⃗ = k a ⃗ } ⇒ ( b ⃗ − k a ⃗ ) ⋅ k a ⃗ = 0 p ⃗ = k a ⃗ } ⇒ p ⃗ = a ⃗ ⋅ b ⃗ a ⃗ ⋅ a ⃗ a ⃗ \left. \begin{array}{r} \left. \begin{array}{l} \vec{w}=\vec{b}-\vec{p} \\ \vec{w} \cdot \vec{p} = 0 \end{array} \right\} \Rightarrow (\vec{b}-\vec{p}) \cdot \vec{p} = 0\\ \vec{p} = k \vec{a} \end{array} \right\} \Rightarrow \left. \begin{array}{r} (\vec{b}-k \vec{a}) \cdot k \vec{a} = 0 \\ \vec{p} = k \vec{a} \end{array} \right\} \Rightarrow \vec{p} = \frac{\vec{a} \cdot \vec{b}}{\vec{a} \cdot \vec{a}} \vec{a} w=b−pw⋅p=0}⇒(b−p)⋅p=0p=ka⎭ ⎬ ⎫⇒(b−ka)⋅ka=0p=ka}⇒p=a⋅aa⋅ba
那么投影矩阵
P b ⃗ = p ⃗ = a ⃗ a ⃗ ⋅ b ⃗ a ⃗ ⋅ a ⃗ ⇒ P = a ⃗ a ⃗ T a ⃗ T a ⃗ \begin{array}{l} & P\vec{b} = \vec{p} = \vec{a} \frac{\vec{a} \cdot \vec{b}}{\vec{a} \cdot \vec{a}} \\ \Rightarrow & P = \frac{\vec{a}\vec{a}^T}{\vec{a}^T\vec{a}} \end{array} ⇒Pb=p=aa⋅aa⋅bP=aTaaaT
点乘
点乘(Dot Product)的结果是点积,又称数量积或标量积(Scalar Product)
定义
a ⃗ ⋅ b ⃗ = ∣ a ⃗ ∣ ∣ b ⃗ ∣ cos α \vec{a} \cdot \vec{b} = |\vec{a}||\vec{b}|\cos{\alpha} a⋅b=∣a∣∣b∣cosα
推导
那么如何用解析几何来表示呢?
我们其实可以把 a ⃗ \vec{a} a 旋转 α \alpha α 再缩放 ∣ b ⃗ ∣ / ∣ a ⃗ ∣ |\vec{b}|/|\vec{a}| ∣b∣/∣a∣ 倍,就是 b ⃗ \vec{b} b 了:
( ∣ b ⃗ ∣ ∣ a ⃗ ∣ 0 0 ∣ b ⃗ ∣ ∣ a ⃗ ∣ ) ( cos α − sin α sin α cos α ) ( x a y a ) = ( x b y b ) ⇒ ( ( x a cos α − y a sin α ) ∣ b ⃗ ∣ ( x a sin α + y a cos α ) ∣ b ⃗ ∣ ) = ( x b ∣ a ⃗ ∣ y b ∣ a ⃗ ∣ ) ⇒ ∣ a ⃗ ∣ ∣ b ⃗ ∣ cos α = x a x b + y a y b \begin{array}{l} &\left ( \begin{matrix} \frac{|\vec{b}|}{|\vec{a}|} & 0 \\ 0 & \frac{|\vec{b}|}{|\vec{a}|} \\ \end{matrix} \right ) \left ( \begin{array}{rr} \cos{\alpha} & -\sin{\alpha} \\ \sin{\alpha} & \cos{\alpha} \\ \end{array} \right ) \left ( \begin{matrix} x_a \\ y_a \\ \end{matrix} \right )= \left ( \begin{matrix} x_b \\ y_b \\ \end{matrix} \right ) \\ \Rightarrow & \left ( \begin{matrix} (x_a\cos{\alpha} - y_a\sin{\alpha})|\vec{b}| \\ (x_a\sin{\alpha} + y_a\cos{\alpha})|\vec{b}| \\ \end{matrix} \right )= \left ( \begin{matrix} x_b|\vec{a}| \\ y_b|\vec{a}| \\ \end{matrix} \right ) \\ \Rightarrow & |\vec{a}||\vec{b}|\cos{\alpha} = x_a x_b + y_a y_b \end{array} ⇒⇒ ∣a∣∣b∣00∣a∣∣b∣ (cosαsinα−sinαcosα)(xaya)=(xbyb)((xacosα−yasinα)∣b∣(xasinα+yacosα)∣b∣)=(xb∣a∣yb∣a∣)∣a∣∣b∣cosα=xaxb+yayb
几何意义
点乘的结果表示 a ⃗ \vec{a} a 在 b ⃗ \vec{b} b 方向上的投影与 b ⃗ \vec{b} b 的乘积,反映了两个向量在方向上的相似度,结果越大越相似。基于结果可以判断这两个向量是否是同一方向,是否正交垂直,具体对应关系为:
- a ⃗ ⋅ b ⃗ > 0 \vec{a} \cdot \vec{b} > 0 a⋅b>0 则方向基本相同,夹角在0°到90°之间
- a ⃗ ⋅ b ⃗ = 0 \vec{a} \cdot \vec{b} = 0 a⋅b=0 则正交,相互垂直
- a ⃗ ⋅ b ⃗ < 0 \vec{a} \cdot \vec{b} < 0 a⋅b<0 则方向基本相反,夹角在90°到180°之间
叉乘
叉乘(Cross Product)又称向量积(Vector Product)。
定义
a ⃗ × b ⃗ = ∣ a ⃗ ∣ ∣ b ⃗ ∣ sin α \vec{a} \times \vec{b} = |\vec{a}||\vec{b}|\sin{\alpha} a×b=∣a∣∣b∣sinα
推导
那么如何用解析几何来表示呢?
我们其实可以把 a ⃗ \vec{a} a 旋转 α \alpha α 再缩放 ∣ b ⃗ ∣ / ∣ a ⃗ ∣ |\vec{b}|/|\vec{a}| ∣b∣/∣a∣ 倍,就是 b ⃗ \vec{b} b 了:
( ∣ b ⃗ ∣ ∣ a ⃗ ∣ 0 0 ∣ b ⃗ ∣ ∣ a ⃗ ∣ ) ( cos α − sin α sin α cos α ) ( x a y a ) = ( x b y b ) ⇒ ( ( x a cos α − y a sin α ) ∣ b ⃗ ∣ ( x a sin α + y a cos α ) ∣ b ⃗ ∣ ) = ( x b ∣ a ⃗ ∣ y b ∣ a ⃗ ∣ ) ⇒ ∣ a ⃗ ∣ ∣ b ⃗ ∣ sin α = x a y b − x b y a \begin{array}{l} & \left ( \begin{matrix} \frac{|\vec{b}|}{|\vec{a}|} & 0 \\ 0 & \frac{|\vec{b}|}{|\vec{a}|} \\ \end{matrix} \right ) \left ( \begin{array}{rr} \cos{\alpha} & -\sin{\alpha} \\ \sin{\alpha} & \cos{\alpha} \\ \end{array} \right ) \left ( \begin{matrix} x_a \\ y_a \\ \end{matrix} \right )= \left ( \begin{matrix} x_b \\ y_b \\ \end{matrix} \right ) \\ \Rightarrow & \left ( \begin{matrix} (x_a\cos{\alpha} - y_a\sin{\alpha})|\vec{b}| \\ (x_a\sin{\alpha} + y_a\cos{\alpha})|\vec{b}| \\ \end{matrix} \right )= \left ( \begin{matrix} x_b|\vec{a}| \\ y_b|\vec{a}| \\ \end{matrix} \right ) \\ \Rightarrow & |\vec{a}||\vec{b}|\sin{\alpha} = x_a y_b - x_b y_a \end{array} ⇒⇒ ∣a∣∣b∣00∣a∣∣b∣ (cosαsinα−sinαcosα)(xaya)=(xbyb)((xacosα−yasinα)∣b∣(xasinα+yacosα)∣b∣)=(xb∣a∣yb∣a∣)∣a∣∣b∣sinα=xayb−xbya
几何意义
如果以向量 a ⃗ \vec{a} a 和 b ⃗ \vec{b} b 为边构成一个平行四边形,那么这两个向量外积的模长与这个平行四边形的面积相等。
判断线段是否相交
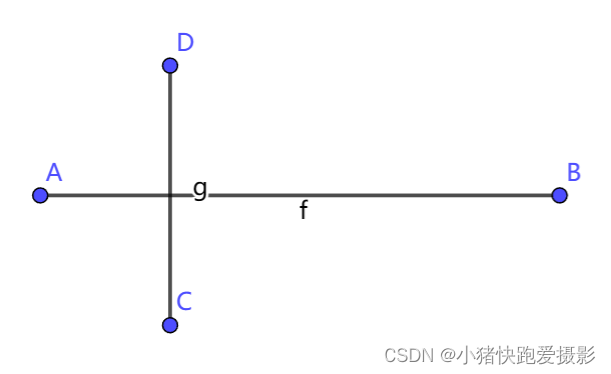
我们有了上面的基础后,其实思路就一下打开了!
其实我们只要想着 A B → \overrightarrow{AB} AB 的两边是 C C C 和 D D D ,那么也就是说 A B → × A D → \overrightarrow{AB} \times \overrightarrow{AD} AB×AD 和 A B → × A C → \overrightarrow{AB} \times \overrightarrow{AC} AB×AC 有正有负,同时呢 C D → × C A → \overrightarrow{CD} \times \overrightarrow{CA} CD×CA 和 C D → × C B → \overrightarrow{CD} \times \overrightarrow{CB} CD×CB 有正有负(这里要注意一下叉乘可能为0的情况,比如说 A A A 在 C D → \overrightarrow{CD} CD 上)。这里我们有正有负采用直接判断而不是相乘小于零,这是因为相乘可能存在数值溢出等问题。而且一般的,和零的判断比乘法快很多。
我们直接上测试用例看看效果!!!
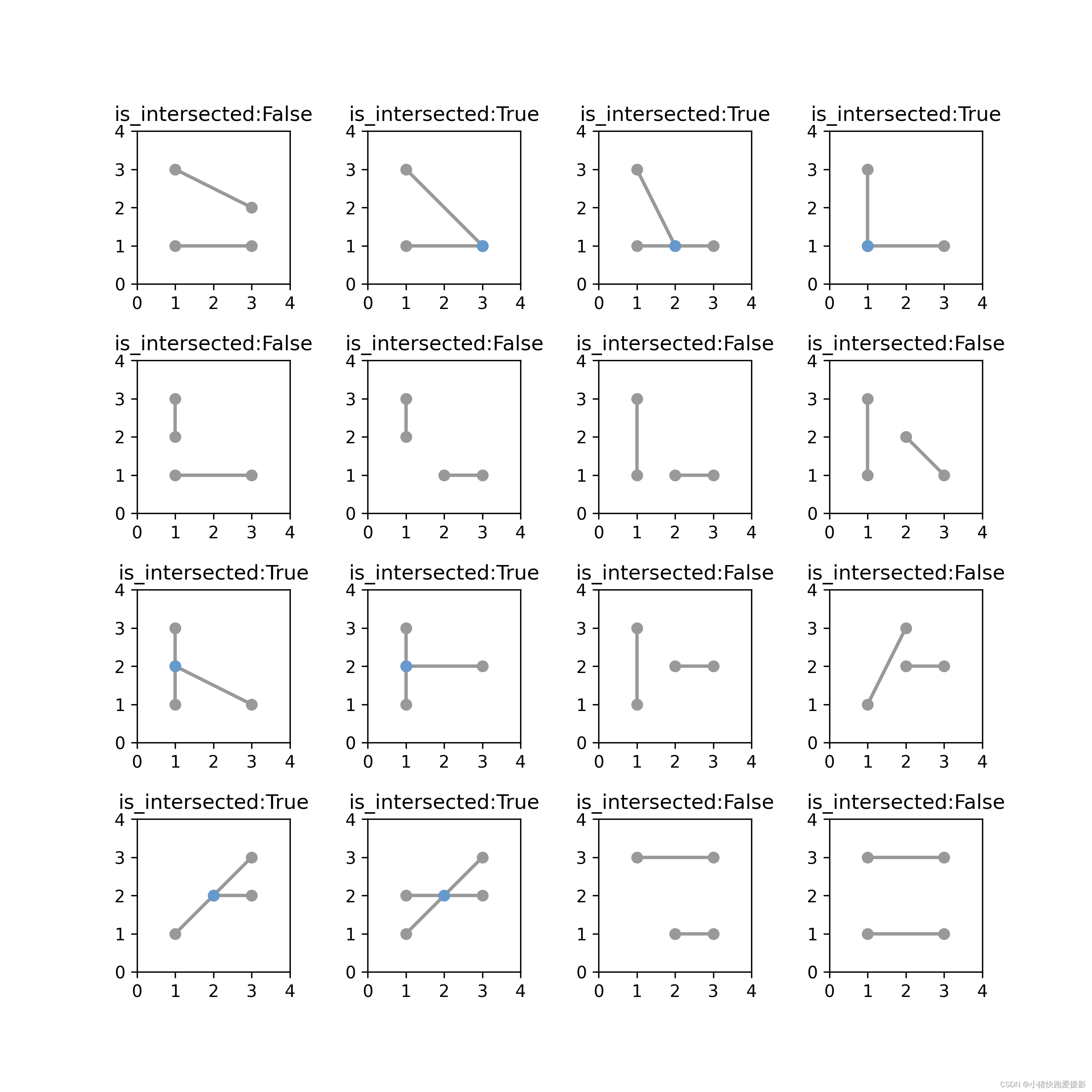
代码
C++
#include <iostream>
#include <chrono>using namespace std;int cross_product(int x1, int y1, int x2, int y2) {// 计算向量 (x1, y1) 和向量 (x2, y2) 的叉积return x1 * y2 - x2 * y1;
}int dot_product(int x1, int y1, int x2, int y2) {// 计算向量 (x1, y1) 和向量 (x2, y2) 的点乘return x1 * x2 + y1 * y2;
}bool is_intersected(int x1, int y1, int x2, int y2, int x3, int y3, int x4, int y4) {/*判断线段 (x1, y1)-(x2, y2) 和线段 (x3, y3)-(x4, y4) 是否相交AB×ACAB×ADCD×CACD×CB*/if ((max(x1, x2) < min(x3, x4)) or (max(x3, x4) < min(x1, x2)) or (max(y1, y2) < min(y3, y4)) or (max(y3, y4) < min(y1, y2))) {return false;}int abx = x2 - x1;int aby = y2 - y1;int acx = x3 - x1;int acy = y3 - y1;int adx = x4 - x1;int ady = y4 - y1;int bcx = x3 - x2;int bcy = y3 - y2;int cdx = x4 - x3;int cdy = y4 - y3;int cp1 = cross_product(abx, aby, acx, acy);int cp2 = cross_product(abx, aby, adx, ady);int cp3 = cross_product(cdx, cdy, -acx, -acy);int cp4 = cross_product(cdx, cdy, -bcx, -bcy);// 如果两个叉积的乘积小于0,则两个向量在向量 (x1, y1)-(x2, y2) 的两侧,即线段相交if (((cp1 > 0 and 0 > cp2) or (cp1 < 0 and 0 < cp2) or cp1 == 0 or cp2 == 0) and((cp3 > 0 and 0 > cp4) or (cp3 < 0 and 0 < cp4) or cp3 == 0 or cp4 == 0)) {return true;}return false;
}int test(int n) {int res = 0;for (auto x1 = 0; x1 < n; x1++) {for (auto y1 = 0; y1 < n; y1++) {for (auto x2 = 0; x2 < n; x2++) {for (auto y2 = 0; y2 < n; y2++) {if (x1 == x2 and y1 == y2) {continue;}for (auto x3 = 0; x3 < n; x3++) {for (auto y3 = 0; y3 < n; y3++) {for (auto x4 = 0; x4 < n; x4++) {for (auto y4 = 0; y4 < n; y4++) {if (x3 == x4 and y3 == y4) {continue;}res += is_intersected(x1, y1, x2, y2, x3, y3, x4, y4);}}}}}}}}return res;
}int main() {auto start = std::chrono::high_resolution_clock::now();std::cout << test(7) << std::endl;auto finish = std::chrono::high_resolution_clock::now();std::chrono::duration<double> elapsed = finish - start;std::cout << "Elapsed time: " << elapsed.count() << " s\n" << std::endl;return 0;
}
Python
from time import time
import math
from numba import njit@njit
def cross_product(x1, y1, x2, y2):"""计算向量 (x1, y1) 和向量 (x2, y2) 的叉积"""return x1 * y2 - x2 * y1@njit
def dot_product(x1, y1, x2, y2):"""计算向量 (x1, y1) 和向量 (x2, y2) 的点乘"""return x1 * x2 + y1 * y2@njit
def is_intersected(x1, y1, x2, y2, x3, y3, x4, y4):"""判断线段 (x1, y1)-(x2, y2) 和线段 (x3, y3)-(x4, y4) 是否相交AB×ACAB×ADCD×CACD×CB"""if (max(x1, x2) < min(x3, x4)) or (max(x3, x4) < min(x1, x2)) or (max(y1, y2) < min(y3, y4)) or (max(y3, y4) < min(y1, y2)):return Falseabx = x2 - x1aby = y2 - y1acx = x3 - x1acy = y3 - y1adx = x4 - x1ady = y4 - y1bcx = x3 - x2bcy = y3 - y2cdx = x4 - x3cdy = y4 - y3cp1 = cross_product(abx, aby, acx, acy)cp2 = cross_product(abx, aby, adx, ady)cp3 = cross_product(cdx, cdy, -acx, -acy)cp4 = cross_product(cdx, cdy, -bcx, -bcy)# 如果两个叉积的乘积小于0,则两个向量在向量 (x1, y1)-(x2, y2) 的两侧,即线段相交if ((cp1 > 0 > cp2) or (cp1 < 0 < cp2) or cp1 == 0 or cp2 == 0) and ((cp3 > 0 > cp4) or (cp3 < 0 < cp4) or cp3 == 0 or cp4 == 0):return Truereturn Falsedef test(n):res = 0for x1 in range(n):for y1 in range(n):for x2 in range(n):for y2 in range(n):if x1 == x2 and y1 == y2:continuefor x3 in range(n):for y3 in range(n):for x4 in range(n):for y4 in range(n):if x3 == x4 and y3 == y4:continueres += is_intersected(x1, y1, x2, y2, x3, y3, x4, y4)return resif __name__ == '__main__':s = time()print(test(7))print(time() - s)
画图代码
# main.py
import matplotlib.pyplot as plt
from shapely.geometry import Point, LineString, Polygon
from shapely.plotting import plot_polygon, plot_points, plot_linefrom csdn_line_intersect import is_intersected
from figures import BLUE, GRAY, set_limitsfig = plt.figure(1, figsize=(9, 9), dpi=300)
fig.subplots_adjust(wspace=0.5, hspace=0.5) # 调整边距和子图的间距ax = fig.add_subplot(4, 4, 1)
x1, y1, x2, y2 = 1, 1, 3, 1
x3, y3, x4, y4 = 1, 3, 3, 2
a = LineString([(x1, y1), (x2, y2)])
b = LineString([(x3, y3), (x4, y4)])
plot_line(a, ax=ax, color=GRAY)
plot_line(b, ax=ax, color=GRAY)
plot_points(a.intersection(b), ax=ax, color=BLUE)
ax.set_title(f'is_intersected:{is_intersected(x1, y1, x2, y2, x3, y3, x4, y4)}')
set_limits(ax, 0, 4, 0, 4)ax = fig.add_subplot(4, 4, 2)
x1, y1, x2, y2 = 1, 1, 3, 1
x3, y3, x4, y4 = 1, 3, 3, 1
a = LineString([(x1, y1), (x2, y2)])
b = LineString([(x3, y3), (x4, y4)])
plot_line(a, ax=ax, color=GRAY)
plot_line(b, ax=ax, color=GRAY)
plot_points(a.intersection(b), ax=ax, color=BLUE)
ax.set_title(f'is_intersected:{is_intersected(x1, y1, x2, y2, x3, y3, x4, y4)}')
set_limits(ax, 0, 4, 0, 4)ax = fig.add_subplot(4, 4, 3)
x1, y1, x2, y2 = 1, 1, 3, 1
x3, y3, x4, y4 = 1, 3, 2, 1
a = LineString([(x1, y1), (x2, y2)])
b = LineString([(x3, y3), (x4, y4)])
plot_line(a, ax=ax, color=GRAY)
plot_line(b, ax=ax, color=GRAY)
plot_points(a.intersection(b), ax=ax, color=BLUE)
ax.set_title(f'is_intersected:{is_intersected(x1, y1, x2, y2, x3, y3, x4, y4)}')
set_limits(ax, 0, 4, 0, 4)ax = fig.add_subplot(4, 4, 4)
x1, y1, x2, y2 = 1, 1, 3, 1
x3, y3, x4, y4 = 1, 3, 1, 1
a = LineString([(x1, y1), (x2, y2)])
b = LineString([(x3, y3), (x4, y4)])
plot_line(a, ax=ax, color=GRAY)
plot_line(b, ax=ax, color=GRAY)
plot_points(a.intersection(b), ax=ax, color=BLUE)
ax.set_title(f'is_intersected:{is_intersected(x1, y1, x2, y2, x3, y3, x4, y4)}')
set_limits(ax, 0, 4, 0, 4)ax = fig.add_subplot(4, 4, 5)
x1, y1, x2, y2 = 1, 1, 3, 1
x3, y3, x4, y4 = 1, 3, 1, 2
a = LineString([(x1, y1), (x2, y2)])
b = LineString([(x3, y3), (x4, y4)])
plot_line(a, ax=ax, color=GRAY)
plot_line(b, ax=ax, color=GRAY)
plot_points(a.intersection(b), ax=ax, color=BLUE)
ax.set_title(f'is_intersected:{is_intersected(x1, y1, x2, y2, x3, y3, x4, y4)}')
set_limits(ax, 0, 4, 0, 4)ax = fig.add_subplot(4, 4, 6)
x1, y1, x2, y2 = 2, 1, 3, 1
x3, y3, x4, y4 = 1, 3, 1, 2
a = LineString([(x1, y1), (x2, y2)])
b = LineString([(x3, y3), (x4, y4)])
plot_line(a, ax=ax, color=GRAY)
plot_line(b, ax=ax, color=GRAY)
plot_points(a.intersection(b), ax=ax, color=BLUE)
ax.set_title(f'is_intersected:{is_intersected(x1, y1, x2, y2, x3, y3, x4, y4)}')
set_limits(ax, 0, 4, 0, 4)ax = fig.add_subplot(4, 4, 7)
x1, y1, x2, y2 = 2, 1, 3, 1
x3, y3, x4, y4 = 1, 3, 1, 1
a = LineString([(x1, y1), (x2, y2)])
b = LineString([(x3, y3), (x4, y4)])
plot_line(a, ax=ax, color=GRAY)
plot_line(b, ax=ax, color=GRAY)
plot_points(a.intersection(b), ax=ax, color=BLUE)
ax.set_title(f'is_intersected:{is_intersected(x1, y1, x2, y2, x3, y3, x4, y4)}')
set_limits(ax, 0, 4, 0, 4)ax = fig.add_subplot(4, 4, 8)
x1, y1, x2, y2 = 2, 2, 3, 1
x3, y3, x4, y4 = 1, 3, 1, 1
a = LineString([(x1, y1), (x2, y2)])
b = LineString([(x3, y3), (x4, y4)])
plot_line(a, ax=ax, color=GRAY)
plot_line(b, ax=ax, color=GRAY)
plot_points(a.intersection(b), ax=ax, color=BLUE)
ax.set_title(f'is_intersected:{is_intersected(x1, y1, x2, y2, x3, y3, x4, y4)}')
set_limits(ax, 0, 4, 0, 4)ax = fig.add_subplot(4, 4, 9)
x1, y1, x2, y2 = 1, 2, 3, 1
x3, y3, x4, y4 = 1, 3, 1, 1
a = LineString([(x1, y1), (x2, y2)])
b = LineString([(x3, y3), (x4, y4)])
plot_line(a, ax=ax, color=GRAY)
plot_line(b, ax=ax, color=GRAY)
plot_points(a.intersection(b), ax=ax, color=BLUE)
ax.set_title(f'is_intersected:{is_intersected(x1, y1, x2, y2, x3, y3, x4, y4)}')
set_limits(ax, 0, 4, 0, 4)ax = fig.add_subplot(4, 4, 10)
x1, y1, x2, y2 = 1, 2, 3, 2
x3, y3, x4, y4 = 1, 3, 1, 1
a = LineString([(x1, y1), (x2, y2)])
b = LineString([(x3, y3), (x4, y4)])
plot_line(a, ax=ax, color=GRAY)
plot_line(b, ax=ax, color=GRAY)
plot_points(a.intersection(b), ax=ax, color=BLUE)
ax.set_title(f'is_intersected:{is_intersected(x1, y1, x2, y2, x3, y3, x4, y4)}')
set_limits(ax, 0, 4, 0, 4)ax = fig.add_subplot(4, 4, 11)
x1, y1, x2, y2 = 2, 2, 3, 2
x3, y3, x4, y4 = 1, 3, 1, 1
a = LineString([(x1, y1), (x2, y2)])
b = LineString([(x3, y3), (x4, y4)])
plot_line(a, ax=ax, color=GRAY)
plot_line(b, ax=ax, color=GRAY)
plot_points(a.intersection(b), ax=ax, color=BLUE)
ax.set_title(f'is_intersected:{is_intersected(x1, y1, x2, y2, x3, y3, x4, y4)}')
set_limits(ax, 0, 4, 0, 4)ax = fig.add_subplot(4, 4, 12)
x1, y1, x2, y2 = 2, 2, 3, 2
x3, y3, x4, y4 = 2, 3, 1, 1
a = LineString([(x1, y1), (x2, y2)])
b = LineString([(x3, y3), (x4, y4)])
plot_line(a, ax=ax, color=GRAY)
plot_line(b, ax=ax, color=GRAY)
plot_points(a.intersection(b), ax=ax, color=BLUE)
ax.set_title(f'is_intersected:{is_intersected(x1, y1, x2, y2, x3, y3, x4, y4)}')
set_limits(ax, 0, 4, 0, 4)ax = fig.add_subplot(4, 4, 13)
x1, y1, x2, y2 = 2, 2, 3, 2
x3, y3, x4, y4 = 3, 3, 1, 1
a = LineString([(x1, y1), (x2, y2)])
b = LineString([(x3, y3), (x4, y4)])
plot_line(a, ax=ax, color=GRAY)
plot_line(b, ax=ax, color=GRAY)
plot_points(a.intersection(b), ax=ax, color=BLUE)
ax.set_title(f'is_intersected:{is_intersected(x1, y1, x2, y2, x3, y3, x4, y4)}')
set_limits(ax, 0, 4, 0, 4)ax = fig.add_subplot(4, 4, 14)
x1, y1, x2, y2 = 1, 2, 3, 2
x3, y3, x4, y4 = 3, 3, 1, 1
a = LineString([(x1, y1), (x2, y2)])
b = LineString([(x3, y3), (x4, y4)])
plot_line(a, ax=ax, color=GRAY)
plot_line(b, ax=ax, color=GRAY)
plot_points(a.intersection(b), ax=ax, color=BLUE)
ax.set_title(f'is_intersected:{is_intersected(x1, y1, x2, y2, x3, y3, x4, y4)}')
set_limits(ax, 0, 4, 0, 4)ax = fig.add_subplot(4, 4, 15)
x1, y1, x2, y2 = 2, 1, 3, 1
x3, y3, x4, y4 = 1, 3, 3, 3
a = LineString([(x1, y1), (x2, y2)])
b = LineString([(x3, y3), (x4, y4)])
plot_line(a, ax=ax, color=GRAY)
plot_line(b, ax=ax, color=GRAY)
plot_points(a.intersection(b), ax=ax, color=BLUE)
ax.set_title(f'is_intersected:{is_intersected(x1, y1, x2, y2, x3, y3, x4, y4)}')
set_limits(ax, 0, 4, 0, 4)ax = fig.add_subplot(4, 4, 16)
x1, y1, x2, y2 = 1, 1, 3, 1
x3, y3, x4, y4 = 1, 3, 3, 3
a = LineString([(x1, y1), (x2, y2)])
b = LineString([(x3, y3), (x4, y4)])
plot_line(a, ax=ax, color=GRAY)
plot_line(b, ax=ax, color=GRAY)
plot_points(a.intersection(b), ax=ax, color=BLUE)
ax.set_title(f'is_intersected:{is_intersected(x1, y1, x2, y2, x3, y3, x4, y4)}')
set_limits(ax, 0, 4, 0, 4)plt.savefig('output.png')
plt.show()
测试结果
C++: 0.0157648 s
Python(numba): 1.3376786708831787 s
Python(no numba): 3.585803985595703 s
Python(shapely): 73.45080494880676 s
相关文章:

【附代码】判断线段是否相交算法(Python,C++)
【附代码】判断线段是否相交算法(Python,C) 文章目录 【附代码】判断线段是否相交算法(Python,C)相关文献测试电脑配置基础向量旋转向量缩放向量投影推导 点乘定义推导几何意义 叉乘定义推导几何意义 判断线…...

PDF控件Spire.PDF for .NET【转换】演示:将 PDF 转换为 word、HTML、SVG、XPS
本文我们将演示如何通过调用 Spire.PDF 提供的方法 PdfDocument.SaveToStream() 将 PDF 页面转换为 HTML、Word、SVG、XPS、PDF 并将它们保存到流中。并且从Spire.PDF版本4.3开始,它新支持转换定义范围的PDF页面并将其保存到流中。 Spire.Doc 是一款专门对 Word 文…...
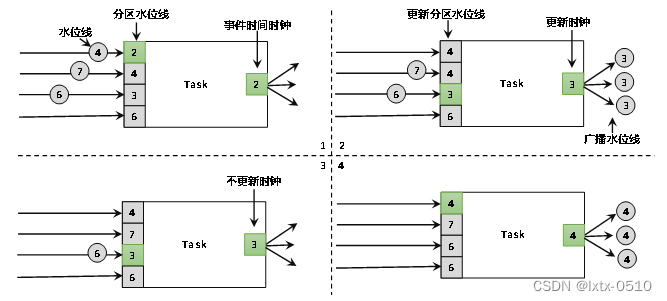
【FLink】水位线(Watermark)
目录 1、关于时间语义 1.1事件时间 1.2处理时间编辑 2、什么是水位线 2.1 顺序流和乱序流 2.2乱序数据的处理 2.3 水位线的特性 3 、水位线的生成 3.1 生成水位线的总体原则 3.2 水位线生成策略 3.3 Flink内置水位线 3.3.1 有序流中内置水位线设置 3.4.2 断点式…...

github访问不了问题
git clone github上的项目的时候,不是访问不了,就是克隆过程被中断了 最近找到一个代理,从代理那里clone而不是github上 GitHub代理 – 初果编程...
【Java】认识String类
文章目录 一、String类的重要性二、String类中的常用方法1.字符串构造2.String对象的比较3.字符串查找4.转换5.字符串替换6.字符串拆分7.字符串截取8.其他操作方法9.字符串的不可变性10.字符串修改 三、StringBuilder和StringBuffer 一、String类的重要性 在C语言中已经涉及到…...

算法——滑动窗口(Sliding Window)
一、背景知识 滑动窗口算法(Sliding Window): 在给定数组 / 字符串上维护一个固定长度或不定长度的窗口。可以对窗口进行滑动操作、缩放操作,以及维护最优解操作。题型一:固定长度题型二:不固定长度 二、例…...

Android异步之旅:探索AsyncTask
前言: 在Android应用程序开发中,异步操作是非常常见的需求。比如,我们可能需要在后台线程中执行网络请求、数据库操作或者其他耗时的任务,而不阻塞UI线程。为了实现这些异步操作,Android提供了多种方式,其…...

kibana 7安装
手动安装 下载 wget https://artifacts.elastic.co/downloads/kibana/kibana-7.17.15-linux-x86_64.tar.gz 解压 mv kibana-7.17.15-linux-x86_64.tar.gz /usr/local tar -zxvf kibana-7.17.15-linux-x86_64.tar.gz chown -R es:es kibana-7.17.15-linux-x86_64修改配置 s…...

为何内存不够用?微服务改造启动多个Spring Boot的陷阱与解决方案
在生产环境中我们会遇到一些问题,此文主要记录并复盘一下当时项目中的实际问题及解决过程。 背景简述 最初系统上线后都比较正常风平浪静的。在系统运行了一段时间后,业务量上升后,生产上发现java应用内存占用过高,服务器总共64…...

大模型变身双面人:虚假新闻制造机VS假新闻鉴别大师!
大家是怎样看待大型语言模型生成信息的可靠性呢? 尽管大语言模型生成的内容“像模像样”,但这些模型偶尔的失误揭示了一个关键问题:它们生成的内容并不总是真实可靠的。 那么,这种“不保真”特性能否被用来制造虚假信息呢&#x…...
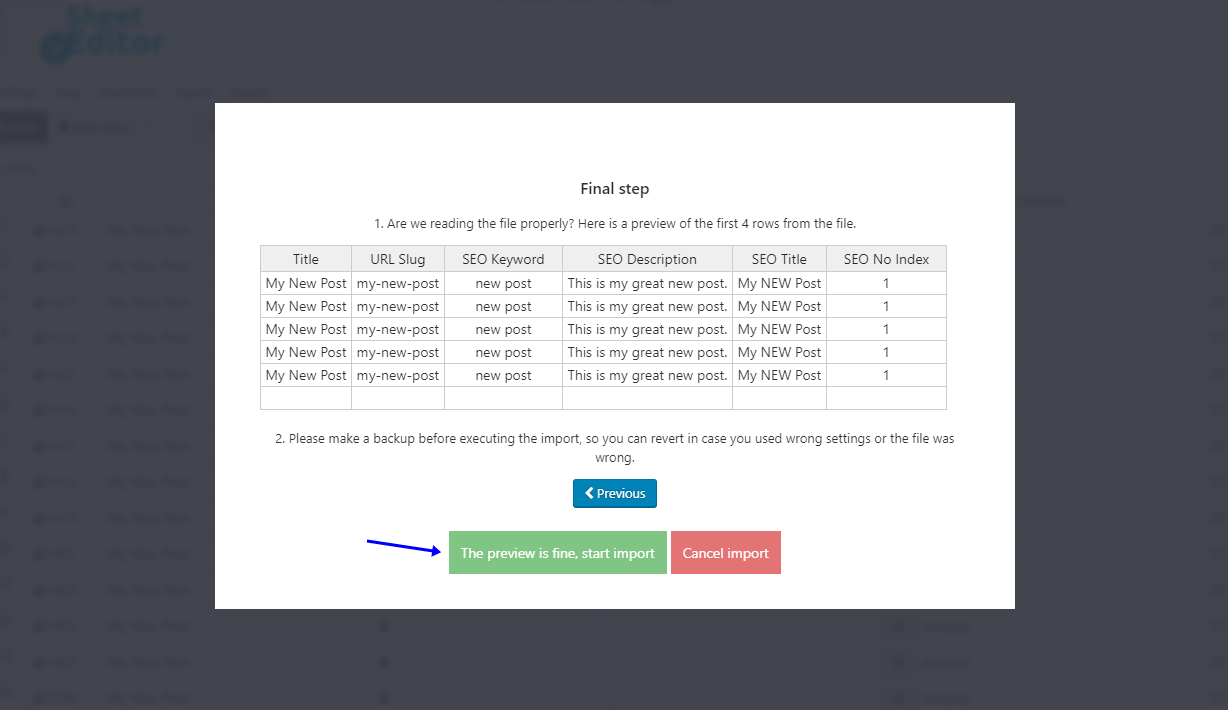
WordPress网站如何修复数千个帖子的SEO错误
在本教程中,我们将向您展示如何解决您经常犯的SEO错误。 最好的是您不必花费太多时间,因为您不需要打开并编辑每个帖子。 相反,我们将向您展示如何使用 WordPress 内的电子表格来修复 WordPress 帖子的 SEO。 在这里,我们为您提…...

Mac如何搭建Vue项目
目录 一、安装node 二、安装NPM 1、本地安装和全局安装 2、通过Node.js官方安装程序安装 3、通过Homebrew安装 三、NPM常用命令 1、查看模块的版本号 2、安装指定版本 3、卸载模块 4、更新模块 5、查看模块信息 6、查看模块地址 7、更新命令 8、卸载NPM 四、安装…...

深入 Django 的 URL 分发器
概要 在 Django 的 MVC 架构中,URL 分发器扮演着至关重要的角色,它负责将用户的请求路由到相应的视图函数或类。这一机制不仅保证了 Django 应用的高度可扩展性,还为开发者提供了灵活的 URL 设计能力。本文将详细介绍 Django 中的 URL 分发器…...

基于单片机设计的气压与海拔高度检测计(采用MPL3115A2芯片实现)
一、前言 随着科技的不断发展,在许多领域中,对气压与海拔高度的测量变得越来越重要。例如,对于航空和航天工业、气象预报、气候研究等领域,都需要高精度、可靠的气压与海拔高度检测装置。针对这一需求,基于单片机设计…...
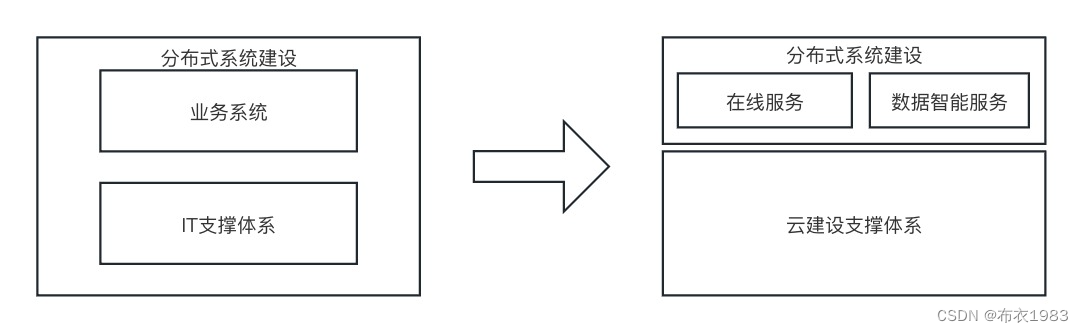
云原生入门系列(背景和驱动力)
做任何一件事,或者学习、应用一个领域的技术,莫过于先要想好阶段的目标和理解、学习它的意义是什么?解决了什么问题? 这部分,就尝试来探讨下这个阶段需要理解并达成的目标以及践行云原生的意义在哪里。 1.历程 任何阶…...

Django中间件
目录 一.介绍 1.什么是Django中间件 2.作用: 3.示例 二.Django请求生命周期流程图 三.Django中间件是Django的门户 四.中间件方法 1.必须掌握的中间件方法 (1)process_request: 示例: 2.需要了解的中间件方法 &#x…...
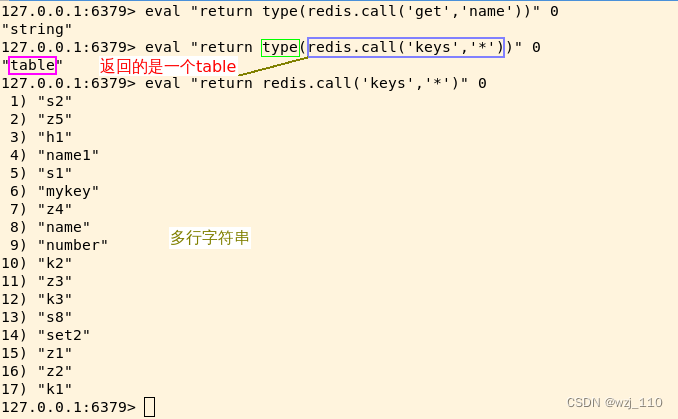
redis运维(十九)redis 的扩展应用 lua(一)
一 redis 的扩展应用 lua redis如何保证原子操作 说明:引入lua脚本,核心解决原子性问题 ① redis为什么引入lua? lua脚本本身体积小,启动速度快 ② redis引入lua的优势 小结: 类似自定义redis命令 ③ redis中如何使用lua ④ EVAL 说明&#…...

SpringBoot——MVC原理
优质博文:IT-BLOG-CN 一、SpringMVC自动配置 SpringMVC auto-configuration:SpringBoot自动配置好了SpringMVC。以下是SpringBoot对SpringMVC的默认配置:[WebMvcAutoConfiguration] 【1】包括ContentNegotiatingViewResolver和BeanNameView…...

[Linux] shell条件语句和if语句
一、条件语句 1.1 测试 test 测试文件的表达式是否成立 格式:test 条件表达式 [ 条件表达式 ] 选项作用-d测试是否为目录-e测试目录或文件是否存在-a测试目录或文件是否存在-f测试是否为文件-r测试当前用户是否有权限读取-w测试当前用户是否有权限写入-x测试当前…...

【陈老板赠书活动 - 18期】-如何成为架构师这几本书推荐给你
陈老老老板🦸 👨💻本文专栏:赠书活动专栏(为大家争取的福利,免费送书) 👨💻本文简述:生活就像海洋,只有意志坚强的人,才能到达彼岸。 👨&am…...

测试微信模版消息推送
进入“开发接口管理”--“公众平台测试账号”,无需申请公众账号、可在测试账号中体验并测试微信公众平台所有高级接口。 获取access_token: 自定义模版消息: 关注测试号:扫二维码关注测试号。 发送模版消息: import requests da…...

业务系统对接大模型的基础方案:架构设计与关键步骤
业务系统对接大模型:架构设计与关键步骤 在当今数字化转型的浪潮中,大语言模型(LLM)已成为企业提升业务效率和创新能力的关键技术之一。将大模型集成到业务系统中,不仅可以优化用户体验,还能为业务决策提供…...

【JVM】- 内存结构
引言 JVM:Java Virtual Machine 定义:Java虚拟机,Java二进制字节码的运行环境好处: 一次编写,到处运行自动内存管理,垃圾回收的功能数组下标越界检查(会抛异常,不会覆盖到其他代码…...

系统设计 --- MongoDB亿级数据查询优化策略
系统设计 --- MongoDB亿级数据查询分表策略 背景Solution --- 分表 背景 使用audit log实现Audi Trail功能 Audit Trail范围: 六个月数据量: 每秒5-7条audi log,共计7千万 – 1亿条数据需要实现全文检索按照时间倒序因为license问题,不能使用ELK只能使用…...

DIY|Mac 搭建 ESP-IDF 开发环境及编译小智 AI
前一阵子在百度 AI 开发者大会上,看到基于小智 AI DIY 玩具的演示,感觉有点意思,想着自己也来试试。 如果只是想烧录现成的固件,乐鑫官方除了提供了 Windows 版本的 Flash 下载工具 之外,还提供了基于网页版的 ESP LA…...

3403. 从盒子中找出字典序最大的字符串 I
3403. 从盒子中找出字典序最大的字符串 I 题目链接:3403. 从盒子中找出字典序最大的字符串 I 代码如下: class Solution { public:string answerString(string word, int numFriends) {if (numFriends 1) {return word;}string res;for (int i 0;i &…...

【论文阅读28】-CNN-BiLSTM-Attention-(2024)
本文把滑坡位移序列拆开、筛优质因子,再用 CNN-BiLSTM-Attention 来动态预测每个子序列,最后重构出总位移,预测效果超越传统模型。 文章目录 1 引言2 方法2.1 位移时间序列加性模型2.2 变分模态分解 (VMD) 具体步骤2.3.1 样本熵(S…...
 自用)
css3笔记 (1) 自用
outline: none 用于移除元素获得焦点时默认的轮廓线 broder:0 用于移除边框 font-size:0 用于设置字体不显示 list-style: none 消除<li> 标签默认样式 margin: xx auto 版心居中 width:100% 通栏 vertical-align 作用于行内元素 / 表格单元格ÿ…...

在WSL2的Ubuntu镜像中安装Docker
Docker官网链接: https://docs.docker.com/engine/install/ubuntu/ 1、运行以下命令卸载所有冲突的软件包: for pkg in docker.io docker-doc docker-compose docker-compose-v2 podman-docker containerd runc; do sudo apt-get remove $pkg; done2、设置Docker…...

腾讯云V3签名
想要接入腾讯云的Api,必然先按其文档计算出所要求的签名。 之前也调用过腾讯云的接口,但总是卡在签名这一步,最后放弃选择SDK,这次终于自己代码实现。 可能腾讯云翻新了接口文档,现在阅读起来,清晰了很多&…...
