(二分查找)leetcode162. 寻找峰值
文章目录
- 一、题目
- 1、题目描述
- 2、基础框架
- 3、原题链接
- 二、解题报告
- 1、思路分析
- 2、时间复杂度
- 3、代码详解
- 三、本题小知识
一、题目
1、题目描述
峰值元素是指其值严格大于左右相邻值的元素。
给你一个整数数组 nums,找到峰值元素并返回其索引。数组可能包含多个峰值,在这种情况下,返回 任何一个峰值 所在位置即可。
你可以假设 nums[-1] = nums[n] = -∞ 。
你必须实现时间复杂度为 O(log n) 的算法来解决此问题。
示例 1:
输入:nums = [1,2,3,1]
输出:2
解释:3 是峰值元素,你的函数应该返回其索引 2。
示例 2:
输入:nums = [1,2,1,3,5,6,4]
输出:1 或 5
解释:你的函数可以返回索引 1,其峰值元素为 2;
或者返回索引 5, 其峰值元素为 6。
2、基础框架
- C++版本给出的基础框架如下:
3、原题链接
https://leetcode.cn/problems/find-peak-element/
二、解题报告
1、思路分析
(1)(1)(1)易证,如果nums[i] > nums[i+1]那么[0…i]区间内肯定存在峰值。如果nums[i] < nums[i+1],那么[i…nums.length-1]区间内肯定存在峰值。
(2)(2)(2)所以该问题具有二分性,如果是nums[mid]>nums[mid+1],那么丢弃[i+1…r],即r = mid.
(3)(3)(3)如果nums[mid]<nums[mid+1],那么就丢弃[l…i],即l = mid +1
(4)(4)(4)二分的出口条件是l >= r,即l一旦等于r就会结束循环,所以mid不会大于r,即mid+1不会有越界问题。
2、时间复杂度
时间复杂度为O(logn)
3、代码详解
class Solution {
public:int findPeakElement(vector<int>& nums) {int l = 0;int r = nums.size() - 1;while(l < r) {int mid = l + (r - l) / 2;if (nums[mid] > nums[mid+1]) {r = mid;}else l = mid + 1;}return r;}
};
三、本题小知识
相关文章:
leetcode162. 寻找峰值)
(二分查找)leetcode162. 寻找峰值
文章目录一、题目1、题目描述2、基础框架3、原题链接二、解题报告1、思路分析2、时间复杂度3、代码详解三、本题小知识一、题目 1、题目描述 峰值元素是指其值严格大于左右相邻值的元素。 给你一个整数数组 nums,找到峰值元素并返回其索引。数组可能包含多个峰值…...
spring boot 配合element ui vue实现表格的批量删除(前后端详细教学,简单易懂,有手就行)
目录 一.前言: 二. 前端代码: 2.1.element ui组件代码 2.2删除按钮 2.3.data 2.4.methods 三.后端代码: 一.前言: 研究了其他人的博客,找到了一篇有含金量的,进行了部分改写实现前后端分离࿰…...
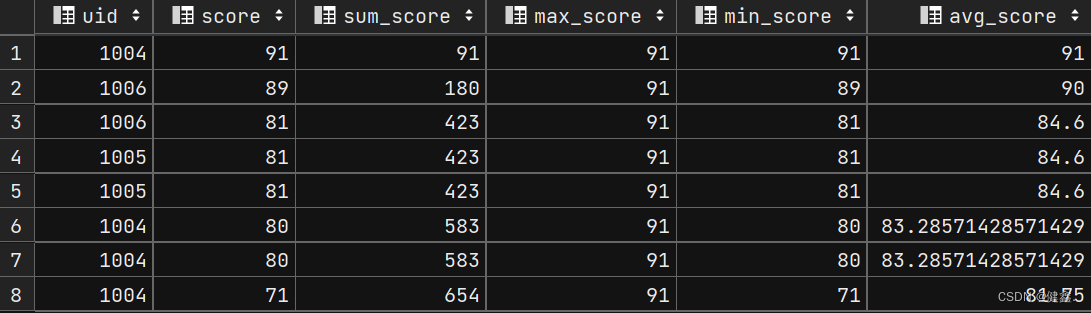
hiveSQL开窗函数详解
hive开窗函数 文章目录hive开窗函数1. 开窗函数概述1.1 窗口函数分类1.2 窗口函数和普通聚合函数的区别2. 窗口函数的基本用法2.1 基本用法2.2 设置窗口的方法2.2.1 window_name2.2.2 partition by2.2.3 order by 子句2.2.4 rows指定窗口大小窗口框架2.3 开窗函数中加 order by…...

深度学习基础实例与总结
一、神经网络 1 深度学习 1 什么是深度学习? 简单来说,深度学习就是一种包括多个隐含层 (越多即为越深)的多层感知机。它通过组合低层特征,形成更为抽象的高层表示,用以描述被识别对象的高级属性类别或特征。 能自生成数据的中…...

在 WIndows 下安装 Apache Tinkerpop (Gremlin)
一、安装 JDK 首先安装 Java JDK,这个去官网下载即可,我下载安装的 JDK19(jdk-19_windows-x64_bin.msi),细节不赘述。 二、去 Tinkerpop 网站下载 Gremlin 网址:https://tinkerpop.apache.org/ 点击下面…...

从软件的角度看待PCI和PCIE(一)
1.最容易访问的设备是什么? 是内存! 要读写内存,知道它的地址就可以了,不需要什么驱动程序; volatile unsigned int *p 0xffff8811; unsigned int val; *p val; val *p;只有内存能这样简单、方便的使用吗…...

DSP_TMS320F28377D_ADC学习笔记
前言 DSP各种模块的使用,基本上就是 GPIO复用配置、相关控制寄存器的配置、中断的配置。本文主要记录本人对ADC模块的学习笔记。TMS320F28377D上面有24路ADC专用IO,这意味着不需要进行GPIO复用配置。 只需要考虑相关控制寄存器和中断的配置。看代码请直…...
springcloud3 Nacos中namespace和group,dataId的联系
一 Namespance和group和dataId的联系 1.1 3者之间的联系 话不多说,上答案,如下图: namespance用于区分部署环境,group和dataId用于逻辑上区分两个目标对象。 二 案例:实现读取注册中心的不同环境下的配置文件 …...
[YOLO] yolo理解博客笔记
YOLO v2和V3 关于设置生成anchorbox,Boundingbox边框回归的过程详细解读 YOLO v2和V3 关于设置生成anchorbox,Boundingbox边框回归的个人理解https://blog.csdn.net/shenkunchang1877/article/details/105648111YOLO v1网络结构计算 Yolov1-pytorch版 …...

清华源pip安装Python第三方包
一、更换PIP源PIP源在国外,速度慢,可以更换为国内源,以下是国内一些常用的PIP源。豆瓣(douban) http://pypi.douban.com/simple/ (推荐)清华大学 https://pypi.tuna.tsinghua.edu.cn/simple/阿里云 http://mirrors.aliyun.com/pypi/simple/中…...

python线程池【ThreadPoolExecutor()】批量获取博客园标题数据
转载:蚂蚁学python 网址:【【2021最新版】Python 并发编程实战,用多线程、多进程、多协程加速程序运行】 https://www.bilibili.com/video/BV1bK411A7tV/?p8&share_sourcecopy_web&vd_sourced0ef3d08fdeef1740bab49cdb3e96467实战案…...
LearnOpenGL-入门-8.坐标系统
本人刚学OpenGL不久且自学,文中定有代码、术语等错误,欢迎指正 我写的项目地址:https://github.com/liujianjie/LearnOpenGLProject LearnOpenGL中文官网:https://learnopengl-cn.github.io/ 文章目录坐标系统概述局部空间世界空…...

windows10使用wsl2安装docker
配环境很麻烦,想利用docker的镜像环境跑一下代码整个安装过程的原理是:windows使用docker,必须先安装一个linux虚拟机,才可运行docker,而采用wsl2安装虚拟机是目前最好的方法第一步 windows安装wsl2控制面板->程序-…...

Javascript的API基本内容(六)
一、正则表达式 1.定义规则 const reg /表达式/ 其中/ /是正则表达式字面量正则表达式也是对象 2.使用正则 test()方法 用来查看正则表达式与指定的字符串是否匹配如果正则表达式与指定的字符串匹配 ,返回true,否则false 3.元字符 比如࿰…...

电压放大器和电流放大器的区别是什么意思
在日常电子实验测试中,很多电子工程师都会使用到电压放大器和电流放大器,但是很多新手工程师却无法区分两者的区别,下面就让安泰电子来为我们讲解电压放大器和电流放大器的区别是什么意思。 一、电压放大器介绍: 电压放大器是一种…...

cast提前!最简单有效的神经网络优化方法,没有之一!
做优化有时候真的很头疼,绞尽脑汁的想怎么做算法等价,怎么把神经网络各层指令流水起来,在确保整网精度的同时,又有高性能。 但有时做了半天,却发现流水根本就流不起来,总是莫名其妙地被卡住。 真的是一顿…...
)
LeetCode刷题——动态规划(C/C++)
文章目录[简单]买股票的最佳时机[简单]爬楼梯[中等]最长递增子序列[中等]最大连续子数组和[简单]买股票的最佳时机 原题链接 题解 min:今天之前买股的最低价 res:最大利润 每一天比较今天和往前的最低价差值能否比最大利润还大 class Solution { publ…...

车载智能终端TBOX
YD886 终端设备是基于GSM/WCDMA全网通讯方式的GPS定位移动终端,车载设备具有强大的车辆监控管理、CAN总线数据采集等功能,可以满足不同用户的需求,同时具备汽车行驶记录功能扩展应用。具体功能请以终端实际情况为准! 一、移动管家 车载智能终…...
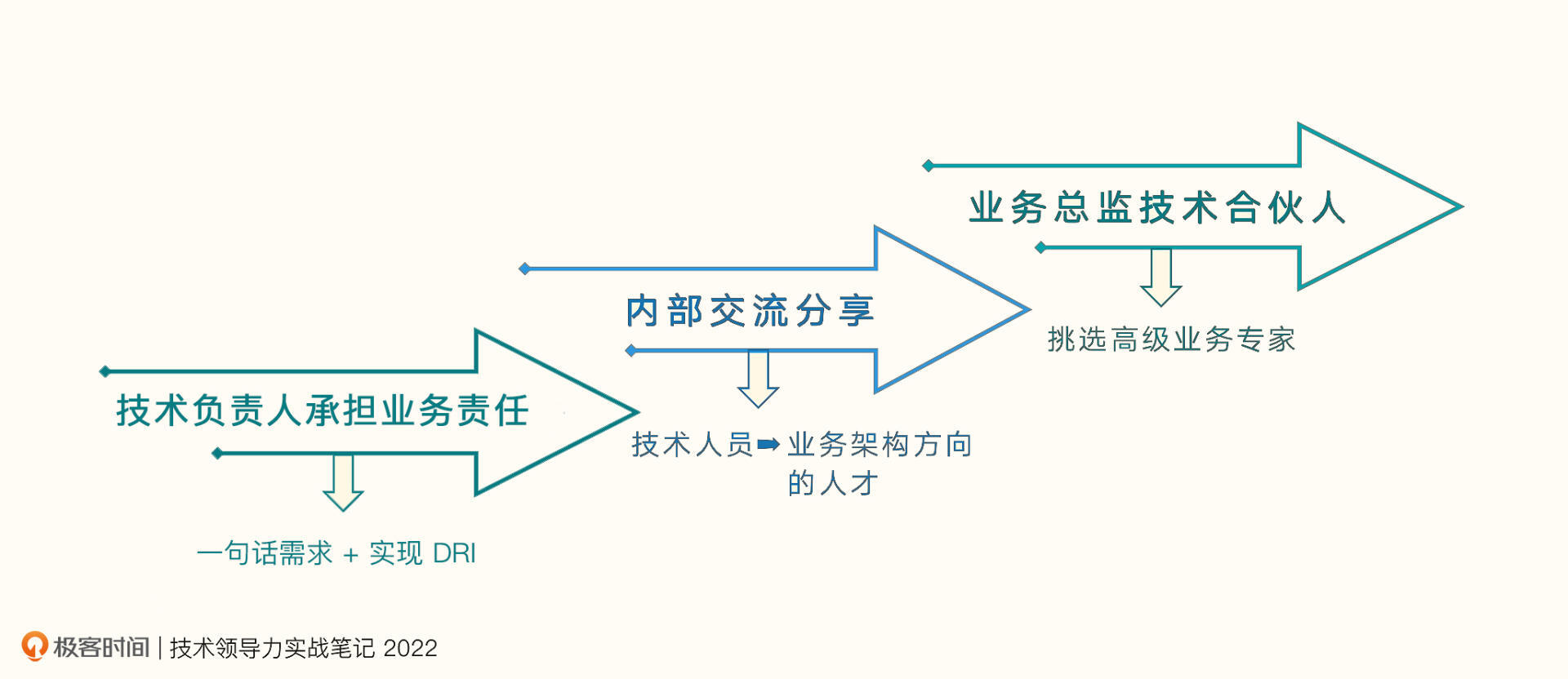
技术分担产品之忧(上):挑选有业务专家潜力的人
你好,我是王植萌,去哪儿网的高级技术总监、TC主席。从2014年起,担任一个部门的技术负责人,有8年技术总监经验、5年TC主席的经验。这节课我会从去哪儿网产研融合的经验出发,和你聊一聊怎么让技术分担产品之忧。 技术分…...
 树上机器人规划(简单版) BFS 二进制)
UVa 12569 Planning mobile robot on Tree (EASY Version) 树上机器人规划(简单版) BFS 二进制
题目链接:Planning mobile robot on Tree (EASY Version) 题目描述: 给定一棵树,树上有一个位置存在一个机器人,其他mmm个位置存在石头,保证初始状态一个结点最多一个物体(一个石头或者一个机器人或者为空…...

C++实现分布式网络通信框架RPC(3)--rpc调用端
目录 一、前言 二、UserServiceRpc_Stub 三、 CallMethod方法的重写 头文件 实现 四、rpc调用端的调用 实现 五、 google::protobuf::RpcController *controller 头文件 实现 六、总结 一、前言 在前边的文章中,我们已经大致实现了rpc服务端的各项功能代…...

抖音增长新引擎:品融电商,一站式全案代运营领跑者
抖音增长新引擎:品融电商,一站式全案代运营领跑者 在抖音这个日活超7亿的流量汪洋中,品牌如何破浪前行?自建团队成本高、效果难控;碎片化运营又难成合力——这正是许多企业面临的增长困局。品融电商以「抖音全案代运营…...

Qt Http Server模块功能及架构
Qt Http Server 是 Qt 6.0 中引入的一个新模块,它提供了一个轻量级的 HTTP 服务器实现,主要用于构建基于 HTTP 的应用程序和服务。 功能介绍: 主要功能 HTTP服务器功能: 支持 HTTP/1.1 协议 简单的请求/响应处理模型 支持 GET…...

从零实现STL哈希容器:unordered_map/unordered_set封装详解
本篇文章是对C学习的STL哈希容器自主实现部分的学习分享 希望也能为你带来些帮助~ 那咱们废话不多说,直接开始吧! 一、源码结构分析 1. SGISTL30实现剖析 // hash_set核心结构 template <class Value, class HashFcn, ...> class hash_set {ty…...

C# SqlSugar:依赖注入与仓储模式实践
C# SqlSugar:依赖注入与仓储模式实践 在 C# 的应用开发中,数据库操作是必不可少的环节。为了让数据访问层更加简洁、高效且易于维护,许多开发者会选择成熟的 ORM(对象关系映射)框架,SqlSugar 就是其中备受…...

什么?连接服务器也能可视化显示界面?:基于X11 Forwarding + CentOS + MobaXterm实战指南
文章目录 什么是X11?环境准备实战步骤1️⃣ 服务器端配置(CentOS)2️⃣ 客户端配置(MobaXterm)3️⃣ 验证X11 Forwarding4️⃣ 运行自定义GUI程序(Python示例)5️⃣ 成功效果
python执行测试用例,allure报乱码且未成功生成报告
allure执行测试用例时显示乱码:‘allure’ �����ڲ����ⲿ���Ҳ���ǿ�&am…...

微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据
微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据 Power Query 具有大量专门帮助您清理和准备数据以供分析的功能。 您将了解如何简化复杂模型、更改数据类型、重命名对象和透视数据。 您还将了解如何分析列,以便知晓哪些列包含有价值的数据,…...
)
Android第十三次面试总结(四大 组件基础)
Activity生命周期和四大启动模式详解 一、Activity 生命周期 Activity 的生命周期由一系列回调方法组成,用于管理其创建、可见性、焦点和销毁过程。以下是核心方法及其调用时机: onCreate() 调用时机:Activity 首次创建时调用。…...

return this;返回的是谁
一个审批系统的示例来演示责任链模式的实现。假设公司需要处理不同金额的采购申请,不同级别的经理有不同的审批权限: // 抽象处理者:审批者 abstract class Approver {protected Approver successor; // 下一个处理者// 设置下一个处理者pub…...
