最小二乘线性回归
线性回归(linear regression):试图学得一个线性模型以尽可能准确地预测实际值的输出。
以一个例子来说明线性回归,假设银行贷款会根据 年龄 和 工资 来评估可放款的额度。即:
数据:工资和年龄(2个特征)
目标:预测银行放款额度(标签)
参数:考虑工资和年龄分别对放款额度的影响程度
可以写成这样: Y = X 1 θ 1 + X 2 θ 2 Y=X_1\theta_1+X_2\theta_2 Y=X1θ1+X2θ2,这里 X 1 、 X 2 就是特征, Y X_1、X_2 就是特征,Y X1、X2就是特征,Y就是银行最终放款额度。
找到最合适的一个平面来拟合数据点:

拟合的平面方程: h θ ( x ) = θ 0 + θ 1 x 1 + θ 2 x 2 h_{\theta}(x)=\theta_0+\theta_1x_1+\theta_2x_2 hθ(x)=θ0+θ1x1+θ2x2,这里 θ 0 \theta_0 θ0是偏置项。整合该方程可以写成如下形式:
h θ ( x ) = ∑ i = 0 n θ i x i = θ ⊤ x h_{\theta}(x)=\sum_{i=0}^n \theta_ix_i=\theta^\top x hθ(x)=i=0∑nθixi=θ⊤x
注意这里 x 0 = 1 x_0=1 x0=1,添加一个全为1的特征,方便表示。
真实值和预测值之间肯定存在误差,用 ϵ \epsilon ϵ来表示误差。对于每个样本:
y i = θ ⊤ x i + ϵ i y_i = \theta^\top x_i + \epsilon_i yi=θ⊤xi+ϵi
这里 y i y_i yi 为真实值, θ ⊤ x i \theta^\top x_i θ⊤xi为预测值, ϵ i \epsilon_i ϵi为误差项
对于误差的理解:误差 ϵ i \epsilon_i ϵi是独立同分布的,且服从均值为0方差为 θ 2 \theta^2 θ2的高斯分布
- 独立:每个样本 x i x_i xi是没有关系的(张三李四一起放款,他俩没关系)
- 同分布:每个 x i x_i xi都是对于同一个问题的(他俩都是来同一家银行 )
- 高斯分布:误差可大可小,但是绝大多数情况下这个浮动不会太大,极小情况下浮动会比较大,符合正常情况。
由于误差服从高斯分布:
p ( ϵ i ) = 1 2 π σ e − 1 2 ( ϵ i σ ) 2 p(\epsilon_i) = \frac{1}{\sqrt{2\pi}\sigma } e^{-\frac{1}{2}\left(\frac{\epsilon_i}{\sigma}\right)^2} p(ϵi)=2πσ1e−21(σϵi)2
将预测值和误差带入上式得:
y i = θ ⊤ x i + ϵ i 带入 p ( ϵ i ) = 1 2 π σ e − 1 2 ( ϵ i σ ) 2 : p ( y i ∣ x i ; θ ) = 1 2 π σ e − 1 2 ( y i − θ ⊤ x i σ ) 2 y_i = \theta^\top x_i + \epsilon_i \\ 带入\ \ p(\epsilon_i) = \frac{1}{\sqrt{2\pi}\sigma } e^{-\frac{1}{2}\left(\frac{\epsilon_i}{\sigma}\right)^2}:\\ p(y_i|x_i;\theta)=\frac{1}{\sqrt{2\pi}\sigma } e^{-\frac{1}{2}\left(\frac{y_i-\theta^\top x_i}{\sigma}\right)^2} yi=θ⊤xi+ϵi带入 p(ϵi)=2πσ1e−21(σϵi)2:p(yi∣xi;θ)=2πσ1e−21(σyi−θ⊤xi)2
上式的似然函数如下:
L ( θ ) = ∏ i = 1 m p ( y i ∣ x i ; θ ) = ∏ i = 1 m 1 2 π σ e − 1 2 ( y i − θ ⊤ x i σ ) 2 L(\theta) = \prod_{i=1}^mp(y_i|x_i;\theta)=\prod_{i=1}^m \frac{1}{\sqrt{2\pi}\sigma } e^{-\frac{1}{2}\left(\frac{y_i-\theta^\top x_i}{\sigma}\right)^2} L(θ)=i=1∏mp(yi∣xi;θ)=i=1∏m2πσ1e−21(σyi−θ⊤xi)2
对似然函数的解释:
什么样的参数跟我们的数据组合后恰好是真实值
对数似然:
l o g L ( θ ) = l o g ∏ i = 1 m p ( y i ∣ x i ; θ ) = l o g ∏ i = 1 m 1 2 π σ e − 1 2 ( y i − θ ⊤ x i σ ) 2 = m l o g 1 2 π σ − 1 σ 2 ∗ 1 2 ∗ ∑ i = 1 m ( y i − θ ⊤ x i ) 2 log L(\theta) =log \prod_{i=1}^mp(y_i|x_i;\theta)=log \prod_{i=1}^m \frac{1}{\sqrt{2\pi}\sigma } e^{-\frac{1}{2}\left(\frac{y_i-\theta^\top x_i}{\sigma}\right)^2}\\=mlog\frac{1}{\sqrt{2 \pi}\sigma}-\frac{1}{\sigma ^2}*\frac12*\sum_{i=1}^m(y_i-\theta^\top x_i)^2 logL(θ)=logi=1∏mp(yi∣xi;θ)=logi=1∏m2πσ1e−21(σyi−θ⊤xi)2=mlog2πσ1−σ21∗21∗i=1∑m(yi−θ⊤xi)2
目标是让似然函数(对数变换之后)越大越好:
m a x l o g L ( θ ) → m i n J ( θ ) = 1 2 ∑ i = 1 m ( y i − θ ⊤ x i ) 2 (最小二乘法) max \ log L(\theta)\\ →min \ J(\theta)=\frac12 \sum_{i=1}^m(y_i-\theta^\top x_i)^2(最小二乘法) max logL(θ)→min J(θ)=21i=1∑m(yi−θ⊤xi)2(最小二乘法)
J ( θ ) = 1 2 ∑ i = 1 m ( y i − θ ⊤ x i ) 2 J(\theta)=\frac12 \sum_{i=1}^m(y_i-\theta^\top x_i)^2 J(θ)=21∑i=1m(yi−θ⊤xi)2即为最小二乘法。
将目标函数写为矩阵形式:
J ( θ ) = 1 2 ∑ i = 1 m ( y i − θ ⊤ x i ) 2 = 1 2 ( X θ − y ) ⊤ ( X θ − y ) 对 θ 求偏导 : ∇ θ J ( θ ) = X ⊤ X θ − X ⊤ y 令 ∇ θ J ( θ ) = 0 得 : θ = ( X ⊤ X ) − 1 X ⊤ y J(\theta)=\frac12 \sum_{i=1}^m(y_i-\theta^\top x_i)^2= \frac12(X\theta-y)^\top (X\theta-y)\\ 对\theta 求偏导:\\ \nabla_\theta J(\theta)=X^\top X\theta-X^\top y\\ 令\nabla_\theta J(\theta)=0得:\\ \theta=(X^\top X)^{-1}X^\top y J(θ)=21i=1∑m(yi−θ⊤xi)2=21(Xθ−y)⊤(Xθ−y)对θ求偏导:∇θJ(θ)=X⊤Xθ−X⊤y令∇θJ(θ)=0得:θ=(X⊤X)−1X⊤y
采用微分和迹的关系 d f = t r ( ( ∂ f ∂ X ) ⊤ d X ) df= tr((\frac{\partial f}{\partial X})^\top dX) df=tr((∂X∂f)⊤dX)进行求导,求导过程如下:
d J ( θ ) = t r ( d J ( θ ) ) = d [ 1 2 ( X θ − y ) ⊤ ( X θ − y ) ] = t r [ d ( 1 2 ( θ ⊤ X ⊤ X θ − 2 y ⊤ X θ + y ⊤ y ) ) ] = t r [ d ( 1 2 θ ⊤ X ⊤ X θ ) ] − t r ( d ( 2 y ⊤ X θ ) ) + t r ( d ( y ⊤ y ) ) = t r ( 1 2 d θ ⊤ X ⊤ X θ ) + t r ( 1 2 θ ⊤ X ⊤ X d θ ) − t r ( 2 y ⊤ X d θ ) + 0 = t r ( 1 2 θ ⊤ X ⊤ X d θ ) + t r ( 1 2 θ ⊤ X ⊤ X d θ ) − t r ( 2 y ⊤ X d θ ) = t r ( θ ⊤ X ⊤ X d θ − 2 y ⊤ X d θ ) = t r ( ( θ ⊤ X ⊤ X − 2 y ⊤ X ) d θ ) = t r ( ( X ⊤ X θ − 2 X ⊤ y ) ⊤ d θ ) 故: ∂ J ( θ ) ∂ θ = X ⊤ X θ − 2 X ⊤ y dJ(\theta)= tr(dJ(\theta))=d[\frac12(X\theta-y)^\top (X\theta-y)]\\ =tr[d(\frac12(\theta^\top X^\top X\theta-2y^\top X\theta+y^\top y))]\\ =tr[d(\frac12\theta^\top X^\top X\theta)]-tr(d(2y^\top X\theta))+tr(d(y^\top y))\\ =tr(\frac12d\theta^\top X^\top X\theta)+tr(\frac12\theta^\top X^\top Xd\theta)-tr(2y^\top Xd\theta)+0\\ =tr(\frac12\theta^\top X^\top Xd\theta)+tr(\frac12\theta^\top X^\top Xd\theta)-tr(2y^\top Xd\theta)\\ =tr(\theta^\top X^\top Xd\theta-2y^\top Xd\theta)=tr((\theta^\top X^\top X-2y^\top X)d\theta)\\ =tr(( X^\top X\theta - 2X^\top y)^\top d\theta)\\ 故:\\ \frac{\partial J(\theta)}{\partial \theta}=X^\top X\theta - 2X^\top y\\ dJ(θ)=tr(dJ(θ))=d[21(Xθ−y)⊤(Xθ−y)]=tr[d(21(θ⊤X⊤Xθ−2y⊤Xθ+y⊤y))]=tr[d(21θ⊤X⊤Xθ)]−tr(d(2y⊤Xθ))+tr(d(y⊤y))=tr(21dθ⊤X⊤Xθ)+tr(21θ⊤X⊤Xdθ)−tr(2y⊤Xdθ)+0=tr(21θ⊤X⊤Xdθ)+tr(21θ⊤X⊤Xdθ)−tr(2y⊤Xdθ)=tr(θ⊤X⊤Xdθ−2y⊤Xdθ)=tr((θ⊤X⊤X−2y⊤X)dθ)=tr((X⊤Xθ−2X⊤y)⊤dθ)故:∂θ∂J(θ)=X⊤Xθ−2X⊤y
当 X ⊤ X X^\top X X⊤X为满秩矩阵或者正定矩阵时,令偏导数 ∂ J ( θ ) ∂ θ = X ⊤ X θ − 2 X ⊤ y = 0 \frac{\partial J(\theta)}{\partial \theta}=X^\top X\theta - 2X^\top y=0 ∂θ∂J(θ)=X⊤Xθ−2X⊤y=0得到:
θ = ( X ⊤ X ) − 1 X ⊤ y \theta=(X^\top X)^{-1}X^\top y θ=(X⊤X)−1X⊤y
其中 ( X ⊤ X ) − 1 (X^\top X)^{-1} (X⊤X)−1是矩阵 X ⊤ X X^\top X X⊤X的逆矩阵。但是现实任务中, X ⊤ X X^\top X X⊤X通常不是满秩矩阵,例如在许多任务中会遇到大量的变量,其数目甚至超过样例数,导致X的列数多于行数, X ⊤ X X^\top X X⊤X , X ⊤ X X^\top X X⊤X显然不满秩。此时可以解出多个 θ \theta θ,他们都能使均方差最小化。选择哪一个解作为输出,将由机器学习算法的归纳偏好决定,常见的做法是引入正则化项。
相关文章:

最小二乘线性回归
线性回归(linear regression):试图学得一个线性模型以尽可能准确地预测实际值的输出。 以一个例子来说明线性回归,假设银行贷款会根据 年龄 和 工资 来评估可放款的额度。即: 数据:工资和年龄&…...

【django+vue】连接数据库、登录功能
笔记为自我总结整理的学习笔记,若有错误欢迎指出哟~ 【djangovue专栏】 1.【djangovue】项目搭建、解决跨域访问 【djangovue】连接数据库、登录功能 django连接数据库1.安装MySQL驱动程序2.创建数据库3.配置settings.py文件4.创建表5.添加数据 登录功能1.django实现…...

NX二次开发UF_CSYS_edit_matrix_of_object 函数介绍
文章作者:里海 来源网站:https://blog.csdn.net/WangPaiFeiXingYuan UF_CSYS_edit_matrix_of_object Defined in: uf_csys.h int UF_CSYS_edit_matrix_of_object(tag_t object_id, tag_t matrix_id ) overview 概述 Updates the specified coordinat…...

封装公共el-form表单
1.公共表单组件 //commonForm.vue <script> import {TEXT,SELECT,PASSWORD,TEXTAREA,RADIO,DATE_PICKER } from /conf/uiTypes import { deepClone } from /utils export default {name: GFormCreator,props: {config: { // title/itemstype: Object,required: true}}…...

OpenHarmony-4.0-Release 源码编译记录
本文基于 Ubuntu 20.04.4 LTS 1、环境准备 这个没啥好说的,都是搞机的,用之前编译 aosp 的 linux 环境就行,有小伙伴担心会把之前的环境搞崩, 也有用 docker 编译的,我这里就直接在 aosp 环境下搞了,还省…...

HTML新手入门笔记整理:块元素和行内元素
块元素 在HTML中,块元素在浏览器显示状态下独占一行,并且排斥其他元素与其位于一行。一般情况下,块元素内部可以容纳其他块元素和行内元素。 常见块元素 块元素 说明 h1~h6 标题元素 p 段落元素 div div元素 hr 水平线 ol 有序列…...
Hook+jsdom 解决cookie逆向
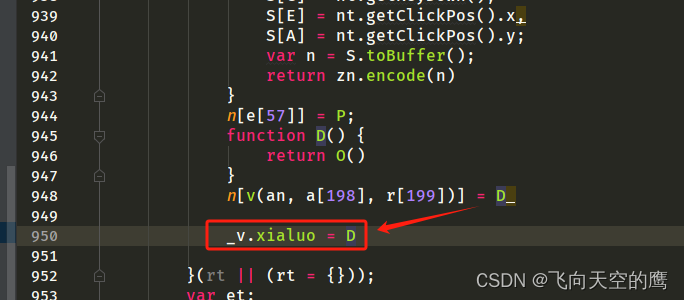
前言 记录下如何破cookie逆向 目标 目标网址:https://q.10jqka.com.cn/ 目标接口:http://q.10jqka.com.cn/index/index/board/all/field/zdf/order/desc/page/2/ajax/1/ 对抗:cookie反爬虫处理,关键字v,如图 解决步骤 1、JS中关键字查找 如上,我们找到了关键字 v,…...

【封装UI组件库系列】封装Icon图标组件
封装UI组件库系列第三篇封装Icon图标组件 🌟前言 🌟封装Icon 1.创建Icon组件 2.引用svg图标库 第一步 第二步 第三步 3.二次封装 4.封装自定义属性 🌟总结 🌟前言 在前端开发中,大家可能已经用过各种各样的UI组…...
STM32:基本定时器原理和定时程序
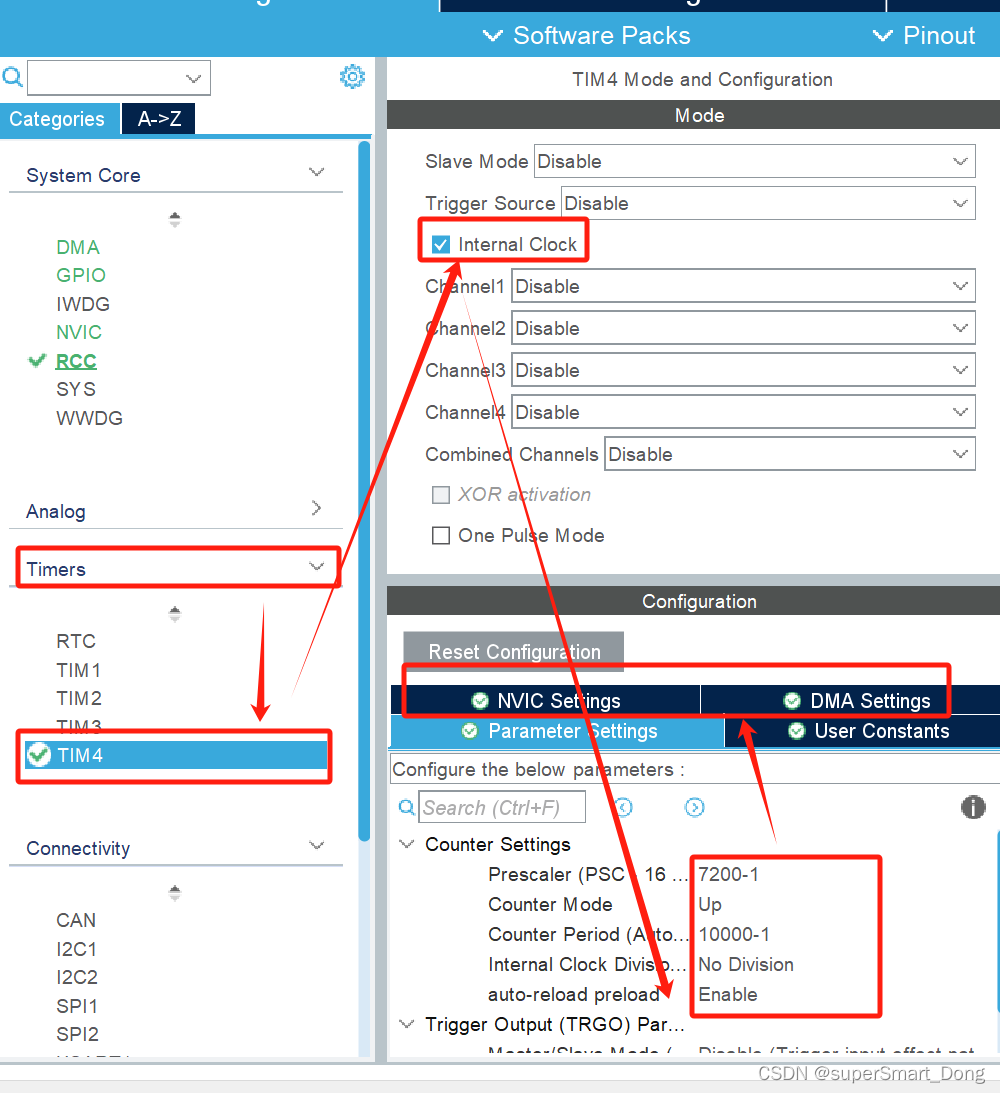
一、初识定时器TIM 定时器就是计数器,定时器的作用就是设置一个时间,然后时间到后就会通过中断等方式通知STM32执行某些程序。定时器除了可以实现普通的定时功能,还可以实现捕获脉冲宽度,计算PWM占空比,输出PWM波形&am…...

EntityFramework 批量删除操作
刚刚开始使用Entityframwork 来操作数据库。遇到了批量删除数据。 EF内部用的方法是:dbcontext.Datas.RemoveRange(list); 这总方法,少量数据是可行的。 但遇到大数据量的时候,这个方法完全不能用。 所以找了另一种方法: stri…...

springboot使用的设计模式
设计模式是在软件设计中常用的一些通用解决方案。在开发商城编码时,以下设计模式可能会有用: 工厂模式(Factory Pattern): 用于创建对象的模式。在商城中,可能会涉及到创建不同类型的商品、订单等对象&…...

IP地址定位技术发展与未来趋势
随着互联网的快速发展,人们对网络的需求和依赖程度越来越高。在海量的网络数据传输中,IP地址定位技术作为网络安全与信息追踪的重要手段,其精准度一直备受关注。近年来,随着技术的不断进步,IP地址定位的精准度得到了显…...

AI与交通运输
人工智能(AI)正在改变几乎所有行业,交通运输也不例外。 虽然与某些行业相比,我们运输货物和乘客的方式在过去 50 年里变化相对较小,但人工智能有望引发一场运输革命—如果你正在寻找人工智能的机会,不要错过…...

window.requestAnimationFrame+localStorage+canvas实现跨窗口小球连线效果
文章目录 前言效果代码后言 前言 hello world欢迎来到前端的新世界 😜当前文章系列专栏:前端系列文章 🐱👓博主在前端领域还有很多知识和技术需要掌握,正在不断努力填补技术短板。(如果出现错误,感谢大家…...

使用AndResGuard报错:copy res file not in resources.arsc file:Ezi.xml
Android使用AndResGuard进行资源混淆,压缩。 源码地址:GitHub - shwenzhang/AndResGuard: proguard resource for Android by wechat team 集成完成后编译过程中出现如下错误: 14:57:05 copy res file not in resources.arsc file:IUk.xml…...

插入排序(形象类比)
最近在看riscv手册的时候,里面有一段代码是插入排序,但是单看代码的时候有点迷,没看懂咋操作的,后来又查资料复习了一下,最终才把代码看明白,所以写篇博客记录一下。 插入排序像打扑克牌 这是我听到过比较形…...

ElasticSearch 同步的方式
ElasticSearch 同步的方式 ElasticSearch是一款强大的分布式搜索和分析引擎,支持多种方式同步数据和日志。下面介绍几种常见的同步方式: 1. Logstash Logstash 是 ElasticStack 的一部分,用于收集、处理和转发日志和事件数据。通过配置 Lo…...

easyExcel实现分批导入,动态表头分批导出,以及导出表格样式设置
<dependency><groupId>com.alibaba</groupId><artifactId>easyexcel</artifactId><version>2.2.6</version></dependency> 一,分批导入 1.首先配置表格头映射类 Getter Setter EqualsAndHashCode public class …...

Android BottomNavigationView底部菜单栏文字显示问题
1. BottomNavigationView 如果tab栏数据小于等于3个,那么图标和文字都是展示出来; 2. BottomNavigationView 如果tab栏数据大于3个,那么图标会显示出来,但是文字会隐藏; 3. 解决方式: (当底部…...
)
从零开始学习typescript——运算符(条件运算法、逻辑运算符、类型运算符、位运算)
条件运算符 条件运算符是一个根据条件返回不同运算结果的运算符 关键字:?: 三元运算符 它可以换成if …else 判断 ? true : false 判断为true,返回?号后面的,判断为false ,返回: 号后面的 逻辑运算符 用…...
)
Java 语言特性(面试系列2)
一、SQL 基础 1. 复杂查询 (1)连接查询(JOIN) 内连接(INNER JOIN):返回两表匹配的记录。 SELECT e.name, d.dept_name FROM employees e INNER JOIN departments d ON e.dept_id d.dept_id; 左…...

基于Flask实现的医疗保险欺诈识别监测模型
基于Flask实现的医疗保险欺诈识别监测模型 项目截图 项目简介 社会医疗保险是国家通过立法形式强制实施,由雇主和个人按一定比例缴纳保险费,建立社会医疗保险基金,支付雇员医疗费用的一种医疗保险制度, 它是促进社会文明和进步的…...

蓝牙 BLE 扫描面试题大全(2):进阶面试题与实战演练
前文覆盖了 BLE 扫描的基础概念与经典问题蓝牙 BLE 扫描面试题大全(1):从基础到实战的深度解析-CSDN博客,但实际面试中,企业更关注候选人对复杂场景的应对能力(如多设备并发扫描、低功耗与高发现率的平衡)和前沿技术的…...

五年级数学知识边界总结思考-下册
目录 一、背景二、过程1.观察物体小学五年级下册“观察物体”知识点详解:由来、作用与意义**一、知识点核心内容****二、知识点的由来:从生活实践到数学抽象****三、知识的作用:解决实际问题的工具****四、学习的意义:培养核心素养…...

页面渲染流程与性能优化
页面渲染流程与性能优化详解(完整版) 一、现代浏览器渲染流程(详细说明) 1. 构建DOM树 浏览器接收到HTML文档后,会逐步解析并构建DOM(Document Object Model)树。具体过程如下: (…...
)
python爬虫:Newspaper3k 的详细使用(好用的新闻网站文章抓取和解析的Python库)
更多内容请见: 爬虫和逆向教程-专栏介绍和目录 文章目录 一、Newspaper3k 概述1.1 Newspaper3k 介绍1.2 主要功能1.3 典型应用场景1.4 安装二、基本用法2.2 提取单篇文章的内容2.2 处理多篇文档三、高级选项3.1 自定义配置3.2 分析文章情感四、实战案例4.1 构建新闻摘要聚合器…...

稳定币的深度剖析与展望
一、引言 在当今数字化浪潮席卷全球的时代,加密货币作为一种新兴的金融现象,正以前所未有的速度改变着我们对传统货币和金融体系的认知。然而,加密货币市场的高度波动性却成为了其广泛应用和普及的一大障碍。在这样的背景下,稳定…...

如何在网页里填写 PDF 表格?
有时候,你可能希望用户能在你的网站上填写 PDF 表单。然而,这件事并不简单,因为 PDF 并不是一种原生的网页格式。虽然浏览器可以显示 PDF 文件,但原生并不支持编辑或填写它们。更糟的是,如果你想收集表单数据ÿ…...

Springboot社区养老保险系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,社区养老保险系统小程序被用户普遍使用,为方…...

Fabric V2.5 通用溯源系统——增加图片上传与下载功能
fabric-trace项目在发布一年后,部署量已突破1000次,为支持更多场景,现新增支持图片信息上链,本文对图片上传、下载功能代码进行梳理,包含智能合约、后端、前端部分。 一、智能合约修改 为了增加图片信息上链溯源,需要对底层数据结构进行修改,在此对智能合约中的农产品数…...
