【C++】二叉搜索树的模拟实现
一、概念
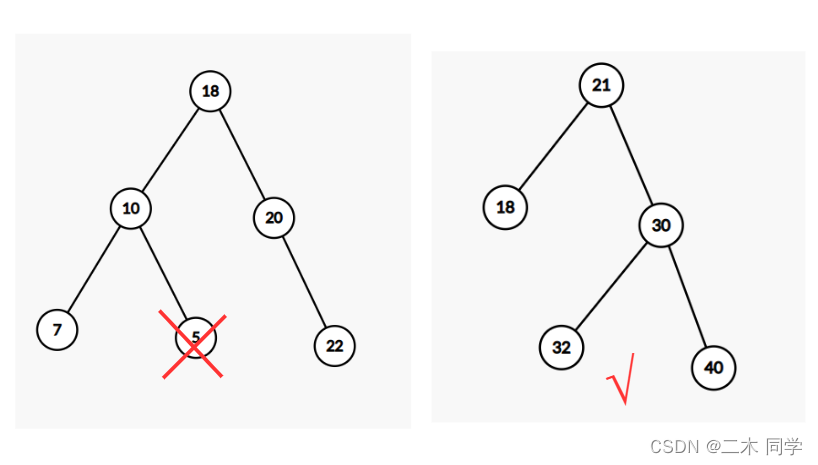
二叉搜索树又称二叉排序树,它或者是一棵空树,或者是具有以下性质的二叉树:
- 若它的左子树不为空,则左子树上所有节点的值都小于根节点的值
- 若它的右子树不为空,则右子树上所有节点的值都大于根节点的值
- 它的左右子树也分别为二叉搜索树
二、二叉搜索树的操作
1. 查找
- 从根开始比较,查找,比根大则往右边走查找,比根小则往左边走查找
- 最多查找高度次,走到空,还没找到,这个值不存在
2. 插入
插入的具体过程如下:
- 树为空,则直接新增节点,赋值给root指针
- 树不空,按二叉搜索树性质查找插入位置,插入新节点
3. 删除
首先查找元素是否在二叉搜索树中,如果不存在,则直接返回;
否则要删除的结点可能分下面四种情况:
a. 要删除的结点无孩子结点
b. 要删除的结点只有左孩子结点
c. 要删除的结点只有右孩子结点
d. 要删除的结点有左、右孩子结点
情况a可以与情况b或者c合并起来,因此真正的删除过程如下:
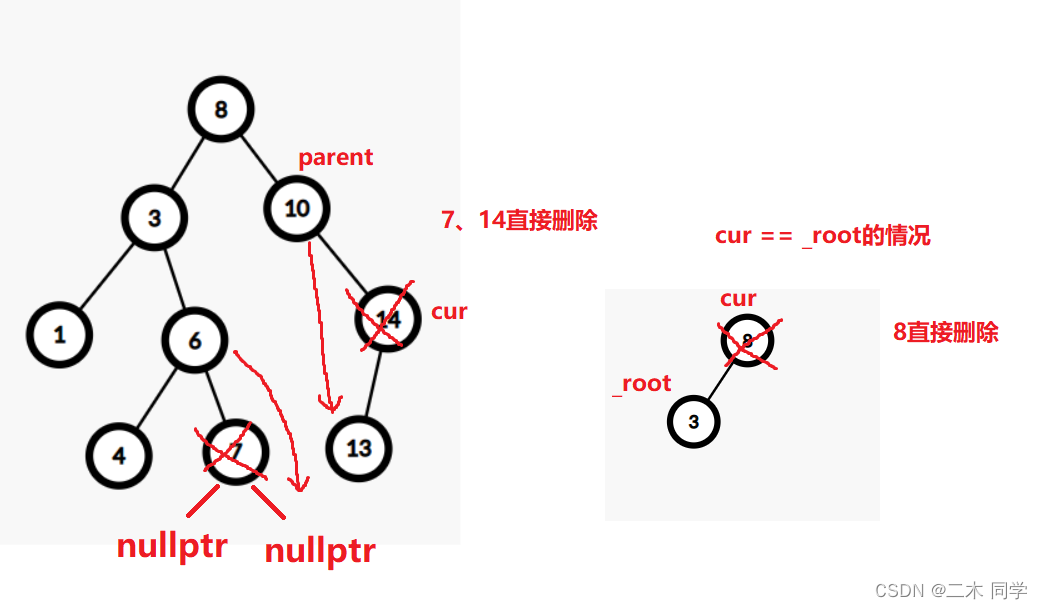
- 情况b:删除该结点且使被删除节点的双亲结点指向被删除节点的左孩子结点–直接删除
- 情况c:删除该结点且使被删除节点的双亲结点指向被删除结点的右孩子结点–直接删除
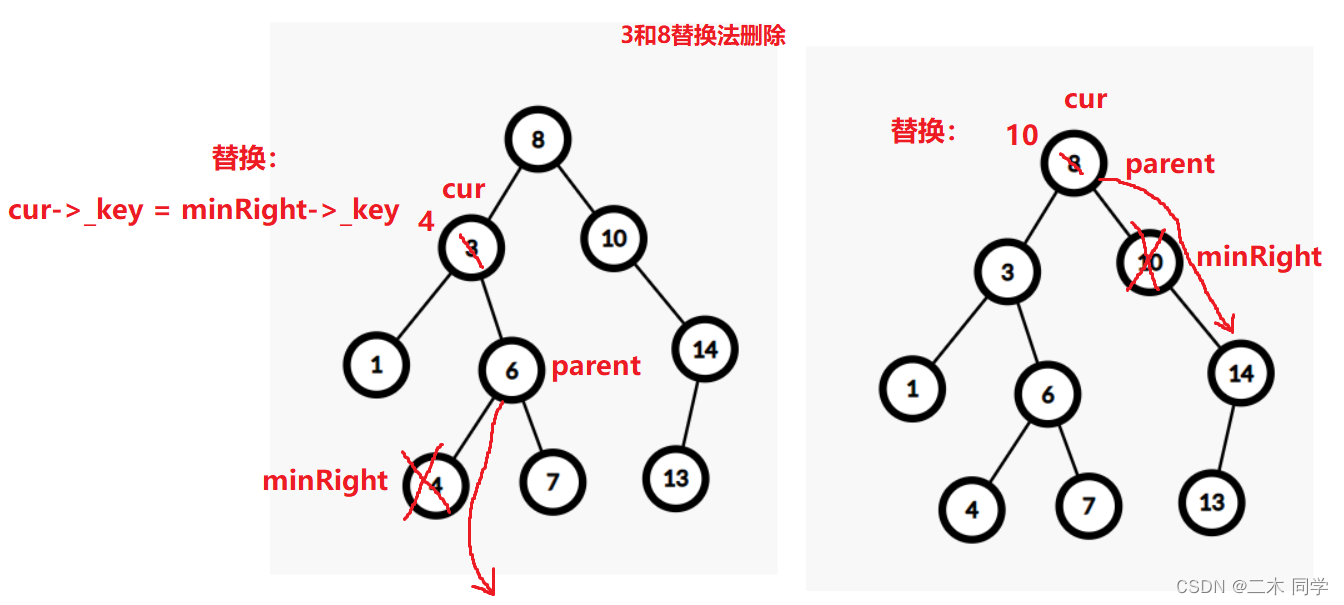
- 情况d:在它的右子树中寻找中序下的第一个结点(关键码在右子树中最小),用它的值填补到被删除节点中,再来处理该结点的删除问题–替换法删除
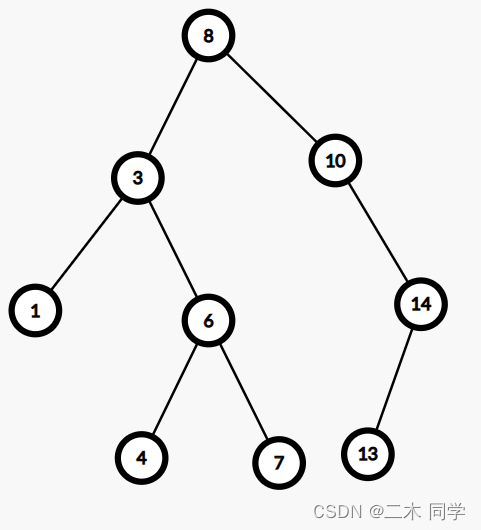
依次删除上图的7、14、3、8
7、14属于直接删除的场景
3、8属于需要替换法进行删除的场景
三、二叉搜索树的实现
1. 基本框架
namespace K
{template<class K>struct BSTreeNode //树的节点{BSTreeNode<K>* _left;BSTreeNode<K>* _right;K _key;BSTreeNode(const K& key):_left(nullptr),_right(nullptr),_key(key){}};template<class K>class BSTree{typedef BSTreeNode<K> Node;public:BSTree():_root(nullptr){}//……各种函数private:Node* _root;};
}
2. 构造和析构
namespace nb
{//……template<class K>class BSTree{typedef BSTreeNode<K> Node;public:BSTree():_root(nullptr){}BSTree(const BSTree<K>& tree){_root = Copy(tree._root);}~BSTree(){Destroy(_root);}private:Node* Copy(Node* root){if (root == nullptr) return nullptr;//前序构建树Node* newRoot = new Node(root->_k);newRoot->_left = Copy(root->_left);newRoot->_right = Copy(root->_right);return newRoot;}void Destroy(Node* root){if (root == nullptr) return;//后序销毁树Destroy(root->_left);Destroy(root->_right);delete root;}private:Node* _root;};
}
3. 查找
实现可以使用迭代,也可以使用递归。
递归版本需要写一个子函数,因为类外部是不能直接访问私有成员变量_root的
bool Find(const K& key)
{Node* cur = _root;while (cur){if (key > cur->_key){//大了往右边查找cur = cur->_right;}else if (key < cur->_key){//小了往左边查找cur = cur->_left;}else{//查找到了return true;}}//没有查找到return false;
}
//递归版
bool FindR(const K& key)
{return _FindR(_root, key);
}
bool _FindR(Node* root, const K& key)
{if (root == nullptr)return false;if (key < root->_key)return _FindR(root->_left, key);else if (key > root->_key)return _FindR(root->_right, key);elsereturn true;
}
4. 插入
bool Insert(const K& key)
{//是空树,直接赋值if (_root == nullptr){_root = new Node(key);return true;}//不是空树,找到对应位置在插入Node* cur = _root;Node* parent = nullptr;//记录双亲节点,用于链接newNodewhile (cur){if (key > cur->_key){parent = cur;cur = cur->_right;}else if (key < cur->_key){parent = cur;cur = cur->_left;}else{//树中已经有该key,则不插入return false;}}cur = new Node(key);//key大了往右边插,小了往左边插if (cur->_key > parent->_key){parent->_right = cur;}else{parent->_left = cur;}return true;
}
//递归版
bool InsertR(const K& key)
{return _InsertR(_root, key);
}
//注意root传引用
bool _InsertR(Node*& root, const K& key)
{//走到空时插入,此时的root是上一次根的左指针或右指针的引用if (root == nullptr){root = new Node(key);return true;}//key大了往右边走,小了往左边走if (key > root->_key){return _InsertR(root->_right, key);}else if (key < root->_key){return _InsertR(root->_left, key);}else{return false;}
}
5. 删除
- 直接删除:
- 替换法删除:
bool Erase(const K& key)
{Node* parent = nullptr;Node* cur = _root;while (cur){if (key > cur->_key){parent = cur;cur = cur->_right;}else if (key < cur->_key){parent = cur;cur = cur->_left;}else // 找到相等节点开始删除操作{// 1. 左为空// 2. 右为空// 3. 左右不为空if (cur->_left == nullptr){// 特判一下cur为根的情况,此时parent为空不能解引用// if (parent == nullptr)// 也可以用这个判断条件if (cur == _root){//左为空,指向右_root = _root->_right;}else{//链接时需要判断是根的左还是右,再将根的左或右链接cur的右if (cur == parent->_left){parent->_left = cur->_right;}else{parent->_right = cur->_right;}}//最后删除delete cur;}else if (cur->_right == nullptr){//右为空与左为空处理过程基本相同if (cur == _root){_root = _root->_left;}else{if (cur == parent->_left){parent->_left = cur->_left;}else{parent->_right = cur->_left;}}delete cur;}else{//左右不为空parent = cur;//当前要删除的节点//先找右子树的最小节点Node* minRight = cur->_right;while (minRight->_left){parent = minRight;minRight = minRight->_left;}//将minRight替换到curcur->_key = minRight->_key;//链接if (minRight == parent->_left){parent->_left = minRight->_right;}else{parent->_left = minRight->_right;}//删除delete minRight;}return true;}}return false;
}//递归版
bool EraseR(const K& key)
{return _EraseR(_root, key);
}
//root传引用,用于链接
bool _EraseR(Node*& root, const K& key)
{if (root == nullptr){return false;}if (key < root->_key){return _EraseR(root->_left, key);}else if (key > root->_key){return _EraseR(root->_right, key);}else{Node* del = root;if (root->_left == nullptr) //左为空{root = root->_right;}else if (root->_right == nullptr) //右为空{root = root->_left;}else //左右不为空,递归处理子树{Node* minRight = root->_right;while (minRight->_left){minRight = minRight->_left;}//替换swap(root->_key, minRight->_key);//递归处理子树:在右子树中删除keyreturn _EraseR(root->_right, key);}delete del;return true;}
}四、二叉搜索树的应用
- K模型:K模型即只有key作为关键码,结构中只需要存储Key即可,关键码即为需要搜索到的值。
比如:给一个单词word,判断该单词是否拼写正确,具体方式如下: 以词库中所有单词集合中的每个单词作为key,构建一棵二叉搜索树 在二叉搜索树中检索该单词是否存在,存在则拼写正确,不存在则拼写错误。
- KV模型:每一个关键码key,都有与之对应的值Value,即
<Key, Value>的键值对。
该种方式在现实生活中非常常见:
比如英汉词典就是英文与中文的对应关系,通过英文可以快速找到与其对应的中文,英文单词与其对应的中文<Word, Chinese>就构成一种键值对;
再比如统计单词次数,统计成功后,给定单词就可快速找到其出现的次数,单词与其出现次数就是<word, count>就构成一种键值对。
将二叉搜索树改造为KV结构也比较简单,整体代码:
二叉搜索树整体代码
五、二叉搜索树的性能分析
插入和删除操作都必须先查找,查找效率代表了二叉搜索树中各个操作的性能。
对有n个结点的二叉搜索树,若每个元素查找的概率相等,则二叉搜索树平均查找长度是结点在二 叉搜索树的深度的函数,即结点越深,则比较次数越多。
但对于同一个关键码集合,如果各关键码插入的次序不同,可能得到不同结构的二叉搜索树:
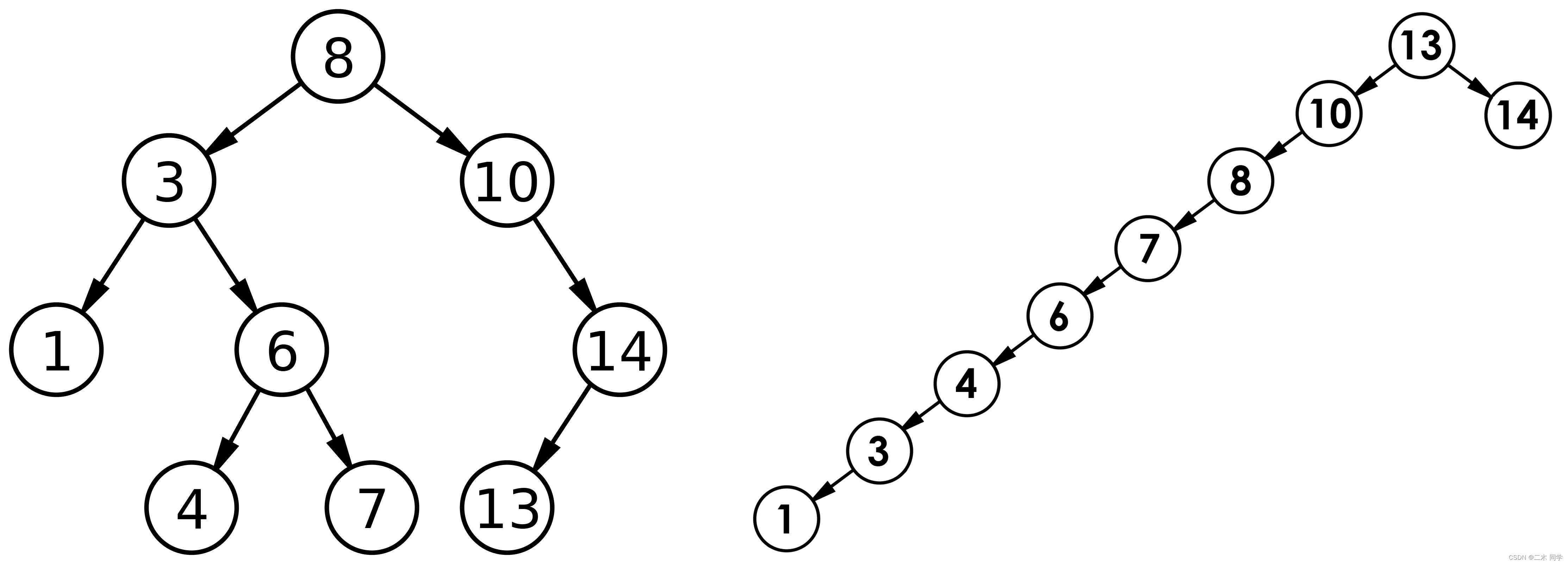
最优情况下,二叉搜索树为完全二叉树(或者接近完全二叉树),其平均比较次数为:log2Nlog_2 Nlog2N
最差情况下,二叉搜索树退化为单支树(或者类似单支),其平均比较次数为:N2\frac{N}{2}2N
问题:如果退化成单支树,二叉搜索树的性能就失去了。那能否进行改进,不论按照什么次序插入关键码,二叉搜索树的性能都能达到最优?此时AVL树和红黑树就可以上场了。
相关文章:

【C++】二叉搜索树的模拟实现
一、概念 二叉搜索树又称二叉排序树,它或者是一棵空树,或者是具有以下性质的二叉树: 若它的左子树不为空,则左子树上所有节点的值都小于根节点的值若它的右子树不为空,则右子树上所有节点的值都大于根节点的值它的左右子树也分别…...
HNU工训中心:元器件及测量基础实验报告
工训中心的牛马实验 1.实验目的 1.熟悉测量验证常用元器件参数、 并采用替代法(测量回路电流)测量其伏安特性的方法。 2.熟悉测量误差及减小测量误差注意事项 2.实验仪器和器材 1.实验仪器. 直流稳压电源型号:IT6302 台式多用表型号:UT805A 2.实验( 箱)器材 电路实验箱…...
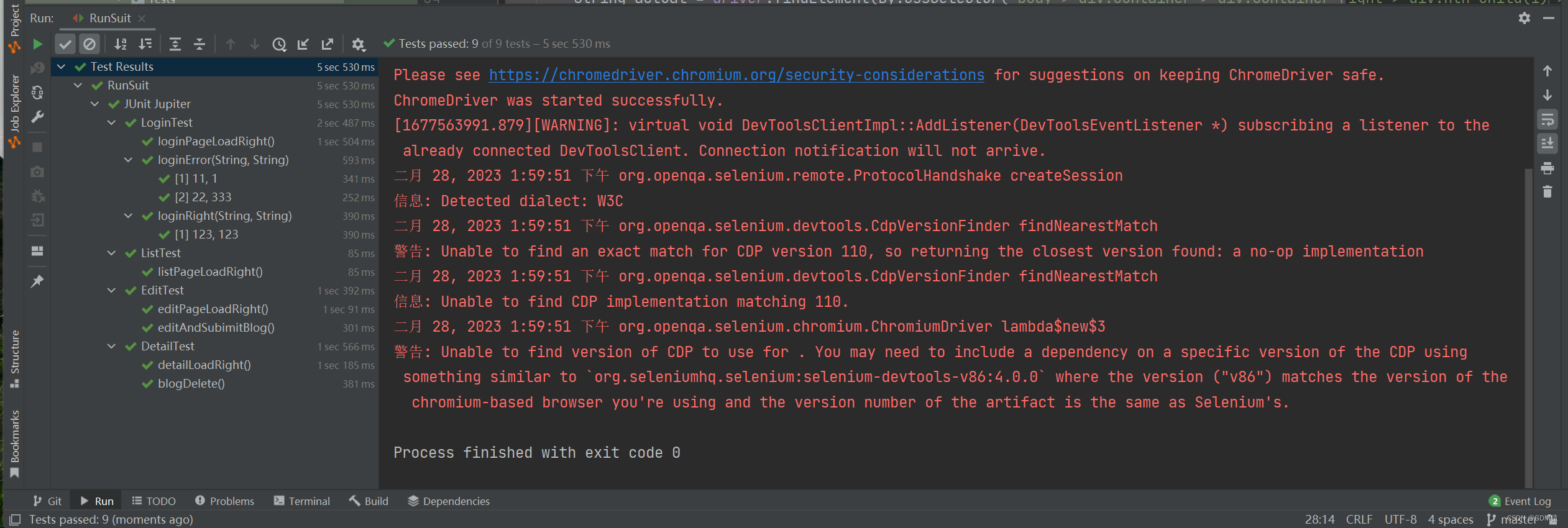
博客系统--自动化测试
项目体验地址(账号:123,密码:123)http://120.53.20.213:8080/blog_system/login.html项目后端说明:http://t.csdn.cn/32Nnv项目码云Gitee地址:https://gitee.com/GoodManSS/project/tree/master…...

Day903.自增主键不能保证连续递增 -MySQL实战
自增主键不能保证连续递增 Hi,我是阿昌,今天学习记录的是关于自增主键不能保证连续递增的内容。 MySql保证了主键是自增,但不相对连续;帮助开发人员快速识别每个行的唯一性,并提高查询效率。 自增主键可以让主键索引…...
02-MyBatis查询-
文章目录Mybatis CRUD练习1,配置文件实现CRUD1.1 环境准备Debug01: 别名mybatisx报错1.2 查询所有数据1.2.1 编写接口方法1.2.2 编写SQL语句1.2.3 编写测试方法1.2.4 起别名解决上述问题1.2.5 使用resultMap解决上述问题1.2.6 小结1.3 查询详情1.3.1 编写接口方法1.…...

外盘国际期货招商:2023年3月关注日历,把握重要投资机会
2023年3月大事件日历 关注大事日历,把握重要投资机会 3月1日:马斯克推出特斯拉宏图第三篇章 3月1-2日:G20外长会议 3月4-5日:全国两会召开 3月9日:中国2月CPI、PPI数据 待定(前次进行日期:…...
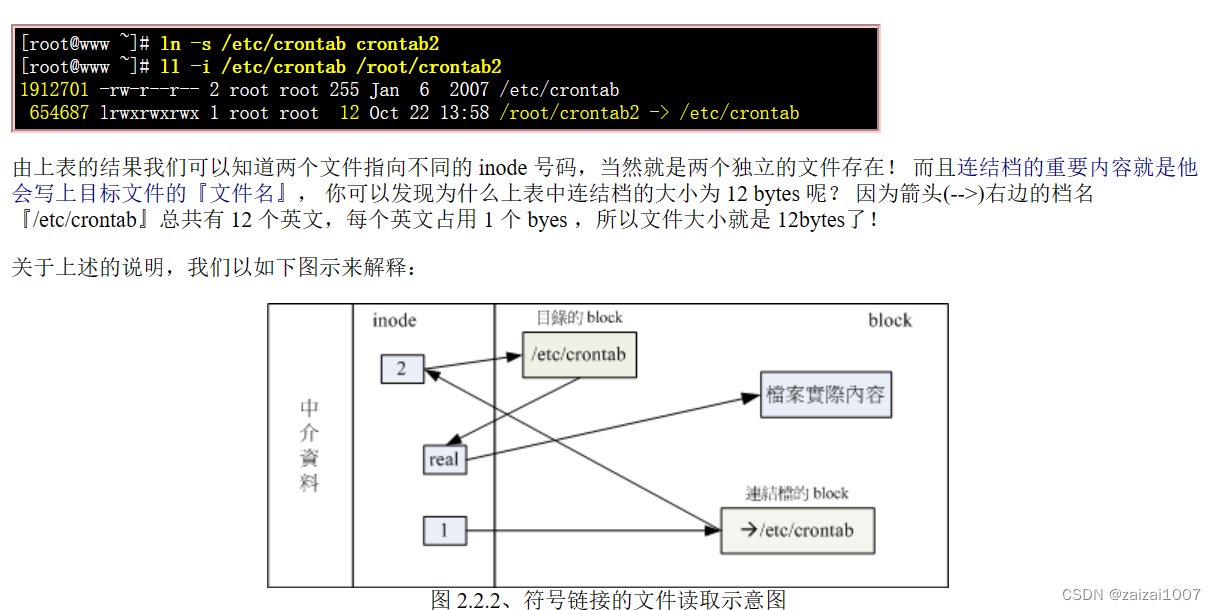
Linux学习(9.1)文件系统的简单操作
以下内容转载自鸟哥的Linux私房菜 原文:鸟哥的 Linux 私房菜 -- Linux 磁盘与文件系统管理 (vbird.org) 磁盘与目录的容量 df:列出文件系统的整体磁盘使用量;du:评估文件系统的磁盘使用量(常用在推估目录所占容量) df du 实体…...

Hadoop综合案例 - 聊天软件数据
目录1、聊天软件数据分析案例需求2、基于Hive数仓实现需求开发2.1 建库2.2 建表2.3 加载数据2.4 ETL数据清洗2.5 需求指标统计---都很简单3、FineBI实现可视化报表3.1 FineBI介绍3.2 FineBI配置数据3.3 构建可视化报表1、聊天软件数据分析案例需求 MR速度慢—引入hive 背景&a…...

Python进阶-----面向对象1.0(对象和类的介绍、定义)
目录 前言: 面向过程和面向对象 类和对象 Python中类的定义 (1)类的定义形式 (2)深层剖析类对象 前言: 感谢各位的一路陪伴,我学习Python也有一个月了,在这一个月里我收获满满…...

天猫淘宝企业服务为中小微企业打造供应链智能协同网络,让采购不再将就!丨爱分析报告
编者按:近日天猫淘宝企业服务&爱分析联合发布《2023中小微企业电商采购白皮书》,为中小微企业采购数字化带来红利。 某水泵企业:线上客户主要是中小微企业,线上业绩遇到瓶颈,如何突破呢?某焊割设备企业…...

基于四信网络摄像机的工业自动化应用
方案背景 随着数控机床被广泛的应用在工业生产中,数控技术发展成为制造业的核心。 鉴于数控机床的复杂性,以及企业人力储备有限,设备的监控和维护必须借助外部力量,而如何实现车间实时监测成了目前迫切解决的问题。 方案需求 ①兼…...

软件测试2
一 web掐断三大核心技术 HTML:负责网页的结构 CSS:负责网页的美化 JS:负责网页的行为 二 工具的使用 改变HBuilder文字的大小: 工具-视觉主题设置-大小22-确定 三 html简介 中文定义:超文本标记语言 新建一个html…...
leetcode162. 寻找峰值)
(二分查找)leetcode162. 寻找峰值
文章目录一、题目1、题目描述2、基础框架3、原题链接二、解题报告1、思路分析2、时间复杂度3、代码详解三、本题小知识一、题目 1、题目描述 峰值元素是指其值严格大于左右相邻值的元素。 给你一个整数数组 nums,找到峰值元素并返回其索引。数组可能包含多个峰值…...
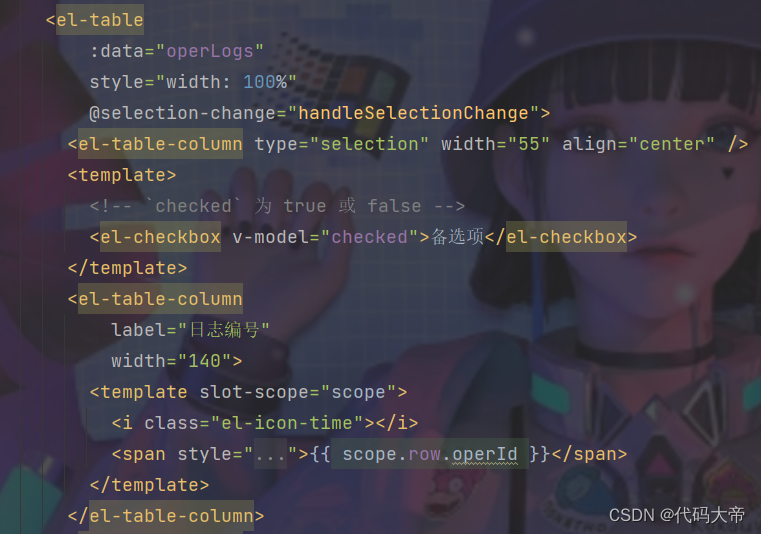
spring boot 配合element ui vue实现表格的批量删除(前后端详细教学,简单易懂,有手就行)
目录 一.前言: 二. 前端代码: 2.1.element ui组件代码 2.2删除按钮 2.3.data 2.4.methods 三.后端代码: 一.前言: 研究了其他人的博客,找到了一篇有含金量的,进行了部分改写实现前后端分离࿰…...
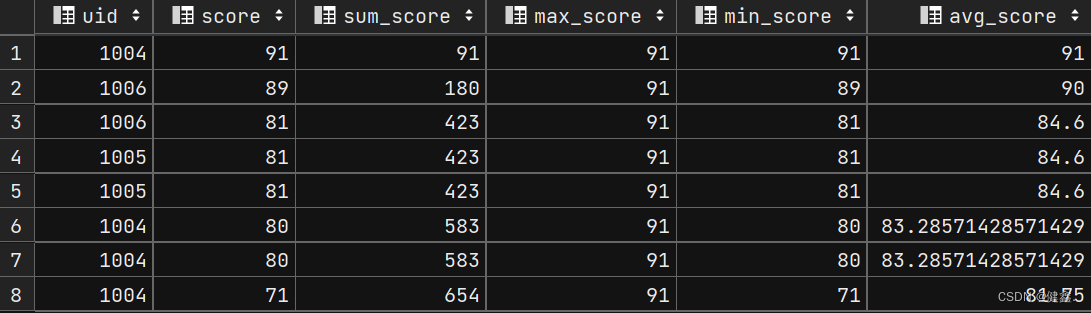
hiveSQL开窗函数详解
hive开窗函数 文章目录hive开窗函数1. 开窗函数概述1.1 窗口函数分类1.2 窗口函数和普通聚合函数的区别2. 窗口函数的基本用法2.1 基本用法2.2 设置窗口的方法2.2.1 window_name2.2.2 partition by2.2.3 order by 子句2.2.4 rows指定窗口大小窗口框架2.3 开窗函数中加 order by…...

深度学习基础实例与总结
一、神经网络 1 深度学习 1 什么是深度学习? 简单来说,深度学习就是一种包括多个隐含层 (越多即为越深)的多层感知机。它通过组合低层特征,形成更为抽象的高层表示,用以描述被识别对象的高级属性类别或特征。 能自生成数据的中…...

在 WIndows 下安装 Apache Tinkerpop (Gremlin)
一、安装 JDK 首先安装 Java JDK,这个去官网下载即可,我下载安装的 JDK19(jdk-19_windows-x64_bin.msi),细节不赘述。 二、去 Tinkerpop 网站下载 Gremlin 网址:https://tinkerpop.apache.org/ 点击下面…...

从软件的角度看待PCI和PCIE(一)
1.最容易访问的设备是什么? 是内存! 要读写内存,知道它的地址就可以了,不需要什么驱动程序; volatile unsigned int *p 0xffff8811; unsigned int val; *p val; val *p;只有内存能这样简单、方便的使用吗…...

DSP_TMS320F28377D_ADC学习笔记
前言 DSP各种模块的使用,基本上就是 GPIO复用配置、相关控制寄存器的配置、中断的配置。本文主要记录本人对ADC模块的学习笔记。TMS320F28377D上面有24路ADC专用IO,这意味着不需要进行GPIO复用配置。 只需要考虑相关控制寄存器和中断的配置。看代码请直…...
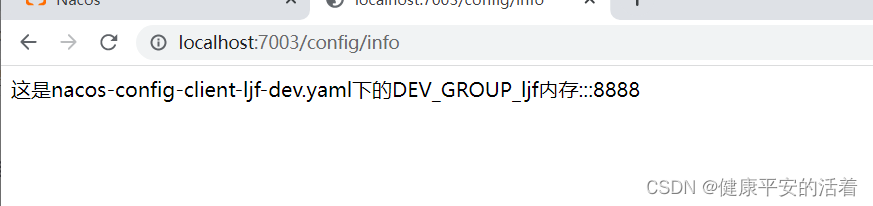
springcloud3 Nacos中namespace和group,dataId的联系
一 Namespance和group和dataId的联系 1.1 3者之间的联系 话不多说,上答案,如下图: namespance用于区分部署环境,group和dataId用于逻辑上区分两个目标对象。 二 案例:实现读取注册中心的不同环境下的配置文件 …...

RestClient
什么是RestClient RestClient 是 Elasticsearch 官方提供的 Java 低级 REST 客户端,它允许HTTP与Elasticsearch 集群通信,而无需处理 JSON 序列化/反序列化等底层细节。它是 Elasticsearch Java API 客户端的基础。 RestClient 主要特点 轻量级ÿ…...

conda相比python好处
Conda 作为 Python 的环境和包管理工具,相比原生 Python 生态(如 pip 虚拟环境)有许多独特优势,尤其在多项目管理、依赖处理和跨平台兼容性等方面表现更优。以下是 Conda 的核心好处: 一、一站式环境管理:…...

RocketMQ延迟消息机制
两种延迟消息 RocketMQ中提供了两种延迟消息机制 指定固定的延迟级别 通过在Message中设定一个MessageDelayLevel参数,对应18个预设的延迟级别指定时间点的延迟级别 通过在Message中设定一个DeliverTimeMS指定一个Long类型表示的具体时间点。到了时间点后…...

Leetcode 3576. Transform Array to All Equal Elements
Leetcode 3576. Transform Array to All Equal Elements 1. 解题思路2. 代码实现 题目链接:3576. Transform Array to All Equal Elements 1. 解题思路 这一题思路上就是分别考察一下是否能将其转化为全1或者全-1数组即可。 至于每一种情况是否可以达到…...

Qt/C++开发监控GB28181系统/取流协议/同时支持udp/tcp被动/tcp主动
一、前言说明 在2011版本的gb28181协议中,拉取视频流只要求udp方式,从2016开始要求新增支持tcp被动和tcp主动两种方式,udp理论上会丢包的,所以实际使用过程可能会出现画面花屏的情况,而tcp肯定不丢包,起码…...

【Oracle APEX开发小技巧12】
有如下需求: 有一个问题反馈页面,要实现在apex页面展示能直观看到反馈时间超过7天未处理的数据,方便管理员及时处理反馈。 我的方法:直接将逻辑写在SQL中,这样可以直接在页面展示 完整代码: SELECTSF.FE…...

可靠性+灵活性:电力载波技术在楼宇自控中的核心价值
可靠性灵活性:电力载波技术在楼宇自控中的核心价值 在智能楼宇的自动化控制中,电力载波技术(PLC)凭借其独特的优势,正成为构建高效、稳定、灵活系统的核心解决方案。它利用现有电力线路传输数据,无需额外布…...

YSYX学习记录(八)
C语言,练习0: 先创建一个文件夹,我用的是物理机: 安装build-essential 练习1: 我注释掉了 #include <stdio.h> 出现下面错误 在你的文本编辑器中打开ex1文件,随机修改或删除一部分,之后…...

蓝桥杯 2024 15届国赛 A组 儿童节快乐
P10576 [蓝桥杯 2024 国 A] 儿童节快乐 题目描述 五彩斑斓的气球在蓝天下悠然飘荡,轻快的音乐在耳边持续回荡,小朋友们手牵着手一同畅快欢笑。在这样一片安乐祥和的氛围下,六一来了。 今天是六一儿童节,小蓝老师为了让大家在节…...

【论文笔记】若干矿井粉尘检测算法概述
总的来说,传统机器学习、传统机器学习与深度学习的结合、LSTM等算法所需要的数据集来源于矿井传感器测量的粉尘浓度,通过建立回归模型来预测未来矿井的粉尘浓度。传统机器学习算法性能易受数据中极端值的影响。YOLO等计算机视觉算法所需要的数据集来源于…...
