数据结构-归并排序+计数排序
1.归并排序
基本思想:
归并排序是建立在归并操作上的一种有效的排序算法,该算法是采用分治法的一个非常典型的应用。将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。若将两个有序表合并成一个有序表,称为二路归并。 归并排序核心步骤:
相当于每次把待排数据分为两个子区间,如果每个子区间有序,再让两个子区间归并起来也有序,那整体就有序了。我们可以按照二叉树的思想,把子区间再分为两份,使子区间的子区间有序.......直到子区间分无可分为止。
具体过程如下:
那该如何让两个有序子区间归并呢?
直接在数组中肯定不行,这样会发生数据的覆盖。所以我们可以像之前合并两个有序数组一样,另外开辟一个空间tmp,依次比较两个有序子区间的值,每次比较后把较小的放在tmp中,如果其中一个子区间提前结束,就把另外一个子区间的剩余的数据全放进tmp,最后把tmp中的数据拷贝回原数组。
使用递归实现:
#include<stdio.h> #include<stdlib.h> void _MegeSort(int* a, int begin, int end,int*tmp) {//只剩一个数据,递归结束if (begin == end){return;}int mid = (begin + end) / 2;//递归子区间,分为两部分_MegeSort(a, begin, mid, tmp);_MegeSort(a, mid+1, end, tmp);int begin1 = begin, end1 = mid;int begin2 = mid + 1, end2 = end;int j = begin;//两部分比较,每次小的放入tmpwhile (begin1 <= end1 && begin2 <= end2){if (a[begin1] < a[begin2]){tmp[j++] = a[begin1++];}else{tmp[j++] = a[begin2++];}}//哪部分有剩余,全部放入tmpwhile (begin1 <= end1){tmp[j++] = a[begin1++];}while (begin2 <= end2){tmp[j++] = a[begin2++];}//拷贝到原数组memcpy(a + begin, tmp + begin, sizeof(int) * (end - begin + 1)); } void MegeSort(int* a, int n) {int* tmp = (int*)malloc(sizeof(int) * n);_MegeSort(a, 0, n - 1, tmp);free(tmp); }void Print(int* a, int n) {for (int i = 0; i < n; i++){printf("%d ",a[i]);}printf("\n"); } int main() {int a[] = { 1,4,9,6,3,5,2,8,10,7,11,1};MegeSort(a, sizeof(a) / sizeof(int));Print(a, sizeof(a) / sizeof(int));return 0; }注意:
1. 因为每次递归的子区间都不一定是从0开始的,所以我们拷贝数据时,最好从begin的位置开始:
//拷贝到原数组 memcpy(a + begin, tmp + begin, sizeof(int) * (end - begin + 1));2. 在代码中j作为tmp的坐标,每次往tmp中放入数据后都要加一,但不能初始化为0,否则每次递归进入,j的值都会清0,所以最好初始化:j=begin
归并排序的复杂度:
时间复杂度:O(N*logN)
归并排序每次递归都要把待排数据分为两份,相当于二分法,那一共有logN层递归,而每次递归都要比较数据,要把每个数据都遍历一遍,每层的时间复杂度就是O(N),所以总共的时间复杂度是O(N*logN)。
空间复杂度:O(N)
刚开始就开辟了空间,此时就已经是O(N)了,而递归过程中函数栈帧的创建是logN,所以总的空间复杂度是:O(N+logN),但是量级没变,还是O(N)。
2.非递归实现归并排序
非递归实现归并排序,我们只需模拟上述的递归过程即可,把递归过程转换为:把数据先分为2个一组,全部归并一遍,拷贝回原数组,然后4个一组,全部归并一遍,拷贝回原数组,再8个一组, 全部归并一遍,拷贝回原数组,
那我们就可以设置一个gap,两个数据为一组时,gap=1,每归并一组数据就往后跳2*gap步,直到全部归并一遍,再次分组,这次gap=2,每归并一组数据往后跳2*gap步,直到全部归并一遍,下次gap=4,跳2*gap步.....,直到gap>n就停止,
代码如下:
void MegeSortNonR(int* a, int n) {int* tmp = (int*)malloc(sizeof(int) * n);if (tmp == NULL){perror("malloc fail\n");return;}int gap = 1;while (gap < n){int j = 0;for (int i = 0; i < n; i += 2 * gap){int begin1 = i, end1 = i + gap - 1;int begin2 = i + gap, end2 = i + 2 * gap - 1;//两部分比较,每次小的放入tmpwhile (begin1 <= end1 && begin2 <= end2){if (a[begin1] < a[begin2]){tmp[j++] = a[begin1++];}else{tmp[j++] = a[begin2++];}}//哪部分有剩余,全部放入tmpwhile (begin1 <= end1){tmp[j++] = a[begin1++];}while (begin2 <= end2){tmp[j++] = a[begin2++];}}memcpy(a, tmp, sizeof(int) * n);gap *= 2;}free(tmp); }测试一下:
上面结果看起来,我们排序成功了,但是上述代码真的对吗?
上面代码我们在测试时用的是8个数据,但是如果用9个、10个等,就会发现排序并不会成功,可能程序还会崩掉,这是为什么呢?
因为我们在分组时,是按照固定的2的次方分的,一旦数据个数不是2、4、8的次方,后面归并时就会发生越界问题。
下面我们给10个数据打印一下边界,会发现,有三种越界的方式,:
那我们对这三种情况分别做一下处理:
第1、2种情况出现时,我们直接break,第三种情况,我们修改边界,令end2=n-1,但是注意直接break后,第1、2种情况往tmp中归并时会少一部分数据(如上图蓝框所示),所以最后把tmp的数据往a中拷贝时,不能一次性全部拷贝回去,否则a中这些数据就永远丢失了,所以最好归并一段,拷贝一段,这样拷贝过去的数据只会把前面的数据覆盖,没参与归并的数据还在a中。
代码如下:
void MegeSortNonR(int* a, int n) {int* tmp = (int*)malloc(sizeof(int) * n);if (tmp == NULL){perror("malloc fail\n");return;}int gap = 1;while (gap < n){int j = 0;for (int i = 0; i < n; i += 2 * gap){int begin1 = i, end1 = i + gap - 1;int begin2 = i + gap, end2 = i + 2 * gap - 1;if (end1 >= n || begin2 >= n){break;}//修正if (end2 >= n){end2 = n - 1;}//两部分比较,每次小的放入tmpwhile (begin1 <= end1 && begin2 <= end2){if (a[begin1] < a[begin2]){tmp[j++] = a[begin1++];}else{tmp[j++] = a[begin2++];}}//哪部分有剩余,全部放入tmpwhile (begin1 <= end1){tmp[j++] = a[begin1++];}while (begin2 <= end2){tmp[j++] = a[begin2++];}//归并一段,拷贝一段memcpy(a+i, tmp+i, sizeof(int) * (end2-i+1));}gap *= 2;}free(tmp); }
3.计数排序
基本思想:
1. 统计每个数据出现的次数。
2. 根据数据的次数排序。
如果我们要排序的数在0~9之间,我们可以像上面一样开辟10个int大小的空间,统计待排数据中每个数据的个数,在开辟出的数组的相应下标处计数,那如果我们要排序的数据在100~109之间呢?难道开辟110个空间吗?
当然不是,我们可以做相对映射,在开辟空间之前,先找到待排数据中的最小值和最大值,开辟空间的大小就是:sizeof(int)*(max-min+1),开辟出的数组下标应该是:0~9,0~9下标的位置分别对应的是100~109,计数时,在下标为该数据减待排数据中的最小值的位置统计次数,例如:109就在109-100=9的下标处统计次数,统计完排序的时候再加上最小值即可。
代码如下:
#include<stdio.h> #include<stdlib.h> void CountSort(int* a, int n) {int min = a[0], max = a[0];//找最大值和最小值for (int i = 0; i < n; i++){if (a[i] < a[0]){min = a[i];}if (a[i] > a[0]){max = a[i];}}int range = max - min + 1;int* count = (int*)malloc(sizeof(int) * range);memset(count, 0, sizeof(int) * range);//计数for (int i = 0; i < n; i++){count[a[i] - min]++;}//排序int k = 0;for (int j = 0; j < range; j++){while (count[j]--){a[k++] = j + min;}} } //打印函数 Print(int* a, int n) {for (int i = 0; i < n; i++){printf("%d ", a[i]);}printf("\n"); } int main() {int a[] = { 6,1,6,7,9,6,4,5,6,1 };CountSort(a, sizeof(a) / sizeof(int));Print(a, sizeof(a) / sizeof(int));return 0; }
计数排序的复杂度:
时间复杂度:O(N+range)
寻找最大值和最小值时,遍历一遍数组,时间复杂度是:O(N),由于待排数据的范围是range,排序时所耗费的时间复杂度是:O(range),所以最终的时间复杂度是:O(N+range)
如果知道N和range的大小,N大,就是O(N),range大,就是O(range)。
空间复杂度:O(range)
额外开辟的空间个数是range,所以空间复杂度就是:O(range)
4.排序的复杂度和稳定性
总结如下:

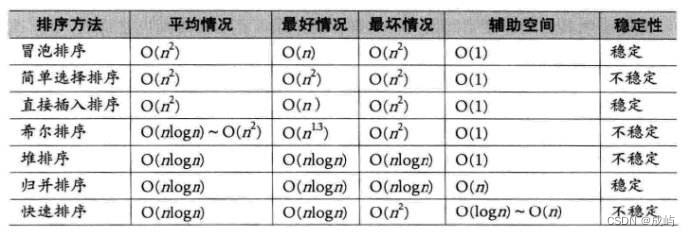
以上就是排序学习的全部内容了,到这,数据结构的学习就告一段落了,近期会停更一段时间,用来复习,后面将继续学习C++的知识,
未完待续。。。
相关文章:

数据结构-归并排序+计数排序
1.归并排序 基本思想: 归并排序是建立在归并操作上的一种有效的排序算法,该算法是采用分治法的一个非常典型的应用。将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。若将两个有序表合并成一个…...
Qml使用cpp文件的信号槽
文章目录 一、C文件Demo二、使用步骤1. 初始化C文件和QML文件,并建立信号槽2.在qml中调用 一、C文件Demo Q_INVOKABLE是一个Qt元对象系统中的宏,用于将C函数暴露给QML引擎。具体来说,它使得在QML代码中可以直接调用C类中被标记为Q_INVOKABLE的…...
聚类笔记:HDBSCAN
1 算法介绍 DBSCAN/OPTICS层次聚类主要由以下几步组成 空间变换构建最小生成树构建聚类层次结构(聚类树)压缩聚类树提取簇 2 空间变换 用互达距离来表示两个样本点之间的距离 ——>密集区域的样本距离不受影响——>稀疏区域的样本点与其他样本点的距离被放大——>…...

【Python】批量将PDG合成PDF,以及根据SS号重命名秒传的文件
目录 说明批量zip2pdf批量zip2pdf下载SS号重命名源代码SS号重命名源代码下载附录,水文年鉴 说明 1、zip2pdf是一个开源软件,支持自动化解压压缩包成PDG,PDG合成PDF,笔者在其基础上做了部分修改,支持批量转换。 2、秒…...
2023亚太杯数学建模A题思路 - 采果机器人的图像识别技术
# 1 赛题 问题A 采果机器人的图像识别技术 中国是世界上最大的苹果生产国,年产量约为3500万吨。与此同时,中国也是世 界上最大的苹果出口国,全球每两个苹果中就有一个,全球超过六分之一的苹果出口 自中国。中国提出了一带一路倡议…...

3、LeetCode之无重复字符的最长子串
给定一个字符串 s ,请你找出其中不含有重复字符的 最长子串 的长度 输入: s "abcabcbb" 输出: 3 解释: 因为无重复字符的最长子串是 "abc",所以其长度为 3。转载: C常用语法——unordered_set 题目主要思想ÿ…...

CONDITIONS EVALUATION REPORT-解决方案
在启动SpringBoot项目时,提示一堆的Positive matches、Negative matches(如下代码框),感觉像是报错了样。但用SpringBoot的Test类操作数据库的Insert是成功的。提示这些信息通过网上搜索主要讲配置类被Spring容器加载与被加载的说明。名词解释…...
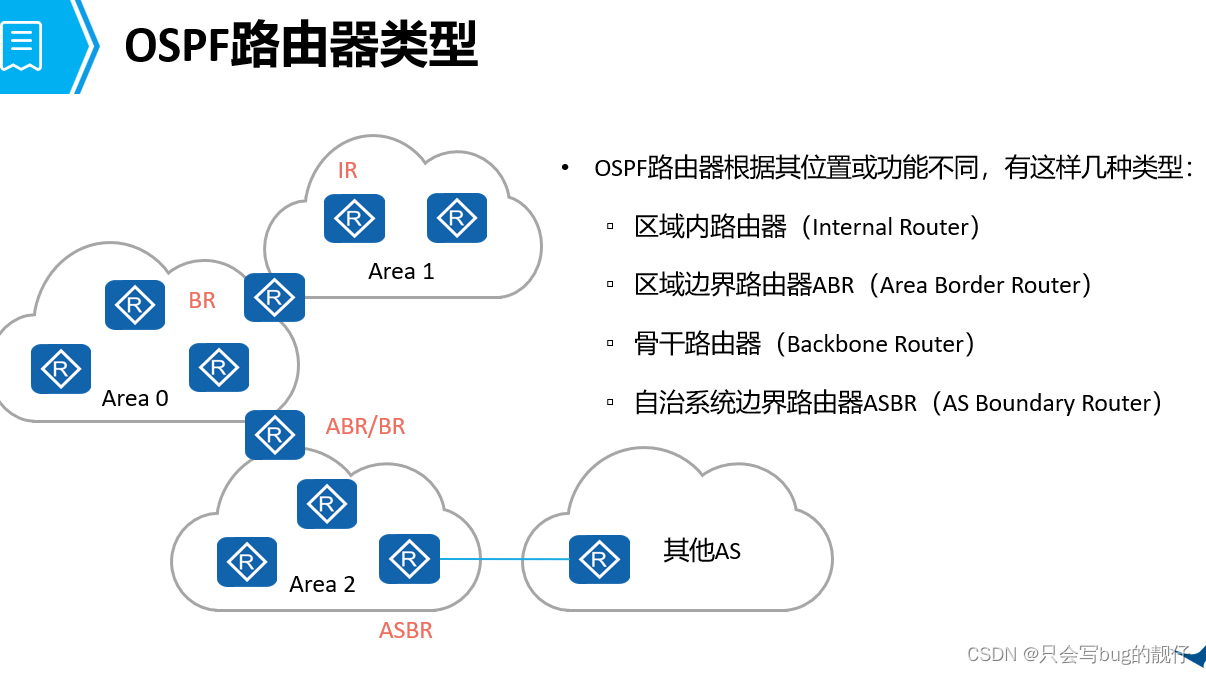
计算机网络——路由
文章目录 1. 前言:2. 路由基础2.1. 路由的相关概念2.2. 路由的特征2.3. 路由的过程 3 路由协议3.1. 静态路由:3.2. 动态路由:3.2.1. 距离矢量协议3.2.2. OSPF协议:3.2.2.1.OSPF概述OSPF的工作原理路由计算功能特性 3.2.2.2.OSPF报…...

python+requests+pytest+allure自动化框架
1.核心库 requests request请求 openpyxl excel文件操作 loggin 日志 smtplib 发送邮件 configparser unittest.mock mock服务 2.目录结构 base utils testDatas conf testCases testReport logs 其他 2.1base base_path.py 存放绝对路径,dos命令或Jenkins执行…...

css3
基础 <!DOCTYPE html> <html><head><meta charset"utf-8"><title>style</title><!-- link(外部样式)和style(内部样式)优先级相同,重复写会覆盖 --><link re…...

超级应用平台(HAP)起航
各位明道云用户和伙伴, 今天,我们正式发布明道云10.0版本。从这个版本开始,我们将产品名称正式命名为超级应用平台(Hyper Application Platform, 简称HAP)。我们用“超级”二字表达产品在综合能力方面的突破ÿ…...

cocos2dx Animate3D(二)
Twirl 扭曲旋转特效 // 持续时间(时间过后不会回到原来的样子) // 整个屏幕被分成几行几列 // 扭曲中心位置 // 扭曲的数量 // 振幅 static Twirl* create(float duration, const Size& gridSize, const Vec2& position, unsigned int twirls, float amplitude)…...
基于java技术的社区交易二手平台
基于java技术的社区交易二手平台的设计与实现 (一)开发背景 随着因特网的日益普及与发展,更多的人们开始通过因特网来寻求便利。但是,许多人都觉得网上商店里的东西不贵。所以,有些顾客宁愿去那些用二次定价建立起来的…...
(Matalb回归预测)GA-BP遗传算法优化BP神经网络的多维回归预测
目录 一、程序及算法内容介绍: 基本内容: 亮点与优势: 二、实际运行效果: 三、部分代码: 四、分享本文全部代码数据说明手册: 一、程序及算法内容介绍: 基本内容: 本代码基于M…...

【Docker】从零开始:10.registry搭建私有仓库
【Docker】从零开始:10.registry搭建私有仓库 为什么要使用私有仓库关于Docker Registry基于容器搭建registry私有仓库1.下载镜像2. 启动镜像3.修改系统配置文件4.下载ubuntu镜像,修改名称3.提交镜像4.查看镜像 本地搭建私有仓库(目前编译报错找不到包&a…...
树莓派上使用Nginx通过内网穿透实现无公网IP访问内网本地站点
前言 安装 Nginx(发音为“engine-x”)可以将您的树莓派变成一个强大的 Web 服务器,可以用于托管网站或 Web 应用程序。相比其他 Web 服务器,Nginx 的内存占用率非常低,可以在树莓派等资源受限的设备上运行。同时结合c…...

长征故事vr互动教育体验系统让师生感同身受
红色文化是贯穿于新民主主义革命、社会主义建设的各个时期,具有深厚的历史价值和文化内涵的先进文化,是高效、优质的教育资源。思政课vr红色数字展馆充分开发和大力弘扬红色文化资源,发挥其独特资源优势和教育功能,应用到教学中&a…...
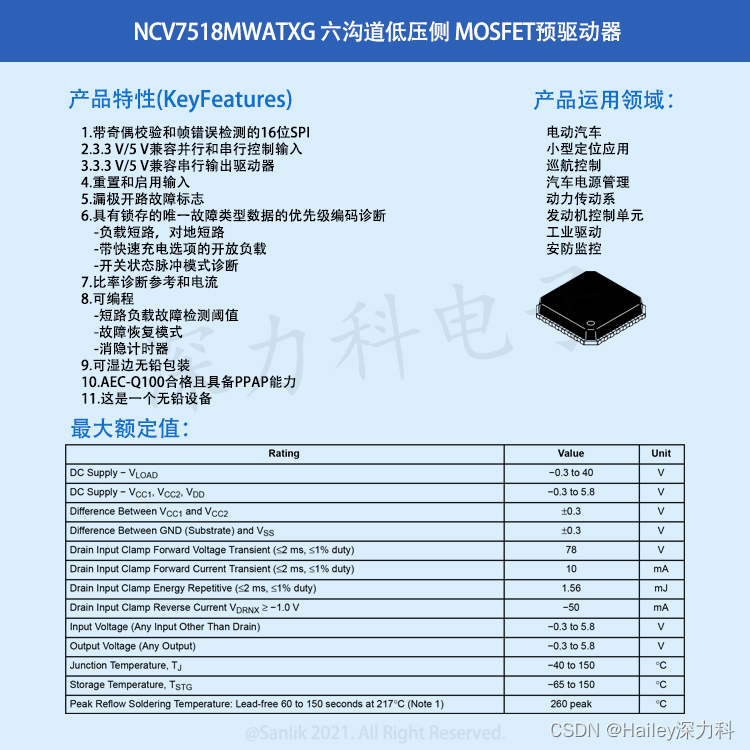
汽车级芯片NCV7518MWATXG 可编程六沟道低压侧 MOSFET预驱动器 特点、参数及应用
NCV7518MWATXG 可编程六沟道低压侧 MOSFET 预驱动器属于 FLEXMOS™ 汽车级产品,用于驱动逻辑电平 MOSFET。该产品可通过串行 SPI 和并行输入组合控制。该器件提供 3.3 V/5 V 兼容输入,并且串行输出驱动器可以采用 3.3 V 或 5 V 供电。内部通电重置提供受…...

【分布式】小白看Ring算法 - 03
相关系列 【分布式】NCCL部署与测试 - 01 【分布式】入门级NCCL多机并行实践 - 02 【分布式】小白看Ring算法 - 03 【分布式】大模型分布式训练入门与实践 - 04 概述 NCCL(NVIDIA Collective Communications Library)是由NVIDIA开发的一种用于多GPU间…...

使用Git bash切换Gitee、GitHub多个Git账号
Git是分布式代码管理工具,使用命令行的方式提交commit、revert回滚代码。这里介绍使用Git bash软件来切换Gitee、GitHub账号。 假设在gitee.com上的邮箱是alicefoxmail.com 、用户名为alice;在github上的邮箱是bobfoxmail.com、用户名为bob。 账号…...

学校招生小程序源码介绍
基于ThinkPHPFastAdminUniApp开发的学校招生小程序源码,专为学校招生场景量身打造,功能实用且操作便捷。 从技术架构来看,ThinkPHP提供稳定可靠的后台服务,FastAdmin加速开发流程,UniApp则保障小程序在多端有良好的兼…...

dify打造数据可视化图表
一、概述 在日常工作和学习中,我们经常需要和数据打交道。无论是分析报告、项目展示,还是简单的数据洞察,一个清晰直观的图表,往往能胜过千言万语。 一款能让数据可视化变得超级简单的 MCP Server,由蚂蚁集团 AntV 团队…...

rnn判断string中第一次出现a的下标
# coding:utf8 import torch import torch.nn as nn import numpy as np import random import json""" 基于pytorch的网络编写 实现一个RNN网络完成多分类任务 判断字符 a 第一次出现在字符串中的位置 """class TorchModel(nn.Module):def __in…...

2025年渗透测试面试题总结-腾讯[实习]科恩实验室-安全工程师(题目+回答)
安全领域各种资源,学习文档,以及工具分享、前沿信息分享、POC、EXP分享。不定期分享各种好玩的项目及好用的工具,欢迎关注。 目录 腾讯[实习]科恩实验室-安全工程师 一、网络与协议 1. TCP三次握手 2. SYN扫描原理 3. HTTPS证书机制 二…...

基于Springboot+Vue的办公管理系统
角色: 管理员、员工 技术: 后端: SpringBoot, Vue2, MySQL, Mybatis-Plus 前端: Vue2, Element-UI, Axios, Echarts, Vue-Router 核心功能: 该办公管理系统是一个综合性的企业内部管理平台,旨在提升企业运营效率和员工管理水…...

用鸿蒙HarmonyOS5实现中国象棋小游戏的过程
下面是一个基于鸿蒙OS (HarmonyOS) 的中国象棋小游戏的实现代码。这个实现使用Java语言和鸿蒙的Ability框架。 1. 项目结构 /src/main/java/com/example/chinesechess/├── MainAbilitySlice.java // 主界面逻辑├── ChessView.java // 游戏视图和逻辑├──…...

【Veristand】Veristand环境安装教程-Linux RT / Windows
首先声明,此教程是针对Simulink编译模型并导入Veristand中编写的,同时需要注意的是老用户编译可能用的是Veristand Model Framework,那个是历史版本,且NI不会再维护,新版本编译支持为VeriStand Model Generation Suppo…...

CTF show 数学不及格
拿到题目先查一下壳,看一下信息 发现是一个ELF文件,64位的 用IDA Pro 64 打开这个文件 然后点击F5进行伪代码转换 可以看到有五个if判断,第一个argc ! 5这个判断并没有起太大作用,主要是下面四个if判断 根据题目…...

【阅读笔记】MemOS: 大语言模型内存增强生成操作系统
核心速览 研究背景 研究问题:这篇文章要解决的问题是当前大型语言模型(LLMs)在处理内存方面的局限性。LLMs虽然在语言感知和生成方面表现出色,但缺乏统一的、结构化的内存架构。现有的方法如检索增强生成(RA…...

自定义线程池1.2
自定义线程池 1.2 1. 简介 上次我们实现了 1.1 版本,将线程池中的线程数量交给使用者决定,并且将线程的创建延迟到任务提交的时候,在本文中我们将对这个版本进行如下的优化: 在新建线程时交给线程一个任务。让线程在某种情况下…...







