Crypto(11)HECTF-rsarsa(明文存在线性关系)
题目如下:
from functools import reduce
from Crypto.Util.number import *
import random
from secret import flag,hintdef generate_PQ(bits):x = getPrime(bits) >> bits//2 << bits//2#右移bit//2位后左移bit//2位while True:p = x + random.getrandbits(bits//2)#x是前一步生成的大素数,加上一个bit//2的随机数if isPrime(p):#判断是否位素数breakwhile True:q = x + random.getrandbits(bits//2)if isPrime(q):breakreturn p,qm = bytes_to_long(flag)
hint = bytes_to_long(hint)
e = 65537
p,q = generate_PQ(1024)#用generate_PQ函数生成两个大素数p,q,1024是参数
n = p*q
random.seed(seed)
x = [random.randint(1,seed) for _ in range(2)]#包含两个元素的列表,每个元素都是在指定范围内生成的伪随机整数
y = [random.randint(1,seed) for _ in range(2)]print("c =",pow(hint,e,n))
print("n =",n)
print("c1 =",pow(reduce(lambda x, y: x * m + y, x), 17, n))#对x列表中的元素
print("c2 =",pow(reduce(lambda x, y: x * m + y, y), 17, n))#对y列表中的元素对题目进行审计
p、q的生成逻辑如下:
def generate_PQ(bits):x = getPrime(bits) >> bits//2 << bits//2while True:p = x + random.getrandbits(bits//2)if isPrime(p):breakwhile True:q = x + random.getrandbits(bits//2)if isPrime(q):breakreturn p,qp、q的前512位是一样的,只有后512位不同,且是 random.getrandbits()生成的。影响不大 比较接近(即认为p=q)
自己本地多试试这个生成过程之后,可以得出: p+q = 2*(gmpy2.iroot(p*q,n)[0] + 1)(gmpy2.root(q,n)用于求q的n次方根,向下取整,故+1)
因此 phi_n = n - (p+q) + 1 进而求d 正常解rsa即可(注:phi_n=(p-1)^2 , p=q)
exp如下:
from Crypto.Util.number import *import gmpy2c = 23001012057110779471190091625946693776382380529397302126337301229214301450335125076016991835054198112255974220434689958104931664098817350134656616154892781885504255726632558690544057380195511404078662094726952602350250840712610362029824982069179543810686494204685887486972937880502875441232004432323308734978847464589775857815430854038396134952486665687531579988133729365443247597395131516449487146786214227230853061720614077115599878358089377114269765796099004940883513036567103436154122335792598432012140232905658895014924069330265282364249236142072335363164451294973492092043110680377767954710822286121195290921259n = 25797576442752368834409243494498462987370374608513814739930733437032797864549696772439769896270235017474841764016848627149724764584643408544417890463920153063835758878658712790547466715525246861709503145754424896044647787146006099053059124466248594151765065039034244830614724509092882854620642569723528913880146979990993657935598837645247839225413889995373643109990149255485373119338024345925311643249141660177285328457994476509430988280481564046398593906405870633323621548853838399385539924067139236445142933316057900841508972844270649504321178274091144241788883353514769368447833090379142367062327674855735832181241c1 = 5702553209026762891130621254037294747819864952568824327221430749829654552175171307151888953348659971422228556686092434932000213695492351602755144510029319044193567051613888876933660356756790444392278614143455408803808095980542751023095024106689759843322130186219560734082292015929006937318400901378373771587448471762923415750064340829545587346927358411518874090282598069394946985795177419501659425500481799157093068337225389827654860680897913114945871197415129055139716514884716404289565297854681809258375973195355836553939670482515484347869258398517276876478311544109924573128946617113822561968330536525876279165313c2 = 17562619948191690401152271053920025392401205523418067246455197241332062181407775133406742024747779181762812656501246379566147855594504112107873162350649668441267907193889705868572309785100582281795380779594946422800722070311908572538672508371123334385630310655242811756206073131919770939609347021343765434127086363844595938894714892990053114153402729297796655717510572619694559203260762574159375142757462082162882775921182437134358375300674547217425590072112733480640372328934982979603312597484512120618223179217692002851194538130349201457319160001114007059615596355221194709809437500052122684989302563103918409825040e = 65537x = gmpy2.iroot(n,2)[0]p_and_q = x*2 + 2phi_n = n - p_and_q + 1d = gmpy2.invert(e,phi_n)hint = pow(c,d,n)print("Hint:",long_to_bytes(hint))得到:Hint: b'Hint{Seed_is_256087_+_396445_-_538018}'
因此可以计算出 seed值为:114514
所以
-
x=[30509,13601] -
y=[92095,27065]
可以得到:
-
c1 = (30509*m + 13601)^17 mod n -
c2 = (92095*m + 27065)^17 mod n
明文存在线性关系类型题目,可以按rsa再次解密一下
也可以利用 ** Related Message Attack**
sagemath exp如下:
#Related Message Attack 解题脚本# 条件:已知 e、n c1 = (a*m+b)^e mod n c2 = (c*m+d)^e mod n# 即相同的公钥[e, n]去加密线性变换后的m#Sageimport binasciidef attack(c1, c2, n, e):PR.<x>=PolynomialRing(Zmod(n))# replace a,b,c,dg1 = (30509*x+13601)^e - c1g2 = (92095*x+27065)^e - c2def gcd(g1, g2):while g2:g1, g2 = g2, g1 % g2return g1.monic()return -gcd(g1, g2)[0]n = 25797576442752368834409243494498462987370374608513814739930733437032797864549696772439769896270235017474841764016848627149724764584643408544417890463920153063835758878658712790547466715525246861709503145754424896044647787146006099053059124466248594151765065039034244830614724509092882854620642569723528913880146979990993657935598837645247839225413889995373643109990149255485373119338024345925311643249141660177285328457994476509430988280481564046398593906405870633323621548853838399385539924067139236445142933316057900841508972844270649504321178274091144241788883353514769368447833090379142367062327674855735832181241c1 = 5702553209026762891130621254037294747819864952568824327221430749829654552175171307151888953348659971422228556686092434932000213695492351602755144510029319044193567051613888876933660356756790444392278614143455408803808095980542751023095024106689759843322130186219560734082292015929006937318400901378373771587448471762923415750064340829545587346927358411518874090282598069394946985795177419501659425500481799157093068337225389827654860680897913114945871197415129055139716514884716404289565297854681809258375973195355836553939670482515484347869258398517276876478311544109924573128946617113822561968330536525876279165313c2 = 17562619948191690401152271053920025392401205523418067246455197241332062181407775133406742024747779181762812656501246379566147855594504112107873162350649668441267907193889705868572309785100582281795380779594946422800722070311908572538672508371123334385630310655242811756206073131919770939609347021343765434127086363844595938894714892990053114153402729297796655717510572619694559203260762574159375142757462082162882775921182437134358375300674547217425590072112733480640372328934982979603312597484512120618223179217692002851194538130349201457319160001114007059615596355221194709809437500052122684989302563103918409825040e = 17m1 = attack(c1, c2, n, e)print(binascii.unhexlify("%x" % int(m1)))得到flag:b'HECTF{r3411y_easy_R4nd0m_And_r3l4ted_m3554ge_att4ck}'
相关文章:
HECTF-rsarsa(明文存在线性关系))
Crypto(11)HECTF-rsarsa(明文存在线性关系)
题目如下: from functools import reduce from Crypto.Util.number import * import random from secret import flag,hintdef generate_PQ(bits):x getPrime(bits) >> bits//2 << bits//2#右移bit//2位后左移bit//2位while True:p x random.getran…...
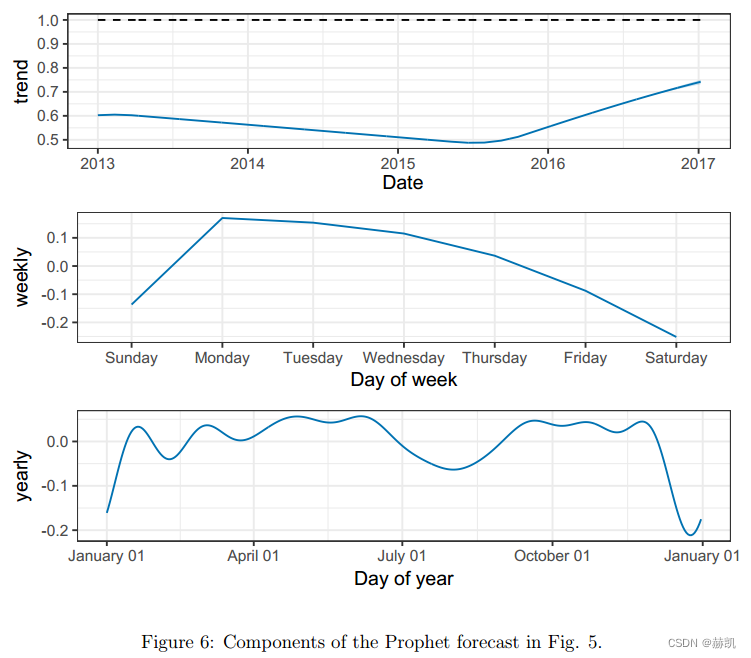
论文阅读 Forecasting at Scale (二)
最近在看时间序列的文章,回顾下经典 论文地址 项目地址 Forecasting at Scale 3.2、季节性 3.3、假日和活动事件3.4、模型拟合3.5、分析师参与的循环建模4、自动化预测评估4.1、使用基线预测4.2、建模预测准确性4.3、模拟历史预测4.4、识别大的预测误差 5、结论6、致…...

刷题感悟w
题目很长的一定要慢慢把题目的意思搞清楚 有重复操作不知道怎么办 可以用数组去标记 你好!在C中,replace 函数通常是用于替换容器(例如 std::vector 或 std::string)中的特定元素的函数。以下是 std::replace 函数的一般用法&…...
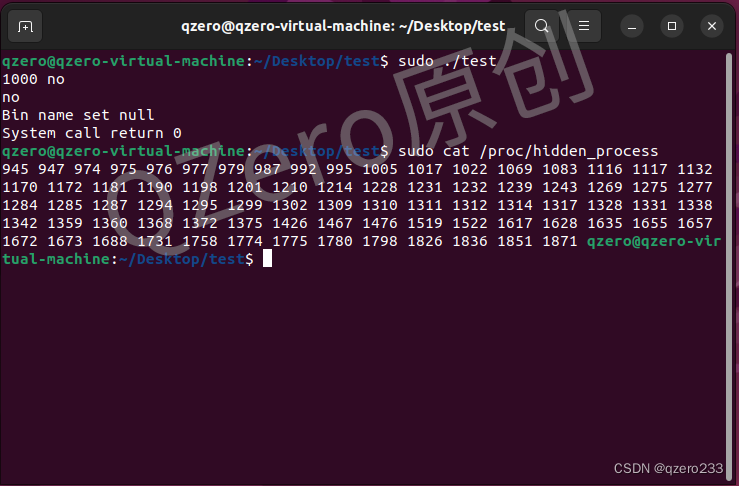
记一次linux操作系统实验
前言 最近完成了一个需要修改和编译linux内核源码的操作系统实验,个人感觉这个实验还是比较有意思的。这次实验总共耗时4天,从对linux实现零基础,通过查阅资料和不断尝试,直到完成实验目标,在这过程中确实也收获颇丰&…...

java操作富文本插入到word模板
最近项目有个需求,大致流程是前端保存富文本(html的代码)到数据库,后台需要将富文本代码转成带格式的文字,插入到word模板里,然后将word转成pdf,再由前端调用接口下载pdf文件! 1、思…...

JMeter---BeanShell实现接口前置和后置操作
在JMeter中,可以使用BeanShell脚本来实现接口的前置和后置操作。 下面是使用BeanShell脚本实现接口前置和后置操作的步骤: 1、在测试计划中添加一个BeanShell前置处理器或后置处理器。 右键点击需要添加前置或后置操作的接口请求,选择&quo…...
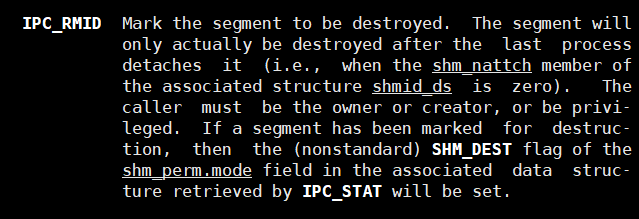
【Linux】共享内存
文章目录 一、共享内存的原理详谈共享内存的实现过程二、共享内存的接口函数1.shmget2. shmatshmdtshmctl 进程间使用共享内存通信三、共享内存的特性 关于代码 一、共享内存的原理 共享内存是由操作系统维护和管理的一块内存。 共享内存的本质是内核级的缓冲区。 一个进程向…...
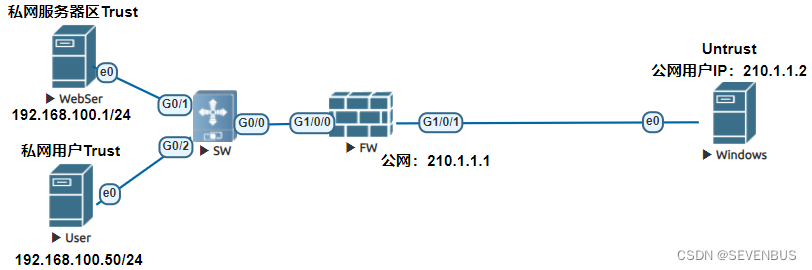
五、双向NAT
学习防火墙之前,对路由交换应要有一定的认识 双向NAT1.1.基本原理1.2.NAT Inbound NAT Server1.3.域内NATNAT Server —————————————————————————————————————————————————— 双向NAT 经过前面介绍,…...
P1028 [NOIP2001 普及组] 数的计算
时刻记住一句话:写递归,1画图,2大脑放空!!! 意思是,自己写递归题目,先用样例给的数据画图,然后想一个超级简单的思路,直接套上去就可以了。 上题干ÿ…...
浅析三相异步电动机控制的电气保护
安科瑞 华楠 摘 要:要求三相异步电动机的控制系统不仅要保证电机正常启动和运行,完成制动操作,还要通过相关保护措施维护电动机的安全使用。基于此,本文以电动机电气保护作为研究对象,结合三相异步电动机的机械特点&…...
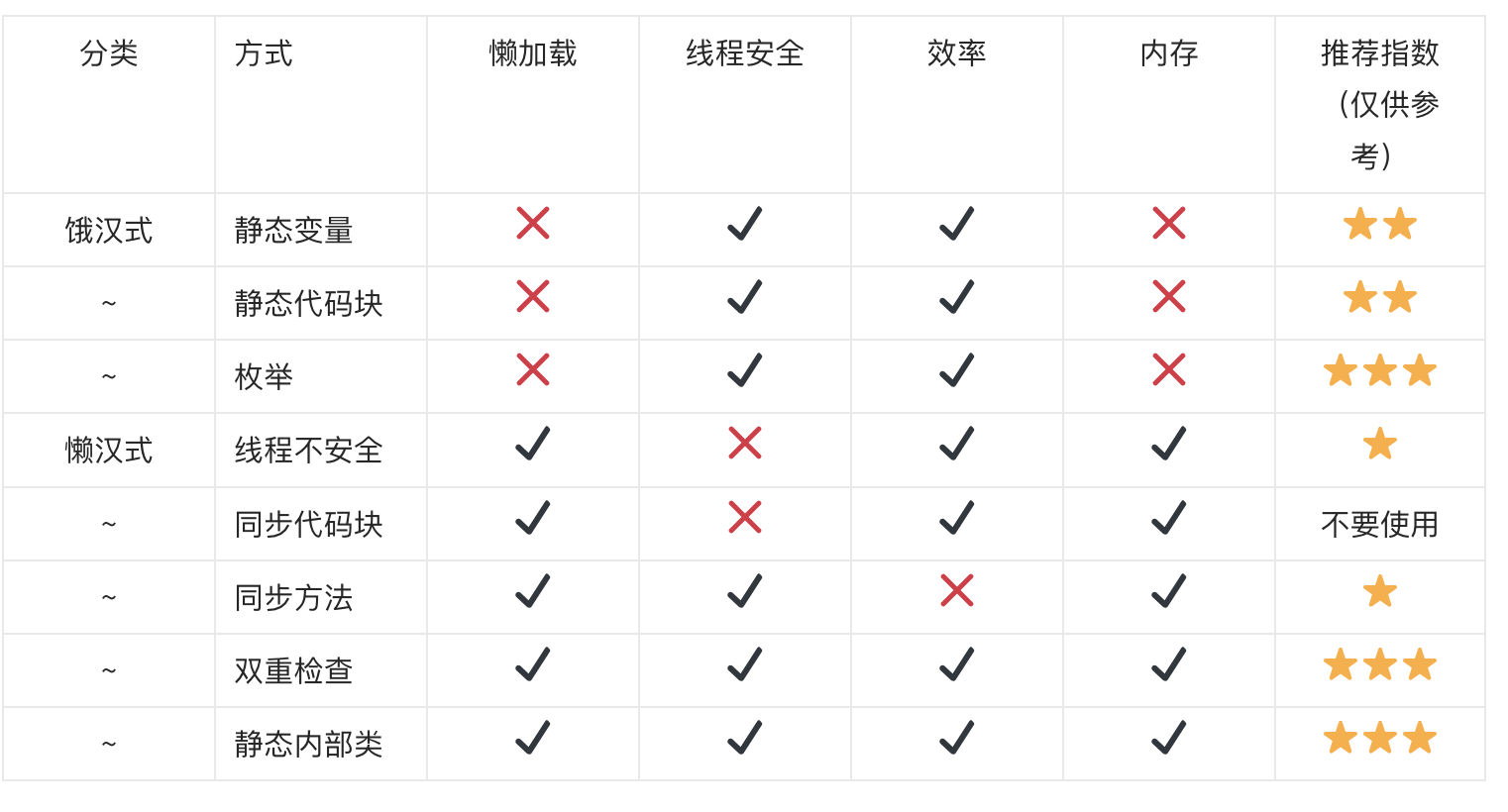
Java设计模式系列:单例设计模式
Java设计模式系列:单例设计模式 介绍 所谓类的单例设计模式,就是采取一定的方法保证在整个的软件系统中,对某个类只能存在一个对象实例,并且该类只提供一个取得其对象实例的方法(静态方法) 比如 Hiberna…...

开拓新天地:探讨数位行销对医药产业医病连结的影响
数字营销模式多元,主要围绕医生和患者。赛道各企业凭借各自优势(技术、学术、流量等)入局,提供各自差异化营销工具或服务。目前,围绕医生的数字营销旨在为医生提供全面学术解决方案从而提升对医药产品的认可࿰…...

[tsai.shen@mailfence.com].faust勒索病毒数据怎么处理|数据解密恢复
导言: [support2022cock.li].faust、[tsai.shenmailfence.com].faust、[Encrypteddmailfence.com].faust勒索病毒是一种具有恶意目的的勒索软件,其主要特点包括对受害者文件进行强力加密,然后勒索受害者支付赎金以获取解密密钥。攻击者通常通…...
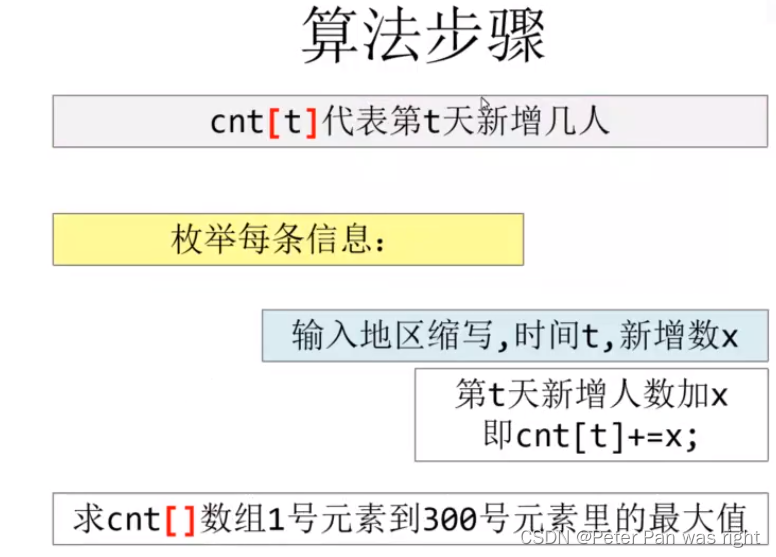
Peter算法小课堂—前缀和数组的应用
桶 相当于计数排序,看一个视频 桶排序 太戈编程1620题 算法解析 #include <bits/stdc.h> using namespace std; const int R11; int cnt[R];//cnt[t]代表第t天新增几人 int s[R];//s[]数组是cnt[]数组的前缀和数组 int n,t; int main(){cin>>n;for(…...

线性表之链式表
文章目录 主要内容一.单链表1.头插法建立单链表代码如下(示例): 2.尾插法建立单链表代码如下(示例): 3.按序号查找结点值代码如下(示例): 4.按值查找表结点代码如下(示例): 5.插入节…...
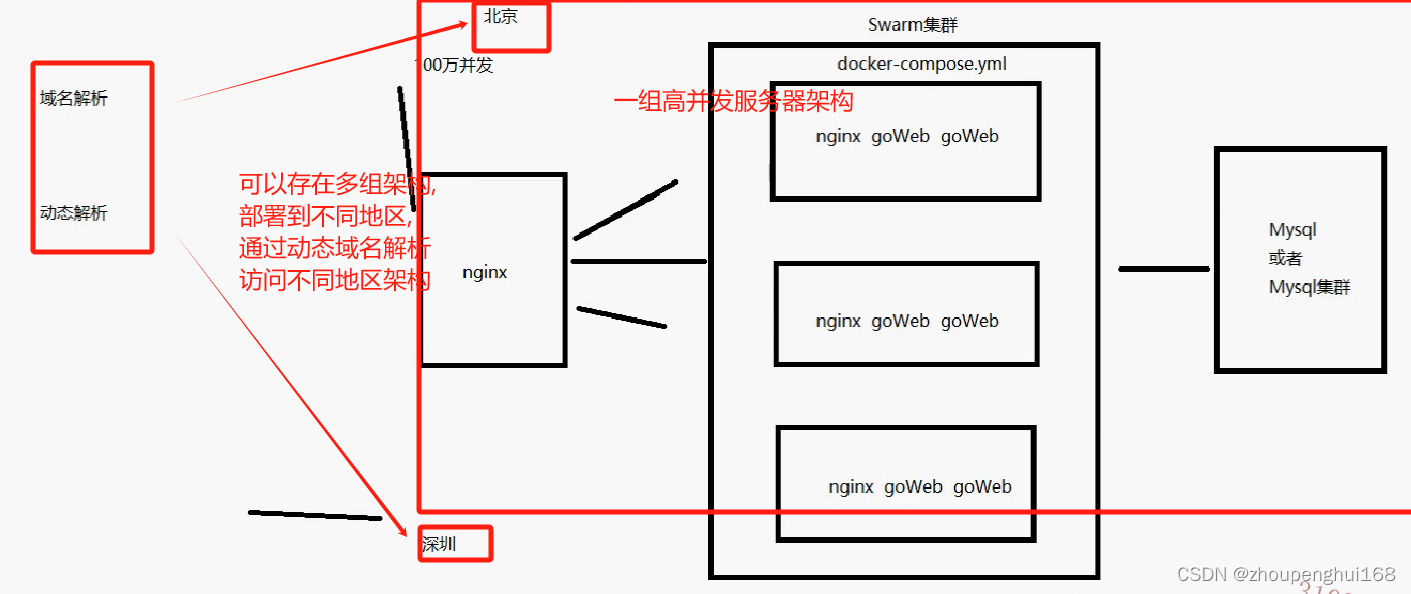
[Docker]十.Docker Swarm讲解
一.Dokcer Swarm集群介绍 1.Dokcer Swarm 简介 Docker Swarm 是 Docker 公司推出的用来管理 docker 集群的工具, 使用 Docker Swarm 可以快速方便的实现 高可用集群 ,Docker Compose 只能编排单节点上的容器, Docker Swarm 可以让我们在单一主机上操作来完成对 整…...

相机机模组需求示例
产品需求名称摄像头采集图片数据补充说明产品需求描述 As:用户 I want to:通过相机模组获取到自定义格式图片数据,要求包括: 1、支持多种场景,如:手持相机拍摄舌苔 2、支持图片分辨率至少达到1920X1080 3、…...

Uniapp 微信登录流程解析
本文将介绍在 Uniapp 应用中实现微信登录的流程,包括准备工作、授权登录、获取用户信息等步骤。 内容大纲: 介绍Uniapp和微信登录: 简要介绍 Uniapp 框架以及微信登录的重要性和流行程度。 准备工作: 注册微信开发者账号创建应用…...
)
红旗Asianux Server Linux V8 安装万里数据库(GreatSQL)
红旗Asianux Server Linux V8 安装万里数据库(GreatSQL) 红旗Asianux介绍: 红旗Asianux Server Linux 8.0是为云时代重新设计的操作系统,为云时代的到来引入了大量新功能,包括用于配置管理、快速迁移框架、编程语言和…...
一文2000字使用JMeter进行接口测试教程!(建议收藏)
安装 使用JMeter的前提需要安装JDK,需要JDK1.7以上版本目前在用的是JMeter5.2版本,大家可自行下载解压使用 运行 进入解压路径如E: \apache-jmeter-5.2\bin,双击jmeter.bat启动运行 启动后默认为英文版本,可通过Options – Cho…...

使用VSCode开发Django指南
使用VSCode开发Django指南 一、概述 Django 是一个高级 Python 框架,专为快速、安全和可扩展的 Web 开发而设计。Django 包含对 URL 路由、页面模板和数据处理的丰富支持。 本文将创建一个简单的 Django 应用,其中包含三个使用通用基本模板的页面。在此…...

C++初阶-list的底层
目录 1.std::list实现的所有代码 2.list的简单介绍 2.1实现list的类 2.2_list_iterator的实现 2.2.1_list_iterator实现的原因和好处 2.2.2_list_iterator实现 2.3_list_node的实现 2.3.1. 避免递归的模板依赖 2.3.2. 内存布局一致性 2.3.3. 类型安全的替代方案 2.3.…...

LeetCode - 394. 字符串解码
题目 394. 字符串解码 - 力扣(LeetCode) 思路 使用两个栈:一个存储重复次数,一个存储字符串 遍历输入字符串: 数字处理:遇到数字时,累积计算重复次数左括号处理:保存当前状态&a…...
【机器视觉】单目测距——运动结构恢复
ps:图是随便找的,为了凑个封面 前言 在前面对光流法进行进一步改进,希望将2D光流推广至3D场景流时,发现2D转3D过程中存在尺度歧义问题,需要补全摄像头拍摄图像中缺失的深度信息,否则解空间不收敛…...

什么是库存周转?如何用进销存系统提高库存周转率?
你可能听说过这样一句话: “利润不是赚出来的,是管出来的。” 尤其是在制造业、批发零售、电商这类“货堆成山”的行业,很多企业看着销售不错,账上却没钱、利润也不见了,一翻库存才发现: 一堆卖不动的旧货…...

微服务商城-商品微服务
数据表 CREATE TABLE product (id bigint(20) UNSIGNED NOT NULL AUTO_INCREMENT COMMENT 商品id,cateid smallint(6) UNSIGNED NOT NULL DEFAULT 0 COMMENT 类别Id,name varchar(100) NOT NULL DEFAULT COMMENT 商品名称,subtitle varchar(200) NOT NULL DEFAULT COMMENT 商…...

UR 协作机器人「三剑客」:精密轻量担当(UR7e)、全能协作主力(UR12e)、重型任务专家(UR15)
UR协作机器人正以其卓越性能在现代制造业自动化中扮演重要角色。UR7e、UR12e和UR15通过创新技术和精准设计满足了不同行业的多样化需求。其中,UR15以其速度、精度及人工智能准备能力成为自动化领域的重要突破。UR7e和UR12e则在负载规格和市场定位上不断优化…...

[Java恶补day16] 238.除自身以外数组的乘积
给你一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法,且在 O(n) 时间复杂度…...

学习STC51单片机32(芯片为STC89C52RCRC)OLED显示屏2
每日一言 今天的每一份坚持,都是在为未来积攒底气。 案例:OLED显示一个A 这边观察到一个点,怎么雪花了就是都是乱七八糟的占满了屏幕。。 解释 : 如果代码里信号切换太快(比如 SDA 刚变,SCL 立刻变&#…...

推荐 github 项目:GeminiImageApp(图片生成方向,可以做一定的素材)
推荐 github 项目:GeminiImageApp(图片生成方向,可以做一定的素材) 这个项目能干嘛? 使用 gemini 2.0 的 api 和 google 其他的 api 来做衍生处理 简化和优化了文生图和图生图的行为(我的最主要) 并且有一些目标检测和切割(我用不到) 视频和 imagefx 因为没 a…...
