【数据结构】—搜索二叉树(C++实现,超详细!)

🎬慕斯主页:修仙—别有洞天
♈️今日夜电波:消えてしまいそうです—真夜中
1:15━━━━━━️💟──────── 4:18
🔄 ◀️ ⏸ ▶️ ☰
💗关注👍点赞🙌收藏您的每一次鼓励都是对我莫大的支持😍
目录
一、二叉搜索树概念
什么是二叉搜索树?
二叉搜索树的基本操作
二、二叉搜索树的实现
节点的定义
二叉搜索树的定义
非递归操作
插入操作
查找操作
删除操作(重点及难点!!!)
递归法操作
中序遍历排升序(经典操作!)
插入操作(递归)
查找操作(递归)
删除操作(递归)
二叉搜索树的应用
KV模型二叉搜索树
三、整体代码
一、二叉搜索树概念
什么是二叉搜索树?
二叉搜索树(Binary Search Tree,BST)是一种特殊的二叉树,它满足以下几个条件:
- 左子树中所有节点的值小于当前节点的值。
- 右子树中所有节点的值大于当前节点的值。
- 左子树和右子树也都是二叉搜索树。
二叉搜索树的中序遍历可以得到一个升序的序列,因此它常被用来实现有序集合或映射。在二叉搜索树中,查找、插入和删除操作的时间复杂度通常为O(logn),其中n为树中节点的数量,这得益于二叉搜索树的结构和查找方法。
如下便是一颗二叉搜索树:
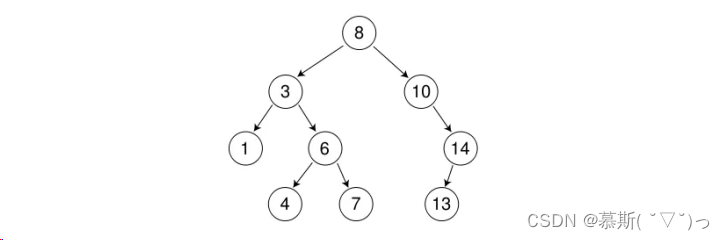
一句话总结二叉搜索树:
左子树节点总是比父节点小,右子树节点总是比父节点大的二叉树。
二叉搜索树的基本操作
利用二叉搜索树特性排升序。一听到二叉树,我们通常会想到的是什么?递归!请细细想想我们二叉搜索树的特点->左边的节点总是比父节点小,右边的节点总是比父节点大!那么我们对它使用中序遍历会发生什么呢?还是上面的那颗二叉树,对他进行中序遍历后:
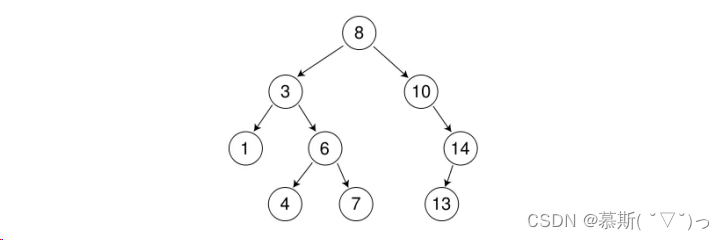
中序遍历结果:arr={1,3,4,6,7,8,10,13,14};
二、二叉搜索树的实现
节点的定义
说来惭愧作者在此前实现数据结构都是用C语言实现的 o (╥﹏╥)o. ,本文应该是作为作者第一篇用C++实现的数据结构,也算是一个新的起点吧!
与C语言的区别主要还是在于在此使用struct(实际上是类)可以在定义时就进行初始化,利用的就是类的初始化列表的作用,这就省去了我们C语言时需要额外定义以及调用的初始化操作。只能说有了C++,C语言什么的不认识啦ʅ(´◔౪◔)ʃ
//节点定义template<class K>struct BSTreeNode{BSTreeNode<K>* _left;BSTreeNode<K>* _right;K _key;BSTreeNode(const K& key):_left(nullptr), _right(nullptr), _key(key){}};二叉搜索树的定义
对于节点实例化并且重命名,并且给数据进行缺省赋值。
//二叉搜索树template<class K>class BSTree{typedef BSTreeNode<K> Node;public://...诸多的操作private:Node* _root = nullptr;};非递归操作
插入操作
插入的具体过程如下:
a. 树为空,则直接新增节点,赋值给root指针
b. 树不空,按二叉搜索树性质查找插入位置,插入新节点
思路:判断是否为空->是-》直接给根节点赋值->否->进行循环遍历对要插入的值进行“比大小”->大往右,小往左遍历,直到空为止->比较空位置父节点的大小,大插右,小插左
//插入操作,按照左小右大的规则bool Insert(const K& key){if (_root == nullptr){_root = new Node(key);return true;}Node* parent = nullptr;Node* cur = _root;while (cur){parent = cur;if (cur->_key < key){cur = cur->_right;}else if (cur->_key > key){cur = cur->_left;}else{return false;}}cur = new Node(key);if (parent->_key < key){parent->_right = cur;}else{parent->_left = cur;}return true;}查找操作
通过搜索二叉树的特性,通过比较大小即可完成查找。
//查找操作bool Find(const K& key){Node* cur = _root;while (cur){if (cur->_key < key){cur = cur->_right;}else if (cur->_key > key){cur = cur->_left;}else{return true;}}return false;}删除操作(重点及难点!!!)
首先查找元素是否在二叉搜索树中,如果不存在,则返回, 否则要删除的结点可能分下面四种情况:
a. 要删除的结点无孩子结点
b. 要删除的结点只有左孩子结点
c. 要删除的结点只有右孩子结点
d. 要删除的结点有左、右孩子结点
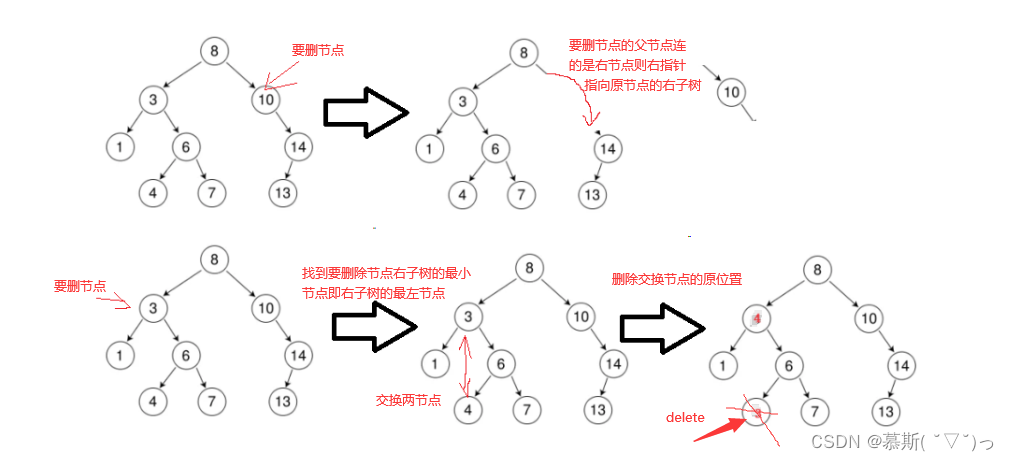
看起来有待删除节点有4中情况,实际情况a可以与情况b或者c合并起来,因此真正的删除过程如下:
情况b:删除该结点且使被删除节点的双亲结点指向被删除节点的左孩子结点--直接删除
情况c:删除该结点且使被删除节点的双亲结点指向被删除结点的右孩子结点--直接删除
情况d:在它的右子树中寻找中序下的第一个结点(关键码最小),用它的值填补到被删除节点中,再来处理该结点的删除问题--替换法删除
而在b、c、d这三种情况中,b和c又很相似,所以以大类来划分,我们实际可以分为两种。一种是要删除的节点只有一个左孩子或者右孩子,另一种是有两个孩子节点。
现在详细介绍这两种情况:
当只有一个孩子节点时: 当要删节点的左孩子为空时,我们只需要将右半边给他的父亲就行,当然我们也需要注意以下两点:1、如果要删节点是根节点,那么我们需要将它的右孩子的地址覆盖原节点。2、要删节点不是根节点,那么我们也需要判断要删节点是它父节点的左孩子还是右孩子;左孩子则父节点的左孩子节点指向要删孩子的右孩子,右孩子则父节点的右孩子节点指向要删孩子的右孩子。当要删右孩子时也是同理,只是需要注意此时要注意的第二点中要指向的是要删节点是右孩子。下面上半部分的图为此部分的图解~
当有两个孩子节点时:我们则需要用到替换法。首先,我们需要根据以下规则中的一个规则:1、找到要删节点的左子树的最大节点。2、找到要删奇点的右子树的最小节点。接着,交换要删节点和找到的这个节点。最后,删除找到节点的位置,这个时候,我们就需要返回到上一部分我们只有一个孩子节点时要走的步骤,进行相应的操作。为什么呢?因为我们都知道要找最小或者最大只有在最左或者最右。而此时我们一定满足只有一个孩子节点时的于要求。下面下半部分的图为此部分的图解,这里取右子树的最小~
实现如下:
bool Erase(const K& key){Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_key < key){parent = cur;cur = cur->_right;}else if (cur->_key > key){parent = cur;cur = cur->_left;}else//表示已经找到,进行删除操作{//左为空的情况if (cur->_left == nullptr){if (cur == _root)//要删即为根节点{_root = cur->_right;}else{if (cur == parent->_left)//因为左一定为空,为父节点的左则将右半边给父即可{parent->_left = cur->_right;}else//同理为父节点的右则将右半边给父{parent->_right = cur->_right;}}delete cur;}else if (cur->_right == nullptr)//右为空的情况{//同理左为空if (cur == _root){_root = cur->_left;}else{if (cur == parent->_left){parent->_left = cur->_left;}else{parent->_right = cur->_left;}}delete cur;}else//左右都不为空{//可以选择找该节点左子树的最大节点(最右节点)或者右子树的最小节点(最左节点)//这里找右树的最小节点(最左节点)Node* parent = cur;Node* subleft = cur->_right;while (subleft->_left){parent = subleft;subleft = subleft->_left;}swap(cur->_key, subleft->_key);//由于找到的是最左,则默认左为空,所以只需将右链接给父节点if (subleft == parent->_left){parent->_left = subleft->_right;}else{parent->_right = subleft->_right;}delete subleft;}return true;}}return false;}
递归法操作
中序遍历排升序(经典操作!)
上面详细介绍过了,不多阐述~
void _InOrder(Node* root){if (root == nullptr)return;_InOrder(root->_left);cout << root->_key << " ";_InOrder(root->_right);}插入操作(递归)
实际上同非递归的原理是相同的,不多阐述。实在不行画递归展开图就理解了~
bool _InsertR(Node*& root, const K& key){if (root == nullptr){root = new Node(key);return true;}if (root->_key < key)return _InsertR(root->_right, key);else if (root->_key > key)return _InsertR(root->_left, key);elsereturn false;}查找操作(递归)
bool _FindR(Node* root, const K& key){if (root == nullptr){return false;}if (root->_key < key){return _FindR(root->_right, key);}else if (root->_key > key){return _FindR(root->_left, key);}else{return true;}}删除操作(递归)
实际上操作同非递归是一致的 ,特别注意接口的对于root的引用,这对于后续删除很有作用。当要删除只有一个孩子节点的节点时,同非递归的思想是一样的。当要删节点有两个孩子节点时,在最后面采取的是装换成在子树中去删除,同非递归中的找到替换节点转到只有一个孩子的操作是一样的思想。
bool _EraseR(Node*& root, const K& key){if (root == nullptr)return false;if (root->_key < key){return _EraseR(root->_right, key);}else if (root->_key > key){return _EraseR(root->_left, key);}else//找到了开始删除{//实际上的操作同非递归差不多,这里巧妙的对root运用了引用if (root->_left == nullptr){Node* del = root;root = root->_right;delete del;return true;}else if (root->_right == nullptr){Node* del = root;root = root->_left;delete del;return true;}else//找右子树的最大{Node* subleft = root->_right;while (subleft->_left){subleft = subleft->_left;}swap(root->_key, subleft->_key);// 转换成在子树去递归删除return _EraseR(root->_right, key);}}}二叉搜索树的应用
以上我们实现的二叉搜索树实际上也被称为K模型,而实际上还有一种模型叫做KV模型,以下为详细介绍:
1. K模型:K模型即只有key作为关键码,结构中只需要存储Key即可,关键码即为需要搜索到的值。比如:给一个单词word,判断该单词是否拼写正确,具体方式如下:
以词库中所有单词集合中的每个单词作为key,构建一棵二叉搜索树
在二叉搜索树中检索该单词是否存在,存在则拼写正确,不存在则拼写错误。
2. KV模型:每一个关键码key,都有与之对应的值Value,即<Key, Value>的键值对。该种方式在现实生活中非常常见:比如
英汉词典就是英文与中文的对应关系,通过英文可以快速找到与其对应的中文,英文单词与其对应的中文<word, chinese>就构成一种键值对;
再比如统计单词次数,统计成功后,给定单词就可快速找到其出现的次数,单词与其出现次数就是<word, count>就构成一种键值对
KV模型二叉搜索树
KV模型实际上同K模型差不多, 只是在K模型的基础上加了一个value值,对于其它的操作都是相似的,以下给出KV模型的整体代码:
namespace kv
{template<class K, class V>struct BSTreeNode{BSTreeNode<K, V>* _left;BSTreeNode<K, V>* _right;K _key;V _value;BSTreeNode(const K& key, const V& value):_left(nullptr), _right(nullptr), _key(key), _value(value){}};template<class K, class V>class BSTree{typedef BSTreeNode<K, V> Node;public:bool Insert(const K& key, const V& value){if (_root == nullptr){_root = new Node(key, value);return true;}Node* parent = nullptr;Node* cur = _root;while (cur){parent = cur;if (cur->_key < key){cur = cur->_right;}else if (cur->_key > key){cur = cur->_left;}else{return false;}}cur = new Node(key, value);if (parent->_key < key){parent->_right = cur;}else{parent->_left = cur;}return true;}Node* Find(const K& key){Node* cur = _root;while (cur){if (cur->_key < key){cur = cur->_right;}else if (cur->_key > key){cur = cur->_left;}else{return cur;}}return nullptr;}bool Erase(const K& key){Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_key < key){parent = cur;cur = cur->_right;}else if (cur->_key > key){parent = cur;cur = cur->_left;}else{// 准备删除 20:15继续if (cur->_left == nullptr){//左为空if (cur == _root){_root = cur->_right;}else{if (cur == parent->_left){parent->_left = cur->_right;}else{parent->_right = cur->_right;}}}else if (cur->_right == nullptr){//右为空if (cur == _root){_root = cur->_left;}else{if (cur == parent->_left){parent->_left = cur->_left;}else{parent->_right = cur->_left;}}}else{//左右都不为空// 右树的最小节点(最左节点)Node* parent = cur;Node* subLeft = cur->_right;while (subLeft->_left){parent = subLeft;subLeft = subLeft->_left;}swap(cur->_key, subLeft->_key);if (subLeft == parent->_left)parent->_left = subLeft->_right;elseparent->_right = subLeft->_right;}return true;}}return false;}void InOrder(){_InOrder(_root);cout << endl;}private:void _InOrder(Node* root){if (root == nullptr)return;_InOrder(root->_left);cout << root->_key << ":" << root->_value << endl;_InOrder(root->_right);}private:Node* _root = nullptr;};}三、整体代码
#pragma once
#include<iostream>
using namespace std;namespace K
{//节点定义template<class K>struct BSTreeNode{BSTreeNode<K>* _left;BSTreeNode<K>* _right;K _key;BSTreeNode(const K& key):_left(nullptr), _right(nullptr), _key(key){}};//二叉搜索树template<class K>class BSTree{typedef BSTreeNode<K> Node;public://插入操作,按照左小右大的规则bool Insert(const K& key){if (_root == nullptr){_root = new Node(key);return true;}Node* parent = nullptr;Node* cur = _root;while (cur){parent = cur;if (cur->_key < key){cur = cur->_right;}else if (cur->_key > key){cur = cur->_left;}else{return false;}}cur = new Node(key);if (parent->_key < key){parent->_right = cur;}else{parent->_left = cur;}return true;}//查找操作bool Find(const K& key){Node* cur = _root;while (cur){if (cur->_key < key){cur = cur->_right;}else if (cur->_key > key){cur = cur->_left;}else{return true;}}return false;}bool Erase(const K& key){Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_key < key){parent = cur;cur = cur->_right;}else if (cur->_key > key){parent = cur;cur = cur->_left;}else//表示已经找到,进行删除操作{//左为空的情况if (cur->_left == nullptr){if (cur == _root)//要删即为根节点{_root = cur->_right;}else{if (cur == parent->_left)//因为左一定为空,为父节点的左子树则将右半边给父即可{parent->_left = cur->_right;}else//同理为父节点的右则将右半边给父{parent->_right = cur->_right;}}delete cur;}else if (cur->_right == nullptr)//右为空的情况{//同理左为空if (cur == _root){_root = cur->_left;}else{if (cur == parent->_left){parent->_left = cur->_left;}else{parent->_right = cur->_left;}}delete cur;}else//左右都不为空{//可以选择找该节点左子树的最大节点(最右节点)或者右子树的最小节点(最左节点)//这里找右树的最小节点(最左节点)Node* parent = cur;Node* subleft = cur->_right;while (subleft->_left){parent = subleft;subleft = subleft->_left;}swap(cur->_key, subleft->_key);//由于找到的是最左,则默认左为空,所以只需将右链接给父节点if (subleft == parent->_left){parent->_left = subleft->_right;}else{parent->_right = subleft->_right;}delete subleft;}return true;}}return false;}void InOrder()//中序遍历即排升序{_InOrder(_root);cout << endl;}bool FindR(const K& key)//递归找{return _FindR(_root, key);}bool InsertR(const K& key)//递归插入{return _InsertR(_root, key);}bool EraseR(const K& key)//递归删{return _EraseR(_root, key);}BSTree() = default;// C++11~BSTree(){Destroy(_root);}BSTree(const BSTree<K>& t){_root = Copy(t._root);}// t1 = t3BSTree<K>& operator=(BSTree<K> t){swap(_root, t._root);return *this;}private:Node* Copy(Node* root){if (root == nullptr)return nullptr;Node* newRoot = new Node(root->_key);newRoot->_left = Copy(root->_left);newRoot->_right = Copy(root->_right);return newRoot;}void Destroy(Node*& root){if (root == nullptr)return;Destroy(root->_left);Destroy(root->_right);delete root;root = nullptr;}bool _EraseR(Node*& root, const K& key){if (root == nullptr)return false;if (root->_key < key){return _EraseR(root->_right, key);}else if (root->_key > key){return _EraseR(root->_left, key);}else//找到了开始删除{//实际上的操作同非递归差不多,这里巧妙的对root运用了引用if (root->_left == nullptr){Node* del = root;root = root->_right;delete del;return true;}else if (root->_right == nullptr){Node* del = root;root = root->_left;delete del;return true;}else//找右子树的最大{Node* subleft = root->_right;while (subleft->_left){subleft = subleft->_left;}swap(root->_key, subleft->_key);// 转换成在子树去递归删除return _EraseR(root->_right, key);}}}bool _InsertR(Node*& root, const K& key){if (root == nullptr){root = new Node(key);return true;}if (root->_key < key)return _InsertR(root->_right, key);else if (root->_key > key)return _InsertR(root->_left, key);elsereturn false;}bool _FindR(Node* root, const K& key){if (root == nullptr){return false;}if (root->_key < key){return _FindR(root->_right, key);}else if (root->_key > key){return _FindR(root->_left, key);}else{return true;}}void _InOrder(Node* root){if (root == nullptr)return;_InOrder(root->_left);cout << root->_key << " ";_InOrder(root->_right);}Node* _root = nullptr;};
}namespace kv
{template<class K, class V>struct BSTreeNode{BSTreeNode<K, V>* _left;BSTreeNode<K, V>* _right;K _key;V _value;BSTreeNode(const K& key, const V& value):_left(nullptr), _right(nullptr), _key(key), _value(value){}};template<class K, class V>class BSTree{typedef BSTreeNode<K, V> Node;public:bool Insert(const K& key, const V& value){if (_root == nullptr){_root = new Node(key, value);return true;}Node* parent = nullptr;Node* cur = _root;while (cur){parent = cur;if (cur->_key < key){cur = cur->_right;}else if (cur->_key > key){cur = cur->_left;}else{return false;}}cur = new Node(key, value);if (parent->_key < key){parent->_right = cur;}else{parent->_left = cur;}return true;}Node* Find(const K& key){Node* cur = _root;while (cur){if (cur->_key < key){cur = cur->_right;}else if (cur->_key > key){cur = cur->_left;}else{return cur;}}return nullptr;}bool Erase(const K& key){Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_key < key){parent = cur;cur = cur->_right;}else if (cur->_key > key){parent = cur;cur = cur->_left;}else{// 准备删除 20:15继续if (cur->_left == nullptr){//左为空if (cur == _root){_root = cur->_right;}else{if (cur == parent->_left){parent->_left = cur->_right;}else{parent->_right = cur->_right;}}}else if (cur->_right == nullptr){//右为空if (cur == _root){_root = cur->_left;}else{if (cur == parent->_left){parent->_left = cur->_left;}else{parent->_right = cur->_left;}}}else{//左右都不为空// 右树的最小节点(最左节点)Node* parent = cur;Node* subLeft = cur->_right;while (subLeft->_left){parent = subLeft;subLeft = subLeft->_left;}swap(cur->_key, subLeft->_key);if (subLeft == parent->_left)parent->_left = subLeft->_right;elseparent->_right = subLeft->_right;}return true;}}return false;}void InOrder(){_InOrder(_root);cout << endl;}private:void _InOrder(Node* root){if (root == nullptr)return;_InOrder(root->_left);cout << root->_key << ":" << root->_value << endl;_InOrder(root->_right);}private:Node* _root = nullptr;};}感谢你耐心的看到这里ღ( ´・ᴗ・` )比心,如有哪里有错误请踢一脚作者o(╥﹏╥)o!

给个三连再走嘛~
相关文章:

【数据结构】—搜索二叉树(C++实现,超详细!)
🎬慕斯主页:修仙—别有洞天 ♈️今日夜电波:消えてしまいそうです—真夜中 1:15━━━━━━️💟──────── 4:18 🔄 ◀️ ⏸ ▶️…...
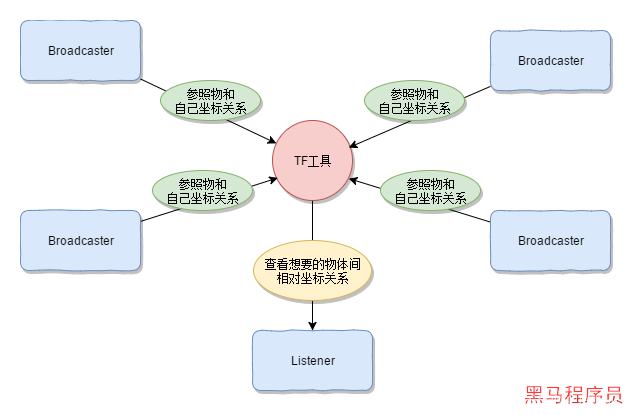
机器人算法—ROS TF坐标变换
1.TF基本概念 (1)什么是TF? TF是Transformations Frames的缩写。在ROS中,是一个工具包,提供了坐标转换等方面的功能。 tf工具包,底层实现采用的是一种树状数据结构,根据时间缓冲并维护多个参考…...
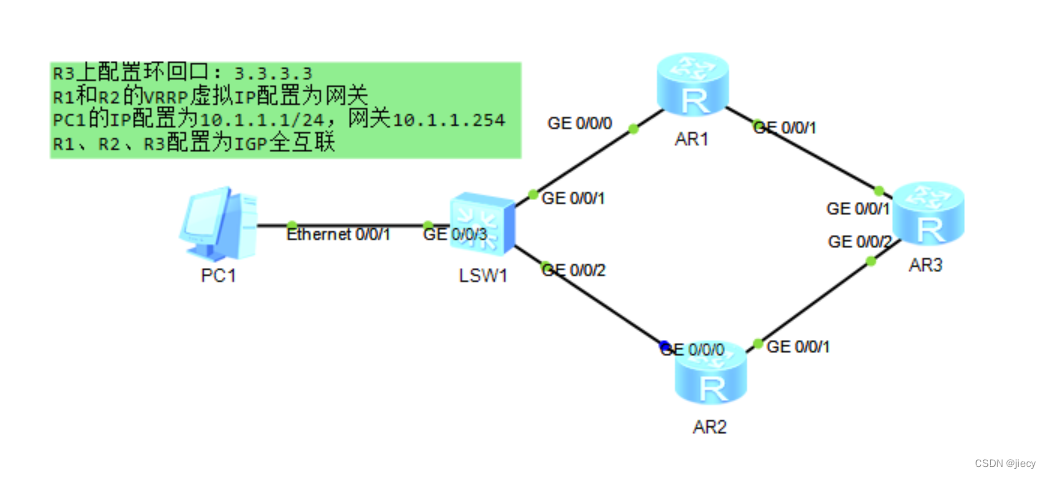
路由VRRP配置例子
拓朴如下: 主要配置如下: [R1] interface GigabitEthernet0/0/0ip address 10.1.1.1 255.255.255.0 vrrp vrid 1 virtual-ip 10.1.1.254vrrp vrid 1 priority 200vrrp vrid 1 preempt-mode timer delay 20 # interface GigabitEthernet0/0/1ip address …...
)
OpenGL 绘制点与三角形(Qt)
文章目录 一、简介二、实现代码三、实现效果一、简介 这里对OpenGL中点与三角形相关绘制操作进行封装,方便后续点云数据与模型数据的渲染。 二、实现代码 这里我们先创建一个基类Drawable,后续的点、线、面等,均会继承该类: Drawable.h #ifndef DRAWABLE_H #define DRAWABL…...

究竟什么是阻塞与非阻塞、同步与异步
文章目录 前言阻塞与非阻塞同步与异步复杂的网络IO真正的异步IOIO分类与示例总结 前言 这几个名词在程序开发时经常听到,但是突然问起来各个词的含义一时间还真是说不清楚,貌似这几个词都是翻译过来的,每个人的解释都不太一样,我…...
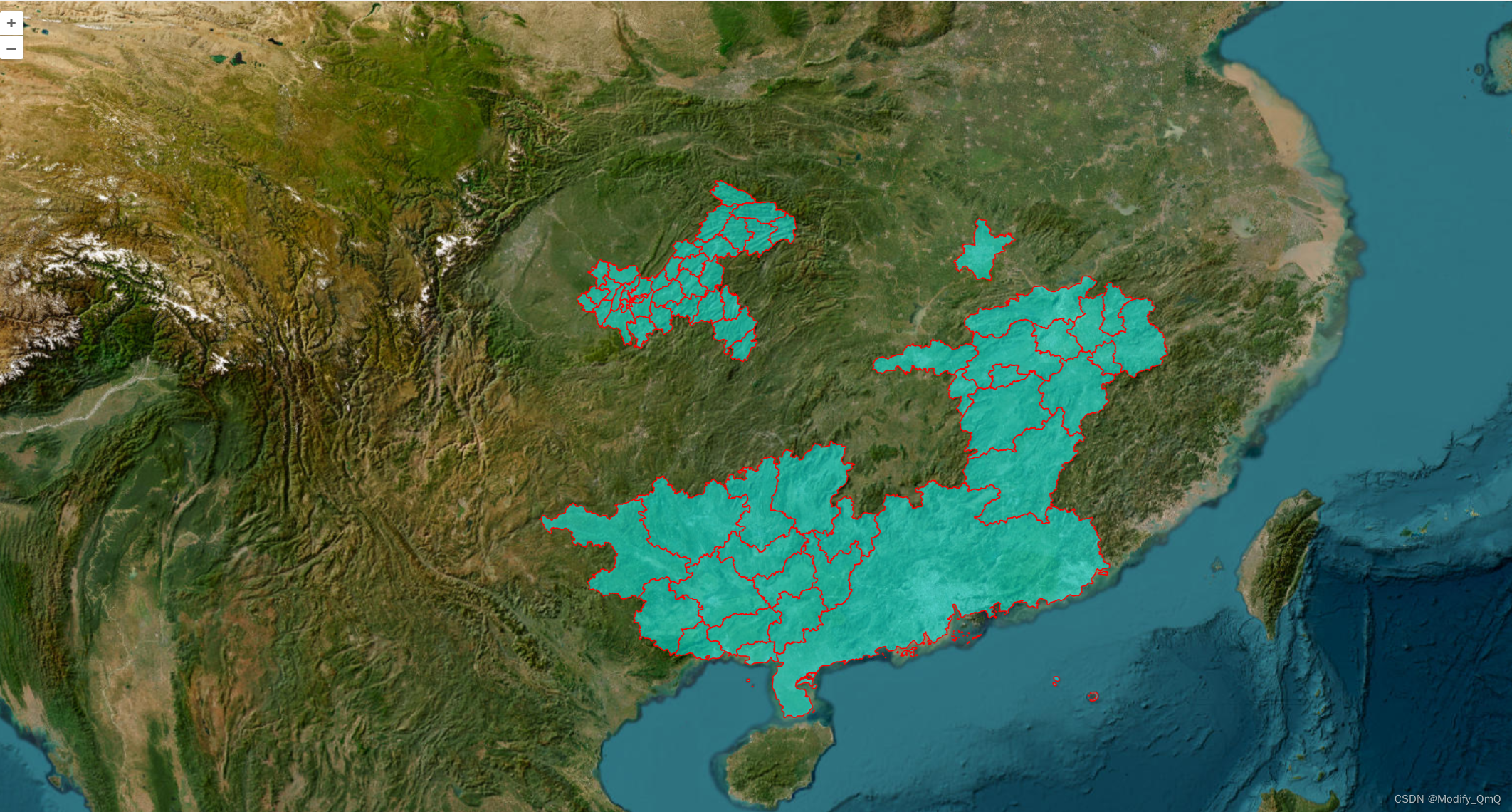
Openlayer【三】—— 绘制多边形GeoJson边界绘制
1.1、绘制多边形 在绘制多边形和前面绘制线有异曲同工之妙,多边形本质上就是由多个点组成的线然后连接组成的面,这个面就是最终的结果,那么这里使用到的是Polygon对象,而传给这个对象的值也是多个坐标,坐标会一个个的…...
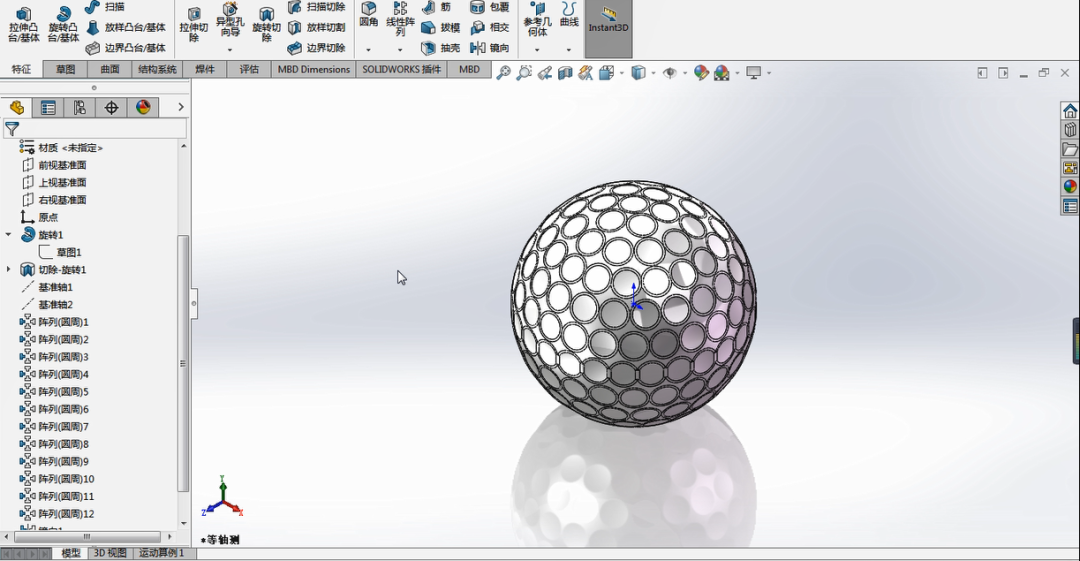
用SOLIDWORKS画个高尔夫球,看似简单的建模却大有学问
SOLIDWORKS软件提供了大量的建模功能,如果工程师能灵活使用这些功能,就可以绘制得到各式各样的模型,我们尝试使用SOLIDWORKS绘制高尔夫球模型,如下图所示。 为什么选用solid works进行建模? solid works是一款功能强大…...

Linux:Network: ARP被动删除的一个情况
今天看到Linux内核里arp代码相关的一个函数,让人想起来很久之前掉进去的一个坑。 说产品的实现里,会存放一个dummy的neighbor(arp记录)在系统里,然后根据这个dummy的记录做一些特殊的处理。 但是当时根本就不知道这个记录的存在,也就无从谈起说要在做设计时考虑它的存在。…...
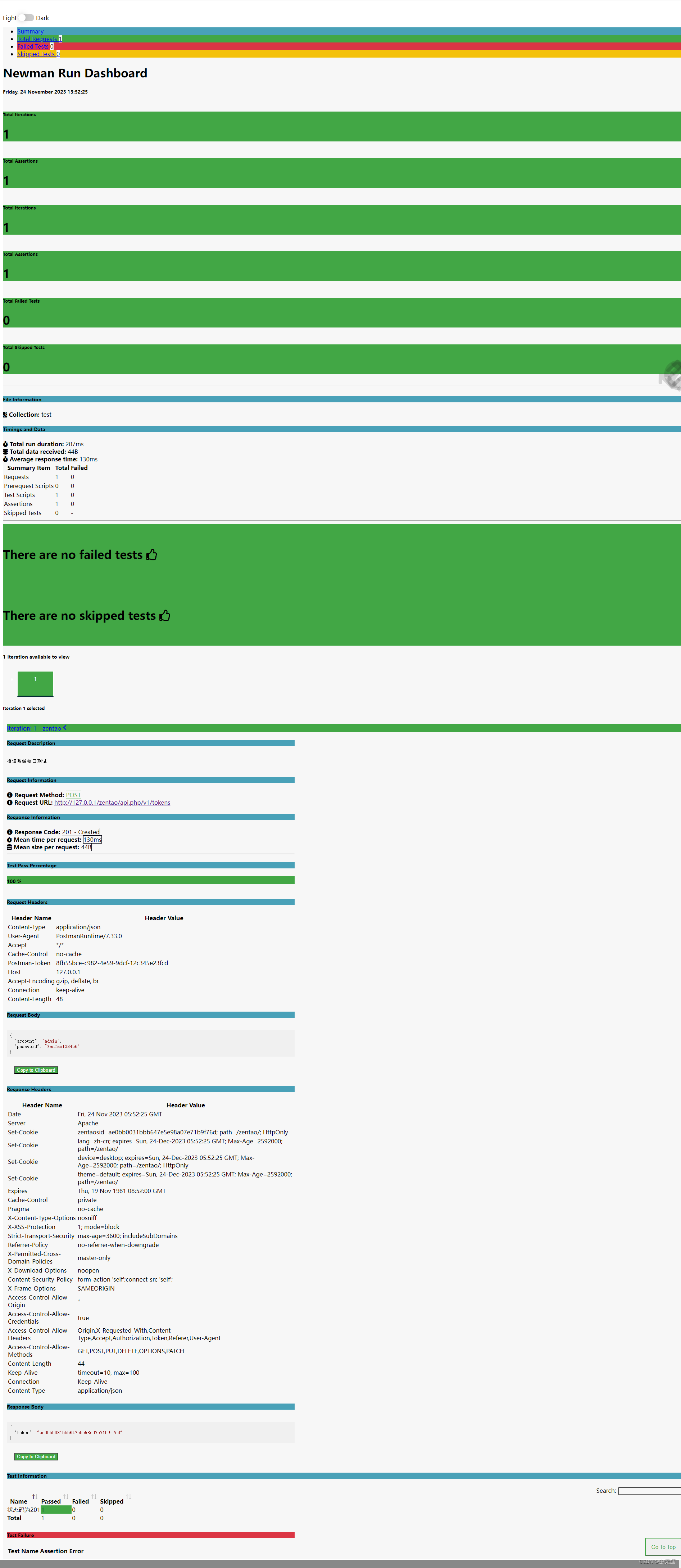
『接口测试干货』| Newman+Postman接口自动化测试完整过程
『接口测试干货』| NewmanPostman接口自动化测试完整过程 1 Newman简介2 如何安装Newman?2.1 安装NodeJs2.2 安装Newman2.2 解决Newman不是内部命令 3 Newman使用3.1 Newman如何运行集合?3.2 如何查看帮助文档?3.3 环境变量设置3.4 关于全局变…...
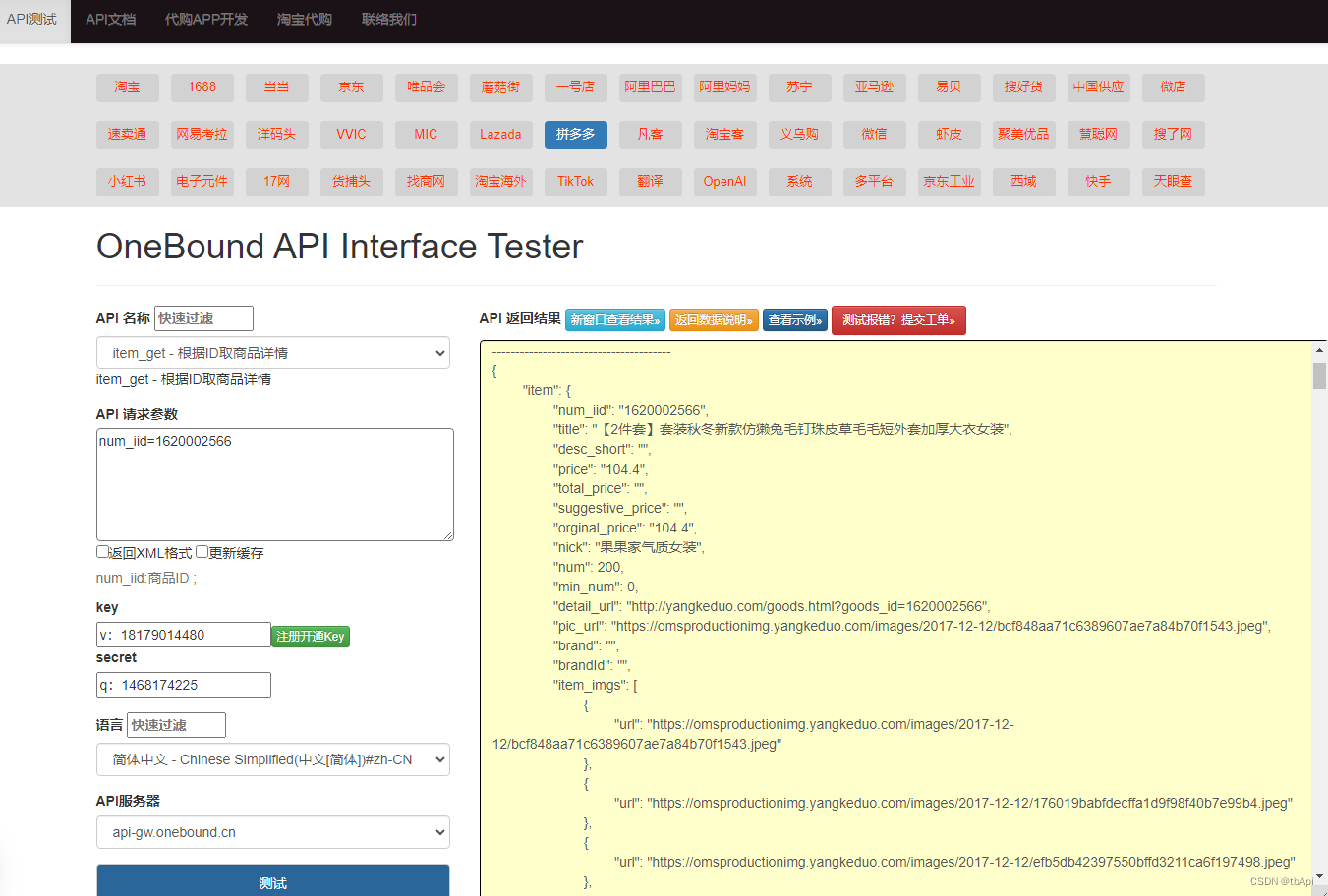
根据商品链接获取拼多多商品详情数据接口|拼多多商品详情价格数据接口|拼多多API接口
拼多多,作为中国最大的社交电商之一,为卖家提供了丰富的商品详情接口。这些接口可以帮助卖家快速获取商品信息,提高销售效率。本文将详细介绍如何使用拼多多商品详情接口,以及它的优势和注意事项。 一、拼多多商品详情接口概述 …...

KaiwuDB 监控组件及辅助 SQL 调优介绍
一、介绍 KaiwuDB 具备完善的行为数据采集功能,此功能要求 KaiwuDB 数据库系统 C/E/T 端不同进程的不同维度的指标采集功能十分完善;在不同进程完成指标采集后,会通过 Opentelemetry 和 Collector 将指标存入 Prometheus,以便查找…...
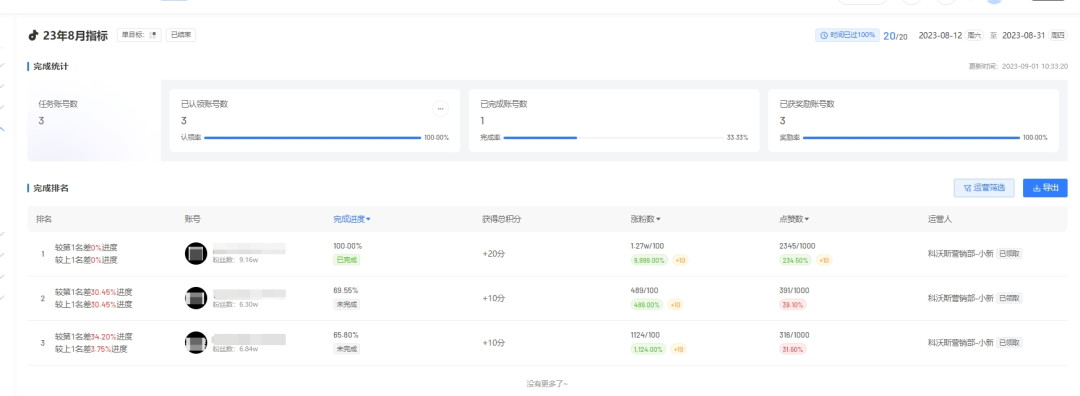
双11再创新高!家电行业如何通过矩阵管理,赋能品牌增长?
双11大促已落下帷幕,虽然今年不再战报满天飞,但从公布的数据来看,家电行业整体表现不俗。 根据抖音电商品牌业务发布的收官战报,家电行业创造了成交新纪录,整体同比增长125%。快手官方数据显示,消电家居行业…...

苏东坡最经典的诗词
苏东坡最经典的诗词_诗词_百度汉语 水调歌头明月几时有 [作者] 苏轼 [朝代] 宋 丙辰中秋,欢饮达旦,大醉,作此篇,兼怀子由。明月几时有?把酒问青天。不知天上宫阙,今夕是何年。我欲乘风归去,又…...

iterator遍历赋值
在Java中,迭代器(Iterator)是用于遍历集合的对象。它提供了一种顺序访问集合元素的方式,但是不能直接用于给特定索引赋值。 迭代器只能用于遍历集合并访问集合中的元素,而不能通过迭代器来修改集合元素的值。如果你想…...

【从删库到跑路】MySQL数据库 — E-R图 | 关系模型
🎊专栏【MySQL】 🍔喜欢的诗句:更喜岷山千里雪 三军过后尽开颜。 🎆音乐分享【如愿】 大一同学小吉,欢迎并且感谢大家指出我的问题🥰 文章目录 🌹简述什么是E-R图⭐核心概念 🌹E-R图…...

网工内推 | 美的、得力集团,包吃包住,IE认证优先,14薪
01 美的 招聘岗位:网络工程师 职责描述: 1.负责IT网络设备、IDC机房的日常维护巡检、监控和管理; 2.负责路由、交换、防火墙、无线控制器、AP等网络设备的开通、调整、优化升级; 3.负责公司OT、IT网络规划,项目实施以…...
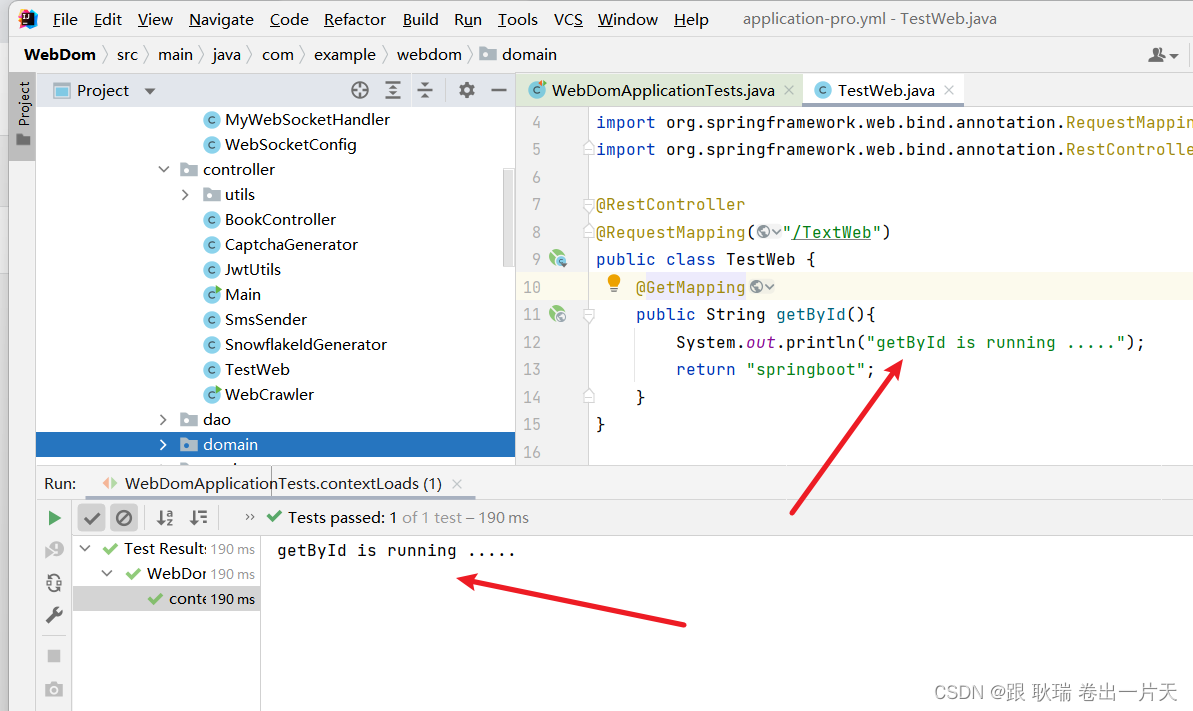
java springboot在测试类中构建虚拟MVC环境并发送请求
好 上文java springboot在测试类中启动一个web环境我们在测试类中搭了一个web环境 那么 下面就要想办法弄一个接口的测试 这边 我们还是要在controller包下去创建一个 controller类 写一个访问接口 这里 我创建一个 TestWeb.java 这里 我们编写代码如下 package com.example.…...

python运算符重载之字符串显示和右侧加法
1 python运算符重载之字符串显示和右侧加法 1.1 重载字符串显示 1.1.1 str和repr python调用prin()t时,自动调用__str__和__repr__, python调用str()时,自动调用__str__和__repr__, python调用repr()时,自动调用_…...

卷积神经网络(AlexNet)鸟类识别
文章目录 一、前言二、前期工作1. 设置GPU(如果使用的是CPU可以忽略这步)2. 导入数据3. 查看数据 二、数据预处理1. 加载数据2. 可视化数据3. 再次检查数据4. 配置数据集 三、AlexNet (8层)介绍四、构建AlexNet (8层)网络模型五、…...
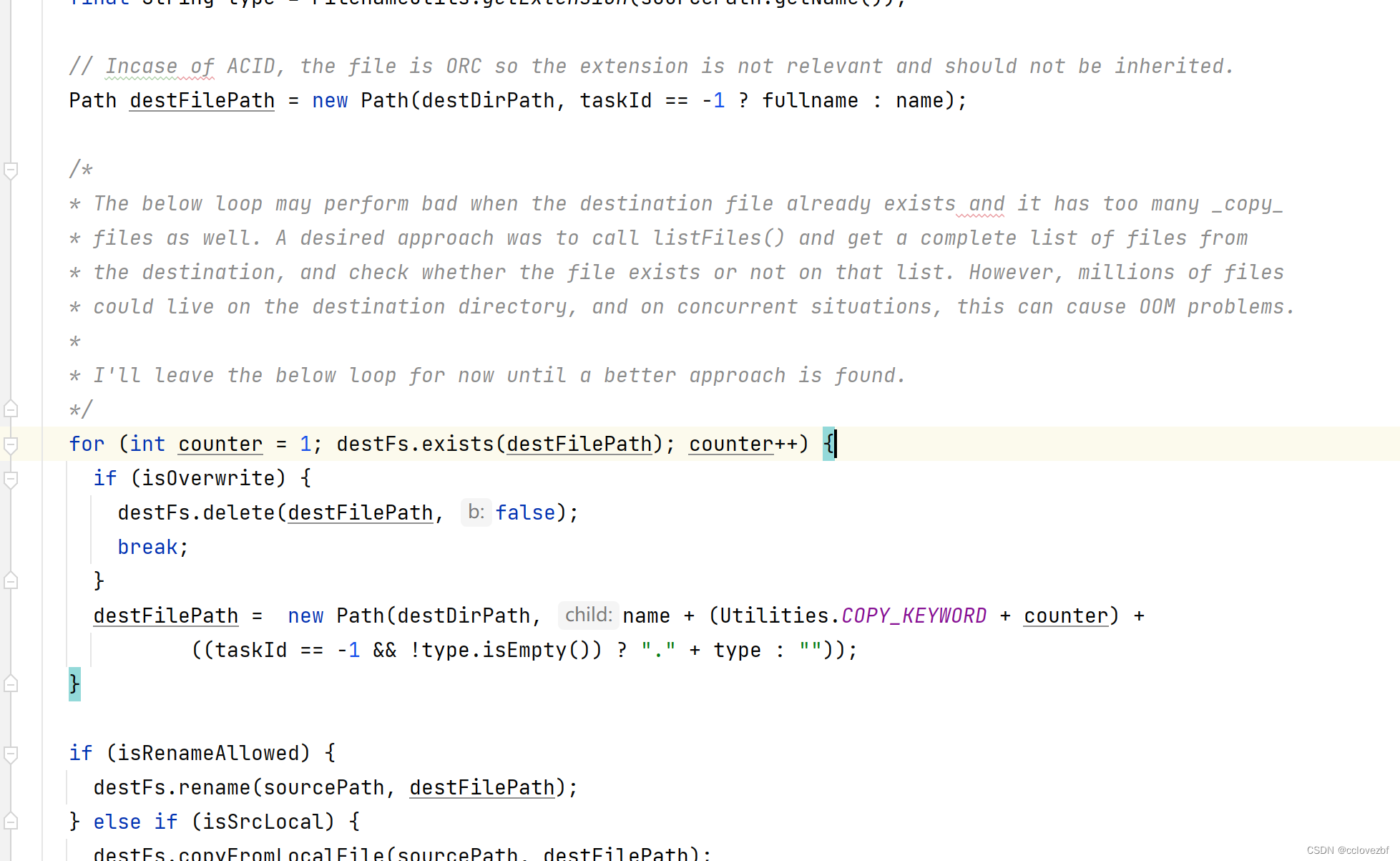
hive 报错return code 40000 from org.apache.hadoop.hive.ql.exec.MoveTask解决思路
参考学习 https://github.com/apache/hive/blob/2b57dd27ad61e552f93817ac69313066af6562d9/ql/src/java/org/apache/hadoop/hive/ql/ErrorMsg.java#L47 为啥学习error code 开发过程中遇到以下错误,大家觉得应该怎么办?从哪方面入手呢? 1.百…...

XML Group端口详解
在XML数据映射过程中,经常需要对数据进行分组聚合操作。例如,当处理包含多个物料明细的XML文件时,可能需要将相同物料号的明细归为一组,或对相同物料号的数量进行求和计算。传统实现方式通常需要编写脚本代码,增加了开…...

相机Camera日志实例分析之二:相机Camx【专业模式开启直方图拍照】单帧流程日志详解
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了: 这一篇我们开始讲: 目录 一、场景操作步骤 二、日志基础关键字分级如下 三、场景日志如下: 一、场景操作步骤 操作步…...

UDP(Echoserver)
网络命令 Ping 命令 检测网络是否连通 使用方法: ping -c 次数 网址ping -c 3 www.baidu.comnetstat 命令 netstat 是一个用来查看网络状态的重要工具. 语法:netstat [选项] 功能:查看网络状态 常用选项: n 拒绝显示别名&#…...

数据链路层的主要功能是什么
数据链路层(OSI模型第2层)的核心功能是在相邻网络节点(如交换机、主机)间提供可靠的数据帧传输服务,主要职责包括: 🔑 核心功能详解: 帧封装与解封装 封装: 将网络层下发…...

相机从app启动流程
一、流程框架图 二、具体流程分析 1、得到cameralist和对应的静态信息 目录如下: 重点代码分析: 启动相机前,先要通过getCameraIdList获取camera的个数以及id,然后可以通过getCameraCharacteristics获取对应id camera的capabilities(静态信息)进行一些openCamera前的…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一)
宇树机器人多姿态起立控制强化学习框架论文解析 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一) 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化…...

04-初识css
一、css样式引入 1.1.内部样式 <div style"width: 100px;"></div>1.2.外部样式 1.2.1.外部样式1 <style>.aa {width: 100px;} </style> <div class"aa"></div>1.2.2.外部样式2 <!-- rel内表面引入的是style样…...

vulnyx Blogger writeup
信息收集 arp-scan nmap 获取userFlag 上web看看 一个默认的页面,gobuster扫一下目录 可以看到扫出的目录中得到了一个有价值的目录/wordpress,说明目标所使用的cms是wordpress,访问http://192.168.43.213/wordpress/然后查看源码能看到 这…...

Razor编程中@Html的方法使用大全
文章目录 1. 基础HTML辅助方法1.1 Html.ActionLink()1.2 Html.RouteLink()1.3 Html.Display() / Html.DisplayFor()1.4 Html.Editor() / Html.EditorFor()1.5 Html.Label() / Html.LabelFor()1.6 Html.TextBox() / Html.TextBoxFor() 2. 表单相关辅助方法2.1 Html.BeginForm() …...
HybridVLA——让单一LLM同时具备扩散和自回归动作预测能力:训练时既扩散也回归,但推理时则扩散
前言 如上一篇文章《dexcap升级版之DexWild》中的前言部分所说,在叠衣服的过程中,我会带着团队对比各种模型、方法、策略,毕竟针对各个场景始终寻找更优的解决方案,是我个人和我司「七月在线」的职责之一 且个人认为,…...
