UVA1025 城市里的间谍 A Spy in the Metro
UVA1025 城市里的间谍 A Spy in the Metro
题面翻译
题目大意
某城市地铁是一条直线,有 n n n( 2 ≤ n ≤ 50 2\leq n\leq 50 2≤n≤50)个车站,从左到右编号 1 … n 1\ldots n 1…n。有 M 1 M_1 M1 辆列车从第 1 1 1 站开始往右开,还有 M 2 M_2 M2 辆列车从第 n n n 站开始往左开。列车在相邻站台间所需的运行时间是固定的,因为所有列车的运行速度是相同的。在时刻 0 0 0,Mario 从第 1 1 1 站出发,目的在时刻 T T T( 0 ≤ T ≤ 200 0\leq T\leq 200 0≤T≤200)会见车站 n n n 的一个间谍。在车站等车时容易被抓,所以她决定尽量躲在开动的火车上,让在车站等待的时间尽量短。列车靠站停车时间忽略不计,且 Mario 身手敏捷,即使两辆方向不同的列车在同一时间靠站,Mario 也能完成换乘。
输入格式
输入文件包含多组数据。
每一组数据包含以下 7 7 7 行:
第一行是一个正整数 n n n,表示有 n n n 个车站。
第二行是为 T T T,表示 Mario 在时刻 T T T 会见车站 n n n 的间谍。
第三行有 n − 1 n-1 n−1 个整数 t 1 , t 2 , … , t n − 1 t_1,t_2,\ldots,t_{n-1} t1,t2,…,tn−1,其中 t i t_i ti 表示地铁从车站 i i i 到 i + 1 i+1 i+1 的行驶时间。
第四行为 M 1 M_1 M1,及从第一站出发向右开的列车数目。
第五行包含 M 1 M_1 M1 个正整数 a 1 , a 2 , … , a M 1 a_1,a_2,\ldots,a_{M_1} a1,a2,…,aM1,即每个列车出发的时间。
第六行为 M 2 M_2 M2 ,即从第 n n n 站出发向左开的列车数目。
第七行包含 M 2 M_2 M2 个正整数 b 1 , b 2 , … , b M 2 b_1,b_2,\ldots,b_{M_2} b1,b2,…,bM2,即每个列车出发的时间。
输入文件以一行 0 0 0 结尾。
输出格式
有若干行,每行先输出 Case Number XXX : (XXX为情况编号,从 1 1 1 开始),再输出最少等待时间或 impossible(无解)。
题目描述
输入格式
输出格式
样例 #1
样例输入 #1
4
55
5 10 15
4
0 5 10 20
4
0 5 10 15
4
18
1 2 3
5
0 3 6 10 12
6
0 3 5 7 12 15
2
30
20
1
20
7
1 3 5 7 11 13 17
0
样例输出 #1
Case Number 1: 5
Case Number 2: 0
Case Number 3: impossible
Solution
采用动态规划算法
设dp[i][j]代表第i时刻到在第j站的等待的时间,因为要在T时间内达到第n站,且要求尽可能多的时间在地铁上度过,由此可以知要求dp[T][n]=0,通过逆向递推建立状态转移方程,可以得到以下三种情况
dp[i][j]=dp[i+1][j]+1,即dp[i][j]为在i+1时刻在第j站的所等待的时间+1dp[i][j]=min(dp[i+t[j]][j+1],dp[i][j]),即若第i时刻存在向右开的车,且此时到达下一个站的时间不大于T时,dp[i][j]为第i+t[j]时刻在第j+1站台所等待的时间与在在这个站台等待的时间点最小值dp[i][j]=min(dp[i+t[j-1]][j-1],dp[i][j]),即若第i时刻存在向左开的车,且此时到达下一个站的时间不大于T时,dp[i][j]为第i+t[j-1]时刻在第j-1站台所等待的时间与在在这个站台等待的时间点最小值
然后最终等待时间为dp[0][1],即在0时刻在1站台时等待的时间
//
// Created by Gowi on 2023/11/23.
//#include <iostream>
#include <cstring>#define maxN 100
#define MaxT 300
#define INF 1000000000using namespace std;int T, t[maxN], a[maxN], b[maxN], M1, M2, n;
int has_train[MaxT][maxN][2];// has_train[i][j][1/2] i时刻在第j个站是否有向右(0)/左(1)开的火车
int dp[MaxT][maxN]; //dp[i][j]i时刻在第j个站需要等待多长时间bool init() {int d;cin >> n;if (n == 0) {return false;}memset(t, 0, sizeof(t));memset(a, 0, sizeof(a));memset(b, 0, sizeof(b));memset(has_train, 0, sizeof(has_train));memset(dp, 0, sizeof(dp));cin >> T;for (int i = 1; i < n; ++i) {cin >> t[i];}cin >> M1;for (int i = 1; i <= M1; ++i) {cin >> a[i];d = a[i];for (int j = 1; j < n; ++j) {has_train[d][j][0] = 1;d += t[j];}}cin >> M2;for (int i = 1; i <= M2; ++i) {cin >> b[i];d = b[i];for (int j = n - 1; j > 0; j--) {has_train[d][j+1][1] = 1;d += t[j];}}return true;
}int main() {int k = 0;while (init()) {for (int i = 1; i < n; ++i) {dp[T][i] = INF;}dp[T][n] = 0;for (int i = T - 1; i >= 0; i--) {for (int j = 1; j <= n; ++j) {dp[i][j] = dp[i + 1][j] + 1; // 等待一分钟if (j < n && has_train[i][j][0] && i + t[j] <= T) { //若此时向右有车,且到达下一个站的时间不大于Tdp[i][j] = min(dp[i][j], dp[i + t[j]][j + 1]); //状态转移方程}if (j > 1 && has_train[i][j][1] && i + t[j-1] <= T) { //若此时向左有车,且到达下一个站的时间不大于Tdp[i][j] = min(dp[i][j], dp[i + t[j - 1]][j - 1]); //状态转移方程}}}cout << "Case Number " << ++k << ": ";if (dp[0][1] >= INF) {cout << "impossible" << endl;} else {cout << dp[0][1] << endl;}}return 0;
}
相关文章:

UVA1025 城市里的间谍 A Spy in the Metro
UVA1025 城市里的间谍 A Spy in the Metro 题面翻译 题目大意 某城市地铁是一条直线,有 n n n( 2 ≤ n ≤ 50 2\leq n\leq 50 2≤n≤50)个车站,从左到右编号 1 … n 1\ldots n 1…n。有 M 1 M_1 M1 辆列车从第 1 1 1 站开…...

【科普知识】什么是步进电机?
德国百格拉公司于1973年发明了五相混合式步进电机及其驱动器,1993年又推出了性能更加优越的三相混合式步进电机。我国在80年代以前,一直是反应式步进电机占统治地位,混合式步进电机是80年代后期才开始发展。 步进电机是一种用电脉冲信号进行…...
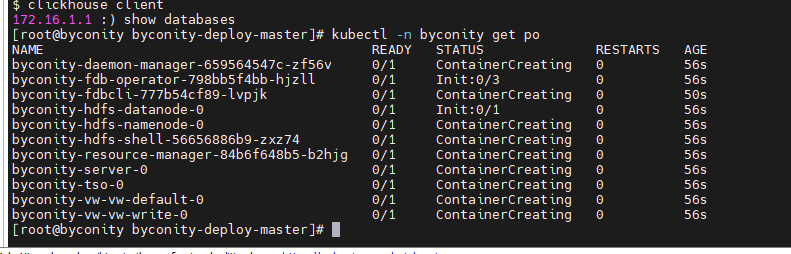
AWS云服务器EC2实例实现ByConity快速部署
1. 前言 亚马逊是全球最大的在线零售商和云计算服务提供商。AWS云服务器在全球范围内都备受推崇,被众多业内人士誉为“云计算服务的行业标准”。在国内,亚马逊AWS也以其卓越的性能和服务满足了众多用户的需求,拥有着较高的市场份额和竞争力。…...

Docker的项目资源参考
Docker的项目资源包括以下内容: Docker官方网站:https://www.docker.com/ Docker Hub:https://hub.docker.com/ Docker文档:https://docs.docker.com/ Docker GitHub仓库:https://github.com/docker Docker官方博客…...

wsl-ubuntu 系统端口总被主机端口占用问题解决
wsl-ubuntu 系统端口总被主机端口占用问题解决 0. 问题描述1. 解决方法 0. 问题描述 wsl-ubuntu 子系统中的服务,总是启动失败,错误信息是端口被占用。 用一些命令查看,被占用的端口也没有用服务启动。 1. 解决方法 运行, ne…...
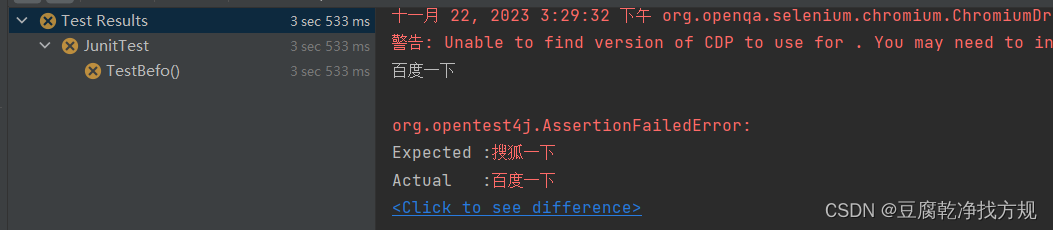
详解自动化之单元测试工具Junit
目录 1.注解 1.1 Test 1.2 BeforeEach 1.3 BeforeAll 1.4 AfterEach 1.5 AfterAll 2. 用例的执行顺序 通过 order() 注解来排序 3. 参数化 3.1 单参数 3.2 多参数 3.3 多参数(从第三方csv文件读取数据源) 3.4 动态参数ParameterizedTest MethodSource() 4. 测试…...

超声波雪深传感器冬季里的科技魔法
在冬季的某个清晨,当你打开大门,被厚厚的积雪覆盖的大地映入眼帘,你是否曾想过,这片雪地的深度是多少?它又如何影响着我们的生活和环境?今天,我们将为你揭开这个谜团,介绍一款神秘的…...
2023年【熔化焊接与热切割】免费试题及熔化焊接与热切割模拟考试
题库来源:安全生产模拟考试一点通公众号小程序 熔化焊接与热切割免费试题是安全生产模拟考试一点通生成的,熔化焊接与热切割证模拟考试题库是根据熔化焊接与热切割最新版教材汇编出熔化焊接与热切割仿真模拟考试。2023年【熔化焊接与热切割】免费试题及…...

【数据结构】—搜索二叉树(C++实现,超详细!)
🎬慕斯主页:修仙—别有洞天 ♈️今日夜电波:消えてしまいそうです—真夜中 1:15━━━━━━️💟──────── 4:18 🔄 ◀️ ⏸ ▶️…...
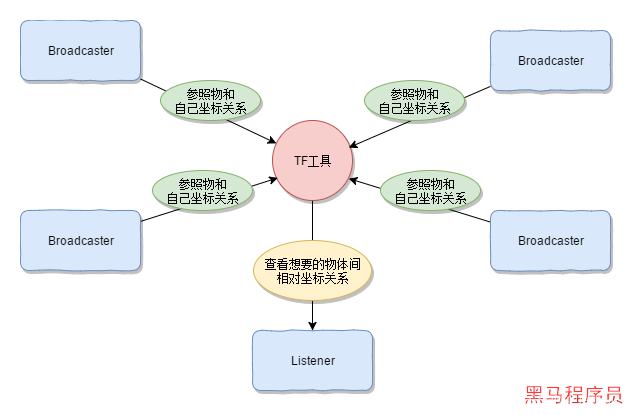
机器人算法—ROS TF坐标变换
1.TF基本概念 (1)什么是TF? TF是Transformations Frames的缩写。在ROS中,是一个工具包,提供了坐标转换等方面的功能。 tf工具包,底层实现采用的是一种树状数据结构,根据时间缓冲并维护多个参考…...
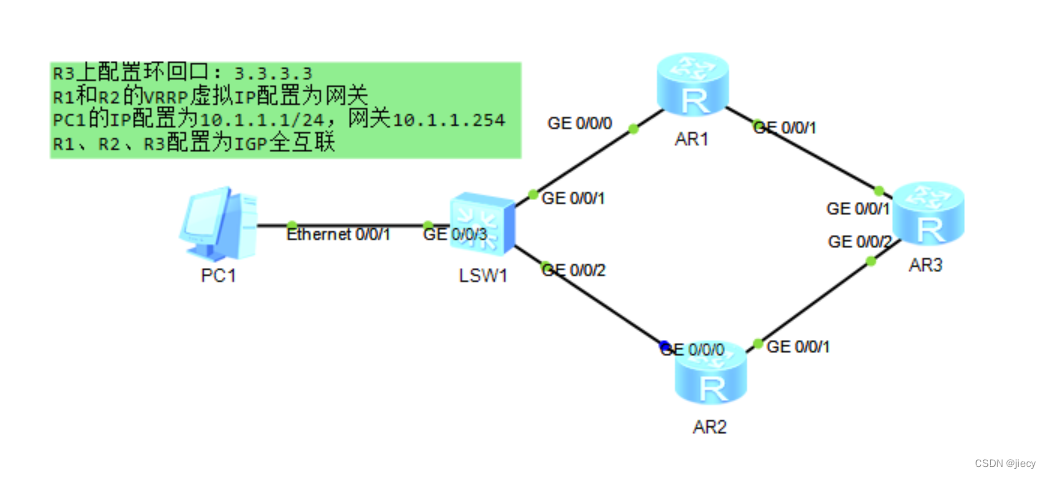
路由VRRP配置例子
拓朴如下: 主要配置如下: [R1] interface GigabitEthernet0/0/0ip address 10.1.1.1 255.255.255.0 vrrp vrid 1 virtual-ip 10.1.1.254vrrp vrid 1 priority 200vrrp vrid 1 preempt-mode timer delay 20 # interface GigabitEthernet0/0/1ip address …...
)
OpenGL 绘制点与三角形(Qt)
文章目录 一、简介二、实现代码三、实现效果一、简介 这里对OpenGL中点与三角形相关绘制操作进行封装,方便后续点云数据与模型数据的渲染。 二、实现代码 这里我们先创建一个基类Drawable,后续的点、线、面等,均会继承该类: Drawable.h #ifndef DRAWABLE_H #define DRAWABL…...

究竟什么是阻塞与非阻塞、同步与异步
文章目录 前言阻塞与非阻塞同步与异步复杂的网络IO真正的异步IOIO分类与示例总结 前言 这几个名词在程序开发时经常听到,但是突然问起来各个词的含义一时间还真是说不清楚,貌似这几个词都是翻译过来的,每个人的解释都不太一样,我…...
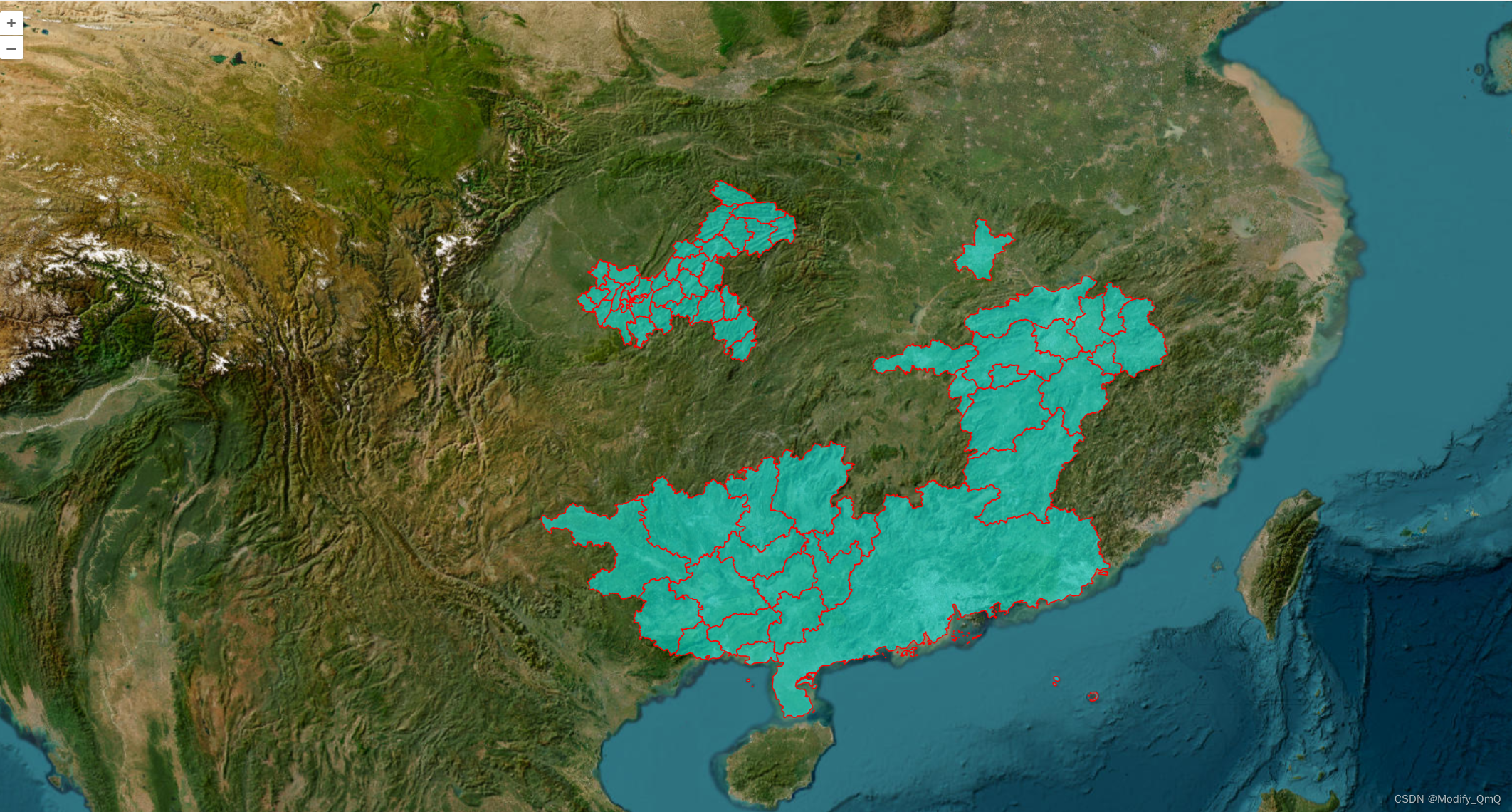
Openlayer【三】—— 绘制多边形GeoJson边界绘制
1.1、绘制多边形 在绘制多边形和前面绘制线有异曲同工之妙,多边形本质上就是由多个点组成的线然后连接组成的面,这个面就是最终的结果,那么这里使用到的是Polygon对象,而传给这个对象的值也是多个坐标,坐标会一个个的…...
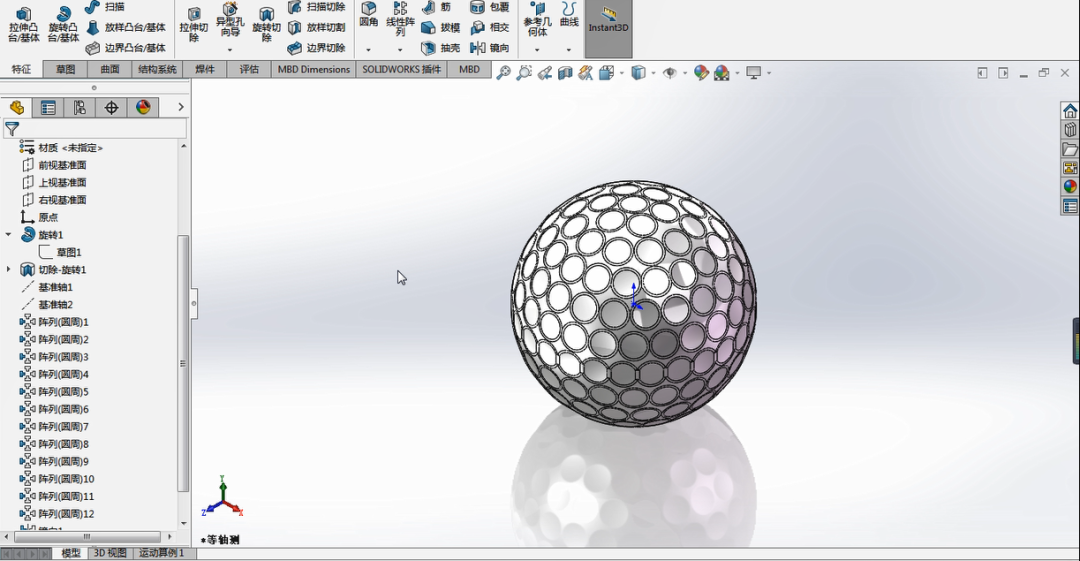
用SOLIDWORKS画个高尔夫球,看似简单的建模却大有学问
SOLIDWORKS软件提供了大量的建模功能,如果工程师能灵活使用这些功能,就可以绘制得到各式各样的模型,我们尝试使用SOLIDWORKS绘制高尔夫球模型,如下图所示。 为什么选用solid works进行建模? solid works是一款功能强大…...

Linux:Network: ARP被动删除的一个情况
今天看到Linux内核里arp代码相关的一个函数,让人想起来很久之前掉进去的一个坑。 说产品的实现里,会存放一个dummy的neighbor(arp记录)在系统里,然后根据这个dummy的记录做一些特殊的处理。 但是当时根本就不知道这个记录的存在,也就无从谈起说要在做设计时考虑它的存在。…...
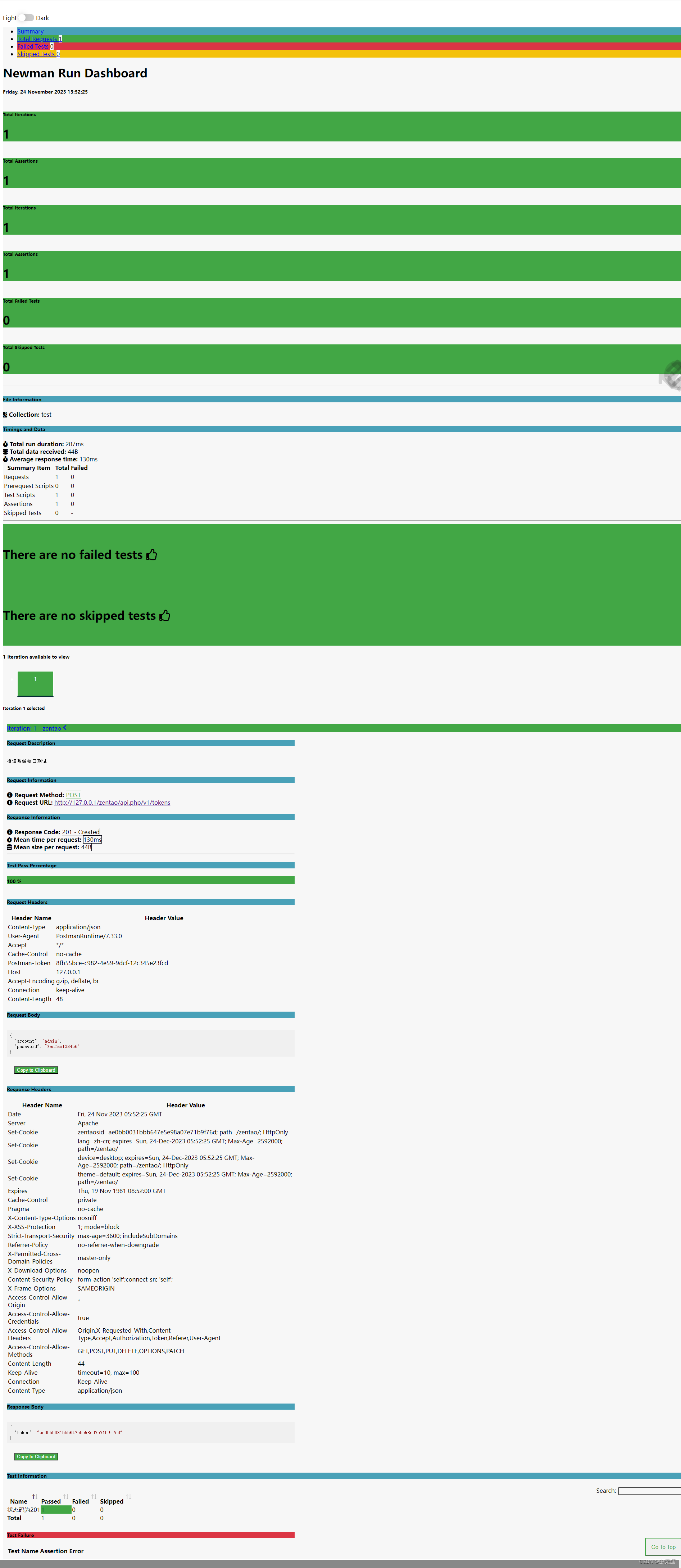
『接口测试干货』| Newman+Postman接口自动化测试完整过程
『接口测试干货』| NewmanPostman接口自动化测试完整过程 1 Newman简介2 如何安装Newman?2.1 安装NodeJs2.2 安装Newman2.2 解决Newman不是内部命令 3 Newman使用3.1 Newman如何运行集合?3.2 如何查看帮助文档?3.3 环境变量设置3.4 关于全局变…...
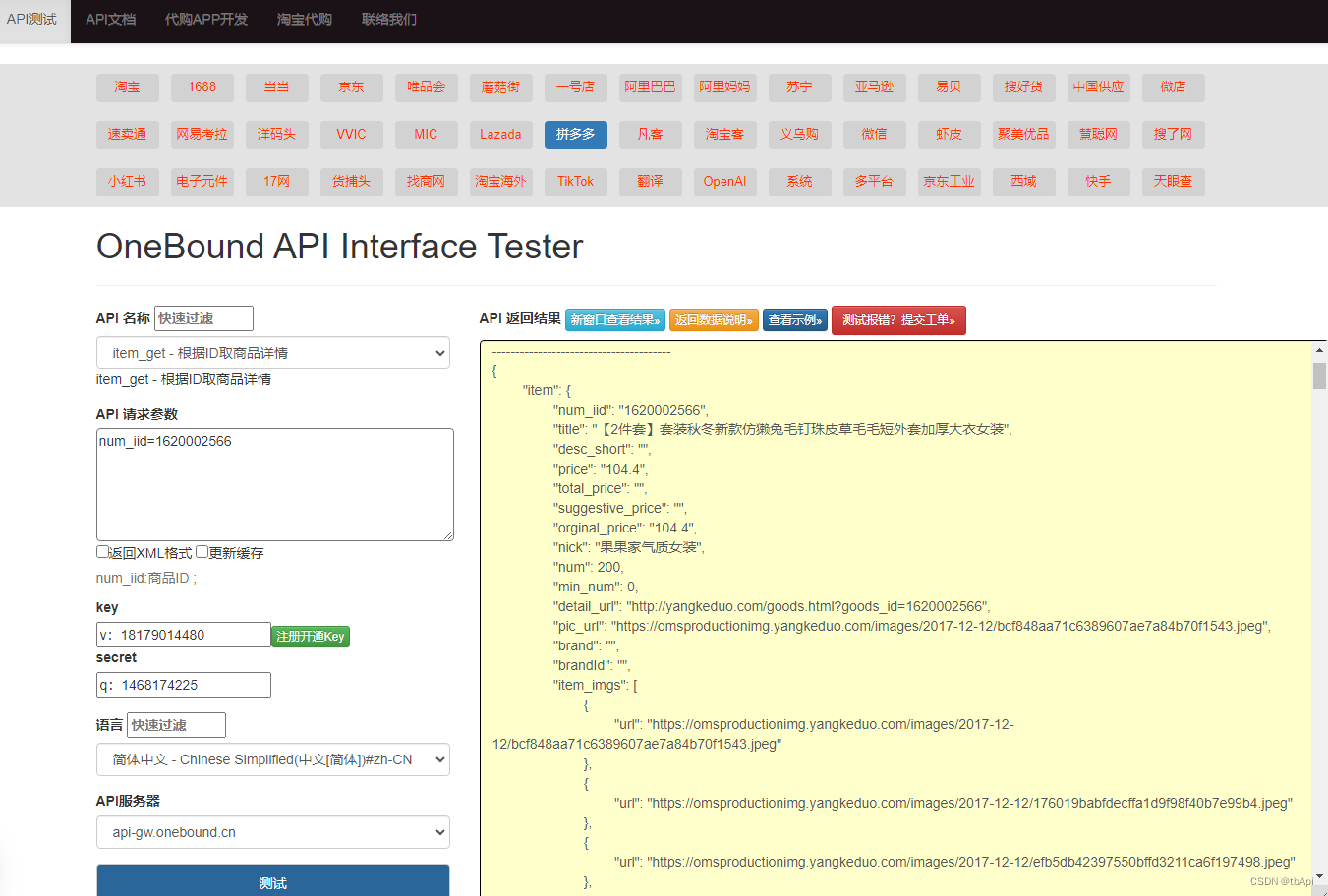
根据商品链接获取拼多多商品详情数据接口|拼多多商品详情价格数据接口|拼多多API接口
拼多多,作为中国最大的社交电商之一,为卖家提供了丰富的商品详情接口。这些接口可以帮助卖家快速获取商品信息,提高销售效率。本文将详细介绍如何使用拼多多商品详情接口,以及它的优势和注意事项。 一、拼多多商品详情接口概述 …...

KaiwuDB 监控组件及辅助 SQL 调优介绍
一、介绍 KaiwuDB 具备完善的行为数据采集功能,此功能要求 KaiwuDB 数据库系统 C/E/T 端不同进程的不同维度的指标采集功能十分完善;在不同进程完成指标采集后,会通过 Opentelemetry 和 Collector 将指标存入 Prometheus,以便查找…...
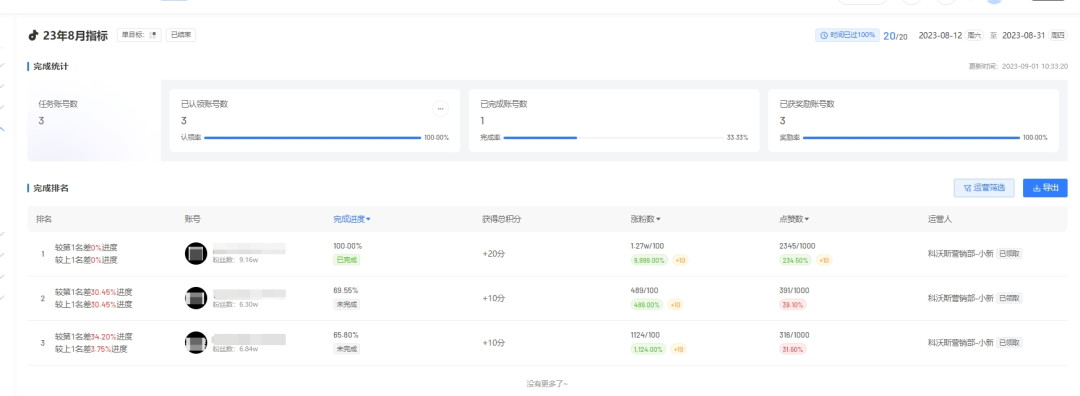
双11再创新高!家电行业如何通过矩阵管理,赋能品牌增长?
双11大促已落下帷幕,虽然今年不再战报满天飞,但从公布的数据来看,家电行业整体表现不俗。 根据抖音电商品牌业务发布的收官战报,家电行业创造了成交新纪录,整体同比增长125%。快手官方数据显示,消电家居行业…...

ES6从入门到精通:前言
ES6简介 ES6(ECMAScript 2015)是JavaScript语言的重大更新,引入了许多新特性,包括语法糖、新数据类型、模块化支持等,显著提升了开发效率和代码可维护性。 核心知识点概览 变量声明 let 和 const 取代 var…...

Zustand 状态管理库:极简而强大的解决方案
Zustand 是一个轻量级、快速和可扩展的状态管理库,特别适合 React 应用。它以简洁的 API 和高效的性能解决了 Redux 等状态管理方案中的繁琐问题。 核心优势对比 基本使用指南 1. 创建 Store // store.js import create from zustandconst useStore create((set)…...

Swift 协议扩展精进之路:解决 CoreData 托管实体子类的类型不匹配问题(下)
概述 在 Swift 开发语言中,各位秃头小码农们可以充分利用语法本身所带来的便利去劈荆斩棘。我们还可以恣意利用泛型、协议关联类型和协议扩展来进一步简化和优化我们复杂的代码需求。 不过,在涉及到多个子类派生于基类进行多态模拟的场景下,…...

(二)TensorRT-LLM | 模型导出(v0.20.0rc3)
0. 概述 上一节 对安装和使用有个基本介绍。根据这个 issue 的描述,后续 TensorRT-LLM 团队可能更专注于更新和维护 pytorch backend。但 tensorrt backend 作为先前一直开发的工作,其中包含了大量可以学习的地方。本文主要看看它导出模型的部分&#x…...

Objective-C常用命名规范总结
【OC】常用命名规范总结 文章目录 【OC】常用命名规范总结1.类名(Class Name)2.协议名(Protocol Name)3.方法名(Method Name)4.属性名(Property Name)5.局部变量/实例变量(Local / Instance Variables&…...

江苏艾立泰跨国资源接力:废料变黄金的绿色供应链革命
在华东塑料包装行业面临限塑令深度调整的背景下,江苏艾立泰以一场跨国资源接力的创新实践,重新定义了绿色供应链的边界。 跨国回收网络:废料变黄金的全球棋局 艾立泰在欧洲、东南亚建立再生塑料回收点,将海外废弃包装箱通过标准…...

第一篇:Agent2Agent (A2A) 协议——协作式人工智能的黎明
AI 领域的快速发展正在催生一个新时代,智能代理(agents)不再是孤立的个体,而是能够像一个数字团队一样协作。然而,当前 AI 生态系统的碎片化阻碍了这一愿景的实现,导致了“AI 巴别塔问题”——不同代理之间…...

Psychopy音频的使用
Psychopy音频的使用 本文主要解决以下问题: 指定音频引擎与设备;播放音频文件 本文所使用的环境: Python3.10 numpy2.2.6 psychopy2025.1.1 psychtoolbox3.0.19.14 一、音频配置 Psychopy文档链接为Sound - for audio playback — Psy…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个生活电费的缴纳和查询小程序
一、项目初始化与配置 1. 创建项目 ohpm init harmony/utility-payment-app 2. 配置权限 // module.json5 {"requestPermissions": [{"name": "ohos.permission.INTERNET"},{"name": "ohos.permission.GET_NETWORK_INFO"…...

【python异步多线程】异步多线程爬虫代码示例
claude生成的python多线程、异步代码示例,模拟20个网页的爬取,每个网页假设要0.5-2秒完成。 代码 Python多线程爬虫教程 核心概念 多线程:允许程序同时执行多个任务,提高IO密集型任务(如网络请求)的效率…...
