python每日一题——4移动0
题目
给定一个数组 nums,编写一个函数将所有 0 移动到数组的末尾,同时保持非零元素的相对顺序。
请注意 ,必须在不复制数组的情况下原地对数组进行操作。
示例 1:
输入: nums = [0,1,0,3,12]
输出: [1,3,12,0,0]
示例 2:
输入: nums = [0]
输出: [0]
答案
这道题可以使用双指针的方法解决,一个指针用来遍历数组,一个指针用来记录0的末尾位置。
具体步骤如下:
定义两个指针,一个指向当前遍历的位置,一个指向0的末尾位置。
遍历数组,如果当前元素为0,则将其移动到0的末尾位置,并将0的末尾位置指针向前移动一位。
如果当前元素不为0,则将其移动到当前位置,并将当前位置指针向前移动一位。
重复上述步骤,直到遍历完整个数组。
代码如下:
def moveZeroes(nums): if not nums: return [] left = 0 # 当前遍历位置指针 right = 0 # 0的末尾位置指针 n = len(nums) while left < n: if nums[left] == 0: nums[left], nums[right] = nums[right], nums[left] right += 1 else: nums[left] = nums[left] + 1 # 非零元素加上一个非零值,保证相对顺序不变 left += 1 return nums
时间复杂度为O(n),空间复杂度为O(1)。
相关文章:

python每日一题——4移动0
题目 给定一个数组 nums,编写一个函数将所有 0 移动到数组的末尾,同时保持非零元素的相对顺序。 请注意 ,必须在不复制数组的情况下原地对数组进行操作。 示例 1: 输入: nums [0,1,0,3,12] 输出: [1,3,12,0,0] 示例 2: 输入: nums [0]…...
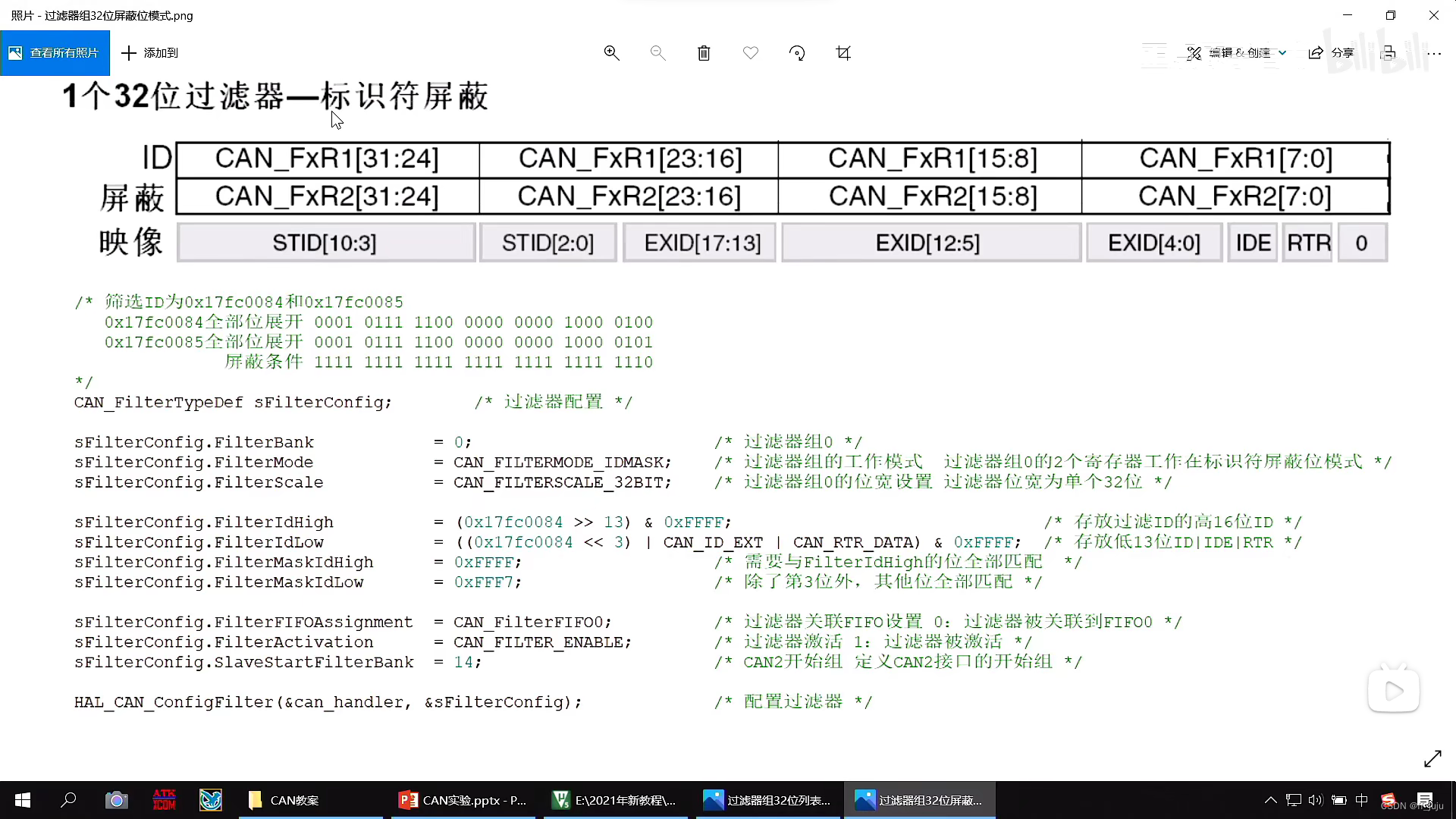
CAN实验
CAN 寄存器 HAL库函数 代码 #include "./BSP/CAN/can.h"CAN_HandleTypeDef g_can1_handle; CAN_TxHeaderTypeDef g_can1_txheader; CAN_RxHeaderTypeDef g_can1_rxheader;/* STM32F103 TS1 8 TS2 7 BRP 3 波特率:36000 / [(9 8 1) * 4] 500Kbps …...
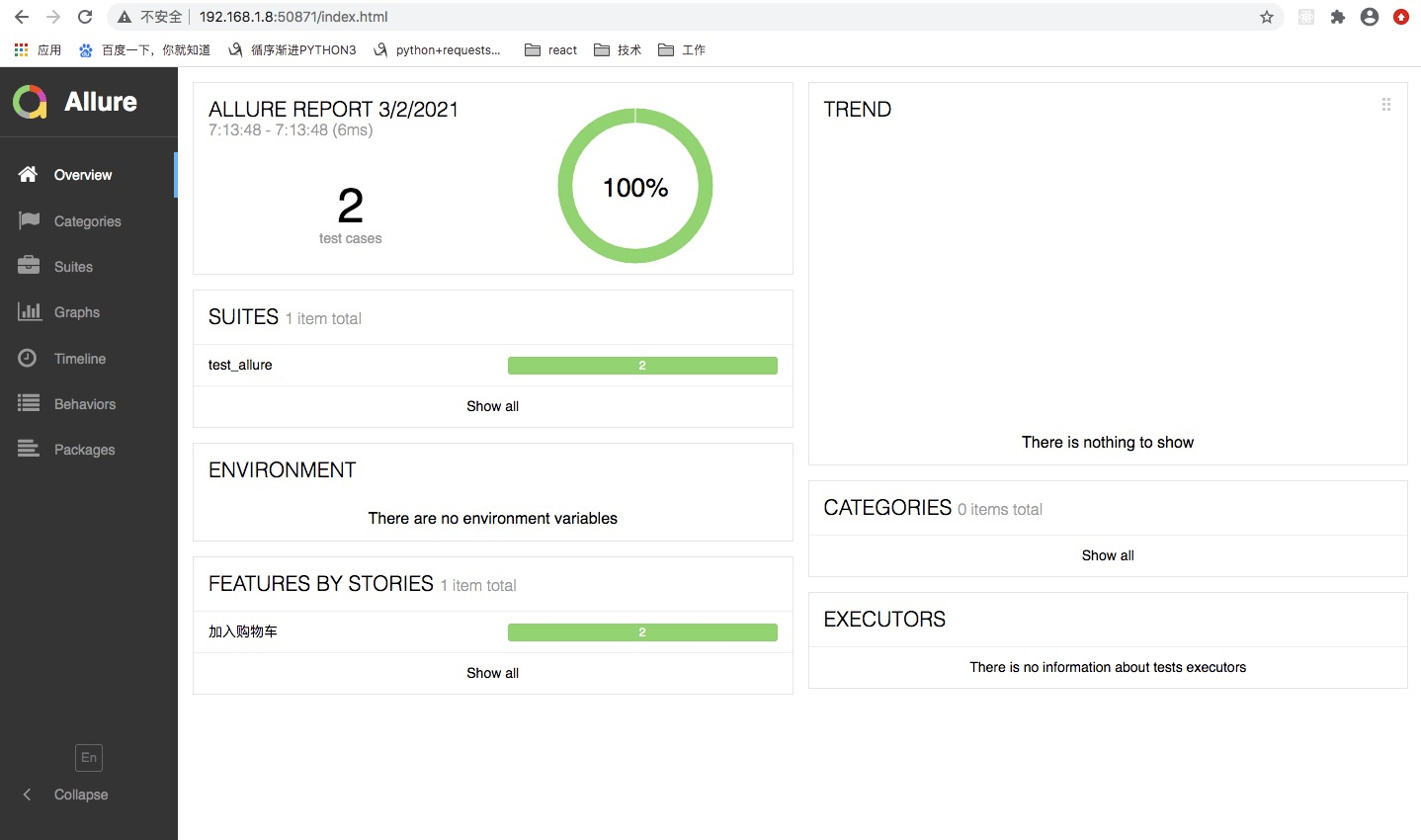
(一)pytest自动化测试框架之生成测试报告(mac系统)
前言 我们可以通过pytest-html插件来生成测试报告,但是pytest-html插件生成的测试报告不够美观,逼格也不够高,通过allure生成的测试报告是比较美观的,花里胡哨的,能够提升一个level。 allure官网: Allure…...

微服务实战系列之Nginx
前言 Nginx?写了那么多文章,为什么今天才轮到它的表演?那是因为它实在太重要了,值得大书特书,特别对待。 当我们遇到单点瓶颈,第一个idea是?Nginx; 当我们需要反向代理,…...

使用rsync从OpenShift的pod复制文件
环境 Red Hat Enterprise Linux release 8.6 (Ootpa)OCP 4.12.22 准备 安装rsync: yum install rsync 查看pod: [rootapi.kai1123.cp.fyre.ibm.com ~]# oc get pod -n cpd-instance | grep dmc ...... ibm-dmc-1700727413211000-monitor-0 …...
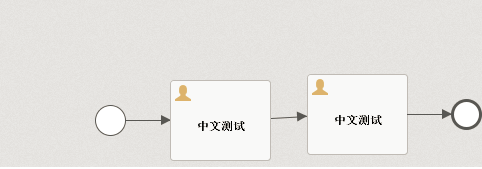
解决Activiti5.22流程图部署在Windows上正常,但在linux上部署后出现中文变方块的问题
总结/朱季谦 楼主最近在做公司的工作流平台,发现一个很无语的事情,Activiti5.22的流程图在Windows环境上部署,是可以正常查看的,但发布到公司的Linux服务器上后,在上面进行流程图在线部署时,发现中文都变成…...
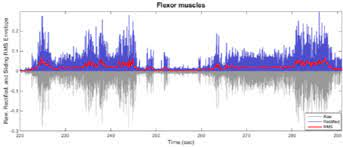
EMG肌肉电信号处理合集(三)
本文主要展示常见的肌电信号预处理的实现,开发环境为matlab。 目录 1 肌电信号低通,高通,带通滤波 2 去除DC 0阶偏置,1阶偏置 3 全波整流 4 信号降采样 5 linear envolope / butterworth 低通滤波器 1 肌电信号低通…...
GitHub桌面版
GitHub桌面版 一、GitHub 桌面版二、clone 仓库三、更新仓库 一、GitHub 桌面版 二、clone 仓库 三、更新仓库...
【广州华锐互动】昆虫3D虚拟动态展示:探索神奇的微观世界
在这个充满科技魅力的时代,我们可以通过各种方式去了解和探索自然界的奥秘。而昆虫作为地球上最为丰富多样的生物群体之一,其独特的生活习性和形态特征一直吸引着人们的目光。 由广州华锐互动开发的昆虫3D虚拟动态展示系统,成为了一种全新的科…...

《QT从基础到进阶·三十六》QWidget实现收缩栏的效果
功能: 1、可以在收缩栏插件中添加界面 2、可以把界面展开或收缩 3、可以用鼠标拖动界面改变界面的排放顺序 源码放在最下方 1、可以在收缩栏插件中添加界面 virtual void addWidget(QWidget* widget, const QString& label, const QIcon& icon QIcon())…...
运行软件报错找不到vcruntime140.dll无法继续执行代码怎么办-6个解决方法
vcruntime140.dll是一个由Microsoft Visual C提供的运行时库文件,它为许多Microsoft Visual Studio开发的应用程序提供了必要的支持。这个文件对于许多Windows应用程序的正常运行至关重要。然而,有时会出现vcruntime140.dll缺失的问题,导致应…...
从Discord的做法中学习 — 使用Golang进行请求合并
正如你可能之前看到的,Discord去年发布了一篇有价值的文章,讨论了他们成功存储了数万亿条消息。虽然有很多关于这篇文章的YouTube视频和文章,但我认为这篇文章中一个名为“数据服务为数据服务”的部分没有得到足够的关注。在这篇文章中&#…...

【教3妹学编程-算法题】统计和小于目标的下标对数目
2哥 : 3妹,OpenAI的宫斗剧迎来了大结局!OpenAI宣布阿尔特曼复职CEO,董事会重组 3妹:啊?到底谁才是幕后操纵者啊,有咩有揪出来 2哥 : 也不是很清楚,据说在被开除的几周前,前CEO曾谴责…...
OSG粒子系统与阴影-雾效模拟(1)
虚拟现实中有很多效果,如雨效、雪效、雾效等,这些都可以通过粒子系统来实现。一个真实的粒子系统的模式能使三维场景达到更好的效果。 本章对OSG粒子系统的使用以及生成自定义粒子系统的方法进行了详细介绍最后还附带说明了阴影的使用方法。在实时的场景…...
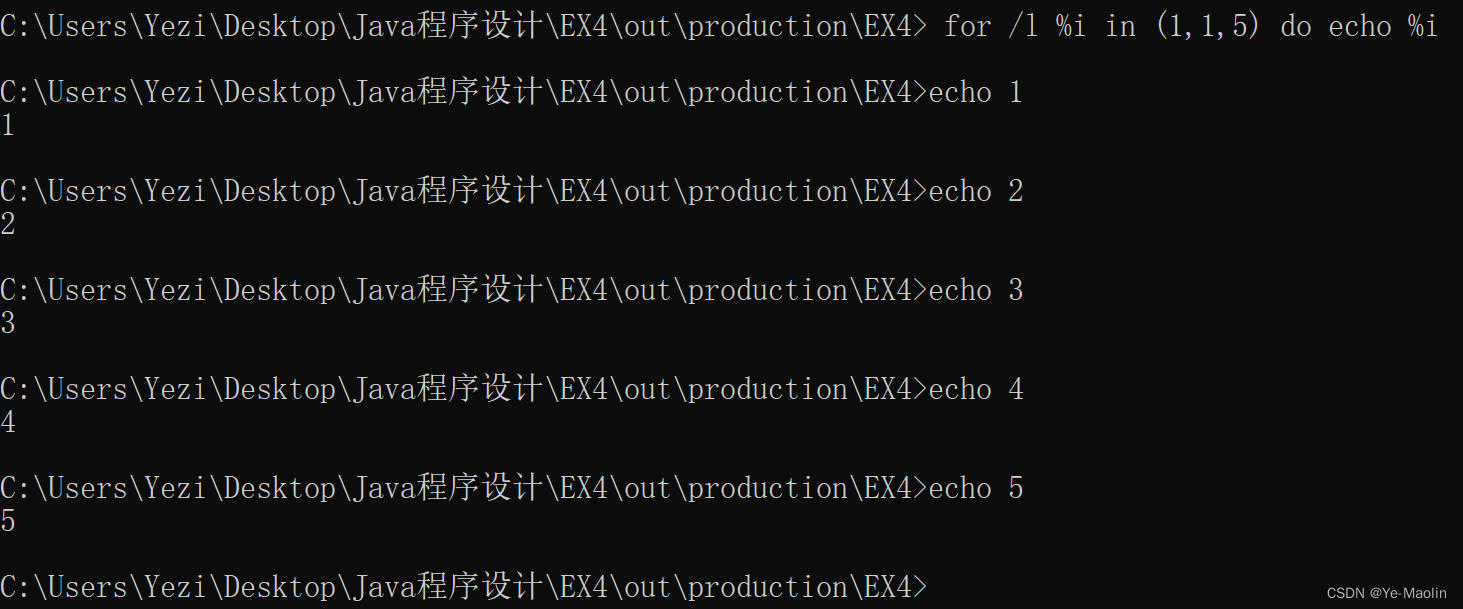
Windows power shell for循环
有时候需要重复执行某个shell命令 for($i1;$i -lt 10;$i$i1){echo $i}如果是cmd for /l %i in (1,1,5) do echo %i...

GIT实践与常用命令---回退
实践场景 场景1 回退提交 在日常工作中,我们可能会和多个同事在同一个分支进行开发,有时候我们可能会出现一些错误提交,这些错误提交如果想撤销,可以有两种解决办法:回退( reset )、反做(revert) keywords:reset、rev…...

Python-Django的“日志功能-日志模块(logging模块)-日志输出”的功能详解
01-综述 可以使用Python内置的logging模块来实现Django项目的日志记录。 所以与其说这篇文章在讲Django的“日志功能-日志模块-日志输出”,不如说是在讲Pthon的“日志功能-日志模块-日志输出”,即Python的logging模块。 下面用一个实例来进行讲解。 …...
笔记——库对数值和字符数据的支持)
C现代方法(第23章)笔记——库对数值和字符数据的支持
文章目录 第23章 库对数值和字符数据的支持23.1 <float.h>: 浮点类型的特性23.2 <limits.h>: 整数类型的大小23.3 <math.h>: 数学计算(C89)23.3.1 错误23.3.2 三角函数23.3.3 双曲函数23.3.4 指数函数和对数函数23.3.5 幂函数23.3.6 就近舍入、绝对值函数和取…...
NSGA-II求解微电网多目标优化调度(MATLAB)
一、NSGA-II简介 NSGA-Ⅱ算法是Kalyanmoy Deb等人于 2002年在 NSGA 的基础上提出的,它比 NSGA算法更加优越:它采用了快速非支配排序算法,计算复杂度比 NSGA 大大的降低;采用了拥挤度和拥挤度比较算子,代替了需要指定的…...

7-9 jmu-python-班级人员信息统计
7-9 jmu-python-班级人员信息统计 分数 15 作者 郑如滨 单位 集美大学 输入a,b班的名单,并进行如下统计。 输入格式: 第1行::a班名单,一串字符串,每个字符代表一个学生,无空格,可能有重复字符。 第2行:&am…...

华为云AI开发平台ModelArts
华为云ModelArts:重塑AI开发流程的“智能引擎”与“创新加速器”! 在人工智能浪潮席卷全球的2025年,企业拥抱AI的意愿空前高涨,但技术门槛高、流程复杂、资源投入巨大的现实,却让许多创新构想止步于实验室。数据科学家…...

docker详细操作--未完待续
docker介绍 docker官网: Docker:加速容器应用程序开发 harbor官网:Harbor - Harbor 中文 使用docker加速器: Docker镜像极速下载服务 - 毫秒镜像 是什么 Docker 是一种开源的容器化平台,用于将应用程序及其依赖项(如库、运行时环…...

线程与协程
1. 线程与协程 1.1. “函数调用级别”的切换、上下文切换 1. 函数调用级别的切换 “函数调用级别的切换”是指:像函数调用/返回一样轻量地完成任务切换。 举例说明: 当你在程序中写一个函数调用: funcA() 然后 funcA 执行完后返回&…...

MMaDA: Multimodal Large Diffusion Language Models
CODE : https://github.com/Gen-Verse/MMaDA Abstract 我们介绍了一种新型的多模态扩散基础模型MMaDA,它被设计用于在文本推理、多模态理解和文本到图像生成等不同领域实现卓越的性能。该方法的特点是三个关键创新:(i) MMaDA采用统一的扩散架构…...

现代密码学 | 椭圆曲线密码学—附py代码
Elliptic Curve Cryptography 椭圆曲线密码学(ECC)是一种基于有限域上椭圆曲线数学特性的公钥加密技术。其核心原理涉及椭圆曲线的代数性质、离散对数问题以及有限域上的运算。 椭圆曲线密码学是多种数字签名算法的基础,例如椭圆曲线数字签…...

微信小程序云开发平台MySQL的连接方式
注:微信小程序云开发平台指的是腾讯云开发 先给结论:微信小程序云开发平台的MySQL,无法通过获取数据库连接信息的方式进行连接,连接只能通过云开发的SDK连接,具体要参考官方文档: 为什么? 因为…...

Caliper 配置文件解析:config.yaml
Caliper 是一个区块链性能基准测试工具,用于评估不同区块链平台的性能。下面我将详细解释你提供的 fisco-bcos.json 文件结构,并说明它与 config.yaml 文件的关系。 fisco-bcos.json 文件解析 这个文件是针对 FISCO-BCOS 区块链网络的 Caliper 配置文件,主要包含以下几个部…...

C++八股 —— 单例模式
文章目录 1. 基本概念2. 设计要点3. 实现方式4. 详解懒汉模式 1. 基本概念 线程安全(Thread Safety) 线程安全是指在多线程环境下,某个函数、类或代码片段能够被多个线程同时调用时,仍能保证数据的一致性和逻辑的正确性…...
:邮件营销与用户参与度的关键指标优化指南)
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南 在数字化营销时代,邮件列表效度、用户参与度和网站性能等指标往往决定着创业公司的增长成败。今天,我们将深入解析邮件打开率、网站可用性、页面参与时…...

Web 架构之 CDN 加速原理与落地实践
文章目录 一、思维导图二、正文内容(一)CDN 基础概念1. 定义2. 组成部分 (二)CDN 加速原理1. 请求路由2. 内容缓存3. 内容更新 (三)CDN 落地实践1. 选择 CDN 服务商2. 配置 CDN3. 集成到 Web 架构 …...
