概率论与数理统计中常见的随机变量分布律、数学期望、方差及其介绍
1 离散型随机变量
1.1 0-1分布
设随机变量X的所有可能取值为0与1两个值,其分布律为
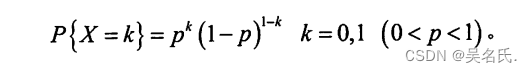
若分布律如上所示,则称X服从以P为参数的(0-1)分布或两点分布。记作X~ B(1,p)
0-1分布的分布律利用表格法表示为:
| X | 0 | 1 |
|---|---|---|
| P | 1-P | P |
0-1分布的数学期望E(X) = 0 * (1 - p) + 1 * p = p
1.2 二项分布
二项分布的分布律如下所示:
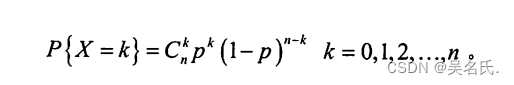
其中P是事件在一次试验中发生的概率,称随机变量X服从参数为n,p 的二项分布,记作X~B(n,p)。当n=1时,X为(0-1)分布
二项分布利用表格法也可表示为:
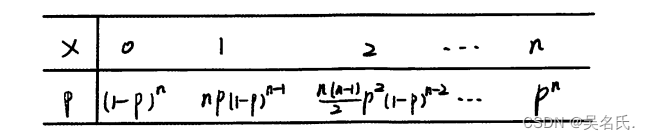
二项分布的数学期望E(X) = np
1.3 泊松分布
设随机变量X所有可能取值是0,12,…,而取各个值的概率为
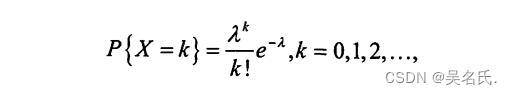
其中λ>0是常数,则称随机变量 X 服从泊松分布,记为 X ~ π(λ)
泊松分布利用表格法可表示为:

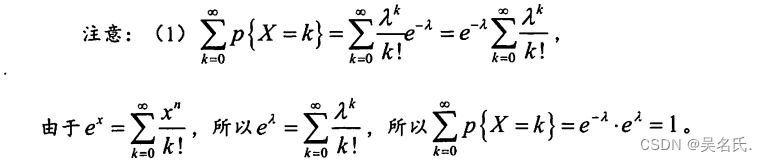
泊松分布的数学期望E(X) = λ
泊松分布的方差D(X) = λ
1.4 几何分布
记X在独立重复试验中事件A首次发生所进行试验的次数,则
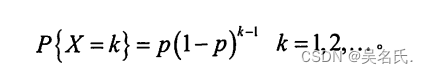
我们称随机变量X服从几何分布,记作X~G§。
几何分布利用表格法也可表示为:

几何分布的数学期望E(X) = 1/p
几何分布的方差D(X) = (1-p)/(p*p)
1.5 超几何分布
设有N件产品,其中有M(MSN)件次品。从中任取n(nN)件产品,用X表示取出的n件产
品中次品的件数,则
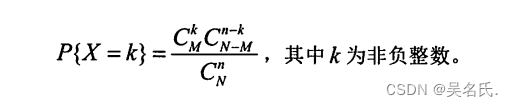
我们称随机变量X服从参数为N、M、n的超几何分布
注意:超几何分布为不放回抽样。
2 连续性随机变量
2.1 均匀分布
2.1.1 均匀分布的密度函数
若连续型随机变量X的概率密度
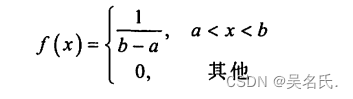
则称f(x)在(a,b)上服从均匀分布,记作X~U(a,b)
2.1.2 均匀分布的分布函数及图像
均匀分布的分布函数为:
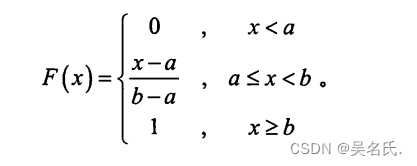
f(x)与F(x)分别如图所示:
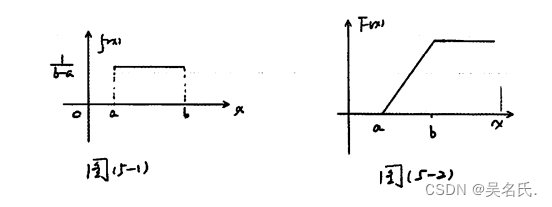
2.1.3 均匀分布的数学期望及其方差
均匀分布的数学期望E(X) = ( a + b ) / 2
均匀分布的方差D(X) = (( b - a ) ^ 2) / 12
2.2 指数分布
2.2.1 指数分布的概率密度
若连续型随机变量X概率密度为:
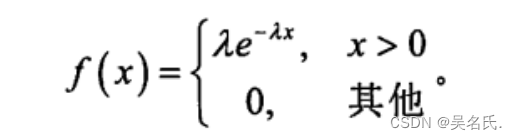
其中λ>0为常数,则称X 服从参数为的指数分布。记作X~ E(λ)
2.2.2 指数分布的分布函数及图像
随机变量X的分布函数和图像为:
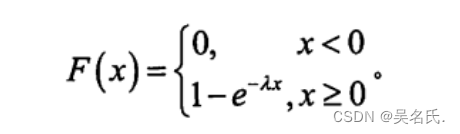
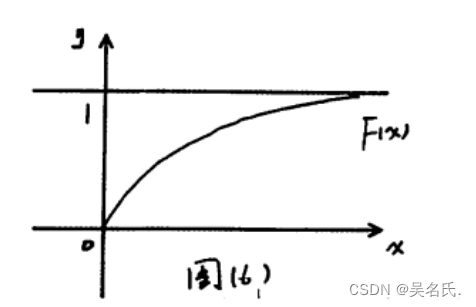
2.2.3 指数分布的数学期望及其方差
指数分布的数学期望E(X) = 1 / λ
指数分布的方差D(X) = 1 / (λ ^ 2)
2.3 正太分布
2.3.1 一般正太分布的密度函数、分布概率及其图像
若连续型随机变量X的概率密度和图像为:
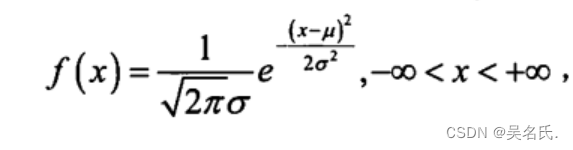
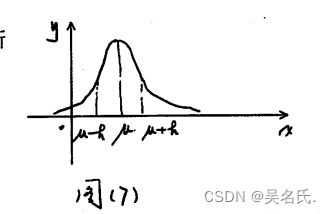
其中μ,σ( σ > 0)为常数,则称服从参数为,的正态分布,记作X~ N(μ, σ * σ),分布函数为:
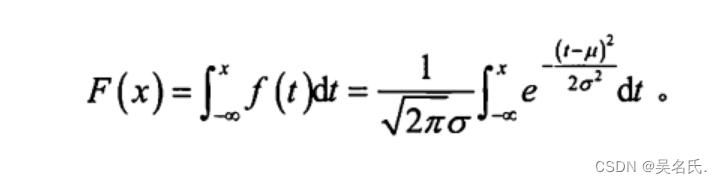
2.3.2 标准正太分布的密度函数、分布概率及其图像
当参数 u=0,σ=1时称随机变量X 服从标准正态分布,记作X~N(0,1)。其概率密度及分布函数如下所示:
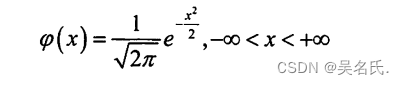
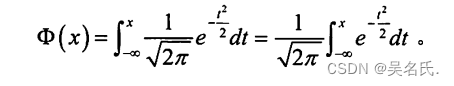
概率密度图像如下所示:
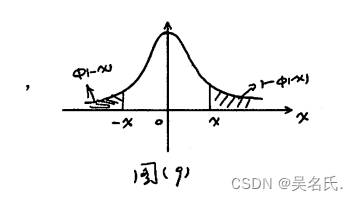
其概率密度函数的图形如图 (9)所示。由(x)的图形,不难得出如下性质:
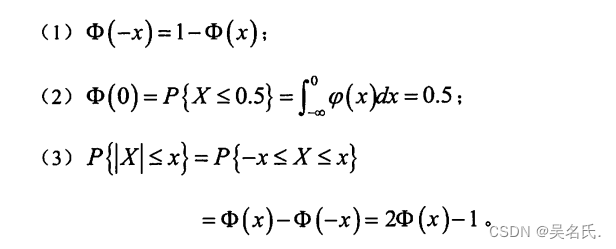
2.3.3 正太分布的数学期望及其方差
正太分布的数学期望E(X) = u
正太分布的方差D(X) = σ
3 数学期望的性质
下面给出数学期望常见的性质:
- 设C是常数,则有E©=C。
- 设X是一个随机变量,C为常数,则有 E(CY)=CE(Y)
- 设X,Y为两个随机变量,则E(XY)=E(Y)E(Y)
- 设X,Y 为相互独立的随机变量,则 E(XY)=E(Y)·E(Y)
数学期望E(X)和方差D(X)之间的关系:
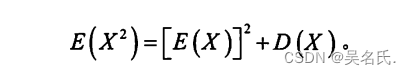
4 方差
4.1 方差的性质
-
设C为常数,则D©=0。
-
@设X是随机变量,C是常数,则有 D(CX)=C^2D(X),D(X+C)=D(X)
-
设XY是两个随机变量,则有
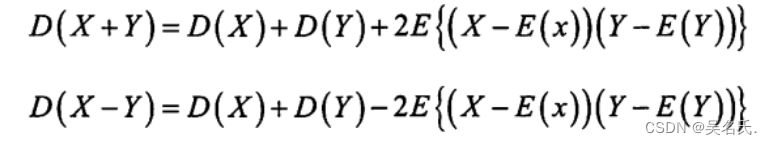 特别地,若X与Y相互独立,则有D(X+Y)=D(X)+D(Y),D(X-Y)=D(X)+D(Y)
特别地,若X与Y相互独立,则有D(X+Y)=D(X)+D(Y),D(X-Y)=D(X)+D(Y) -
D(Y)=0的充分必要条件是以概率为1 取常数 E(X),即P{ X=E(X) } = 1
4.2 协方差和相关系数
协方差公式: cov(X,Y) = E(XY) - EXEY
协方差公式的几个变形:
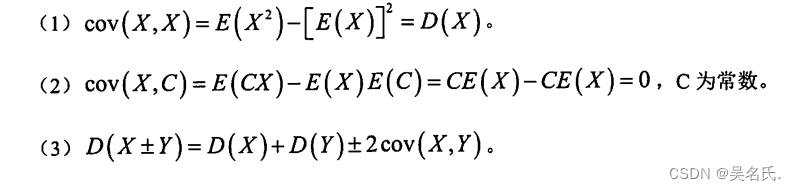
相关系数ρxy公式如下:
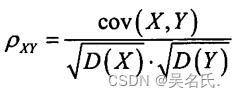
相关文章:
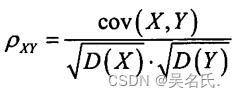
概率论与数理统计中常见的随机变量分布律、数学期望、方差及其介绍
1 离散型随机变量 1.1 0-1分布 设随机变量X的所有可能取值为0与1两个值,其分布律为 若分布律如上所示,则称X服从以P为参数的(0-1)分布或两点分布。记作X~ B(1,p) 0-1分布的分布律利用表格法表示为: X01P1-PP 0-1分布的数学期望E(X) 0 *…...

骨传导耳机的优缺点都有哪些?骨传导耳机值得入手吗?
骨传导耳机的优点还是很多的,相比于传统耳机,骨传导耳机要更值得入手! 下面让我们了解下骨传导耳机的优缺点都有哪些: 一、优点 1、使用更安全 传统的耳机,在使用时会听不到外界的声音,而骨传导耳机通过…...
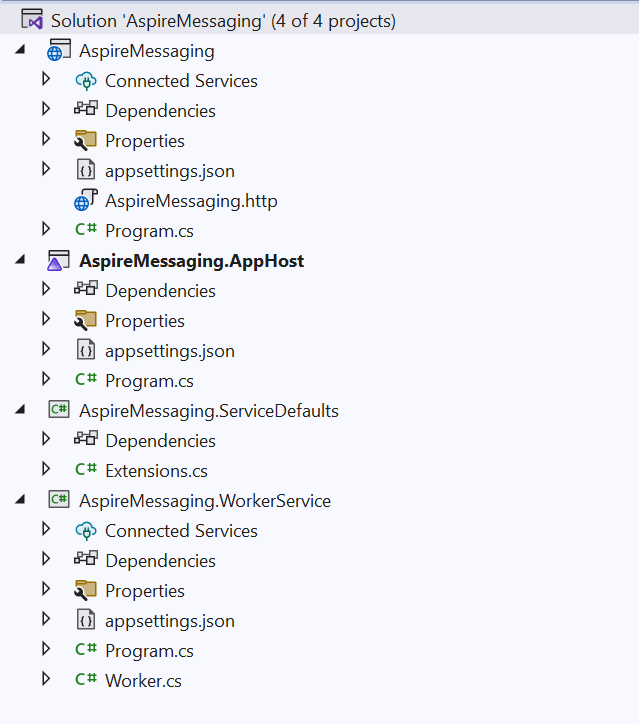
在ASP.NET Core 中使用 .NET Aspire 消息传递组件
前言 云原生应用程序通常需要可扩展的消息传递解决方案,以提供消息队列、主题和订阅等功能。.NET Aspire 组件简化了连接到各种消息传递提供程序(例如 Azure 服务总线)的过程。在本教程中,小编将为大家介绍如何创建一个 ASP.NET …...
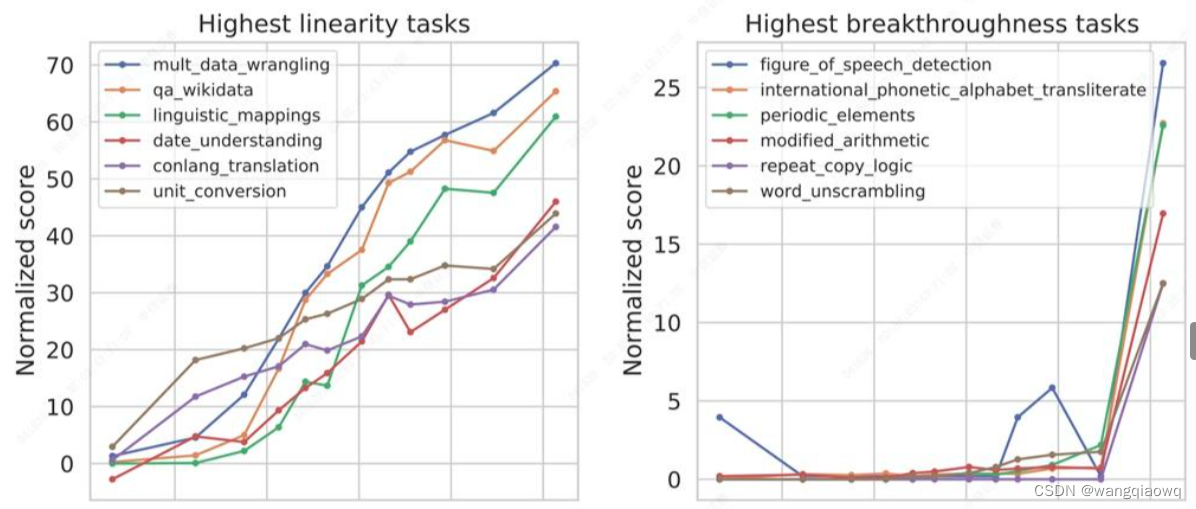
NLP学习
参考:NLP发展之路I - 从词袋模型到Transformer - 知乎 (zhihu.com) NLP大致的发展历史。从最开始的词袋模型,到RNN,到Transformers和BERT,再到ChatGPT,NLP经历了一段不断精进的发展道路。数据驱动和不断完善的端到端的…...

Linux-Ubuntu环境下搭建SVN服务器
Linux-Ubuntu环境下搭建SVN服务器 一、背景二、前置工作2.1确定IP地址保持不变2.2关闭防火墙 三、安装SVN服务器四、修改SVN服务器版本库目录五、调整SVN配置5.1查看需要修改的配置文件5.2修改svnserve.conf文件5.3修改passwd文件,添加账号和密码(window…...
)
python tkinter使用(四)
本篇文章主要讲下tkinter 的文本框相关. tkinter中用Entry来实现输入框,类似于android中的edittext. 具体的用法如下: 1:空白输入框 如下: name tk.Entry(window) name.pack()2: 设置输入框的默认文案 name tk.Entry(window) name.pack() name.insert(tk.END, "请…...
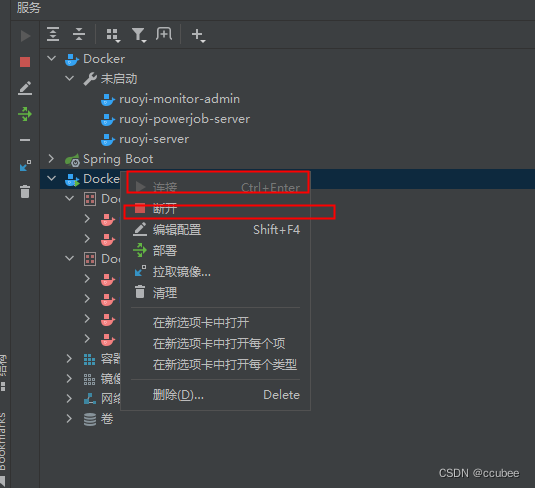
记录ruoyi-plus-vue部署的问题
ruoyi-vue-plus5.x 后端 ruoyi-vue-plus5.x 前端 前端本地启动命令 # 克隆项目 git clone https://gitee.com/JavaLionLi/plus-ui.git# 安装依赖 npm install --registryhttps://registry.npmmirror.com# 启动服务 npm run dev# 构建生产环境 yarn build:prod # 前端访问地址…...

如何在springboot项目中使用minio上传下载删除文件
引入maven依赖 <!-- minio --> <dependency><groupId>io.minio</groupId><artifactId>minio</artifactId><version>8.2.2</version> </dependency>申请 bucket | access_key | secret_key 项目中配置相关参数 mini…...
SSM个性化旅游管理系统开发mysql数据库web结构java编程计算机网页源码eclipse项目
一、源码特点 SSM 个性化旅游管理系统是一套完善的信息系统,结合springMVC框架完成本系统,对理解JSP java编程开发语言有帮助系统采用SSM框架(MVC模式开发),系统具有完整的源代码和数据库 ,系统主要采用B…...

4-Docker命令之docker version
1.docker version介绍 docker version命令是用于查看docker容器的版本信息 2.docker version用法 docker version [参数] [root@centos79 ~]# docker version --helpUsage: docker version [OPTIONS]Show the Docker version informationOptions:-f, --format string Fo…...
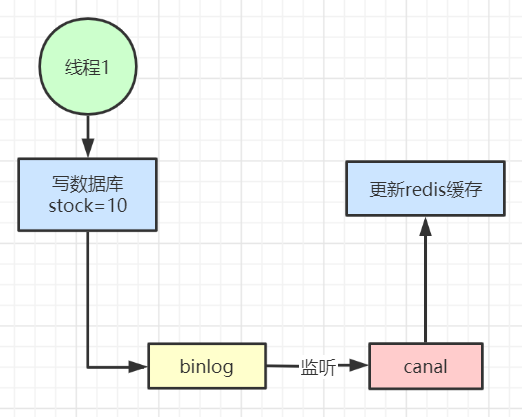
Redis高并发缓存架构
前言: 针对缓存我们并不陌生,而今天所讲的是使用redis作为缓存工具进行缓存数据。redis缓存是将数据保存在内存中的,而内存的珍贵性是不可否认的。所以在缓存之前,我们需要明确缓存的对象,是否有必要缓存,怎…...

谨防利用Redis未授权访问漏洞入侵服务器
说明: Redis是一个开源的,由C语言编写的高性能NoSQL数据库,因其高性能、可扩展、兼容性强,被各大小互联网公司或个人作为内存型存储组件使用。 但是其中有小部分公司或个人开发者,为了方便调试或忽略了安全风险&#…...
关于一些bug的解决1、el-input的输入无效2、搜索之后发现数据不对3、el多选框、单选框点击无用4、
el-input输入无效 原来的代码是 var test null 但是我发现不能输入任何值 反倒修改test的初始值为123是可以的 于是我确定绑定没问题 就是修改的问题 于是改成 var test ref() v-model绑定的值改成test.value就可以了 因为ref是相应式的 可以通过输入…...

使用 JavaScript 进行 API 测试的综合教程
说明 API 测试是软件测试的一种形式,涉及直接测试 API 并作为集成测试的一部分,以确定它们是否满足功能、可靠性、性能和安全性的预期。 先决条件: JavaScript 基础知识。Node.js 安装在您的计算机上。如果没有,请在此处下载。npm…...
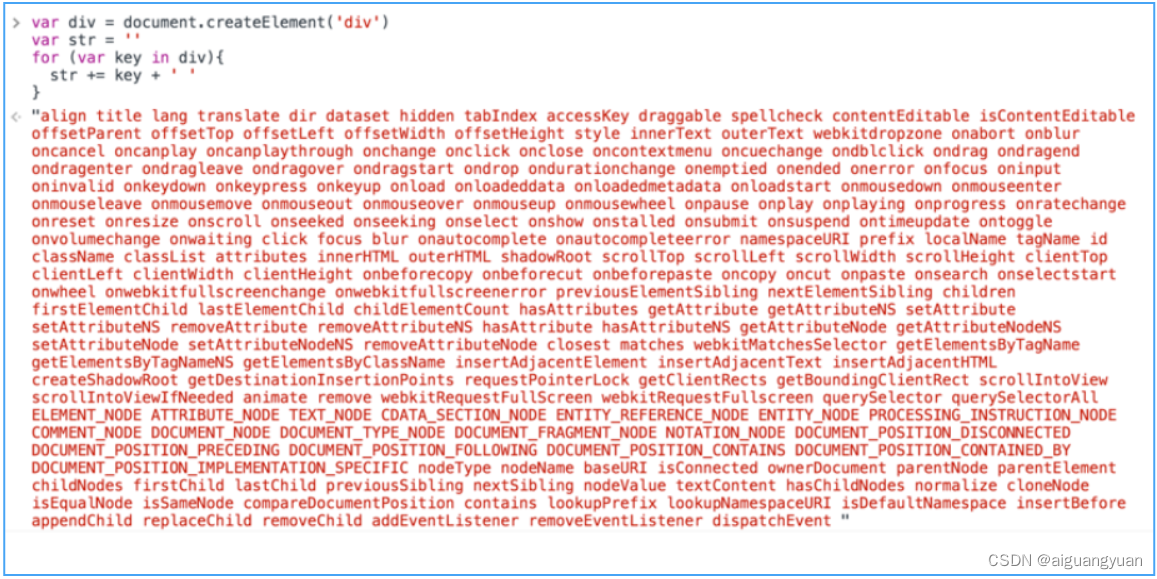
Vue 2.0源码分析-Virtual DOM
Virtual DOM 这个概念相信大部分人都不会陌生,它产生的前提是浏览器中的 DOM 是很“昂贵"的,为了更直观的感受,我们可以简单的把一个简单的 div 元素的属性都打印出来,如图所示: 可以看到,真正的 DOM …...
freeRTOS移植STMF103)
(HAL库版)freeRTOS移植STMF103
正点原子关于freeRTOS的教程是比较好的,可惜移植的是标准库,但是我学的是Hal库,因为开发速度更快,从最后那个修改SYSTEM文件夹的地方开始替换为下面的内容就可以了 5.修改Systick中断、SVC中断、PendSV中断 将SVC中断、P…...

vue2-axios
下载axios 开发版本:axios.js 生产版本:axios.min.js 搭建服务器:json-server npm i -g json-serverjson-server --watch db.json(启动服务并读取文件,db.json文件目录下启动) json-server --watch db.j…...
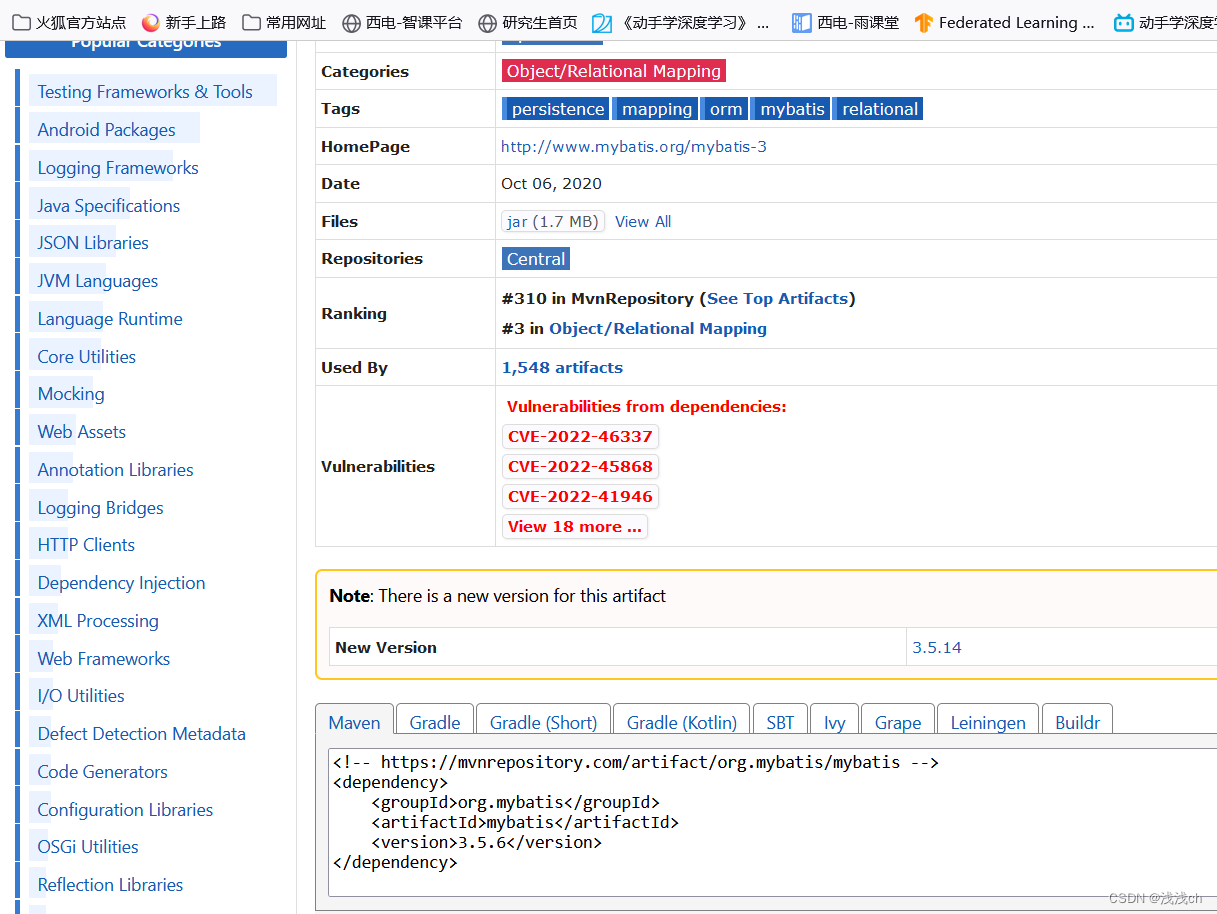
创建maven的web项目
(一)创建maven的web项目 Step1、创建一个普通的maven项目 (1)新建一个empty project,命名为SSM2。 点击项目名,右键new,选择Module,左侧选择“Maven archetype”,可以给…...

使用uniapp开发系统懒加载图片效果
1、创建一个Vue组件 在uniapp项目中,我们可以创建一个独立的Vue组件来实现懒加载图片效果。打开uniapp项目,进入components文件夹,创建一个名为"LazeImage"的组件。 2、编写组件模板 在"LazeImage"组件中,…...

导入PIL时报错
在导入PIL时,报以下错误: 查找原因 参考博客 Could not find a version that satisfies the requirement PIL (from versions: ) No matching distributi-CSDN博客,按照wheel后,安装PIL时,报如下的错误。 查找说是python版本与wheel文件版本不同,确认本机python版本 …...

【Linux】shell脚本忽略错误继续执行
在 shell 脚本中,可以使用 set -e 命令来设置脚本在遇到错误时退出执行。如果你希望脚本忽略错误并继续执行,可以在脚本开头添加 set e 命令来取消该设置。 举例1 #!/bin/bash# 取消 set -e 的设置 set e# 执行命令,并忽略错误 rm somefile…...

ES6从入门到精通:前言
ES6简介 ES6(ECMAScript 2015)是JavaScript语言的重大更新,引入了许多新特性,包括语法糖、新数据类型、模块化支持等,显著提升了开发效率和代码可维护性。 核心知识点概览 变量声明 let 和 const 取代 var…...

FFmpeg 低延迟同屏方案
引言 在实时互动需求激增的当下,无论是在线教育中的师生同屏演示、远程办公的屏幕共享协作,还是游戏直播的画面实时传输,低延迟同屏已成为保障用户体验的核心指标。FFmpeg 作为一款功能强大的多媒体框架,凭借其灵活的编解码、数据…...

DAY 47
三、通道注意力 3.1 通道注意力的定义 # 新增:通道注意力模块(SE模块) class ChannelAttention(nn.Module):"""通道注意力模块(Squeeze-and-Excitation)"""def __init__(self, in_channels, reduction_rat…...

React19源码系列之 事件插件系统
事件类别 事件类型 定义 文档 Event Event 接口表示在 EventTarget 上出现的事件。 Event - Web API | MDN UIEvent UIEvent 接口表示简单的用户界面事件。 UIEvent - Web API | MDN KeyboardEvent KeyboardEvent 对象描述了用户与键盘的交互。 KeyboardEvent - Web…...

2025 后端自学UNIAPP【项目实战:旅游项目】6、我的收藏页面
代码框架视图 1、先添加一个获取收藏景点的列表请求 【在文件my_api.js文件中添加】 // 引入公共的请求封装 import http from ./my_http.js// 登录接口(适配服务端返回 Token) export const login async (code, avatar) > {const res await http…...

解决本地部署 SmolVLM2 大语言模型运行 flash-attn 报错
出现的问题 安装 flash-attn 会一直卡在 build 那一步或者运行报错 解决办法 是因为你安装的 flash-attn 版本没有对应上,所以报错,到 https://github.com/Dao-AILab/flash-attention/releases 下载对应版本,cu、torch、cp 的版本一定要对…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现录音机应用
1. 项目配置与权限设置 1.1 配置module.json5 {"module": {"requestPermissions": [{"name": "ohos.permission.MICROPHONE","reason": "录音需要麦克风权限"},{"name": "ohos.permission.WRITE…...
)
OpenLayers 分屏对比(地图联动)
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 地图分屏对比在WebGIS开发中是很常见的功能,和卷帘图层不一样的是,分屏对比是在各个地图中添加相同或者不同的图层进行对比查看。…...
Reasoning over Uncertain Text by Generative Large Language Models
https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829 1. 概述 文本中的不确定性在许多语境中传达,从日常对话到特定领域的文档(例如医学文档)(Heritage 2013;Landmark、Gulbrandsen 和 Svenevei…...
