竞赛选题 题目:基于FP-Growth的新闻挖掘算法系统的设计与实现
文章目录
- 0 前言
- 1 项目背景
- 2 算法架构
- 3 FP-Growth算法原理
- 3.1 FP树
- 3.2 算法过程
- 3.3 算法实现
- 3.3.1 构建FP树
- 3.4 从FP树中挖掘频繁项集
- 4 系统设计展示
- 5 最后
0 前言
🔥 优质竞赛项目系列,今天要分享的是
基于FP-Growth的新闻挖掘算法系统的设计与实现
该项目较为新颖,适合作为竞赛课题方向,学长非常推荐!
🧿 更多资料, 项目分享:
https://gitee.com/dancheng-senior/postgraduate
1 项目背景
如今新闻泛滥,令人眼花缭乱,即使同一话题下的新闻也多得数不胜数。人们可以根据自己的职业和爱好关注专业新闻网站的不同热点要闻。因此,通过对人们关注新闻的热点问题进行分析,可以得出民众对某个领域的关切程度和社会需要解决的问题,也有利于了解当前的舆论焦点,有助于政府了解民意,便于国家对舆论进行正确引导,使我们的社会更加安定和谐。本文以财经领域为例,通过爬虫技术抓取网络上的大量财经新闻,通过对新闻内容文本进行预处理及密度聚类分析来发现热点;从发现的热点中,再进行词汇聚类分析,得出热点所涉及的人或事物,以此分析出社会对经济领域关注的问题和需要解决的问题。

2 算法架构
该项目学长要通过文本挖掘技术进行新闻热点问题分析,把从网上抓取到的财经新闻,通过对新闻内容的聚类,得到新闻热点;再对热点进行分析,通过对某一热点相关词汇的聚类,得到热点问题所涉及的人物、行业或组织等。

1、利用新闻 API、爬虫算法、多线程并行技术,抓取三大专业财经新闻网站(新浪财经、搜狐财经、新华网财经)的大量财经新闻报道;
2、对新闻进行去重、时间段过滤,然后对新闻内容文本进行 jieba
分词并词性标注,过滤出名词、动词、简称等词性,分词前使用自定义的用户词词典增加分词的准确性,分词后使用停用词词典、消歧词典、保留单字词典过滤掉对话题无关并且影响聚类准确性的词,建立每篇新闻的词库,利用
TF-IDF 特征提取之后对新闻进行 DBSCAN 聚类,并对每个类的大小进行排序;
3、针对聚类后的每一类新闻,为了得到该处热点的话题信息,还需要提取它们的标题,利用 TextRank
算法,对标题的重要程度进行排序,用重要性最高的标题来描述该处热点的话题
4、对所有的新闻内容进行 jieba 分词,并训练出 word2vec 词嵌入模型,然后对聚类后的每一类新闻,提取它们的内容分词后的结果,运用
word2vec 模型得到每个词的词向量,再利用 FP-Growth类算法进行相关新闻挖掘。
3 FP-Growth算法原理
3.1 FP树
FP树是一种存储数据的树结构,如下图所示,每一路分支表示数据集的一个项集,数字表示该元素在某分支中出现的次数

3.2 算法过程
1 构建FP树
- 遍历数据集获得每个元素项的出现次数,去掉不满足最小支持度的元素项
- 构建FP树:读入每个项集并将其添加到一条已存在的路径中,若该路径不存在,则创建一条新路径(每条路径是一个无序集合)
2 从FP树中挖掘频繁项集
- 从FP树中获得条件模式基
- 利用条件模式基构建相应元素的条件FP树,迭代直到树包含一个元素项为止
算法过程写得比较简略,具体过程我们在下节的实操中进一步理解。
3.3 算法实现
3.3.1 构建FP树
class treeNode:def __init__(self,nameValue,numOccur,parentNode):self.name=nameValue #节点名self.count=numOccur #节点元素出现次数self.nodeLink=None #存放节点链表中,与该节点相连的下一个元素self.parent=parentNodeself.children={} #用于存放节点的子节点,value为子节点名def inc(self,numOccur):self.count+=numOccurdef disp(self,ind=1):print(" "*ind,self.name,self.count) #输出一行节点名和节点元素数,缩进表示该行节点所处树的深度for child in self.children.values():child.disp(ind+1) #对于子节点,深度+1# 构造FP树# dataSet为字典类型,表示探索频繁项集的数据集,keys为各项集,values为各项集在数据集中出现的次数# minSup为最小支持度,构造FP树的第一步是计算数据集各元素的支持度,选择满足最小支持度的元素进入下一步def createTree(dataSet,minSup=1):headerTable={}#遍历各项集,统计数据集中各元素的出现次数for key in dataSet.keys():for item in key:headerTable[item]=headerTable.get(item,0)+dataSet[key] #遍历各元素,删除不满足最小支持度的元素for key in list(headerTable.keys()):if headerTable[key]<minSup:del headerTable[key]freqItemSet=set(headerTable.keys())#若没有元素满足最小支持度要求,返回None,结束函数if len(freqItemSet)==0:return None,Nonefor key in headerTable.keys():headerTable[key]=[headerTable[key],None] #[元素出现次数,**指向每种项集第一个元素项的指针**]retTree=treeNode("Null Set",1,None) #初始化FP树的顶端节点for tranSet,count in dataSet.items():localD={} #存放每次循环中的频繁元素及其出现次数,便于利用全局出现次数对各项集元素进行项集内排序for item in tranSet:if item in freqItemSet:localD[item]=headerTable[item][0]if len(localD)>0:orderedItems=[v[0] for v in sorted(localD.items(),key=operator.itemgetter(1),reverse=True)] #根据元素全局出现次数对每个项集(tranSet)中的元素进行排序updateTree(orderedItems,retTree,headerTable,count) #使用排序后的项集对树进行填充return retTree,headerTable#树的更新函数#items为按出现次数排序后的项集,是待更新到树中的项集;count为items项集在数据集中的出现次数#inTree为待被更新的树;headTable为头指针表,存放满足最小支持度要求的所有元素def updateTree(items,inTree,headerTable,count):#若项集items当前最频繁的元素在已有树的子节点中,则直接增加树子节点的计数值,增加值为items[0]的出现次数if items[0] in inTree.children: inTree.children[items[0]].inc(count)else:#若项集items当前最频繁的元素不在已有树的子节点中(即,树分支不存在),则通过treeNode类新增一个子节点inTree.children[items[0]]=treeNode(items[0],count,inTree)#若新增节点后表头表中没有此元素,则将该新增节点作为表头元素加入表头表if headerTable[items[0]][1]==None: headerTable[items[0]][1]=inTree.children[items[0]]else:#若新增节点后表头表中有此元素,则更新该元素的链表,即,在该元素链表末尾增加该元素updateHeader(headerTable[items[0]][1],inTree.children[items[0]])#对于项集items元素个数多于1的情况,对剩下的元素迭代updateTreeif len(items)>1:updateTree(items[1::],inTree.children[items[0]],headerTable,count)#元素链表更新函数#nodeToTest为待被更新的元素链表的头部#targetNode为待加入到元素链表的元素节点def updateHeader(nodeToTest,targetNode):#若待被更新的元素链表当前元素的下一个元素不为空,则一直迭代寻找该元素链表的末位元素while nodeToTest.nodeLink!=None: nodeToTest=nodeToTest.nodeLink #类似撸绳子,从首位一个一个逐渐撸到末位#找到该元素链表的末尾元素后,在此元素后追加targetNode为该元素链表的新末尾元素nodeToTest.nodeLink=targetNode测试
#加载简单数据集
def loadSimpDat():simpDat = [['r', 'z', 'h', 'j', 'p'],['z', 'y', 'x', 'w', 'v', 'u', 't', 's'],['z'],['r', 'x', 'n', 'o', 's'],['y', 'r', 'x', 'z', 'q', 't', 'p'],['y', 'z', 'x', 'e', 'q', 's', 't', 'm']]return simpDat#将列表格式的数据集转化为字典格式
def createInitSet(dataSet):retDict={}for trans in dataSet:retDict[frozenset(trans)]=1return retDictsimpDat=loadSimpDat()
dataSet=createInitSet(simpDat)
myFPtree1,myHeaderTab1=createTree(dataSet,minSup=3)
myFPtree1.disp(),myHeaderTab1
输入数据:

由此数据集构建的FP树长这样,看看是不是满足上一节介绍的FP树结构

3.4 从FP树中挖掘频繁项集
具体过程如下:
1 从FP树中获得条件模式基
- 条件模式基:以所查找元素项为结尾的路径集合,每条路径都是一条前缀路径,路径集合包括前缀路径和路径计数值。
- 例如,元素"r"的条件模式基为 {x,s}2,{z,x,y}1,{z}1
- 前缀路径:介于所查找元素和树根节点之间的所有内容
- 路径计数值:等于该条前缀路径的起始元素项(即所查找的元素)的计数值
2 利用条件模式基构建相应元素的条件FP树
- 对每个频繁项,都要创建一棵条件FP树。
- 例如对元素t创建条件FP树:使用获得的t元素的条件模式基作为输入,利用构建FP树相同的逻辑构建元素t的条件FP树
3 迭代步骤(1)(2),直到树包含一个元素项为止
-
接下来继续构建{t,x}{t,y}{t,z}对应的条件FP树(tx,ty,tz为t条件FP树的频繁项集),直到条件FP树中没有元素为止
-
至此可以得到与元素t相关的频繁项集,包括2元素项集、3元素项集。。。
#由叶节点回溯该叶节点所在的整条路径 #leafNode为叶节点,treeNode格式;prefixPath为该叶节点的前缀路径集合,列表格式,在调用该函数前注意prefixPath的已有内容 def ascendTree(leafNode,prefixPath):if leafNode.parent!=None:prefixPath.append(leafNode.name)ascendTree(leafNode.parent,prefixPath)#获得指定元素的条件模式基 #basePat为指定元素;treeNode为指定元素链表的第一个元素节点,如指定"r"元素,则treeNode为r元素链表的第一个r节点 def findPrefixPath(basePat,treeNode):condPats={} #存放指定元素的条件模式基while treeNode!=None: #当元素链表指向的节点不为空时(即,尚未遍历完指定元素的链表时)prefixPath=[]ascendTree(treeNode,prefixPath) #回溯该元素当前节点的前缀路径if len(prefixPath)>1:condPats[frozenset(prefixPath[1:])]=treeNode.count #构造该元素当前节点的条件模式基treeNode=treeNode.nodeLink #指向该元素链表的下一个元素return condPats#有FP树挖掘频繁项集 #inTree: 构建好的整个数据集的FP树 #headerTable: FP树的头指针表 #minSup: 最小支持度,用于构建条件FP树 #preFix: 新增频繁项集的缓存表,set([])格式 #freqItemList: 频繁项集集合,list格式def mineTree(inTree,headerTable,minSup,preFix,freqItemList):#按头指针表中元素出现次数升序排序,即,从头指针表底端开始寻找频繁项集bigL=[v[0] for v in sorted(headerTable.items(),key=lambda p:p[1][0])] for basePat in bigL:#将当前深度的频繁项追加到已有频繁项集中,然后将此频繁项集追加到频繁项集列表中newFreqSet=preFix.copy()newFreqSet.add(basePat)print("freqItemList add newFreqSet",newFreqSet)freqItemList.append(newFreqSet)#获取当前频繁项的条件模式基condPatBases=findPrefixPath(basePat,headerTable[basePat][1])#利用当前频繁项的条件模式基构建条件FP树myCondTree,myHead=createTree(condPatBases,minSup)#迭代,直到当前频繁项的条件FP树为空if myHead!=None:mineTree(myCondTree,myHead,minSup,newFreqSet,freqItemList)
接着刚才构建的FP树,测试一下,
freqItems=[]
mineTree(myFPtree1,myHeaderTab1,3,set([]),freqItems)
freqItems
我们从FP树中挖掘到的频繁项集如下,这里设置的最小支持度为3:

上图表示数据集中,支持度大于3(出现3次以上)的元素项集,即,频繁项集。
4 系统设计展示
为了方便操作及理解,学长使用 Python 的 tkinter 模块设计了一个系统操作界面

分析可视化




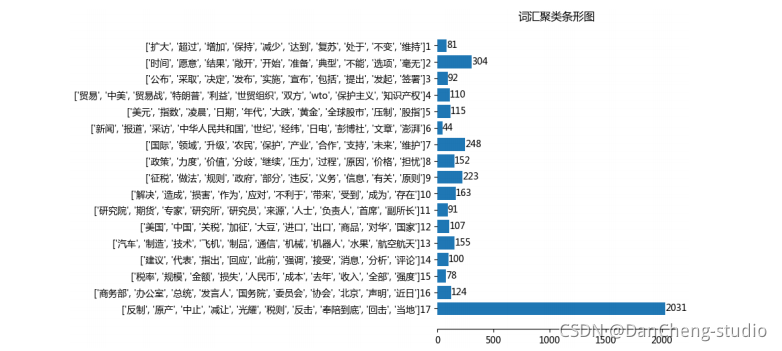
(未完待续。。。。)
5 最后
🧿 更多资料, 项目分享:
https://gitee.com/dancheng-senior/postgraduate
相关文章:

竞赛选题 题目:基于FP-Growth的新闻挖掘算法系统的设计与实现
文章目录 0 前言1 项目背景2 算法架构3 FP-Growth算法原理3.1 FP树3.2 算法过程3.3 算法实现3.3.1 构建FP树 3.4 从FP树中挖掘频繁项集 4 系统设计展示5 最后 0 前言 🔥 优质竞赛项目系列,今天要分享的是 基于FP-Growth的新闻挖掘算法系统的设计与实现…...

188. 股票买卖问题(交易次数为任意正整数)
题目 题解 class Solution:def maxProfit(self, k: int, prices: List[int]) -> int:N len(prices)# 定义状态:dp[i][j][k]表示在第i天,有j次交易机会,持有或不持有的最大利润dp [[[0 for i in range(2)] for j in range(k1)] for m in range(N)]f…...

Typescript怎样对URL参数进行编码?
URL中的参数需要进行编码(URL encoding)是为了确保传输的参数不包含特殊字符,同时确保数据的可靠性和安全性。 特殊字符如空格、&、?等在URL中有特殊含义,如果直接包含在参数值中,可能会导致解析错误或者安全问题…...
AndroidStudio2022.3.1 Patch3使用国内下载源加速
记录一下这个版本的as在使用国内下载源加速碰到的诸多问题。 一、gradle-8.0-bin.zip下载慢 编辑项目文件夹/gradle/wrapper/gradle-wrapper.properties,文件内容改为如下: #Fri Nov 24 18:50:06 CST 2023 distributionBaseGRADLE_USER_HOME distribu…...

Go语言的学习笔记2——Go语言源文件的结构布局
用一个只有main函数的go文件来简单说一下Go语言的源文件结构布局,主要分为包名、引入的包和具体函数。下边是main.go示例代码: package mainimport "fmt"func main() { fmt.Println("hello, world") }package main就是表明这个文件…...

python给视频增加字幕
python给视频增加字幕 安装所需库 在开始之前,我们需要安装一些Python库。主要使用到的库如下: moviepy:用于处理视频和音频的库。 pydub:用于处理音频的库。 speech_recognition:用于语音识别的库。 首先࿰…...
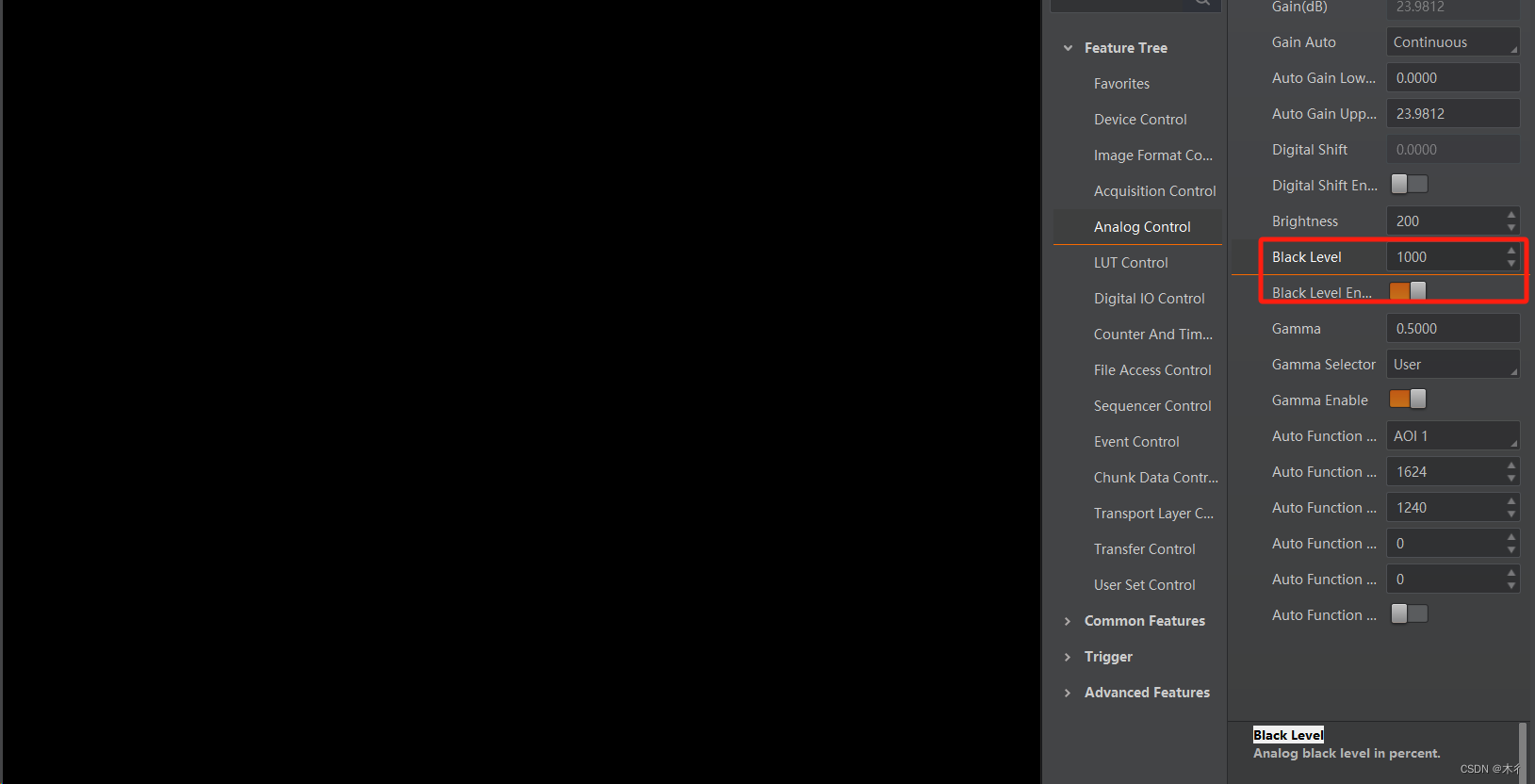
相机设置参数:黑电平(Black Level)详解和示例
本文通过原理和示例对相机设置参数“黑电平”进行讲解,以帮助大家理解和使用。 原理 相机中黑电平原理是将电平增大,可以显示更多暗区细节,可能会损失一些亮区,但图像更多的关注暗区,获取完图像信息再减掉。只是为了…...
Mac Ubuntu双系统解决WiFi和WiFi 5G网络不可用问题
文章目录 设备信息1. Ubuntu WiFi不可用解决方式查看Mac的网卡型号根据网卡型号搜索获取到的解决方法查看WiFi名字问题参考链接 2. 解决WiFi重启后失效问题打开终端创建.sh脚本文件编辑脚本文件复制粘贴脚本修改脚本权限创建并编辑systemd service文件复制粘贴下文到systemd se…...
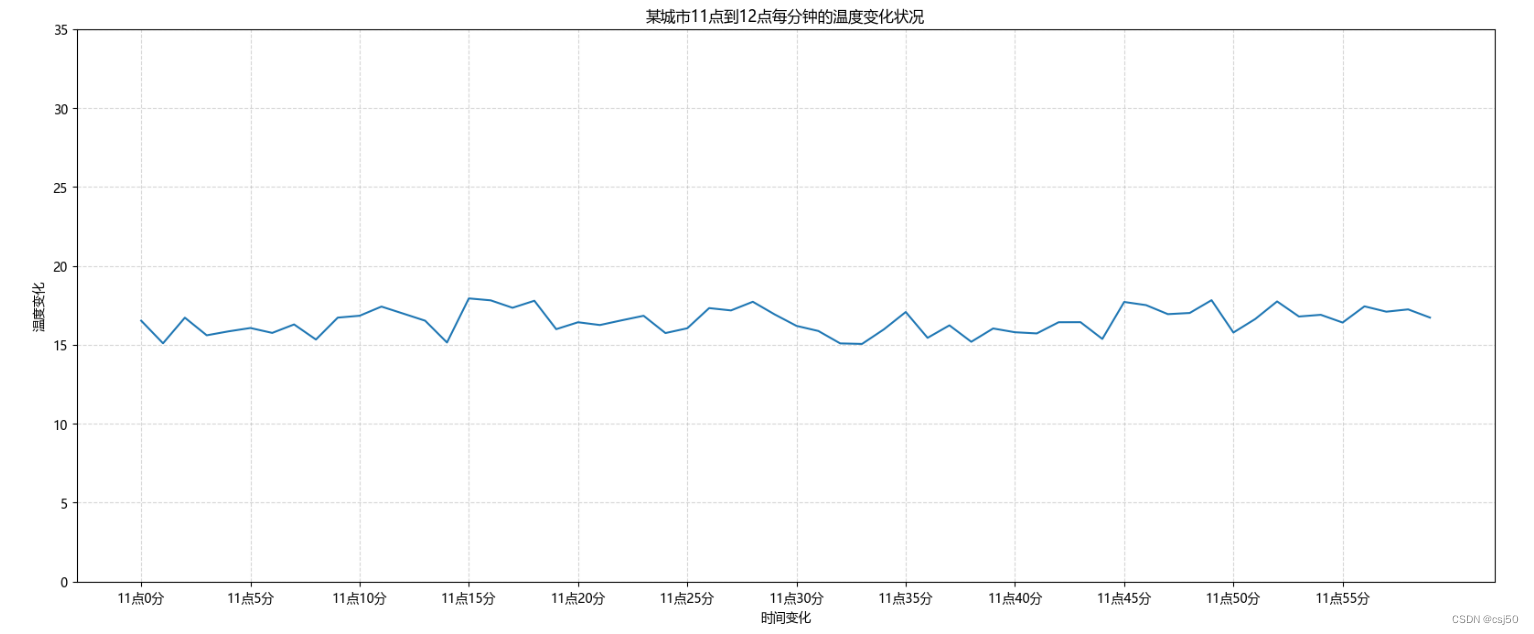
数据分析基础之《matplotlib(2)—折线图》
一、折线图绘制与保存图片 1、matplotlib.pyplot模块 matplotlib.pyplot包含了一系列类似于matlab的画图函数。它的函数作用于当前图形(figure)的当前坐标系(axes) import matplotlib.pyplot as plt 2、折线图绘制与显示 展示城…...
 - 函数与模块系统)
Rust语言入门教程(三) - 函数与模块系统
函数 函数的定义 根据Rust的格式规范,函数名的格式应遵从蛇形命名法,即是用小写字母以及下划线组成,如: fn do_stuff(){ }Rust并不要求函数定义的位置必须在调用它之前,所以如果你习惯于把main函数放在最前面的话&a…...
ubuntu22.04 arrch64版在线安装java环境
脚本 #安装java#!/bin/bashif type -p java; thenecho "Java has been installed."else#2.Installed Java , must install wgetwget -c https://repo.huaweicloud.com/java/jdk/8u151-b12/jdk-8u151-linux-arm64-vfp-hflt.tar.gz;tar -zxvf ./jdk-8u151-linux-arm6…...
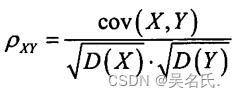
概率论与数理统计中常见的随机变量分布律、数学期望、方差及其介绍
1 离散型随机变量 1.1 0-1分布 设随机变量X的所有可能取值为0与1两个值,其分布律为 若分布律如上所示,则称X服从以P为参数的(0-1)分布或两点分布。记作X~ B(1,p) 0-1分布的分布律利用表格法表示为: X01P1-PP 0-1分布的数学期望E(X) 0 *…...

骨传导耳机的优缺点都有哪些?骨传导耳机值得入手吗?
骨传导耳机的优点还是很多的,相比于传统耳机,骨传导耳机要更值得入手! 下面让我们了解下骨传导耳机的优缺点都有哪些: 一、优点 1、使用更安全 传统的耳机,在使用时会听不到外界的声音,而骨传导耳机通过…...
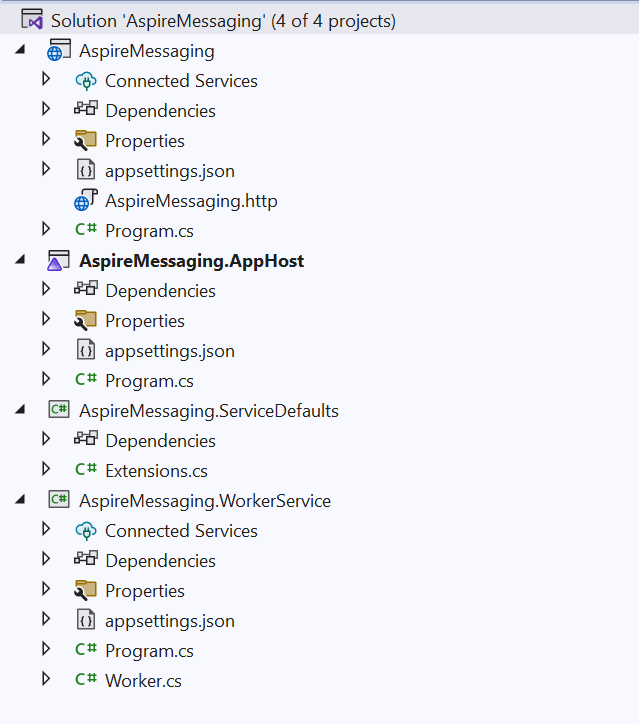
在ASP.NET Core 中使用 .NET Aspire 消息传递组件
前言 云原生应用程序通常需要可扩展的消息传递解决方案,以提供消息队列、主题和订阅等功能。.NET Aspire 组件简化了连接到各种消息传递提供程序(例如 Azure 服务总线)的过程。在本教程中,小编将为大家介绍如何创建一个 ASP.NET …...
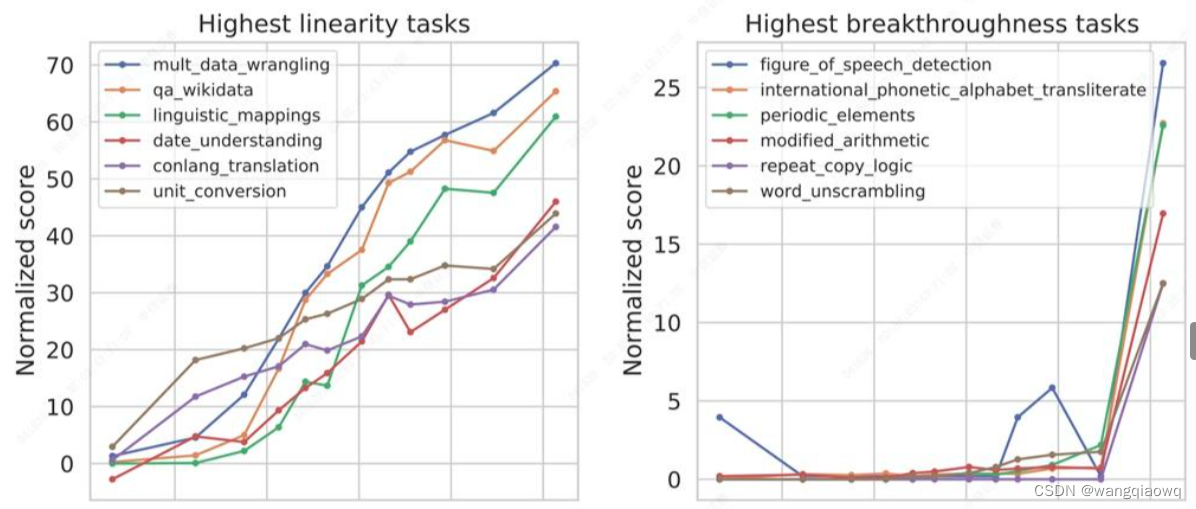
NLP学习
参考:NLP发展之路I - 从词袋模型到Transformer - 知乎 (zhihu.com) NLP大致的发展历史。从最开始的词袋模型,到RNN,到Transformers和BERT,再到ChatGPT,NLP经历了一段不断精进的发展道路。数据驱动和不断完善的端到端的…...

Linux-Ubuntu环境下搭建SVN服务器
Linux-Ubuntu环境下搭建SVN服务器 一、背景二、前置工作2.1确定IP地址保持不变2.2关闭防火墙 三、安装SVN服务器四、修改SVN服务器版本库目录五、调整SVN配置5.1查看需要修改的配置文件5.2修改svnserve.conf文件5.3修改passwd文件,添加账号和密码(window…...
)
python tkinter使用(四)
本篇文章主要讲下tkinter 的文本框相关. tkinter中用Entry来实现输入框,类似于android中的edittext. 具体的用法如下: 1:空白输入框 如下: name tk.Entry(window) name.pack()2: 设置输入框的默认文案 name tk.Entry(window) name.pack() name.insert(tk.END, "请…...
记录ruoyi-plus-vue部署的问题
ruoyi-vue-plus5.x 后端 ruoyi-vue-plus5.x 前端 前端本地启动命令 # 克隆项目 git clone https://gitee.com/JavaLionLi/plus-ui.git# 安装依赖 npm install --registryhttps://registry.npmmirror.com# 启动服务 npm run dev# 构建生产环境 yarn build:prod # 前端访问地址…...

如何在springboot项目中使用minio上传下载删除文件
引入maven依赖 <!-- minio --> <dependency><groupId>io.minio</groupId><artifactId>minio</artifactId><version>8.2.2</version> </dependency>申请 bucket | access_key | secret_key 项目中配置相关参数 mini…...
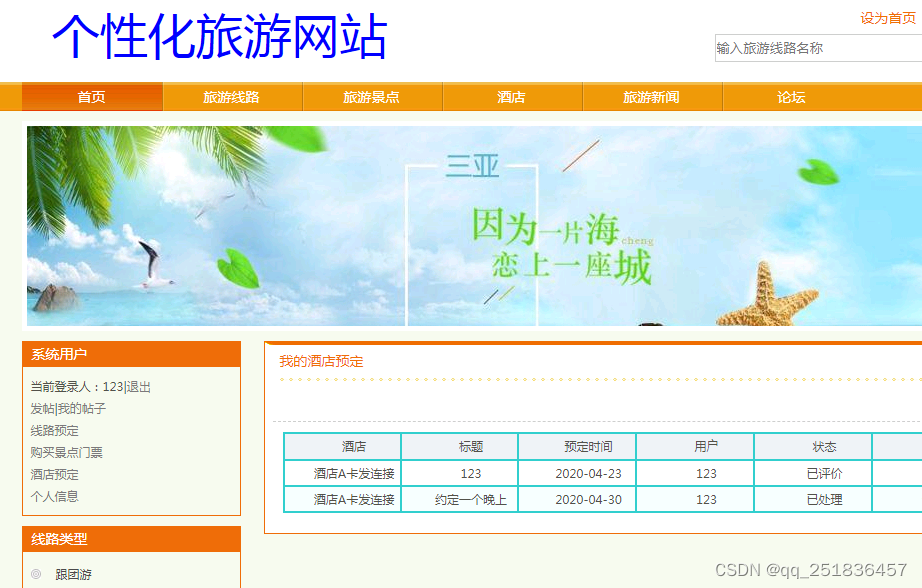
SSM个性化旅游管理系统开发mysql数据库web结构java编程计算机网页源码eclipse项目
一、源码特点 SSM 个性化旅游管理系统是一套完善的信息系统,结合springMVC框架完成本系统,对理解JSP java编程开发语言有帮助系统采用SSM框架(MVC模式开发),系统具有完整的源代码和数据库 ,系统主要采用B…...

华为云AI开发平台ModelArts
华为云ModelArts:重塑AI开发流程的“智能引擎”与“创新加速器”! 在人工智能浪潮席卷全球的2025年,企业拥抱AI的意愿空前高涨,但技术门槛高、流程复杂、资源投入巨大的现实,却让许多创新构想止步于实验室。数据科学家…...

【网络】每天掌握一个Linux命令 - iftop
在Linux系统中,iftop是网络管理的得力助手,能实时监控网络流量、连接情况等,帮助排查网络异常。接下来从多方面详细介绍它。 目录 【网络】每天掌握一个Linux命令 - iftop工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景…...

UDP(Echoserver)
网络命令 Ping 命令 检测网络是否连通 使用方法: ping -c 次数 网址ping -c 3 www.baidu.comnetstat 命令 netstat 是一个用来查看网络状态的重要工具. 语法:netstat [选项] 功能:查看网络状态 常用选项: n 拒绝显示别名&#…...

全球首个30米分辨率湿地数据集(2000—2022)
数据简介 今天我们分享的数据是全球30米分辨率湿地数据集,包含8种湿地亚类,该数据以0.5X0.5的瓦片存储,我们整理了所有属于中国的瓦片名称与其对应省份,方便大家研究使用。 该数据集作为全球首个30米分辨率、覆盖2000–2022年时间…...

让AI看见世界:MCP协议与服务器的工作原理
让AI看见世界:MCP协议与服务器的工作原理 MCP(Model Context Protocol)是一种创新的通信协议,旨在让大型语言模型能够安全、高效地与外部资源进行交互。在AI技术快速发展的今天,MCP正成为连接AI与现实世界的重要桥梁。…...

SpringCloudGateway 自定义局部过滤器
场景: 将所有请求转化为同一路径请求(方便穿网配置)在请求头内标识原来路径,然后在将请求分发给不同服务 AllToOneGatewayFilterFactory import lombok.Getter; import lombok.Setter; import lombok.extern.slf4j.Slf4j; impor…...

Swagger和OpenApi的前世今生
Swagger与OpenAPI的关系演进是API标准化进程中的重要篇章,二者共同塑造了现代RESTful API的开发范式。 本期就扒一扒其技术演进的关键节点与核心逻辑: 🔄 一、起源与初创期:Swagger的诞生(2010-2014) 核心…...

Python 实现 Web 静态服务器(HTTP 协议)
目录 一、在本地启动 HTTP 服务器1. Windows 下安装 node.js1)下载安装包2)配置环境变量3)安装镜像4)node.js 的常用命令 2. 安装 http-server 服务3. 使用 http-server 开启服务1)使用 http-server2)详解 …...

适应性Java用于现代 API:REST、GraphQL 和事件驱动
在快速发展的软件开发领域,REST、GraphQL 和事件驱动架构等新的 API 标准对于构建可扩展、高效的系统至关重要。Java 在现代 API 方面以其在企业应用中的稳定性而闻名,不断适应这些现代范式的需求。随着不断发展的生态系统,Java 在现代 API 方…...

WPF八大法则:告别模态窗口卡顿
⚙️ 核心问题:阻塞式模态窗口的缺陷 原始代码中ShowDialog()会阻塞UI线程,导致后续逻辑无法执行: var result modalWindow.ShowDialog(); // 线程阻塞 ProcessResult(result); // 必须等待窗口关闭根本问题:…...
