基础存贮模型介绍
基础存贮模型
这里主要讨论在需求量稳定的情况下,贮存量需要多少的问题。当贮存量过大时,会提高库存成本,也会造成积压资金;当贮存量过小时,会导致一次性订购费用增加,或者不能及时满足需求。 下面讨论不允许缺货的存贮模型:
积压资金: 生产了一批货,但货物在一段时间内都无法卖出变为流动资金。
例1: 若有一个工厂生产货物,每次生产前需要支付生产准备费(是固定的,与货物数量无关),当产量大于需求量时,多余的货物需要放置在仓库中,这时需要支付贮存费。设该货物每日需求量为 nnn 件,生产准备费为 c1c_1c1,每件货物的贮存费为 c2c_2c2,一次性生产 TTT 日的货物,求总费用 CCC 以及每日平均费用 C‾\overline{C}C。
解:
这里生产就算第 111 天,这天也会卖货。
总费用=生产准备费+贮存费总费用=生产准备费+贮存费总费用=生产准备费+贮存费 贮存费穷举法(也可以直接用积分计算)如下表:
| 天数 | 剩余货物数 | 贮存费 |
|---|---|---|
| 111 | n(T−1)n(T-1)n(T−1) | c2n(T−1)c_2n(T-1)c2n(T−1) |
| 222 | n(T−2)n(T-2)n(T−2) | c2n(T−2)c_2n(T-2)c2n(T−2) |
| ⋮\vdots⋮ | ⋮\vdots⋮ | ⋮\vdots⋮ |
| T−1T-1T−1 | nnn | c2nc_2nc2n |
| TTT | 000 | 000 |
贮存费=c2n[(T−1)+(T−2)+⋯+2+1+0]=c2n[(T−1)+0]T2=c2n(T−1)T2贮存费=c_2n[(T-1)+(T-2)+\cdots+2+1+0]=c_2n\frac{[(T-1)+0]T}{2}=c_2n\frac{(T-1)T}{2}贮存费=c2n[(T−1)+(T−2)+⋯+2+1+0]=c2n2[(T−1)+0]T=c2n2(T−1)T 则总费用为: C=c1+c2n(T−1)T2C=c_1+c_2n\frac{(T-1)T}{2}C=c1+c2n2(T−1)T 每日平均费用为:C‾=CT=c1T+c2nT−12\overline{C}=\frac{C}{T}=\frac{c_1}{T}+c_2n\frac{T-1}{2}C=TC=Tc1+c2n2T−1若是生产当天不卖货,则可以将生产当天记为第 000 天,此时的总费用为:C=c1+c2nT22C=c_1+c_2n\frac{T^2}{2}C=c1+c2n2T2 每日平均费用为:C‾=c1T+c2nT2\overline{C}=\frac{c_1}{T}+c_2n\frac{T}{2}C=Tc1+c2n2T
相关文章:

基础存贮模型介绍
基础存贮模型 这里主要讨论在需求量稳定的情况下,贮存量需要多少的问题。当贮存量过大时,会提高库存成本,也会造成积压资金;当贮存量过小时,会导致一次性订购费用增加,或者不能及时满足需求。 下面讨论不允…...

JNDIExploit使用方法
JNDIExploit 一款用于 JNDI注入 利用的工具,大量参考/引用了 Rogue JNDI 项目的代码,支持直接植入内存shell,并集成了常见的bypass 高版本JDK的方式,适用于与自动化工具配合使用。 对 feihong-cs 大佬的项目https://github.com/fe…...

建议一般人不要全职做副业
欢迎关注勤于奋每天12点准时更新国外LEAD相关技术全职做国外LEAD,听起来不错,但是效果不一定好,没有自控力来全职做,基本要废了自己,最好抽时间来做。我现在就是全职做国外LEAD,外加其他一些项目࿰…...

pytorch入门6--数据分析(pandas)
pandas是基于Numpy构建的,提供了众多比NumPy更高级、更直观的数据处理功能,尤其是它的DataFrame数据结构,可以用处理数据库或电子表格的方式来处理分析数据。 使用Pandas前,需导入以下内容: import numpy as np from …...

淘宝API接口开发系列,详情接口参数说明
onebound.taobao.item_get 公共参数 名称类型必须描述keyString是 调用key(必须以GET方式拼接在URL中) 注册Key和secret: https://o0b.cn/anzexi secretString是调用密钥api_nameString是API接口名称(包括在请求地址中࿰…...

keep-alive
keep-alive 是 Vue 的内置组件,当它包裹动态组件时,会缓存不活动的组件实例,而不是销毁它们。 keep-alive 包裹动态组件时,会缓存不活动的组件实例,而不是销毁它们 使用场景 使用原则:当我们在某些场景下…...

Maven的生命周期及常用命令
文章目录1、Maven生命周期1.1、clean生命周期1.2、default生命周期1.3、site生命周期2、Maven常用命令1、Maven生命周期 Maven有三套生命周期系统: 1、clean生命周期 2、default生命周期 3、site生命周期 三套生命周期之间相互独立,每套生命周期包含一…...

【Java开发】JUC基础 03:线程五大状态和主要方法
1 概念介绍📌 五大状态:new:Thread t new Thread(); 线程对象一旦被创建就进入到了新生状态;就绪状态:当调用start()方法,线程立即进入就绪状态,但不意味着立即调度执行;运行状态&a…...

docker打包容器 在另一个机器上运行
1:将运行中的容器变为镜像docker commit 容器id 镜像名(docker commit 89e81386d35e aabbcc)2:将容器打包成tar包docker save -o xxx.tar 镜像名 (当前路径下会生成一个tar的文件)3:将tar包压缩为gz包tar -…...

2023年全国最新保安员精选真题及答案9
百分百题库提供保安员考试试题、保安职业资格考试预测题、保安员考试真题、保安职业资格证考试题库等,提供在线做题刷题,在线模拟考试,助你考试轻松过关。 91.护卫对象在公共场所参加活动前,保安员需要事先(࿰…...

arduino-sentry2之卡片篇
欧克,今天在学生的强烈要求下 我又重启arduino的sentry2调试篇 目前实验结果,可以检测到10张交通卡片 也就是如图所示十张 具体视频如下: https://live.csdn.net/v/279170 具体代码如下: #include <Arduino.h> #include <...
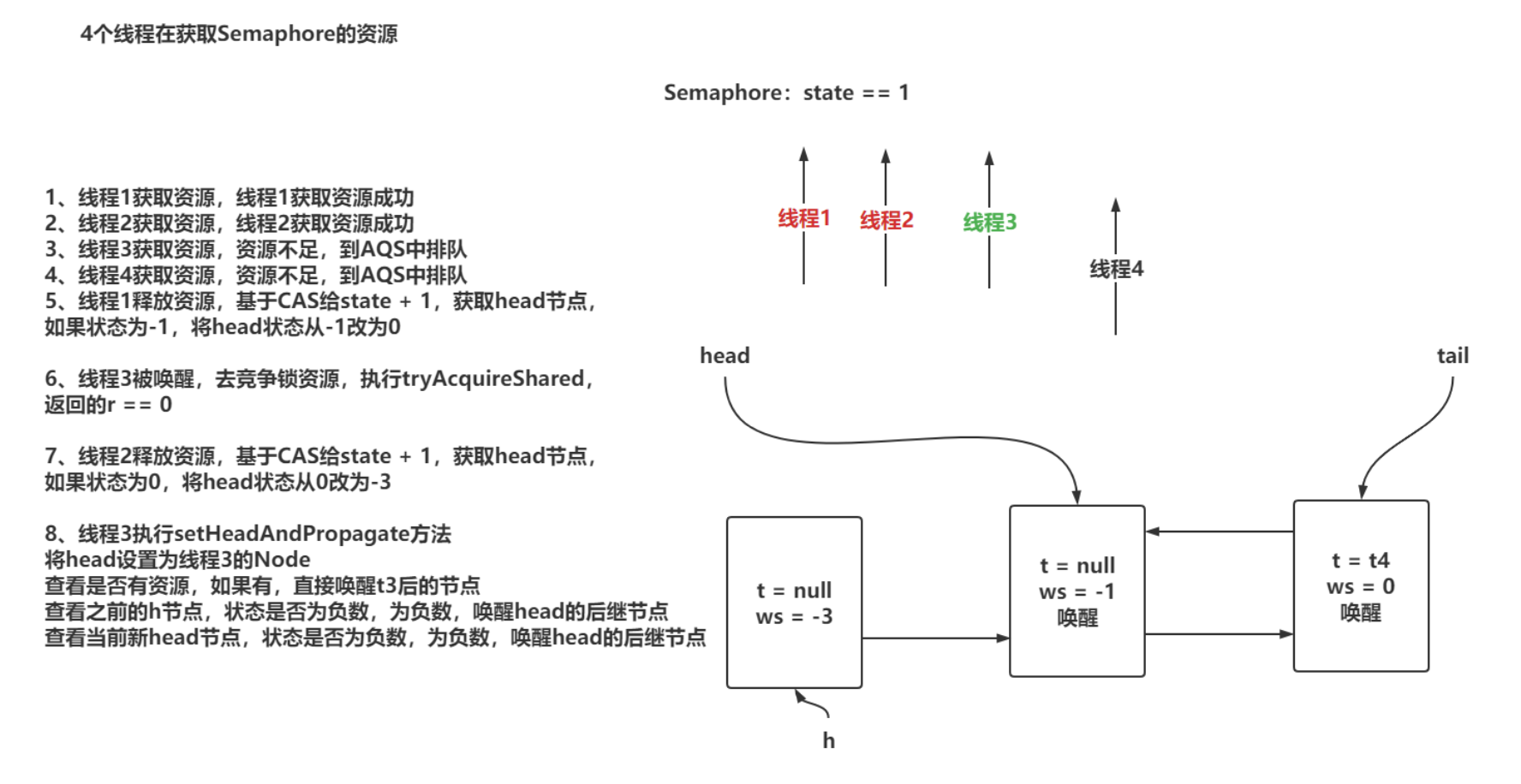
七、JUC并发工具
文章目录JUC并发工具CountDownLatch应用&源码分析CountDownLatch介绍CountDownLatch应用CountDownLatch源码分析有参构造await方法countDown方法CyclicBarrier应用&源码分析CyclicBarrier介绍CyclicBarrier应用CyclicBarrier源码分析CyclicBarrier的核心属性CyclicBarr…...
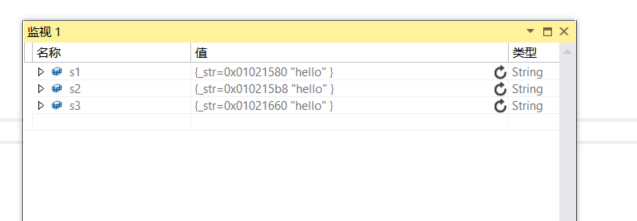
C++ string类(二)及深浅拷贝
一、string类方法使用举例1.迭代器迭代器本质:指针(理解)迭代器:正向迭代器: begin() | end() 反向迭代器: rbegin() | rend()2.find使用//找到s中某个字符 void TestString3() {string s("AAADEFNUIE…...
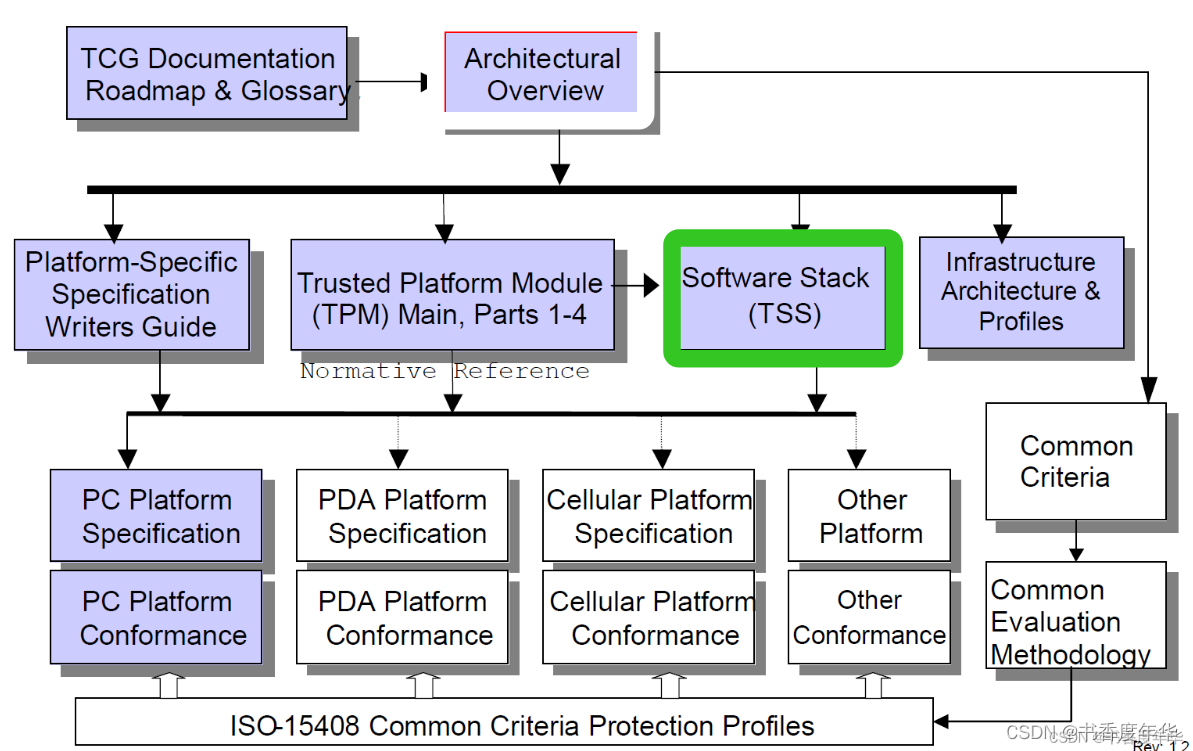
「TCG 规范解读」TCG 软件栈 TSS (上)
可信计算组织(Ttrusted Computing Group,TCG)是一个非盈利的工业标准组织,它的宗旨是加强在相异计算机平台上的计算环境的安全性。TCG于2003年春成立,并采纳了由可信计算平台联盟(the Trusted Computing Platform Alli…...
(二)Markdown编辑器的使用效果 | 以CSDN自带MD编辑器为例
Markdown编辑器使用指南 (一)Markdown编辑器的使用示例 | 以CSDN自带MD编辑器为例(二)Markdown编辑器的使用效果 | 以CSDN自带MD编辑器为例 这里写自定义目录标题欢迎使用Markdown编辑器新的改变功能快捷键合理的创建标题…...

WebSocket网络通信执行流程
目录WebSocket网络通信执行流程相关概念执行流程WebSocket网络通信执行流程 WebSocket协议:通过单个TCP连接在客户端和服务器之间建立全双工双向通信通道。 WebSocket 对象:提供了用于创建和管理 WebSocket 连接,以及可以通过该连接发送和接…...

【Shell学习笔记】4.Shell 基本运算符
前言 本章介绍Shell的基本运算符。 Shell 基本运算符 Shell 和其他编程语言一样,支持多种运算符,包括: 算数运算符关系运算符布尔运算符字符串运算符文件测试运算符 原生bash不支持简单的数学运算,但是可以通过其他命令来实现…...

无代码资讯 | 《低代码开发平台能力要求》发布;CADP列入Gartner《2022-2024 中型企业技术采用路线图》
栏目导读:无代码资讯栏目从全球视角出发,带您了解无代码相关最新资讯。TOP3 大事件1、《低代码开发平台能力要求》团体标准正式发布近日,中国电子工业标准化协会发布公告(中电标【2022】037 号),由中国电…...
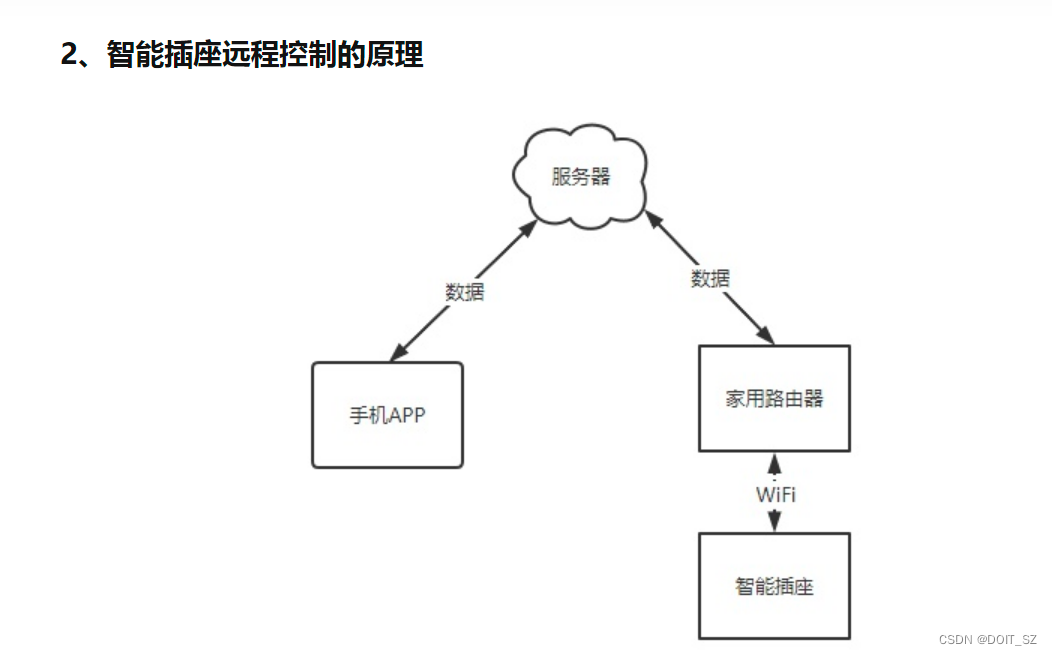
智能家居Homekit系列一智能插座
WiFi智能插座对于新手接触智能家居产品更加友好,不需要额外购买网关设备 很多智能小配件也给我们得生活带来极大的便捷,智能插座就是其中之一,比如外出忘记关空调,可以拿起手机远程关闭。 简单说就是:插座可以连接wi…...

React(三):脚手架、组件化、生命周期、父子组件通信、插槽
React(三)一、脚手架安装和创建1.安装脚手架2.创建脚手架3.看看脚手架目录4.运行脚手架二、脚手架下从0开始写代码三、组件化1.类组件2.函数组件四、React的生命周期1.认识生命周期2.图解生命周期(1)Constructor(2&…...

UE5 学习系列(二)用户操作界面及介绍
这篇博客是 UE5 学习系列博客的第二篇,在第一篇的基础上展开这篇内容。博客参考的 B 站视频资料和第一篇的链接如下: 【Note】:如果你已经完成安装等操作,可以只执行第一篇博客中 2. 新建一个空白游戏项目 章节操作,重…...

简易版抽奖活动的设计技术方案
1.前言 本技术方案旨在设计一套完整且可靠的抽奖活动逻辑,确保抽奖活动能够公平、公正、公开地进行,同时满足高并发访问、数据安全存储与高效处理等需求,为用户提供流畅的抽奖体验,助力业务顺利开展。本方案将涵盖抽奖活动的整体架构设计、核心流程逻辑、关键功能实现以及…...

Vue3 + Element Plus + TypeScript中el-transfer穿梭框组件使用详解及示例
使用详解 Element Plus 的 el-transfer 组件是一个强大的穿梭框组件,常用于在两个集合之间进行数据转移,如权限分配、数据选择等场景。下面我将详细介绍其用法并提供一个完整示例。 核心特性与用法 基本属性 v-model:绑定右侧列表的值&…...

蓝桥杯 2024 15届国赛 A组 儿童节快乐
P10576 [蓝桥杯 2024 国 A] 儿童节快乐 题目描述 五彩斑斓的气球在蓝天下悠然飘荡,轻快的音乐在耳边持续回荡,小朋友们手牵着手一同畅快欢笑。在这样一片安乐祥和的氛围下,六一来了。 今天是六一儿童节,小蓝老师为了让大家在节…...

Matlab | matlab常用命令总结
常用命令 一、 基础操作与环境二、 矩阵与数组操作(核心)三、 绘图与可视化四、 编程与控制流五、 符号计算 (Symbolic Math Toolbox)六、 文件与数据 I/O七、 常用函数类别重要提示这是一份 MATLAB 常用命令和功能的总结,涵盖了基础操作、矩阵运算、绘图、编程和文件处理等…...

Caliper 配置文件解析:config.yaml
Caliper 是一个区块链性能基准测试工具,用于评估不同区块链平台的性能。下面我将详细解释你提供的 fisco-bcos.json 文件结构,并说明它与 config.yaml 文件的关系。 fisco-bcos.json 文件解析 这个文件是针对 FISCO-BCOS 区块链网络的 Caliper 配置文件,主要包含以下几个部…...

视频行为标注工具BehaviLabel(源码+使用介绍+Windows.Exe版本)
前言: 最近在做行为检测相关的模型,用的是时空图卷积网络(STGCN),但原有kinetic-400数据集数据质量较低,需要进行细粒度的标注,同时粗略搜了下已有开源工具基本都集中于图像分割这块,…...

SQL慢可能是触发了ring buffer
简介 最近在进行 postgresql 性能排查的时候,发现 PG 在某一个时间并行执行的 SQL 变得特别慢。最后通过监控监观察到并行发起得时间 buffers_alloc 就急速上升,且低水位伴随在整个慢 SQL,一直是 buferIO 的等待事件,此时也没有其他会话的争抢。SQL 虽然不是高效 SQL ,但…...

【无标题】路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论
路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论 一、传统路径模型的根本缺陷 在经典正方形路径问题中(图1): mermaid graph LR A((A)) --- B((B)) B --- C((C)) C --- D((D)) D --- A A -.- C[无直接路径] B -…...

从“安全密码”到测试体系:Gitee Test 赋能关键领域软件质量保障
关键领域软件测试的"安全密码":Gitee Test如何破解行业痛点 在数字化浪潮席卷全球的今天,软件系统已成为国家关键领域的"神经中枢"。从国防军工到能源电力,从金融交易到交通管控,这些关乎国计民生的关键领域…...
