【汉诺塔 —— (经典分治递归)】
汉诺塔 —— (经典分治递归)
- 一.汉诺塔介绍
- 二.分治算法解决汉诺塔问题
- 三.汉诺塔问题的代码实现
- 四.主函数测试展示
一.汉诺塔介绍
汉诺塔问题源自印度一个古老的传说,印度教的“创造之神”梵天创造世界时做了 3 根金刚石柱,其中的一根柱子上按照从小到大的顺序摞着 64 个黄金圆盘。梵天命令一个叫婆罗门的门徒将所有的圆盘移动到另一个柱子上,移动过程中必须遵守以下规则:
每次只能移动柱子最顶端的一个圆盘;
每个柱子上,小圆盘永远要位于大圆盘之上;
图 1 给您展示了包含 3 个圆盘的汉诺塔问题:
图 1 汉诺塔问题
一根柱子上摞着 3 个不同大小的圆盘,那么在不违反规则的前提下,如何将它们移动到另一个柱子上呢?图 2 给大家提供了一种实现方案:
图 2 汉诺塔问题的解决方案
汉诺塔问题中,3 个圆盘至少需要移动 7 次,移动 n 的圆盘至少需要操作 2n-1 次。
在汉诺塔问题中,当圆盘个数不大于 3 时,多数人都可以轻松想到移动方案,随着圆盘数量的增多,汉诺塔问题会越来越难。也就是说,圆盘的个数直接决定了汉诺塔问题的难度,解决这样的问题可以尝试用分治算法,将移动多个圆盘的问题分解成多个移动少量圆盘的小问题,这些小问题很容易解决,从而可以找到整个问题的解决方案。
二.分治算法解决汉诺塔问题
为了方便讲解,我们将 3 个柱子分别命名为起始柱、目标柱和辅助柱。实际上,解决汉诺塔问题是有规律可循的:
1) 当起始柱上只有 1 个圆盘时,我们可以很轻易地将它移动到目标柱上;
2) 当起始柱上有 2 个圆盘时,移动过程如下图所示:
图 3 移动两个圆盘
移动过程是:先将起始柱上的 1 个圆盘移动到辅助柱上,然后将起始柱上遗留的圆盘移动到目标柱上,最后将辅助柱上的圆盘移动到目标柱上。
3) 当起始柱上有 3 个圆盘时,移动过程如图 2 所示,仔细观察会发现,移动过程和 2 个圆盘的情况类似:先将起始柱上的 2 个圆盘移动到辅助柱上,然后将起始柱上遗留的圆盘移动到目标柱上,最后将辅助柱上的圆盘移动到目标柱上。
通过分析以上 3 种情况的移动思路,可以总结出一个规律:对于 n 个圆盘的汉诺塔问题,移动圆盘的过程是:
1.将起始柱上的 n-1 个圆盘移动到辅助柱上;
2.将起始柱上遗留的 1 个圆盘移动到目标柱上;
3.将辅助柱上的所有圆盘移动到目标柱上。
由此,n 个圆盘的汉诺塔问题就简化成了 n-1 个圆盘的汉诺塔问题。按照同样的思路,n-1 个圆盘的汉诺塔问题还可以继续简化,直至简化为移动 3 个甚至更少圆盘的汉诺塔问题。
三.汉诺塔问题的代码实现
//将n个圆盘借助by从from移到to
void hanoi(int n, char from, char to, char by)
{void move(int n, char x, char y);if (n == 1)move(n, from, to);else{hanoi(n - 1, from, by, to);move(n, from, to);hanoi(n - 1, by, to, from);}
}void move(int n, char x, char y)
{printf("第%d个圆盘从%c->%c\n", n, x, y);
}int main() {int n = 0;printf("请输入A柱上圆盘个数:");scanf("%d", &n);//将n个圆盘借助C从A移到Bprintf("移动方法展示:\n");hanoi(n, 'A', 'B', 'C');return 0;
}
四.主函数测试展示


相关文章:

【汉诺塔 —— (经典分治递归)】
汉诺塔 —— (经典分治递归) 一.汉诺塔介绍二.分治算法解决汉诺塔问题三.汉诺塔问题的代码实现四.主函数测试展示 一.汉诺塔介绍 汉诺塔问题源自印度一个古老的传说,印度教的“创造之神”梵天创造世界时做了 3 根金刚石柱,其中的一…...

APP运营常用的ChatGPT通用提示词模板
用户获取:请帮助我制定一个用户获取计划,包括目标用户群体、获取渠道、营销策略等方面的内容。 用户留存:我们希望提高用户的留存率,请帮助我分析用户流失的原因,并提供一些留存策略和措施。 用户活跃度:…...
医学检验(LIS)管理系统源码,LIS源码,云LIS系统源码
医学检验(LIS)管理系统源码,云LIS系统全套商业源码 随着全自动生化分析仪、全自动免疫分析仪和全自动血球计数器等仪器的使用,检验科的大多数项目实现了全自动化分析。全自动化分析引入后,组合化验增多,更好的满足了临床需要&…...
RabbitMQ 安装(在docker容器中安装)
为什么要用? RabbitMQ是一个开源的消息代理和队列服务器,主要用于在不同的应用程序之间传递消息。它实现了高级消息队列协议(AMQP),并提供了一种异步协作机制,以帮助提高系统的性能和扩展性。 RabbitMQ的作…...

机器学习入门
简介 https://huggingface.co/是一个AI社区,类似于github的地位。它开源了许多机器学习需要的基础组件如:Transformers, Tokenizers等。 许多公司也在不断地往上面提交新的模型和数据集,利用它你可以获取以下内容: Datasets : 数…...
HarmonyOS ArkTS 保存应用数据(十)
1 概述 在移动互联网蓬勃发展的今天,移动应用给我们生活带来了极大的便利,这些便利的本质在于数据的互联互通。因此在应用的开发中数据存储占据了非常重要的位置,HarmonyOS应用开发也不例外。 2 什么是首选项 首选项为应用提供Key-Value键…...

【JavaEE】Spring更简单的存储和获取对象(类注解、方法注解、属性注入、Setter注入、构造方法注入)
一、存储Bean对象 在这篇文章中我介绍了Spring最简单的创建和使用:Spring的创建和使用 其中存储Bean对象是这样的: 1.1 配置扫描路径 想要成功把对象存到Spring中,我们需要配置对象的扫描包路径 这样的话,就只有被配置了的包…...
linux上的通用拍照程序
最近因为工作需要,在ubuntu上开发了一个拍照程序。 为了找到合适的功能研究了好几种实现方式,在这里记录一下。 目录 太长不看版 探索过程 v4l2 QT opencv4.2 打开摄像头 为什么不直接打开第一个视频节点 获取所有分辨率 切换摄像头 太长不看…...

代码随想录-刷题第七天
454. 四数相加II 题目链接:454. 四数相加II 思路:哈希法。使用map集合,key存放ab的值,value存放ab出现的次数。使用两层循环,循环前两个数组,找出ab,对map赋值。再用两层循环,遍历…...

C# 获取图像、字体等对象大小的数据结构SizeF
如果你想要获取字符串 "你好吗" 的字节数组长度或者字符数, 使用如下代码: string s "你好吗"; //字节数组长度 int byteCount System.Text.Encoding.UTF8.GetBytes(s).Length; //字符数 int charCount s.Length; 如果你想获取…...
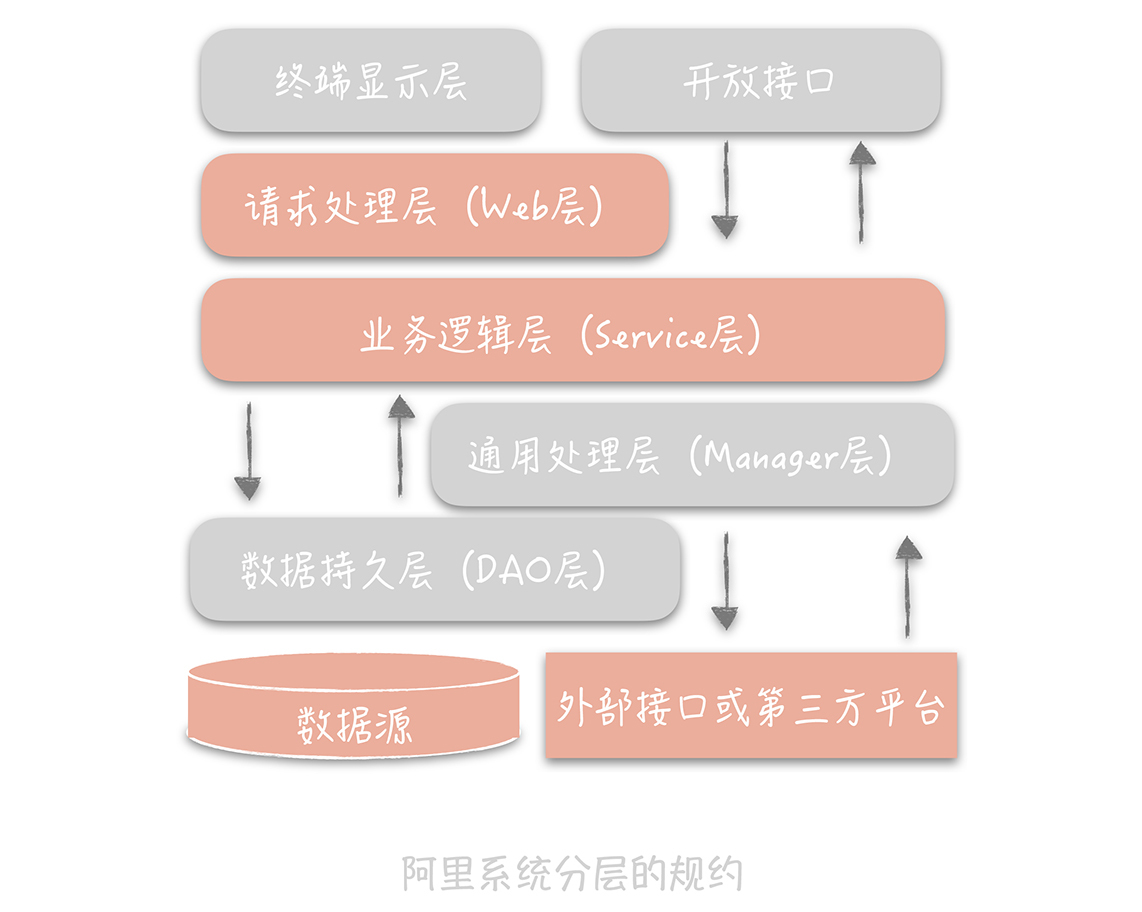
「 系统设计 」 为什么要做架构分层?
「 系统设计 」 为什么要做架构分层? 参考&鸣谢 3.设计模式之分层思维:为什么要做代码分层架构? 从零开始学架构(八)分层架构和设计模式 架构模式之分层架构总结 文章目录 「 系统设计 」 为什么要做架构分层&…...
)
4:kotlin 方法(Functions)
想要声明一个函数需要使用fun关键字 fun hello() {return println("Hello, world!") }fun main() {hello()// Hello, world! }格式: fun 方法名(参数1: 参数1类型, 参数2 : 参数2类型, ...): 返回值类型 {方法体return 返回值 }fun 方法名(参数1: 参数1类型, 参数2…...

Pycharm run 输出界面控制一行能够输出的元素个数
Pycharm run 输出界面控制一行能够输出的元素个数 今天遇到了一个问题,当我们在 Pycharm 中打印输出数组时,如果数组一行的元素个数过多,那么我们在打印时就会出现以下问题。 代码如下: import numpy as npx np.array([[0., 0.7…...
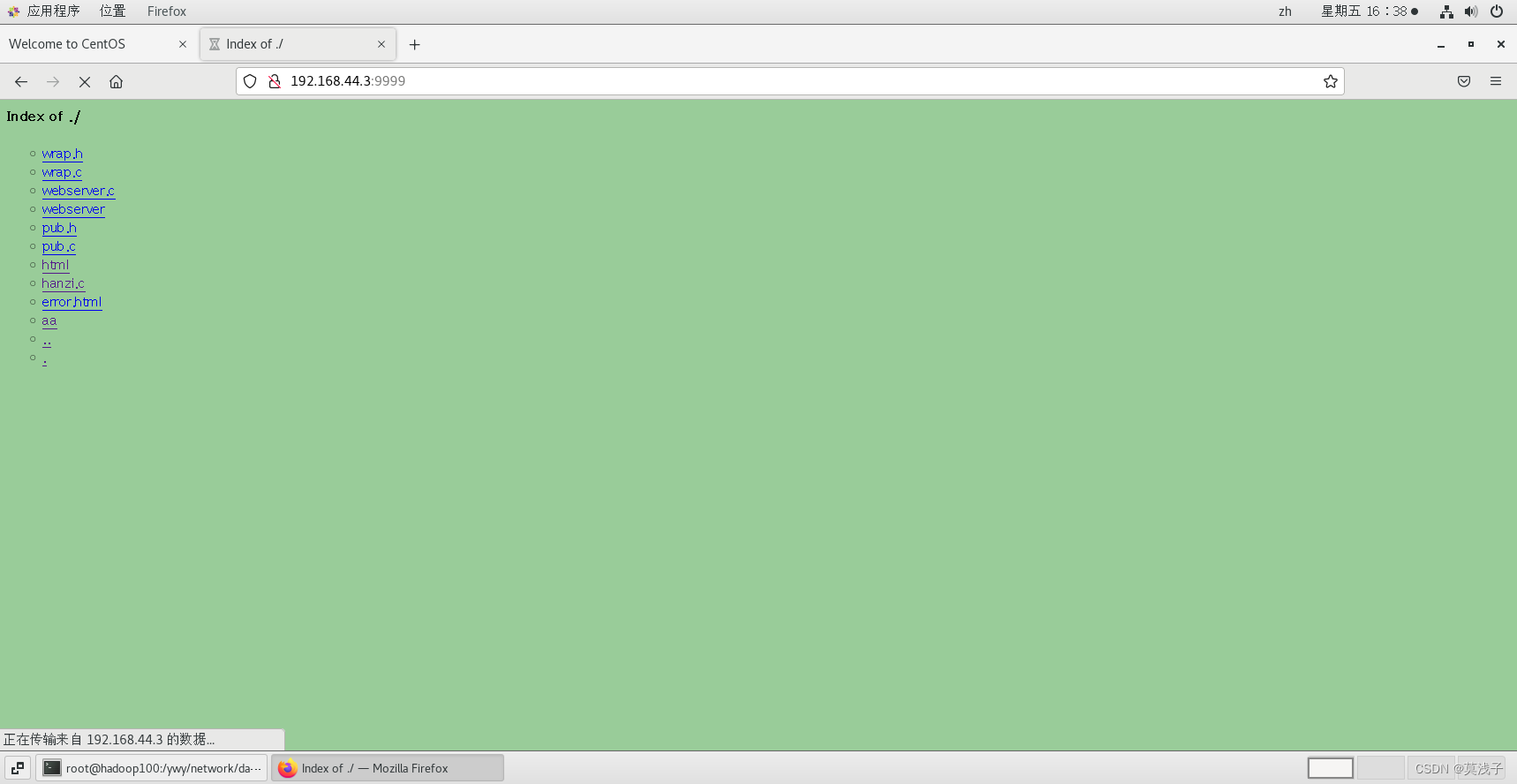
C++初级项目webserver项目流程介绍(2)
一、引言 C的webserver项目是自己在学完网络编程后根据网课的内容做的一个初级的网络编程项目。 这个项目的效果是可以在浏览器通过输入网络IP地址和端口,然后打开对应的文件目录 效果如下: 也可以打开文件夹后点击目录,打开到对应的文件夹…...

SIPp mac和debian用法可能略有差别
<ereg regexp"<(.*)>" search_in"hdr" header"Contact:" check_it"true" assign_to"dummy,remote_contact"/> debian没事,但mac报错 <变< >变> 就都冇问题了 https://github.…...

echarts的横向柱状图文字省略,鼠标移入显示内容 vue3
效果图 文字省略 提示 如果是在x轴上的,就在x轴上添加triggerEvent: true,如果是y轴就在y轴添加,我是在y轴上添加的 并且自定义的方法(我取名为extension) // echarts 横向省略文字 鼠标移入显示内容 export const extension…...
laravel8安装多应用多模块(笔记三)
先安装laravel8 Laravel 安装(笔记一)-CSDN博客 一、进入项目根目录安装 laravel-modules composer require nwidart/laravel-modules 二、 大于laravel5需配置provider,自动生成配置文件 php artisan vendor:publish --provider"Nwid…...
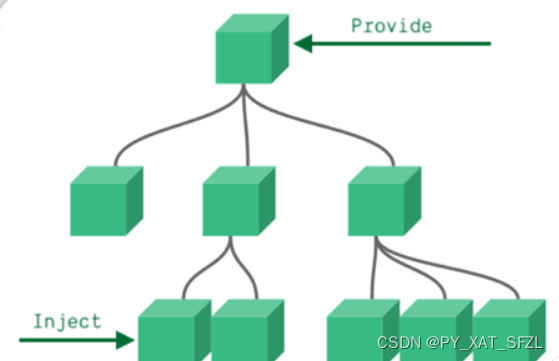
Vue组件的几种通信方式
这里写目录标题 Vue组件的几种通信(数据传递)方式非父子组件间通信(Bus事件总线)介绍实例 非父子通信-provide&inject1.作用2.场景3.语法4.注意 父子组件间的通信固定props属性名(v-model)介绍实例 不固…...
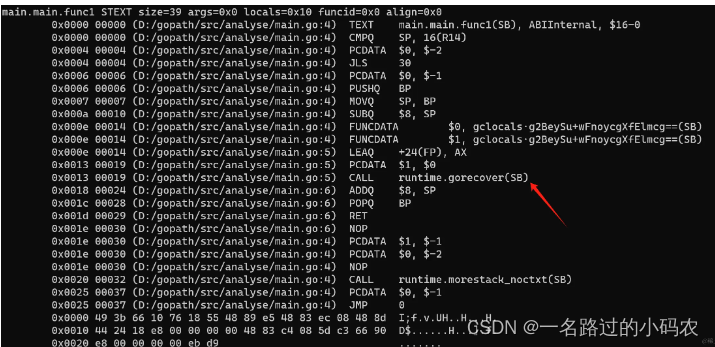
golang panic关键词执行原理与代码分析
使用的go版本为 go1.21.2 首先我们写一个简单的panic调度与捕获代码 package mainfunc main() {defer func() {recover()}()panic("panic test") }通过go build -gcflags -S main.go获取到对应的汇编代码 可以看到当我们调度panic时,Go的编译器会将这段…...
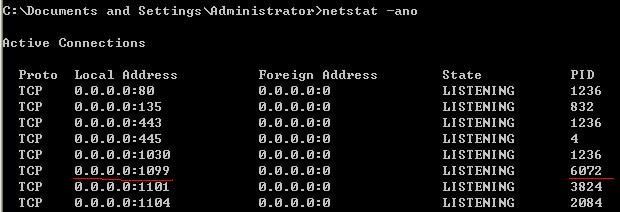
Error running Tomcat8: Address localhost:1099 is already in use 错误解决
摘要: 有时候运行web项目的时候会遇到 Error running Tomcat8: Address localhost:1099 is already in use 的错误,导致web项目无法运行。这篇 blog 介绍了解决办法。 有时候运行web项目的时候会遇到 Error running Tomcat8: Address localhost:1099 is already in …...

Android Wi-Fi 连接失败日志分析
1. Android wifi 关键日志总结 (1) Wi-Fi 断开 (CTRL-EVENT-DISCONNECTED reason3) 日志相关部分: 06-05 10:48:40.987 943 943 I wpa_supplicant: wlan0: CTRL-EVENT-DISCONNECTED bssid44:9b:c1:57:a8:90 reason3 locally_generated1解析: CTR…...

<6>-MySQL表的增删查改
目录 一,create(创建表) 二,retrieve(查询表) 1,select列 2,where条件 三,update(更新表) 四,delete(删除表…...

关于nvm与node.js
1 安装nvm 安装过程中手动修改 nvm的安装路径, 以及修改 通过nvm安装node后正在使用的node的存放目录【这句话可能难以理解,但接着往下看你就了然了】 2 修改nvm中settings.txt文件配置 nvm安装成功后,通常在该文件中会出现以下配置&…...

iPhone密码忘记了办?iPhoneUnlocker,iPhone解锁工具Aiseesoft iPhone Unlocker 高级注册版分享
平时用 iPhone 的时候,难免会碰到解锁的麻烦事。比如密码忘了、人脸识别 / 指纹识别突然不灵,或者买了二手 iPhone 却被原来的 iCloud 账号锁住,这时候就需要靠谱的解锁工具来帮忙了。Aiseesoft iPhone Unlocker 就是专门解决这些问题的软件&…...

渗透实战PortSwigger靶场-XSS Lab 14:大多数标签和属性被阻止
<script>标签被拦截 我们需要把全部可用的 tag 和 event 进行暴力破解 XSS cheat sheet: https://portswigger.net/web-security/cross-site-scripting/cheat-sheet 通过爆破发现body可以用 再把全部 events 放进去爆破 这些 event 全部可用 <body onres…...

1.3 VSCode安装与环境配置
进入网址Visual Studio Code - Code Editing. Redefined下载.deb文件,然后打开终端,进入下载文件夹,键入命令 sudo dpkg -i code_1.100.3-1748872405_amd64.deb 在终端键入命令code即启动vscode 需要安装插件列表 1.Chinese简化 2.ros …...

HBuilderX安装(uni-app和小程序开发)
下载HBuilderX 访问官方网站:https://www.dcloud.io/hbuilderx.html 根据您的操作系统选择合适版本: Windows版(推荐下载标准版) Windows系统安装步骤 运行安装程序: 双击下载的.exe安装文件 如果出现安全提示&…...

动态 Web 开发技术入门篇
一、HTTP 协议核心 1.1 HTTP 基础 协议全称 :HyperText Transfer Protocol(超文本传输协议) 默认端口 :HTTP 使用 80 端口,HTTPS 使用 443 端口。 请求方法 : GET :用于获取资源,…...

关于uniapp展示PDF的解决方案
在 UniApp 的 H5 环境中使用 pdf-vue3 组件可以实现完整的 PDF 预览功能。以下是详细实现步骤和注意事项: 一、安装依赖 安装 pdf-vue3 和 PDF.js 核心库: npm install pdf-vue3 pdfjs-dist二、基本使用示例 <template><view class"con…...

MySQL的pymysql操作
本章是MySQL的最后一章,MySQL到此完结,下一站Hadoop!!! 这章很简单,完整代码在最后,详细讲解之前python课程里面也有,感兴趣的可以往前找一下 一、查询操作 我们需要打开pycharm …...



