XTU OJ 1146 矩阵乘法学习笔记
原题
题目描述
给你两个矩阵A(n*k),B(k*m),请求A*B。
输入
第一行是一个整数K,表示样例的个数。 每个样例包含两个矩阵A和B。 每个矩阵的第一行是两个整数n,m,(1≤n,m≤10)表示矩阵的行和列 以后的n行,每行m个整数,每个整数的绝对值不超过100。输入保证A和B是可乘的。
输出
输出每个样例的结果矩阵,矩阵的整数之间用一个空格隔开,行尾无空格。
样例输入
2 2 2 1 1 1 1 2 1 1 1 2 2 1 1 1 1 2 2 1 1 1 0
样例输出
2 2 2 1 2 1
原题链接
传送门
代码
#include<bits/stdc++.h>
using namespace std;const int N=20;
int a[N][N],b[N][N],c[N][N];int main()
{int t;scanf("%d",&t);while(t--){int n,k,l,m;scanf("%d%d",&n,&k);for(int i=0;i<n;i++){for(int j=0;j<k;j++){scanf("%d",&a[i][j]);}}scanf("%d%d",&l,&m);for(int i=0;i<l;i++){for(int j=0;j<m;j++){scanf("%d",&b[i][j]);}}for(int i=0;i<n;i++){for(int j=0;j<m;j++){c[i][j]=0;for(int h=0;h<k;h++){c[i][j]+=a[i][h]*b[h][j];}printf("%d",c[i][j]);if(j!=m-1) printf(" ");}printf("\n");}}return 0;
}总结
1.矩阵乘法是啥对我来说可能是这道题最大的难点,矩阵乘法,简单来说,给定两个矩阵,第一个矩阵的列数和第二个矩阵的行数相等,两个矩阵相乘的结果是,一个新的矩阵,新的矩阵行数和第一个矩阵相等,列数和第二个矩阵相等,比如一个2行3列的矩阵,乘以一个3行2列的矩阵,答案是一个2行2列的矩阵,答案矩阵的第一行第一个元素是,第一个矩阵第一行的所有元素和第二个矩阵第一列的所有元素逐项相乘并求和,答案矩阵第一行第二个元素是,第一个矩阵第一行所有元素和第二个矩阵第二列所有元素逐项相乘并求和
2.题目保证了第一个矩阵的列数等于第二个矩阵的行数
3.行尾没有空格,注意判断每一行最后一个元素的数组下标
4.每一次使用c数组都需要初始化,防止前一次循环对当前循环产生影响
5.(有时候感觉一摸一样的代码难以ac,重新敲一遍可以通过,算是一个魔咒还是因为啥原原因……)
相关文章:

XTU OJ 1146 矩阵乘法学习笔记
原题 题目描述 给你两个矩阵A(n*k),B(k*m),请求A*B。 输入 第一行是一个整数K,表示样例的个数。 每个样例包含两个矩阵A和B。 每个矩阵的第一行是两个整数n,m,(1≤n,m≤10)表示矩阵的行和列 以后的n行,每行m个整数,每个整数的绝对值不超过…...
基于官方YOLOv4开发构建目标检测模型超详细实战教程【以自建缺陷检测数据集为例】
本文是关于基于YOLOv4开发构建目标检测模型的超详细实战教程,超详细实战教程相关的博文在前文有相应的系列,感兴趣的话可以自行移步阅读即可:《基于yolov7开发实践实例分割模型超详细教程》 《YOLOv7基于自己的数据集从零构建模型完整训练、…...

1、Docker概述与安装
相关资源网站: ● docker官网:http://www.docker.com ● Docker Hub仓库官网: https://hub.docker.com/ 注意,如果只是想看Docker的安装,可以直接往下拉跳转到Docker架构与安装章节下的Docker具体安装步骤,一步步带你安…...

论文笔记——FasterNet
为了设计快速神经网络,许多工作都集中在减少浮点运算(FLOPs)的数量上。然而,作者观察到FLOPs的这种减少不一定会带来延迟的类似程度的减少。这主要源于每秒低浮点运算(FLOPS)效率低下。 为了实现更快的网络,作者重新回顾了FLOPs的运算符,并证明了如此低的FLOPS主要是由…...

计算机组成原理-固态硬盘SSD
文章目录 总览机械硬盘vs固态硬盘固态硬盘的结构固态硬盘与机械硬盘相比的特点磨损均衡技术例题 总览 机械硬盘vs固态硬盘 固态硬盘采用闪存技术,是电可擦除ROM 下图右边黑色的块块就是一块一块的闪存芯片 固态硬盘的结构 块大小16KB~512KB 页大小512B~4KB 对固…...
Electron+VUE3开发简版的编辑器【文件预览】
简版编辑器的功能主要是: 打开对话框,选择文件后台读取文件文件前端展示文件内容。主要技术栈是VUE3、Electron和Nodejs,VUE3做页面交互,Electron提供一个可执行Nodejs的环境以及支撑整个应用的环境,nodeJS负责读取文件内容。 环境配置、安装依赖这些步骤就不再叙述了。 …...
docker、elasticsearch8、springboot3集成备忘
目录 一、背景 二、安装docker 三、下载安装elasticsearch 四、下载安装elasticsearch-head 五、springboot集成elasticsearch 一、背景 前两年研究了一段时间elasticsearch,当时也是网上找了很多资料,最后解决个各种问题可以在springboot上运行了…...

【Lombok使用详解】
目录 前言:注解速查1.Lombok概念2.安装Lombok3. 使用Lombok3.1 😊Data3.2 GetterSetter3.3 NonNull3.4 Synchronized3.5 ToString:自动生成toString()方法3.6 Cleanup3.7 EqualsAndHashCode 前言:注解速查 NonNull : 用在成员方法…...

Tars框架 Tars-Go 学习
Tars 框架安装 网上安装教程比较多,官方可以参数这个 TARS官方文档 (tarsyun.com) 本文主要介绍部署应用。 安装完成后Tars 界面 增加应用amc 部署申请 amc.GoTestServer.GoTestObj 名称不知道的可以参考自己创建的app config 点击刷新可以看到自己部署的应用 服…...
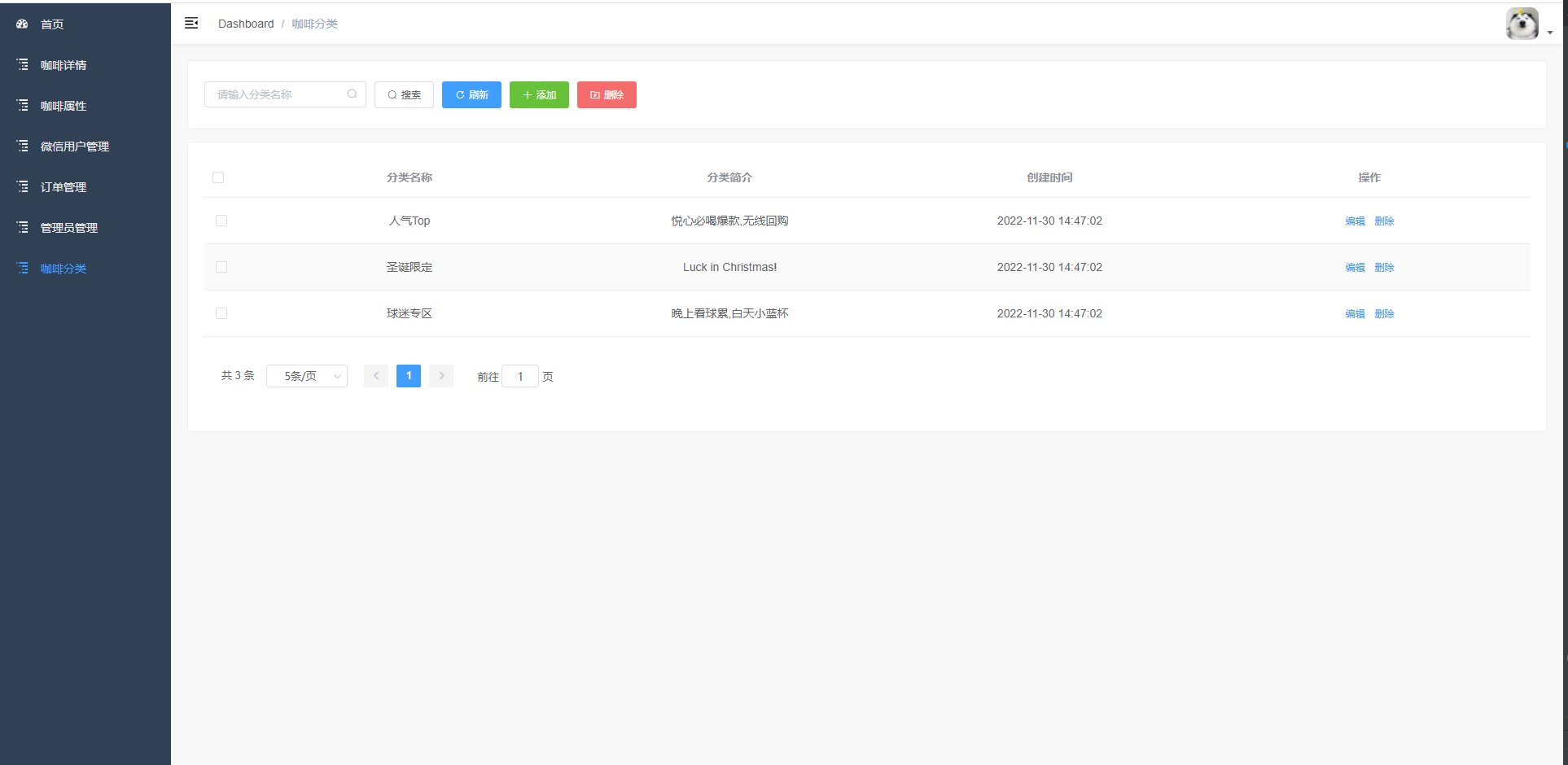
基于JAVA+SpringBoot+VUE+微信小程序的前后端分离咖啡小程序
✌全网粉丝20W,csdn特邀作者、博客专家、CSDN新星计划导师、java领域优质创作者,博客之星、掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域和毕业项目实战✌ 🍅文末获取项目下载方式🍅 一、项目背景介绍: 随着社会的快速发展和…...

2015年全国硕士研究生入学统一考试管理类专业学位联考数学试题——解析版
文章目录 2015 级考研管理类联考数学真题一、问题求解(本大题共 15 小题,每小题 3 分,共 45 分)下列每题给出 5 个选项中,只有一个是符合要求的,请在答题卡上将所选择的字母涂黑。真题(2015-01&…...

优秀软件设计特征与原则
1.摘要 一款软件产品好不好用, 除了拥有丰富的功能和人性化的界面设计之外, 还有其深厚的底层基础, 而设计模式和算法是构建这个底层基础的基石。好的设计模式能够让产品开发快速迭代且稳定可靠, 迅速抢占市场先机;而好的算法能够让产品具有核心价值, 例如字节跳动…...

设备管理系统-设备管理软件
一、为什么要使用设备管理系统 1.企业扩张快,设备配置多,管理混乱。 2.设备数量多,存放地点多,查找麻烦。 3.同类设备单独管理, 困难。 4.设备较多时相关信息统计容易出错,错误后修改困难。 二、凡尔码设备管理软件的…...

物联网AI MicroPython学习之语法 I2S音频总线接口
学物联网,来万物简单IoT物联网!! I2S 介绍 模块功能: I2S音频总线驱动模块 接口说明 I2S - 构建I2S对象 函数原型:I2S(id, sck, ws, sd, mode, bits, format, rate, ibuf)参数说明: 参数类型必选参数?…...

Day31| Leetcode 455. 分发饼干 Leetcode 376. 摆动序列 Leetcode 53. 最大子数组和
进入贪心了,我觉得本专题是最烧脑的专题 Leetcode 455. 分发饼干 题目链接 455 分发饼干 让大的饼干去满足需求量大的孩子即是本题的思路: class Solution { public:int findContentChildren(vector<int>& g, vector<int>& s) {…...
基于C#实现赫夫曼树
赫夫曼树又称最优二叉树,也就是带权路径最短的树,对于赫夫曼树,我想大家对它是非常的熟悉,也知道它的应用场景,但是有没有自己亲手写过,这个我就不清楚了,不管以前写没写,这一篇我们…...

Android 13.0 app进程保活白名单功能实现
1.前言 在13.0的系统rom产品开发中,在某些重要的app即使进入后台,产品需求要求也不想被系统杀掉进程,需要app长时间保活,就是app进程保活白名单功能的实现, 所以需要在系统杀进程的时候不杀掉白名单的进程,接下来就看怎么样来实现这些功能 2.app进程保活白名单功能实…...

查找学习笔记
1、静态查找表 以下查找的索引均从1开始 (1)顺序查找(带哨兵) #include<iostream> #include<vector>using namespace std;int search(vector<int> arr, int key) {arr[0] key;int i;for (i arr.size() - 1…...

Qt QIODevice介绍
作者:令狐掌门 技术交流QQ群:675120140 csdn博客:https://mingshiqiang.blog.csdn.net/ 文章目录 主要功能用法示例读取数据写入数据使用数据流基于套接字的读写注意事项QIODevice 是 Qt 中所有输入/输出设备的抽象基类。它为派生类提供了一组标准的接口用于读写数据。这些派…...
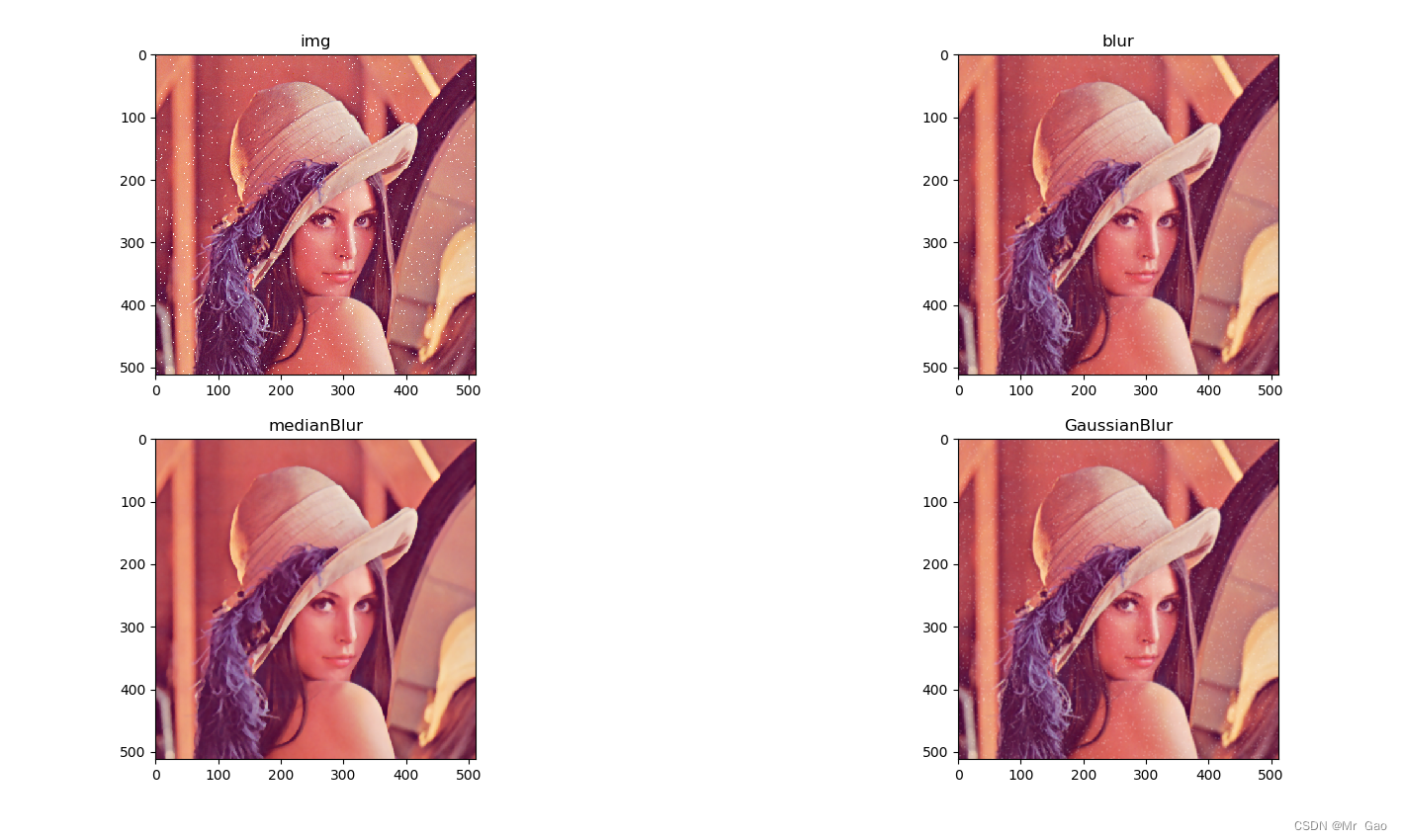
python -opencv 中值滤波 ,均值滤波,高斯滤波实战
python -opencv 中值滤波 ,均值滤波,高斯滤波实战 cv2.blur-均值滤波 cv2.medianBlur-中值滤波 cv2.GaussianBlur-高斯滤波 直接看代码吧,代码很简单: import copy import math import matplotlib.pyplot as plt import matp…...

铭豹扩展坞 USB转网口 突然无法识别解决方法
当 USB 转网口扩展坞在一台笔记本上无法识别,但在其他电脑上正常工作时,问题通常出在笔记本自身或其与扩展坞的兼容性上。以下是系统化的定位思路和排查步骤,帮助你快速找到故障原因: 背景: 一个M-pard(铭豹)扩展坞的网卡突然无法识别了,扩展出来的三个USB接口正常。…...

测试微信模版消息推送
进入“开发接口管理”--“公众平台测试账号”,无需申请公众账号、可在测试账号中体验并测试微信公众平台所有高级接口。 获取access_token: 自定义模版消息: 关注测试号:扫二维码关注测试号。 发送模版消息: import requests da…...

OpenLayers 可视化之热力图
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 热力图(Heatmap)又叫热点图,是一种通过特殊高亮显示事物密度分布、变化趋势的数据可视化技术。采用颜色的深浅来显示…...

Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以?
Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以? 在 Golang 的面试中,map 类型的使用是一个常见的考点,其中对 key 类型的合法性 是一道常被提及的基础却很容易被忽视的问题。本文将带你深入理解 Golang 中…...

Qt Http Server模块功能及架构
Qt Http Server 是 Qt 6.0 中引入的一个新模块,它提供了一个轻量级的 HTTP 服务器实现,主要用于构建基于 HTTP 的应用程序和服务。 功能介绍: 主要功能 HTTP服务器功能: 支持 HTTP/1.1 协议 简单的请求/响应处理模型 支持 GET…...

从零开始打造 OpenSTLinux 6.6 Yocto 系统(基于STM32CubeMX)(九)
设备树移植 和uboot设备树修改的内容同步到kernel将设备树stm32mp157d-stm32mp157daa1-mx.dts复制到内核源码目录下 源码修改及编译 修改arch/arm/boot/dts/st/Makefile,新增设备树编译 stm32mp157f-ev1-m4-examples.dtb \stm32mp157d-stm32mp157daa1-mx.dtb修改…...

ElasticSearch搜索引擎之倒排索引及其底层算法
文章目录 一、搜索引擎1、什么是搜索引擎?2、搜索引擎的分类3、常用的搜索引擎4、搜索引擎的特点二、倒排索引1、简介2、为什么倒排索引不用B+树1.创建时间长,文件大。2.其次,树深,IO次数可怕。3.索引可能会失效。4.精准度差。三. 倒排索引四、算法1、Term Index的算法2、 …...

实现弹窗随键盘上移居中
实现弹窗随键盘上移的核心思路 在Android中,可以通过监听键盘的显示和隐藏事件,动态调整弹窗的位置。关键点在于获取键盘高度,并计算剩余屏幕空间以重新定位弹窗。 // 在Activity或Fragment中设置键盘监听 val rootView findViewById<V…...

如何在最短时间内提升打ctf(web)的水平?
刚刚刷完2遍 bugku 的 web 题,前来答题。 每个人对刷题理解是不同,有的人是看了writeup就等于刷了,有的人是收藏了writeup就等于刷了,有的人是跟着writeup做了一遍就等于刷了,还有的人是独立思考做了一遍就等于刷了。…...

Device Mapper 机制
Device Mapper 机制详解 Device Mapper(简称 DM)是 Linux 内核中的一套通用块设备映射框架,为 LVM、加密磁盘、RAID 等提供底层支持。本文将详细介绍 Device Mapper 的原理、实现、内核配置、常用工具、操作测试流程,并配以详细的…...
