多智能体集群协同控制笔记(1):线性无领航多智能体系统的一致性
对于连续时间高阶线性多智能体系统的状态方程为:
x˙i(t)=Axi(t)+Bui(t),i=1,2..N\dot {\mathbf{x}}_i(t)=A\mathbf{x}_i(t)+B\mathbf{u}_i(t),i=1,2..N x˙i(t)=Axi(t)+Bui(t),i=1,2..N
下标iii代表第iii个智能体,ui(t)∈Rq×1\mathbf{u}_i(t)\in R^{q \times 1}ui(t)∈Rq×1表示第iii个智能体的控制输入变量,xi(t)∈Rp×1\mathbf{x}_i(t)\in R^{p \times 1}xi(t)∈Rp×1表示第iii个智能体的状态变量。系统的一致性即设计控制器ui(t)\mathbf{u}_i(t)ui(t)保证如下等式成立:
limt→∞x1(t)=limt→∞x2(t)=...=limt→∞xN(t)\lim_{t\rightarrow\infty}\mathbf{x}_1(t)=\lim_{t\rightarrow\infty}\mathbf{x}_2(t)=...=\lim_{t\rightarrow\infty}\mathbf{x}_N(t) t→∞limx1(t)=t→∞limx2(t)=...=t→∞limxN(t)
-
定义Laplacian矩阵L={lij}i,j=1,..NL=\{l_{ij}\}_{i,j=1,..N}L={lij}i,j=1,..N,其中:
lij={∑j=1,j≠iNaiji=j−aiji≠jl_{ij}=\begin{cases} \sum_{j=1,j\ne i}^Na_{ij} & i = j\\ -a_{ij}& i\ne j \end{cases} lij={∑j=1,j=iNaij−aiji=ji=j -
定义变量:ξi(t)=∑j=1Naij(xi(t)−xj(t))\mathbf{\xi}_i(t)=\sum_{j=1}^Na_{ij}(\mathbf{x}_i(t)-\mathbf{x}_j(t))ξi(t)=∑j=1Naij(xi(t)−xj(t)),定义:
ξ(t)=(L⊗Ip)X(t)\mathbf{\xi}(t)=(L\otimes I_p)X(t) ξ(t)=(L⊗Ip)X(t)
其中:X(t)=[x1T(t),x2T(t),..xNT(t)]TX(t)=[\mathbf{x}_1^T(t),\mathbf{x}_2^T(t),..\mathbf{x}_N^T(t)]^TX(t)=[x1T(t),x2T(t),..xNT(t)]T,ξ(t)=[ξ1(t)T,ξ2(t)T,..ξN(t)T]T\mathbf{\xi}(t)=[\mathbf{\xi}_1(t)^T,\mathbf{\xi}_2(t)^T,..\mathbf{\xi}_N(t)^T]^Tξ(t)=[ξ1(t)T,ξ2(t)T,..ξN(t)T]T; -
定义控制器:ui(t)=cK1ξi(t)\mathbf{u}_i(t)=cK_1\mathbf{\xi}_i(t)ui(t)=cK1ξi(t),总的控制策略为:
u(t)=(IN⊗cK1)ξ(t)=(IN⊗cK1)(L⊗Ip)X(t)\mathbf{u}(t)=(I_N\otimes cK_1)\mathbf{\xi}(t) =(I_N\otimes cK_1)(L\otimes I_p)X(t) u(t)=(IN⊗cK1)ξ(t)=(IN⊗cK1)(L⊗Ip)X(t)
其中K1K_1K1是待求的控制增益矩阵,ccc为加权参数; -
定义LLL为该系统的Laplacian矩阵,存在一个酉矩阵YYY,使得:
YTLY=diag(λ1,λ2,...λN)Y^TLY=\mathbf{diag}(\lambda_1,\lambda_2,...\lambda_N) YTLY=diag(λ1,λ2,...λN)
其中:λ1=0;λi>0,i∈{2,3,..N}\lambda_1=0;\lambda_i >0,i \in \{ 2,3,..N\}λ1=0;λi>0,i∈{2,3,..N},由于LLL有右特征向量1N\mathbf{1}_N1N,YYY可以写成:
Y=[1NN,M1]Y=[\frac{\mathbf{1}_N}{\sqrt{N}}, M_1] Y=[N1N,M1] -
定义:ε(t)=[ε1(t)T,ε2(t)T,..εN(t)T]T=(YT⊗Ip)ξ(t)\mathbf{\varepsilon}(t)=[\mathbf{\varepsilon}_1(t)^T,\mathbf{\varepsilon}_2(t)^T,..\mathbf{\varepsilon}_N(t)^T]^T=(Y^T\otimes I_p)\mathbf{\xi}(t)ε(t)=[ε1(t)T,ε2(t)T,..εN(t)T]T=(YT⊗Ip)ξ(t),其中ppp为xi(t)\mathbf{x}_i(t)xi(t)的维度。
1.无向连通图定理
引理1.1: 当多智能体系统网络为无向连通图时,系统实现状态一致的充要条件是:
εˉ(t)=[ε2(t)T,ε3(t)T,..εN(t)T]T=0\mathbf{\bar \varepsilon}(t)=[\mathbf{\varepsilon}_2(t)^T,\mathbf{\varepsilon}_3(t)^T,..\mathbf{\varepsilon}_N(t)^T]^T=\mathbf{0} εˉ(t)=[ε2(t)T,ε3(t)T,..εN(t)T]T=0
且εˉ(t)\bar{\varepsilon}(t)εˉ(t)同时也满足:
ε˙(t)=(IN⊗A+cΛN⊗BK1)ε(t)εˉ˙(t)=(IN−1⊗A+cΛN−1⊗BK1)εˉ(t)(∗)\dot \varepsilon(t) = (I_N\otimes A+c\Lambda_N \otimes BK_1)\varepsilon(t)\\ \dot{\bar{\varepsilon}}(t) = (I_{N-1}\otimes A+c\Lambda_{N-1} \otimes BK_1)\bar{\varepsilon}(t) \quad (*) ε˙(t)=(IN⊗A+cΛN⊗BK1)ε(t)εˉ˙(t)=(IN−1⊗A+cΛN−1⊗BK1)εˉ(t)(∗)
其中:ΛN−1=diag(λ2,...λN)\Lambda_{N-1}=diag(\lambda_2,...\lambda_N)ΛN−1=diag(λ2,...λN),ΛN=diag(λ1,λ2,...λN)\Lambda_{N}=diag(\lambda_1,\lambda_2,...\lambda_N)ΛN=diag(λ1,λ2,...λN)。
定理1.1:给定矩阵Q1=Q1T>0Q_1=Q_1^T>0Q1=Q1T>0和R1=R1T>0R_1=R_1^T>0R1=R1T>0,若如下Riccati方程有正定解P1=P1T>0P_1=P_1^T>0P1=P1T>0:
P1A+AP1T+Q1−P1BR1−1BTP1=0P_1A+AP_1^T+Q_1-P_1BR_1^{-1}B^TP_1=\mathbf{0} P1A+AP1T+Q1−P1BR1−1BTP1=0
则系统(∗)(*)(∗)渐进稳定,由引理1.1可知,原系统能达到一致性。
其中系统的控制增益矩阵K1=−R1−1BTP1K_1=-R_1^{-1}B^TP_1K1=−R1−1BTP1,且加权系数ccc满足c≥12mini=2,...Nλi(L)c\geq\frac{1}{2\min_{i=2,...N}{\lambda_i(L)}}c≥2mini=2,...Nλi(L)1。
证明:构造Lyapunov函数V1(t)=0.5εˉT(t)(IN−1⊗P1)εˉ(t)V_1(t)=0.5\bar{\varepsilon}^T(t)(I_{N-1}\otimes P_1)\bar{\varepsilon}(t)V1(t)=0.5εˉT(t)(IN−1⊗P1)εˉ(t),其满足:
V1˙(t)=0.5εˉ˙T(t)(IN−1⊗P1)εˉ(t)+0.5εˉT(t)(IN−1⊗P1)εˉ˙(t)=εˉT(t)(IN−1⊗P1)εˉ˙(t)=εˉ(t)T(IN−1⊗P1)(IN−1⊗A+cΛN−1⊗BK1)εˉ(t)=εˉT(t)(IN−1⊗P1A+cΛN−1⊗P1BK1)εˉ(t)=εˉT(t)(IN−1⊗P1A−cΛN−1⊗P1BR1−1BTP1)εˉ(t)\dot{V_1}(t)=0.5\dot{\bar{\varepsilon}}^T(t)(I_{N-1}\otimes P_1)\bar{\varepsilon}(t)+0.5\bar{\varepsilon}^T(t)(I_{N-1}\otimes P_1)\dot{\bar{\varepsilon}}(t)\\ =\bar{\varepsilon}^T(t)(I_{N-1}\otimes P_1)\dot{\bar{\varepsilon}}(t)\\=\bar{\varepsilon}(t)^T(I_{N-1}\otimes P_1)(I_{N-1}\otimes A+c\Lambda_{N-1} \otimes BK_1)\bar{\varepsilon}(t)\\=\bar{\varepsilon}^T(t)(I_{N-1}\otimes P_1A+c\Lambda_{N-1}\otimes P_1BK_1)\bar{\varepsilon}(t)\\=\bar{\varepsilon}^T(t)(I_{N-1}\otimes P_1A-c\Lambda_{N-1}\otimes P_1BR_1^{-1}B^TP_1)\bar{\varepsilon}(t) V1˙(t)=0.5εˉ˙T(t)(IN−1⊗P1)εˉ(t)+0.5εˉT(t)(IN−1⊗P1)εˉ˙(t)=εˉT(t)(IN−1⊗P1)εˉ˙(t)=εˉ(t)T(IN−1⊗P1)(IN−1⊗A+cΛN−1⊗BK1)εˉ(t)=εˉT(t)(IN−1⊗P1A+cΛN−1⊗P1BK1)εˉ(t)=εˉT(t)(IN−1⊗P1A−cΛN−1⊗P1BR1−1BTP1)εˉ(t)
由于c≥12mini=2,...Nλi(L)c\geq\frac{1}{2\min_{i=2,...N}{\lambda_i(L)}}c≥2mini=2,...Nλi(L)1,因此cΛN−1≥IN−12c\Lambda_{N-1}\geq\frac{I_{N-1}}{2}cΛN−1≥2IN−1。带入上式有:
V1˙(t)=εˉT(t)(IN−1⊗P1A−cΛN−1⊗P1BR1−1BTP1)εˉ(t)≤εˉT(t)(IN−1⊗P1A−IN−12⊗P1BR1−1BTP1)εˉ(t)=εˉT(t)(IN−12⊗(P1A+ATP1)−IN−12⊗P1BR1−1BTP1)εˉ(t)=−12εˉT(t)(IN−1⊗Q1)εˉ(t)\dot{V_1}(t)=\bar{\varepsilon}^T(t)(I_{N-1}\otimes P_1A-c\Lambda_{N-1}\otimes P_1BR_1^{-1}B^TP_1)\bar{\varepsilon}(t)\\ \leq \bar{\varepsilon}^T(t)(I_{N-1}\otimes P_1A-\frac{I_{N-1}}{2}\otimes P_1BR_1^{-1}B^TP_1)\bar{\varepsilon}(t)\\=\bar{\varepsilon}^T(t)( \frac{I_{N-1}}{2}\otimes (P_1A+A^TP_1) -\frac{I_{N-1}}{2}\otimes P_1BR_1^{-1}B^TP_1)\bar{\varepsilon}(t)\\=-\frac{1}{2}\bar{\varepsilon}^T(t)(I_{N-1}\otimes Q_1)\bar{\varepsilon}(t) V1˙(t)=εˉT(t)(IN−1⊗P1A−cΛN−1⊗P1BR1−1BTP1)εˉ(t)≤εˉT(t)(IN−1⊗P1A−2IN−1⊗P1BR1−1BTP1)εˉ(t)=εˉT(t)(2IN−1⊗(P1A+ATP1)−2IN−1⊗P1BR1−1BTP1)εˉ(t)=−21εˉT(t)(IN−1⊗Q1)εˉ(t)
由直积的性质有:
λmin(IN−1⊗Q1)=λmin(Q1)λmax(IN−1⊗P1)=λmax(P1)\lambda_{\min}(I_{N-1}\otimes Q_1)=\lambda_{\min}(Q_1)\\ \lambda_{\max}(I_{N-1}\otimes P_1)=\lambda_{\max}(P_1) λmin(IN−1⊗Q1)=λmin(Q1)λmax(IN−1⊗P1)=λmax(P1)
由矩阵的极大极小值原理:
V1˙(t)V1(t)=−12εˉT(t)(IN−1⊗Q1)εˉ(t)12εˉT(t)(IN−1⊗P1)εˉ(t)≤−λmin(Q1)εˉT(t)εˉ(t)λmax(P1)εˉT(t)εˉ(t)=−λmin(Q1)λmax(P1)=−δ\frac{\dot{V_1}(t)}{V_1(t)}=\frac{-\frac{1}{2}\bar{\varepsilon}^T(t)(I_{N-1}\otimes Q_1)\bar{\varepsilon}(t)}{\frac{1}{2}\bar{\varepsilon}^T(t)(I_{N-1}\otimes P_1)\bar{\varepsilon}(t)}\leq-\frac{\lambda_{\min}(Q_1)\bar{\varepsilon}^T(t)\bar{\varepsilon}(t)}{\lambda_{\max}(P_1)\bar{\varepsilon}^T(t)\bar{\varepsilon}(t) }=-\frac{\lambda_{\min}(Q_1)}{\lambda_{\max}(P_1)}=-\delta V1(t)V1˙(t)=21εˉT(t)(IN−1⊗P1)εˉ(t)−21εˉT(t)(IN−1⊗Q1)εˉ(t)≤−λmax(P1)εˉT(t)εˉ(t)λmin(Q1)εˉT(t)εˉ(t)=−λmax(P1)λmin(Q1)=−δ
解上述不等式有:
V1(t)≤V1(0)e−δtV_1(t)\leq V_1(0)e^{-\delta t} V1(t)≤V1(0)e−δt
带入V1(t)≥0.5λmin(P1)∣∣εˉ(t)∣∣2V_1(t)\geq 0.5\lambda_{\min}(P_1)||\bar{\varepsilon}(t)||^2V1(t)≥0.5λmin(P1)∣∣εˉ(t)∣∣2 和V1(0)≤0.5λmax(P1)∣∣εˉ(0)∣∣2V_1(0)\leq 0.5\lambda_{\max}(P_1)||\bar{\varepsilon}(0)||^2V1(0)≤0.5λmax(P1)∣∣εˉ(0)∣∣2有:
∣∣εˉ(t)∣∣≤λmax(P1)λmin(P1)∣∣εˉ(0)∣∣e−δt2||\bar{\varepsilon}(t)||\leq \sqrt\frac{\lambda_{\max}(P_1)}{\lambda_{\min}(P_1)}||\bar{\varepsilon}(0)||e^{\frac{-\delta t}{2}} ∣∣εˉ(t)∣∣≤λmin(P1)λmax(P1)∣∣εˉ(0)∣∣e2−δt
因此上述系统(*)是一致指数稳定的,其必然是渐进稳定的。
2.仿真
2.1 问题
设固定翼无人机集群中每个无人机的俯仰方向运动模型的线性化系统方程为:
(α˙(t)q˙(t))=(−1.1750.9871−8.458−0.8776)(α(t)q(t))+(−0.194−0.03593−19.29−3.803)(δiail(t)δirud(t))\begin{pmatrix} \dot{\alpha}(t) \\ \dot{q}(t) \end{pmatrix} = \begin{pmatrix} -1.175&0.9871\\-8.458&-0.8776 \end{pmatrix} \begin{pmatrix} {\alpha}(t) \\ {q}(t) \end{pmatrix}+ \begin{pmatrix} -0.194&-0.03593\\-19.29&-3.803 \end{pmatrix}\begin{pmatrix} {\delta}_i^{\mathbf{ail}}(t) \\ {\delta}_i^{\mathbf{rud}}(t) \end{pmatrix} (α˙(t)q˙(t))=(−1.175−8.4580.9871−0.8776)(α(t)q(t))+(−0.194−19.29−0.03593−3.803)(δiail(t)δirud(t))
其中:α(t)\alpha(t)α(t):无人机俯仰角;qi(t)q_i(t)qi(t):无人机俯仰角速度;
δail(t)\delta^{\mathbf{ail}}(t)δail(t):副翼操作指令;δrud(t)\delta^{\mathbf{rud}}(t)δrud(t):升降舵操作指令;
先有3架无人机,其通信拓扑图如下:

3架无人机的初值为:
(α1(0)q1(0))=(10−3);(α2(0)q2(0))=(−72);(α3(0)q3(0))=(4−1)\begin{pmatrix} {\alpha}_1(0) \\ {q}_1(0) \end{pmatrix}=\begin{pmatrix} 10\\ -3\end{pmatrix}; \begin{pmatrix} {\alpha}_2(0) \\ {q}_2(0) \end{pmatrix}=\begin{pmatrix} -7\\ 2\end{pmatrix}; \begin{pmatrix} {\alpha}_3(0) \\ {q}_3(0) \end{pmatrix}=\begin{pmatrix} 4\\ -1\end{pmatrix} (α1(0)q1(0))=(10−3);(α2(0)q2(0))=(−72);(α3(0)q3(0))=(4−1)
设计控制策略使3架无人机能完成俯仰角与俯仰角速度上的一致性。
2.2 求解
A=(−1.1750.9871−8.458−0.8776)A=\begin{pmatrix} -1.175&0.9871\\-8.458&-0.8776 \end{pmatrix}A=(−1.175−8.4580.9871−0.8776),B=(−0.194−0.03593−19.29−3.803)B=\begin{pmatrix} -0.194&-0.03593\\-19.29&-3.803 \end{pmatrix}B=(−0.194−19.29−0.03593−3.803),设R1=50I2R_1=50I_2R1=50I2,Q1=10I2Q_1=10I_2Q1=10I2。
利用Matlab中的 care求解Riccati方程P1A+AP1T+Q1−P1BR1−1BTP1=0P_1A+AP_1^T+Q_1-P_1BR_1^{-1}B^TP_1=\mathbf{0}P1A+AP1T+Q1−P1BR1−1BTP1=0得到:
P1=(6.1743−0.2904−0.29040.9991)=P1T>0P_1 = \begin{pmatrix} 6.1743&-0.2904\\-0.2904&0.9991 \end{pmatrix} =P_1^T>0 P1=(6.1743−0.2904−0.29040.9991)=P1T>0
代码如下:
>> A=[-1.175 0.9871;-8.458 -0.8776];
>> B = [-0.194 -0.03593;-19.29 -3.803];
>> R1 = 50*eye(2);
>> Q1 = 10*eye(2);
>> P1 = care(A,B,Q1,R1)P1 =6.1743 -0.2904-0.2904 0.9991
故由定理1.1多智能体系统可以实现一致性。
可以知道在验证线性系统一致性的过程中并没有考虑个体间的通信Laplacian矩阵。这说明同构多智能体线性系统的一致性本质上与其Laplacian矩阵无关!!!
可以得到其Laplacian矩阵为:
L=(1−10−12−10−11)L=\begin{pmatrix} 1&-1&0\\-1&2&-1\\0&-1&1 \end{pmatrix} L=1−10−12−10−11
其中矩阵K1=−R1−1BTP1=(−0.08810.3843−0.01770.0758)K_1=-R_1^{-1}B^TP_1=\begin{pmatrix} -0.0881 &0.3843\\-0.0177&0.0758\end{pmatrix}K1=−R1−1BTP1=(−0.0881−0.01770.38430.0758),ccc要满足c≥12mini=2,...Nλi(L)=0.5c\geq\frac{1}{2\min_{i=2,...N}{\lambda_i(L)}}=0.5c≥2mini=2,...Nλi(L)1=0.5,取c=0.6c=0.6c=0.6。得到控制策略:
u(t)=cK1ξ(t)=(I2⊗(−0.05290.2306−0.01060.0455))ξ(t)\mathbf{u}(t)=cK_1\mathbf{\xi}(t)=(I_2\otimes\begin{pmatrix} -0.0529 & 0.2306\\-0.0106 &0.0455\end{pmatrix})\mathbf{\xi}(t) u(t)=cK1ξ(t)=(I2⊗(−0.0529−0.01060.23060.0455))ξ(t)
下面用代码验证其可行性:
这里需要将连续系统零阶离散化,因此需要的采样时间很重要,不同采样时间会导致最后结果不收敛:
当Δt=0.04s\Delta t=0.04sΔt=0.04s时:

当Δt=0.06s\Delta t=0.06sΔt=0.06s时:

可以看到差距甚大,几乎不能用,因此说明了采样时间的重要性。同时也说明了该一致性控制策略有效!
3.代码
clc,clear;
A=[-1.175 0.9871;-8.458 -0.8776];
B = [-0.194 -0.03593;-19.29 -3.803];
c = 0.6;
K1 = [-0.0881 0.3843;...-0.0177 0.0758];
L = [1 -1 0;-1 2 -1;0 -1 1];
x1 = [10,-3]';x1_array = x1;
x2 = [-7,2]'; x2_array = x2;
x3 = [4,-1]'; x3_array = x3;
x_0 = [x1,x2,x3];
% 设置采样时间
delta_t = 0.04;
% num个时间步长内仿真
num = 100;
x = [x1;x2;x3];
%x_array = zeros(3*2,num);
for k = 1:num% 设计总的控制策略U = kron(L,c*K1*eye(2))*x;u1 = U(1:2);u2 = U(3:4);u3 = U(5:6);
for i = 1:3 x1 = (eye(2) +delta_t*A)*x1 + delta_t*B*u1; x2 = (eye(2) +delta_t*A)*x2 + delta_t*B*u2;x3 = (eye(2) +delta_t*A)*x3 + delta_t*B*u3;
end
x = [x1;x2;x3];
x1_array = [x1_array,x1];
x2_array = [x2_array,x2];
x3_array = [x3_array,x3];
end
% 下面开始画图
subplot(121)
hold on;grid on;box on;
plot(delta_t*(1:num),x1_array(1,1:num),'r.-');
plot(delta_t*(1:num),x2_array(1,1:num),'g.-');
plot(delta_t*(1:num),x3_array(1,1:num),'b.-');
xlabel('时间/s');ylabel('俯仰角');
legend('无人机1','无人机2','无人机3');
subplot(122)
hold on;grid on;box on;
plot(delta_t*(1:num),x1_array(2,1:num),'r.-');
plot(delta_t*(1:num),x2_array(2,1:num),'g.-');
plot(delta_t*(1:num),x3_array(2,1:num),'b.-');
xlabel('时间/s');ylabel('俯仰角速度');
legend('无人机1','无人机2','无人机3');
相关文章:

多智能体集群协同控制笔记(1):线性无领航多智能体系统的一致性
对于连续时间高阶线性多智能体系统的状态方程为: x˙i(t)Axi(t)Bui(t),i1,2..N\dot {\mathbf{x}}_i(t)A\mathbf{x}_i(t)B\mathbf{u}_i(t),i1,2..N x˙i(t)Axi(t)Bui(t),i1,2..N 下标iii代表第iii个智能体,ui(t)∈Rq1\mathbf{u}_i(t)\in R^{q \time…...

hadoop-Yarn资源调度器【尚硅谷】
大数据学习笔记 Yarn资源调度器 Yarn是一个资源调度平台,负责为运算程序提供服务器运算资源,相当于一个分布式的操作系统平台,而MapReduce等运算程序则相当于运行与操作系统之上的应用程序。 (也就是负责MapTask、ReduceTask等任…...

聊聊如何避免多个jar通过maven打包成一个jar,多个同名配置文件发生覆盖问题
前言 不知道大家在开发的过程中,有没有遇到这种场景,外部的项目想访问内部nexus私仓的jar,因为私仓不对外开放,导致外部的项目没法下载到私仓的jar,导致项目因缺少jar而无法运行。 通常遇到这种场景,常用…...

Flume 使用小案例
案例一:采集文件内容上传到HDFS 1)把Agent的配置保存到flume的conf目录下的 file-to-hdfs.conf 文件中 # Name the components on this agent a1.sources r1 a1.sinks k1 a1.channels c1 # Describe/configure the source a1.sources.r1.type spoo…...

DLO-SLAM代码阅读
文章目录DLO-SLAM点评代码解析OdomNode代码结构主函数 main激光回调函数 icpCB初始化 initializeDLO重力对齐 gravityAlign点云预处理 preprocessPoints关键帧指标 computeMetrics设定关键帧阈值setAdaptiveParams初始化目标数据 initializeInputTarget设置源数据 setInputSour…...
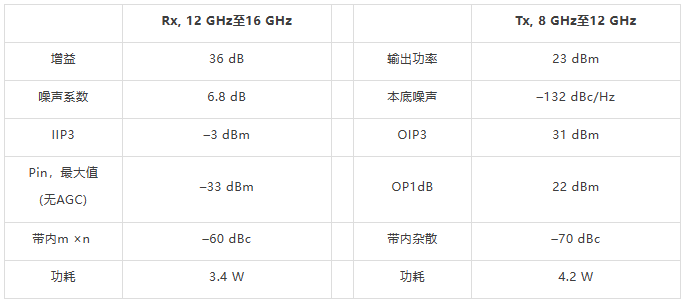
X和Ku波段小尺寸无线电设计
卫星通信、雷达和信号情报(SIGINT)领域的许多航空航天和防务电子系统早就要求使用一部分或全部X和Ku频段。随着这些应用转向更加便携的平台,如无人机(UAV)和手持式无线电等,开发在X和Ku波段工作,同时仍然保持极高性能水平的新型小尺寸、低功耗…...

推荐算法 - 汇总
本文主要对推荐算法整体知识点做汇总,做到总体的理解;深入理解需要再看专业的材料。推荐算法的意义推荐根据用户兴趣和行为特点,向用户推荐所需的信息或商品,帮助用户在海量信息中快速发现真正所需的商品,提高用户黏性…...
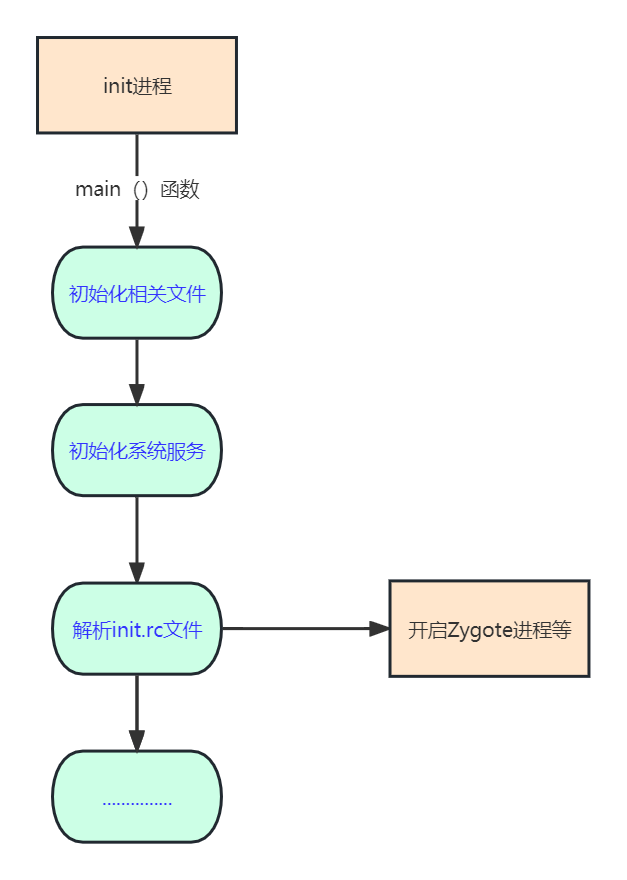
Android 系统的启动流程
前言:从开机的那一刻,到开机完成后launcher将所有应用进行图标展示的这个过程,大概会有哪一些操作?执行了哪些代码?作为Android开发工程师的我们,有必要好好的梳理一遍。既然要梳理Android系统的启动流程&a…...

自学5个月Java找到了9K的工作,我的方式值得大家借鉴 第二部分
我的学习心得,我认为能不能自学成功的要素有两点。 第一点就是自身的问题,虽然想要转行学习Java的人很多,但是非常强烈的想要转行学好的人是小部分。而大部分人只是抱着试试的心态来学习Java,这是完全不可能的。所以能不能学成Jav…...

Vue 3 第五章:reactive全家桶
文章目录1. reactive1.1. reactive函数创建一个响应式对象1.2. 修改reactive创建的响应式对象的属性2. readOnly2.1. 使用 readonly 函数创建一个只读的响应式对象2.2. 如何修改嵌套在只读响应式对象中的对象?3. shallowReactive3.1. 使用 shallowReactive 函数创建一个浅层响…...

【联机对战】微信小程序联机游戏开发流程详解
现有一个微信小程序叫中国象棋项目,棋盘类的单机游戏看着有缺少了什么,现在给补上了,加个联机对战的功能,增加了可玩性,对新手来说,实现联机游戏还是有难度的,那要怎么实现的呢,接下…...

优化基于axios接口管理的骚操作
优化基于axios接口管理的骚操作! 本文针对中大型的后台项目的接口模块优化,在不影响项目正常运行的前提下,增量更新。 强化功能 1.接口文件写法简化(接口模块半自动化生成) 2.任务调度、Loading调度(接口层…...
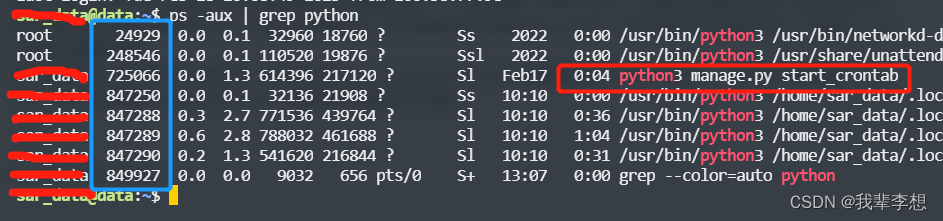
【Django功能开发】如何正确使用定时任务(启动、停止)
系列文章目录 【Django开发入门】ORM的增删改查和批量操作 【Django功能开发】编写自定义manage命令 文章目录系列文章目录前言一、django定时任务二、django-apscheduler基本使用1.安装django-apscheduler2.配置settings.py的INSTALLED_APPS3.通过命令生成定时记录表3.如何创…...
7个好用到爆的音频、配乐素材网站,BGM都在这里了
现在只要有一部手机,人人都能成为视频创作者。一个好的视频不能缺少的就是内容、配乐,越来越注重版权的当下,音效素材使用不当造成侵权的案例层出不穷。为了避免侵权,找素材让很多创作者很头疼。 今天我就整理了7个可以免费下载&…...
JUC(二)
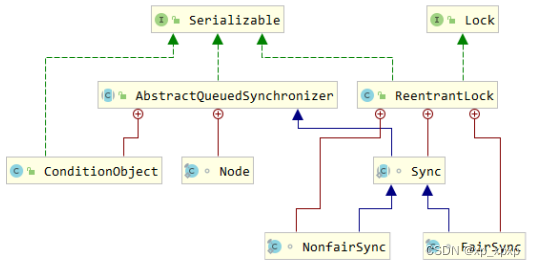
1.可重入锁–ReentrantLock原理 1.1.非公平锁的实现原理 1.1.1.加锁解锁流程 1>.先从构造器开始看,默认为非公平锁,可以在构造函数中设置参数指定公平锁 public ReentrantLock() {sync = new NonfairSync(); }public ReentrantLock...
ATS认证教学
我用的版本是ATS7.11、系统版本是用最新的ios13.2.1 定义 ATS旨在分析通过UART、USB和蓝牙传输传输的iAP流量、通过USB和无线(蓝牙和Wi-Fi)传输的CarPlay流量、通过Wi-Fi传输的AirPlay 2流量以及闪电音频流量。 ATS是Apple’s Accessory Test System的…...
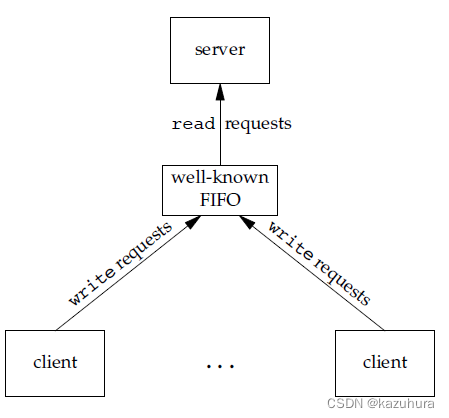
【操作系统】进程管理
进程与线程 1. 进程 进程是资源分配的基本单位 进程控制块 (Process Control Block, PCB) 描述进程的基本信息和运行状态,所谓的创建进程和撤销进程,都是指对 PCB 的操作。 下图显示了 4 个程序创建了 4 个进程,这 4 个进程可以并发地执行…...

一分钟掌握技术术语:API(接口)
很多产品经理在项目开发过程中经常听到:你调我这个接口就好了;这个功能你写个接口给我;有什么不懂的就看下API接口文档。 开发经常说的接口是什么意思呢?术语解释:API(Application Programming Interface&…...
RabbitMQ之交换机
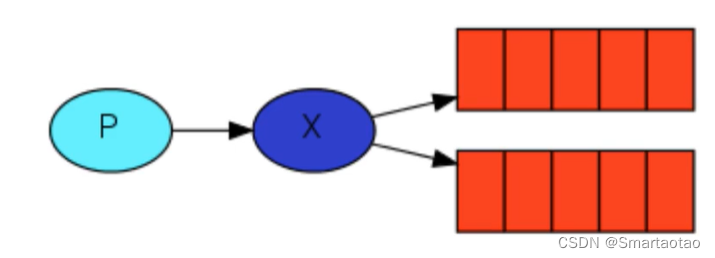
交换机 在上一节中,我们创建了一个工作队列。我们假设的是工作队列背后,每个任务都恰好交付给一个消费者(工作进程)。在这一部分中,我们将做一些完全不同的事情-我们将消息传达给多个消费者。这种模式称为“发布/订阅”. 为了说明这种模式,我们将构建一个简单的日志系统。它…...
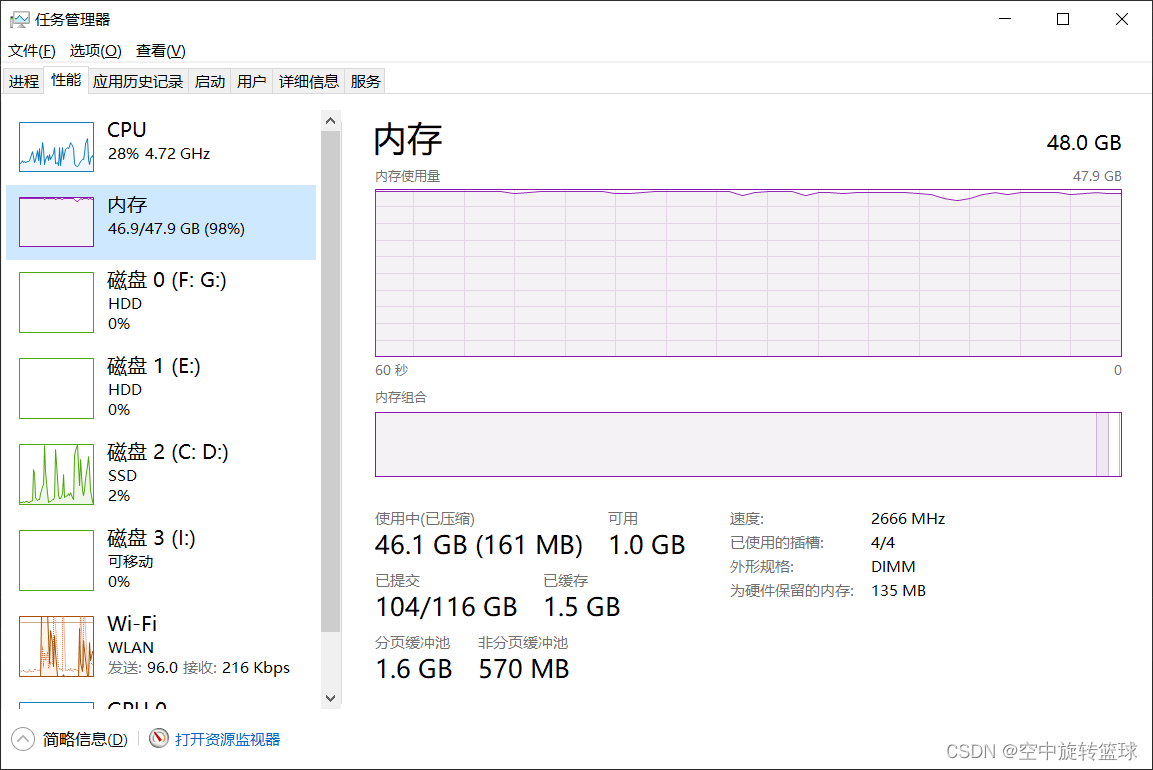
Tensorflow深度学习对遥感图像分类,内存不够怎么办?
问题描述在使用Tensorflow-cpu对图像分类的时候,在预读数据过程中,由于数据量过大,内存不足,导致计算失败。使用环境:win10系统 Pycharm tensorflow-cpu2.5.0 CPU: i7 8700 内存64G图1 CPU配置图图2 内存信息图使用数据…...

golang循环变量捕获问题
在 Go 语言中,当在循环中启动协程(goroutine)时,如果在协程闭包中直接引用循环变量,可能会遇到一个常见的陷阱 - 循环变量捕获问题。让我详细解释一下: 问题背景 看这个代码片段: fo…...

Appium+python自动化(十六)- ADB命令
简介 Android 调试桥(adb)是多种用途的工具,该工具可以帮助你你管理设备或模拟器 的状态。 adb ( Android Debug Bridge)是一个通用命令行工具,其允许您与模拟器实例或连接的 Android 设备进行通信。它可为各种设备操作提供便利,如安装和调试…...

通过Wrangler CLI在worker中创建数据库和表
官方使用文档:Getting started Cloudflare D1 docs 创建数据库 在命令行中执行完成之后,会在本地和远程创建数据库: npx wranglerlatest d1 create prod-d1-tutorial 在cf中就可以看到数据库: 现在,您的Cloudfla…...

第25节 Node.js 断言测试
Node.js的assert模块主要用于编写程序的单元测试时使用,通过断言可以提早发现和排查出错误。 稳定性: 5 - 锁定 这个模块可用于应用的单元测试,通过 require(assert) 可以使用这个模块。 assert.fail(actual, expected, message, operator) 使用参数…...

苍穹外卖--缓存菜品
1.问题说明 用户端小程序展示的菜品数据都是通过查询数据库获得,如果用户端访问量比较大,数据库访问压力随之增大 2.实现思路 通过Redis来缓存菜品数据,减少数据库查询操作。 缓存逻辑分析: ①每个分类下的菜品保持一份缓存数据…...

土地利用/土地覆盖遥感解译与基于CLUE模型未来变化情景预测;从基础到高级,涵盖ArcGIS数据处理、ENVI遥感解译与CLUE模型情景模拟等
🔍 土地利用/土地覆盖数据是生态、环境和气象等诸多领域模型的关键输入参数。通过遥感影像解译技术,可以精准获取历史或当前任何一个区域的土地利用/土地覆盖情况。这些数据不仅能够用于评估区域生态环境的变化趋势,还能有效评价重大生态工程…...

IoT/HCIP实验-3/LiteOS操作系统内核实验(任务、内存、信号量、CMSIS..)
文章目录 概述HelloWorld 工程C/C配置编译器主配置Makefile脚本烧录器主配置运行结果程序调用栈 任务管理实验实验结果osal 系统适配层osal_task_create 其他实验实验源码内存管理实验互斥锁实验信号量实验 CMISIS接口实验还是得JlINKCMSIS 简介LiteOS->CMSIS任务间消息交互…...

全志A40i android7.1 调试信息打印串口由uart0改为uart3
一,概述 1. 目的 将调试信息打印串口由uart0改为uart3。 2. 版本信息 Uboot版本:2014.07; Kernel版本:Linux-3.10; 二,Uboot 1. sys_config.fex改动 使能uart3(TX:PH00 RX:PH01),并让boo…...

Web 架构之 CDN 加速原理与落地实践
文章目录 一、思维导图二、正文内容(一)CDN 基础概念1. 定义2. 组成部分 (二)CDN 加速原理1. 请求路由2. 内容缓存3. 内容更新 (三)CDN 落地实践1. 选择 CDN 服务商2. 配置 CDN3. 集成到 Web 架构 …...

HDFS分布式存储 zookeeper
hadoop介绍 狭义上hadoop是指apache的一款开源软件 用java语言实现开源框架,允许使用简单的变成模型跨计算机对大型集群进行分布式处理(1.海量的数据存储 2.海量数据的计算)Hadoop核心组件 hdfs(分布式文件存储系统)&a…...
