Robust taboo search for the quadratic assignment problem-二次分配问题的鲁棒禁忌搜索
文章目录
- 摘要
- 关键字
- 结论
- 研究背景
- 1. Introduction
- 常用基础理论知识
- 2. The quadratic assignment problem
- 3. Taboo search
- 3.1. Moves
- 3.2 Taboo list
- 3.3. Aspiration function
- 3.4. Taboo list size
- 4. Random problems
- 5. Parallel taboo search
- 研究内容、成果
- 7. Conclusion
- 潜在研究点
- 文献链接
摘要
目的:为了提高禁忌搜索的速度,提出了两种并行化方法,并显示了它们对于与问题规模成正比的处理器数量的效率。还提出了一种生成随机问题的简单方法
优势:更少的复杂性和更少的参数。
关键字
组合优化;禁忌搜索;并行算法;二次分配问题;效率
结论
研究背景
1. Introduction
二次分配问题 (QAP) 非常困难,以至于 Steinberg在 1961 年提出的尺寸为 36 的实例尚未得到解决。
本文的目标是为 QAP 提出一种更稳健的 TS 形式,它具有最少的参数数量,并且非常容易实现,能够获得与先前找到的最佳解决方案相当的解决方案,而无需多次传递和更改参数值。
常用基础理论知识
2. The quadratic assignment problem
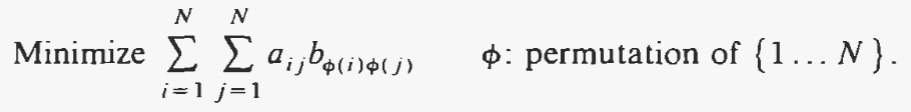
可以自然地用 QAP 表达的问题的示例包括:
- 芯片中逻辑模块的放置,使得连接的总长度最小化;
- 在大型医院中心分配医疗服务。
3. Taboo search
TS的主要思想可以简单概括如下。第一个要素是定义一个邻域,或者一组可以应用于给定解决方案以产生新解决方案的移动。在所有邻近的解决方案中,TS 寻求一个具有最佳启发式评估的解决方案。在最简单的情况下,这样的评估决定了最能改善目标函数的移动的选择。如果没有改进的移动(表明一种局部最优),TS 选择一个对目标函数降级最少的移动。为了避免回到刚刚访问的局部最优,现在必须禁止反向移动。这是通过将这一举动(或更准确地说是该举动的特征)存储在通常像循环列表一样管理并称为禁忌列表的数据结构中来完成的。该列表包含许多定义禁止(禁忌)动作的元素;参数s称为禁忌列表大小。然而,禁忌清单可能会禁止某些相关或有趣的举措,例如那些导致比迄今为止发现的最佳解决方案更好的解决方案的举措。因此,引入了一个愿望标准,如果禁忌动作被认为是有趣的,则允许选择禁忌动作。 TS 的完整版本包含附加元素,但我们将展示如何单独使用这些基本概念来构建 QAP 的有效实现。
3.1. Moves
非常适合此问题的自然移动类型包括交换两个单元,以便每个单元占据另一个单元先前占据的位置。从放置 开始,通过排列单元 r 和 s 获得相邻放置 7r:

如果矩阵是对称的并且具有零对角线(就像“经典”示例的情况一样),则移动的值,写作:

如果矩阵不对称和/或没有零对角线,则表达式(仍可在 O(N) 中计算)会稍微复杂一些。 [3]。
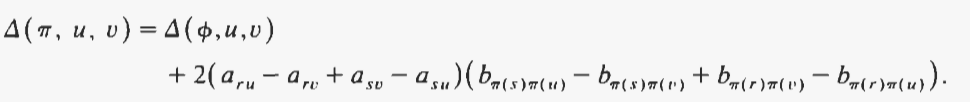
对动作质量的快速评估是提高搜索效率的重要因素。该评估可能与 Fiechter [7] 的旅行推销员应用程序或 Taillard [19] 的流水车间排序中一样精确,或者与 Taillard [20] 的作业车间调度中一样近似。此外,这些动作必须具有与所考虑的问题相关的良好特性。对于 QAP 来说,采用将单元 r 插入到排列 q) 中与单元 s 相邻的移动是不合适的,因为这会改变排列中 r 和 s 之间每个单元的位置 - 一场真正的灾难!
3.2 Taboo list
我们现在必须定义禁忌列表元素的类型。 Skorin-Kapov [16] 提出禁止交换在前 s 次迭代期间交换过的两个单元。形式上,禁忌列表由不能交换的单元对 (i, j) 组成。列表的禁止可以用整数的二维数组来实现,其中元素(i,j)标识未来迭代的值,在未来迭代中这两个单元可以再次彼此交换。这样一来,检验一个动作是否禁忌,只需要一次比较即可。在恒定时间内评估禁忌条件非常重要,以便在与其大小成比例的时间内评估邻域,从而避免搜索复杂性的增长。
在他的文凭项目中,Rogger 尝试了多种类型的禁忌列表,我们选择了如果列表的大小 s 改变则证明最方便的一种,因为我们采用了以下规则:改变此参数的值(Glover [11] 描述了一般设置中此类列表的优点)。具体来说,我们的禁忌列表构建如下:对于每个单位和位置,记录该单位占据该位置的最新迭代。如果移动将两个互换的单位分配到它们在最近迭代中占据的位置,则该移动是禁忌。这种类型的列表提供的结果与在给定“最佳”大小时使用 Skorin-Kapov 提出的类型获得的结果相当,但对参数 s 不太敏感。
3.3. Aspiration function
对于每个问题,我们都使用经典的愿望函数,如果它导致的解决方案比迄今为止找到的最佳解决方案更好,则允许选择禁忌举措。然而,对于某些问题的最著名的解决方案并不总是能够通过这种最小的实现来获得,即仅使用一种类型的移动、一个禁忌列表和微不足道的愿望功能。仔细检查实现表现较差的问题(特别是 Elshafei [6] 提出的问题),揭示了概念上的错误:这些问题有一个非常特殊的流矩阵,其中包含大量空值或非常小的值和一些非常小的值。高流量。如果搜索在某个时刻未能在局部最优处找到高流量的单元,那么 TS 将以较小的成本执行移动,因为关键单元的第一次交换将大大增加目标函数的值。
我们提出的克服这一困难的技巧非常简单:对于流量或成本非常异构的问题,如果交易所将两个单元放置在不同位置,则移动将通过愿望标准并被选择,解决方案质量完全是从属衡量标准它们在最后 t 次迭代中没有占用。从概念上讲,该函数可以被视为一个长期的多元化过程,每当某些单位成功满足标准时,该函数就会被激活以禁止无法满足其条件的移动。
3.4. Taboo list size
禁忌清单大小的选择至关重要;如果它的值太小,搜索过程中可能会发生循环,而如果它的值太大,有吸引力的移动可能会被禁止,导致探索较低质量的解决方案,产生大量的迭代来找到所需的解决方案。
然而,认为循环现象总是作为小禁忌列表大小的函数出现的想法是错误的,因为我们观察到,对于 Nugent 等人的大小 15 的问题。 [13],禁忌列表大小设置为 s = 30 的循环,对于 26 到 29 之间的大小没有观察到这种循环。为了克服与搜索最佳禁忌列表大小相关的问题,我们提出以下技巧:我们建议在搜索过程中随机更改该值,而不是在整个搜索过程中将大小 s 固定为恒定值。实际上,s 将在 Smin 和 Smax = Smin + A 之间选择,并且经常更改,例如每 2’Smax x 迭代(以便有一定的概率以 s = Smax 执行某些迭代)。
在图 1 中,我们感兴趣的是必须赋予 Smin 的实用值和 A 来解决(最优)N = 15 的 Nugent 问题。当我们从独立的初始解开始并使用少于 10000 次迭代成功找到最优解 30 次时,我们在图中用黑色方块绘制。必须注意的是,当 Smin 和 A 设置为“最佳”值时,允许的迭代次数大约是解决该问题所需的平均迭代次数的 20 倍。
在图 1 中,我们首先注意到随机禁忌列表大小 (A > 0) 的引入使得搜索更加可靠。其次,Smin 和 A 的实际取值范围非常广泛。

事实上,对于大多数问题,我们使用 Smin = [0.9 N] 和 Smax = [1.1 N] 找到了迄今为止已知的最佳解决方案。然而,对于小问题(N <= 15)和非正则矩阵问题(Elshafei,Steinberg)或大问题(Skorin-Kapov,Krarup),使用稍大的禁忌列表大小有时可以更快地找到这些解决方案,其中使用第二个愿望功能时,禁忌列表的大小必须减少,大约30%。第二个愿望函数的参数 t 很大程度上取决于问题。对于最不规则的问题(Elshafei),t 设置为 400,对于较大的问题,它设置为 3000 到 10000 之间。
在图 2 中,我们感兴趣的是寻找次优解决方案的平均迭代次数,这是斯坦伯格问题的第一个实例。因此,我们尝试“解决”这个问题 30 次,从独立的初始解决方案开始,最多允许 500000 次迭代。这是针对 3 个 A 值(0、5 和 10)和 7 个 Smin 值(0、5 … 30)完成的。
当禁忌列表大小固定(A = 0)时,充分选择它很重要:对于我们的示例,我们观察到大小小于 10 的循环,而最佳大小约为 20,并且平均迭代次数增加对于大小为 30 的情况,大约为 50%。但是随机性的引入(A = 5 或 A = 10)使得能够以更可靠的方式找到搜索的解(Smin 的良好值的间隔更大)并且与固定大小相比,需要更少的迭代次数 (- 30%)。
4. Random problems
文献中发表的问题有一个主要缺点:复制和使用数据可能很困难,因为矩阵记录在大量表格中,有时以不可读的方式打印。因此,我们提出了一种自动生成问题的简单方法;这些问题通常比已发布的问题更难解决(使用我们的 TS),因为可以常规验证次优解决方案的最大问题的大小为 35 到 40,而我们很可能已经最优地解决了 Steinberg 的问题( N = 36)和斯科林卡波夫(N = 42 至 N = 64)。在我们的生成过程中,距离和流量矩阵的系数是整数,在0到99(包含)之间随机均匀生成。随机数生成器,在 Bratley 等人的书中进行了分析。 [1],基于递归公式:
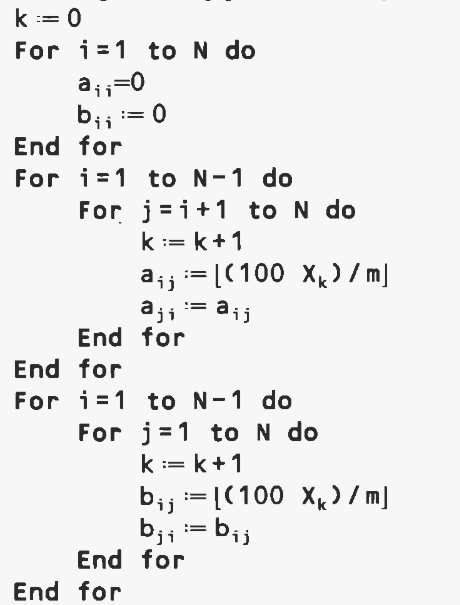
5. Parallel taboo search
研究内容、成果
7. Conclusion
我们在本文中表明,使用基于 TS 的过程并先验地固定其参数,可以找到非常好的 QAP 解决方案。特别是,如果允许 N2 迭代并且禁忌列表大小在问题大小的 10% 范围内随机变化,则有可能获得高质量的解决方案,这更多地取决于问题的类型而不是问题的大小,对于 N >= 20。
我们的 TS 的实现除了简单之外,还将 QAP 的早期 TS 实现的计算复杂度降低了 N 倍,并且通过以下方式可以将复杂度再次降低 N 倍:使用与 N 成比例的处理器数量。结果表明,使用基本 TS(一个禁忌列表和琐碎的愿望函数)对于大多数大小不超过 30 的问题效果很好。对于更大的问题,使用另一个提出了愿望函数 - 添加一个新参数,但不改变算法的复杂性(工作和内存要求) - 并且一些大小高达 64 的问题可能无法得到最佳解决。然而,我们认为寻找更大问题的次优解决方案必须通过另一个过程来完成,例如使用更复杂的 TS 概念(目标分析或更复杂的长期记忆)。最后,给出了一种生成随机问题的可靠方法,这大大减少了获取随机问题实例所需的工作。
潜在研究点
文献链接
相关文章:
Robust taboo search for the quadratic assignment problem-二次分配问题的鲁棒禁忌搜索
文章目录 摘要关键字结论研究背景1. Introduction 常用基础理论知识2. The quadratic assignment problem3. Taboo search3.1. Moves3.2 Taboo list3.3. Aspiration function3.4. Taboo list size4. Random problems5. Parallel taboo search 研究内容、成果7. Conclusion 潜在…...
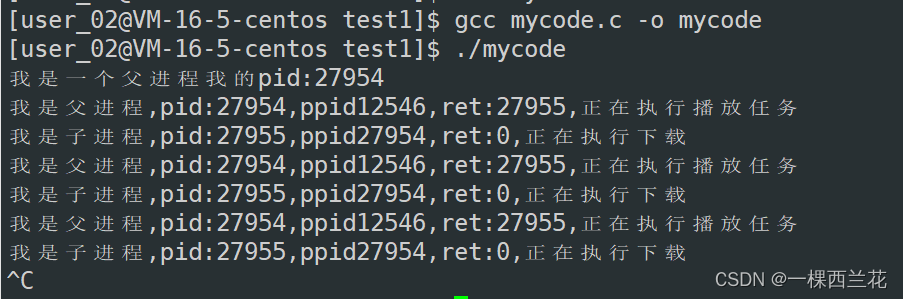
Linux:创建进程 -- fork,到底是什么?
相信大家在初学进程时,对fork函数创建进程一定会有很多的困惑,比如: 1.fork做了什么事情?? 2.为什么fork函数会有两个返回值?3.为什么fork的两个返回值,会给父进程谅回子进程pid,给子进程返回0?4.fork之后:父子进…...

基于SpringBoot+vue的token验证
后端: 1,写一个验证token的拦截器 import com.fasterxml.jackson.databind.ObjectMapper; import com.ffyc.news.model.CommonData; import org.springframework.web.servlet.HandlerInterceptor;import javax.servlet.http.HttpServletRequest; impor…...

Clickhouse设置多磁盘存储策略
设置多磁盘存储 clickhouse安装完成以后,配置了一个默认的存储空间, 这个只能配置一个目录,如果要使用多个磁盘目录,则需要配置磁盘组策略 查看当前的存储策略 select name, path, formatReadableSize(free_space) as free, fo…...
Python开发运维:Django 4.2.7 使用Celery 5.3.5 完成异步和定时任务
目录 一、实验 1.Django使用Celery完成异步和定时任务 二、问题 1. 如何查看Django版本 一、实验 1.Django使用Celery完成异步和定时任务 (1)安装Django (2)新建Django项目 (3)初始框架 (4)urls.py引用视图views from django.contrib import admin from django.urls imp…...

媒体增加日活量的有效策略
随着数字媒体的蓬勃发展,提高日活量成为媒体平台追求的重要目标之一。日活量的增加不仅意味着更广泛的影响力,还能为媒体平台带来更多的商业机会。以下是一些有效的策略,可帮助媒体提高日活量: admaoyan猫眼聚合 内容优质化&#…...

es6新特性总结
1、支持了let和const,为了防止var声明变量带来的变量提升 (1)、存在块级作用域不存在变量提升(考虑暂时性死区) (2)、不允许重复声明(包括普通变量和函数参数)变量提升…...

Spring Boot + hutool 创建海报图片
Spring Boot hutool 创建海报图片 /*** 分享,生成图片* param id* return*/GetMapping("/getShareImg")public void getShareImg(String id,HttpServletResponse response) throws IOException {CouponConsignSaleClassify byId couponConsignSaleClassifyService…...
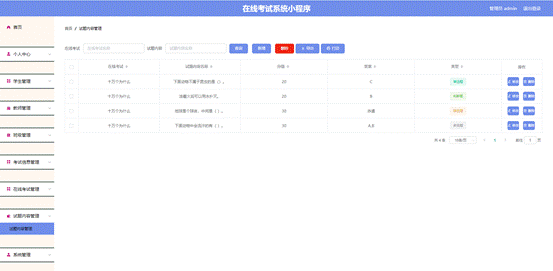
0002Java程序设计-springboot在线考试系统小程序
文章目录 **摘 要****目录**系统实现开发环境 编程技术交流、源码分享、模板分享、网课分享 企鹅🐧裙:776871563 摘 要 本毕业设计的内容是设计并且实现一个基于springboot的在线考试系统小程序。它是在Windows下,以MYSQL为数据库开发平台&…...
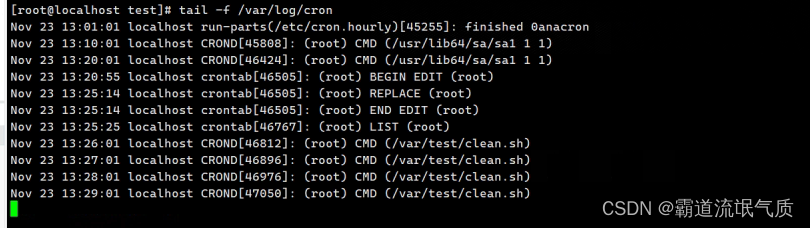
Linux(Centos)上使用crontab实现定时任务(定时执行脚本)
场景 Windows中通过bat定时执行命令和mysqldump实现数据库备份: Windows中通过bat定时执行命令和mysqldump实现数据库备份_mysqldump bat-CSDN博客 上面讲windows中使用bat实现定时任务的方式,如果是在linux上可以通过crontab实现。 cron是服务名称。…...

【Leetcode合集】20. 有效的括号
20. 有效的括号 20. 有效的括号 代码仓库地址: https://github.com/slience-me/Leetcode 个人博客 :https://slienceme.xyz 给定一个只包括 (,),{,},[,] 的字符串 s ,判断字符串…...
)
OpenGL 绘制线(Qt)
文章目录 一、简介二、实现代码三、实现效果参考资料一、简介 这里同样对OpenGL中的绘制线操作进行封装,便于后续的操作,很多形状也都是基于线来生成的,如圆形等。 二、实现代码 LineDrawable.h #ifndef LINE_DRAWABLE_H #define LINE_DRAWABLE_H#include...

Java | 多线程并发编程CountDownLatch实践
关注:CodingTechWork 引言 在一次数据割接需求中,数据需要通过编程的方式进行转移割接到新平台,此时若串行化方式,无疑会拉锯此次战斗,所以首当其冲要使用并发编程来降低割接时长。 本次主要考虑使用CountDownLatc…...

分布式定时任务系列6:XXL-job触发日志过大引发的CPU告警
传送门 分布式定时任务系列1:XXL-job安装 分布式定时任务系列2:XXL-job使用 分布式定时任务系列3:任务执行引擎设计 分布式定时任务系列4:任务执行引擎设计续 分布式定时任务系列5:XXL-job中blockingQueue的应用 …...

Spark RDD、DataFrame和Dataset的区别和联系
一、三种数据介绍 是Spark中的三种不同的数据结构,它们都可以用于分布式数据处理,但是它们的实现方式和使用方法略有不同。 RDD(弹性分布式数据集) RDD是Spark最初的核心数据结构,它是一个分布式的、只读的、可容错的…...
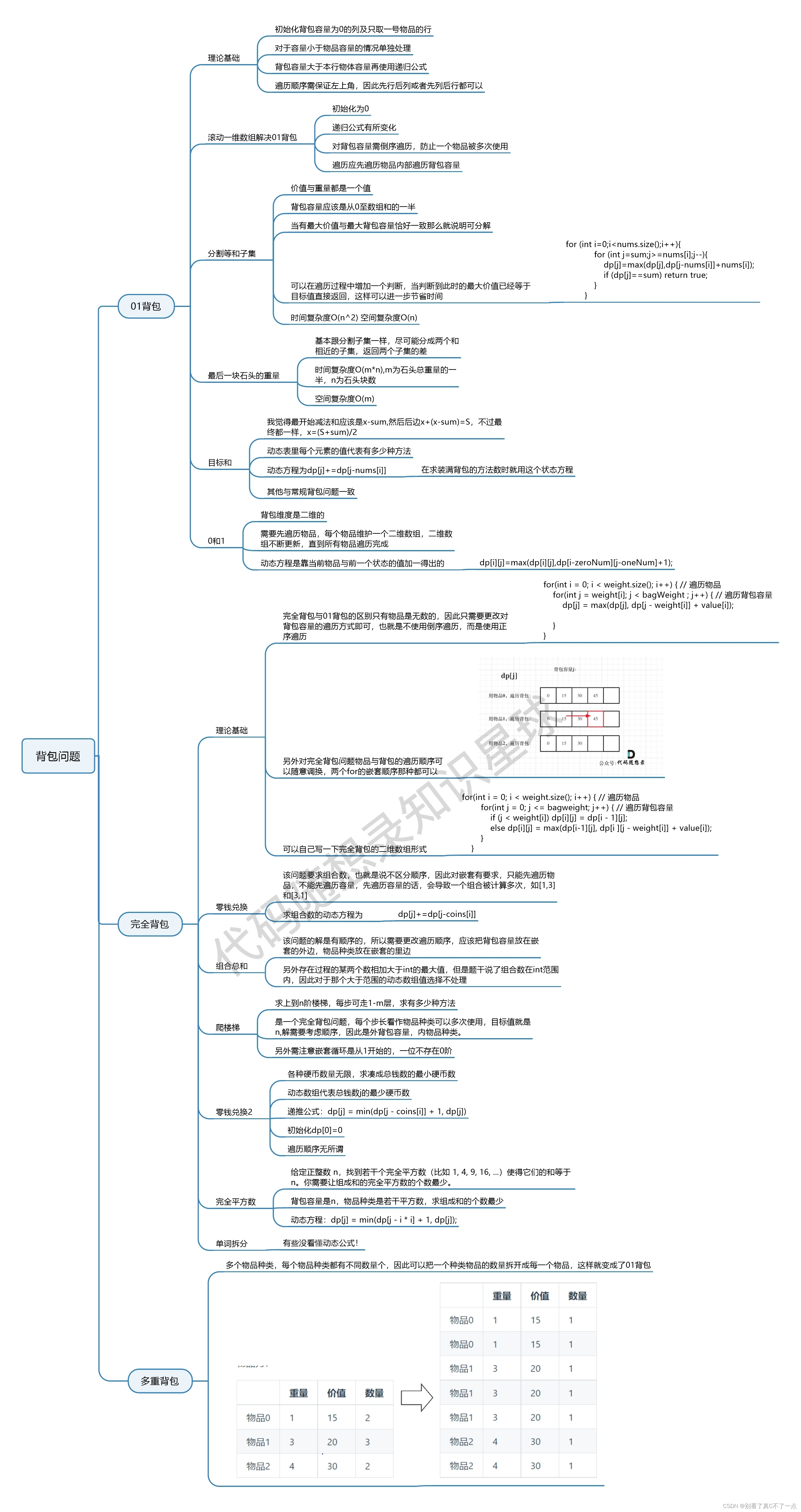
代码随想录算法训练营第四十五天|139.单词拆分、背包问题总结
LeetCode 139. 单词拆分 题目链接:139. 单词拆分 - 力扣(LeetCode) 这道题使用完全背包来实现,我们首先考虑字符串是否可以由字符串列表组成,因此dp数组大小为n 1 ,其意义是,在n个位置时是否能…...

深度学习卫星遥感图像检测与识别 -opencv python 目标检测 计算机竞赛
文章目录 0 前言1 课题背景2 实现效果3 Yolov5算法4 数据处理和训练5 最后 0 前言 🔥 优质竞赛项目系列,今天要分享的是 🚩 **深度学习卫星遥感图像检测与识别 ** 该项目较为新颖,适合作为竞赛课题方向,学长非常推荐…...

wxWidgets 3.2.4发布 —— 发布于2023年11月11日
稳定的3.2系列中的另一个版本现在可以在GitHub上获得。您可以在那里找到包含库源代码和文档的归档文件,以及所选Windows编译器(如Microsoft Visual C、MinGW-w64和TDM-GCC)的二进制文件。您还可以阅读此版本的更新文档,特别是&…...
PyQt6运行QTDesigner生成的ui文件程序
2024版 PyQt6 Python桌面开发 视频教程(无废话版) 玩命更新中~_哔哩哔哩_bilibili2024版 PyQt6 Python桌面开发 视频教程(无废话版) 玩命更新中~共计18条视频,包括:2024版 PyQt6 Python桌面开发 视频教程(无废话版) 玩命更新中~、第2讲 PyQt6库和工具库Q…...

基于mediapipe的人手21点姿态检测模型—CPU上检测速度惊人
前期的文章,我们介绍了MediaPipe对象检测与对象分类任务,也分享了MediaPipe的人手手势识别。在进行人手手势识别前,MediaPipe首先需要进行人手的检测与人手坐标点的检测,经过以上的检测后,才能把人手的坐标点与手势结合起来,进行相关的手势识别。 MediaPipe人手坐标点检测…...

XML Group端口详解
在XML数据映射过程中,经常需要对数据进行分组聚合操作。例如,当处理包含多个物料明细的XML文件时,可能需要将相同物料号的明细归为一组,或对相同物料号的数量进行求和计算。传统实现方式通常需要编写脚本代码,增加了开…...

接口测试中缓存处理策略
在接口测试中,缓存处理策略是一个关键环节,直接影响测试结果的准确性和可靠性。合理的缓存处理策略能够确保测试环境的一致性,避免因缓存数据导致的测试偏差。以下是接口测试中常见的缓存处理策略及其详细说明: 一、缓存处理的核…...

YSYX学习记录(八)
C语言,练习0: 先创建一个文件夹,我用的是物理机: 安装build-essential 练习1: 我注释掉了 #include <stdio.h> 出现下面错误 在你的文本编辑器中打开ex1文件,随机修改或删除一部分,之后…...

el-switch文字内置
el-switch文字内置 效果 vue <div style"color:#ffffff;font-size:14px;float:left;margin-bottom:5px;margin-right:5px;">自动加载</div> <el-switch v-model"value" active-color"#3E99FB" inactive-color"#DCDFE6"…...

第25节 Node.js 断言测试
Node.js的assert模块主要用于编写程序的单元测试时使用,通过断言可以提早发现和排查出错误。 稳定性: 5 - 锁定 这个模块可用于应用的单元测试,通过 require(assert) 可以使用这个模块。 assert.fail(actual, expected, message, operator) 使用参数…...

vue3 定时器-定义全局方法 vue+ts
1.创建ts文件 路径:src/utils/timer.ts 完整代码: import { onUnmounted } from vuetype TimerCallback (...args: any[]) > voidexport function useGlobalTimer() {const timers: Map<number, NodeJS.Timeout> new Map()// 创建定时器con…...

【python异步多线程】异步多线程爬虫代码示例
claude生成的python多线程、异步代码示例,模拟20个网页的爬取,每个网页假设要0.5-2秒完成。 代码 Python多线程爬虫教程 核心概念 多线程:允许程序同时执行多个任务,提高IO密集型任务(如网络请求)的效率…...

3403. 从盒子中找出字典序最大的字符串 I
3403. 从盒子中找出字典序最大的字符串 I 题目链接:3403. 从盒子中找出字典序最大的字符串 I 代码如下: class Solution { public:string answerString(string word, int numFriends) {if (numFriends 1) {return word;}string res;for (int i 0;i &…...
:观察者模式)
JS设计模式(4):观察者模式
JS设计模式(4):观察者模式 一、引入 在开发中,我们经常会遇到这样的场景:一个对象的状态变化需要自动通知其他对象,比如: 电商平台中,商品库存变化时需要通知所有订阅该商品的用户;新闻网站中࿰…...

SpringAI实战:ChatModel智能对话全解
一、引言:Spring AI 与 Chat Model 的核心价值 🚀 在 Java 生态中集成大模型能力,Spring AI 提供了高效的解决方案 🤖。其中 Chat Model 作为核心交互组件,通过标准化接口简化了与大语言模型(LLM࿰…...
