YOLOV7主干改进,使用fasternet轻量化改进主干(完整教程)
1,Pconv(来自Fasternet)(可作为模型中的基础卷积模块使用)
论文链接:https://arxiv.org/abs/2303.03667

2,为了大家方便的使用,这里我对原本的PConv的代码做了部分的改动,使得它的参数设置与Conv保持一致。大家直接将这一部分代码放到models/common.py的最后面。
import torch
import torch.nn as nn
import torch.nn.functional as F
class PConv(nn.Module):def __init__(self,dim: int,c2,k,s=1,n_div=2,forward: str = "split_cat",kernel_size: int = 3) -> None:super(PConv, self).__init__()self.dim_conv = dim//n_divself.dim_untouched = dim - self.dim_convself.conv = nn.Conv2d(self.dim_conv,self.dim_conv,kernel_size=k,stride=s,padding=k//2,bias=False)self.bn = nn.BatchNorm2d(dim)self.act = nn.SiLU()def forward(self,x):x1,x2 = torch.split(x,[self.dim_conv,self.dim_untouched],dim=1)x1 = self.conv(x1)x = torch.cat((x1,x2),1)return self.act(self.bn(x))3,在models/yolo.py中将模块名添加上,大约是752行
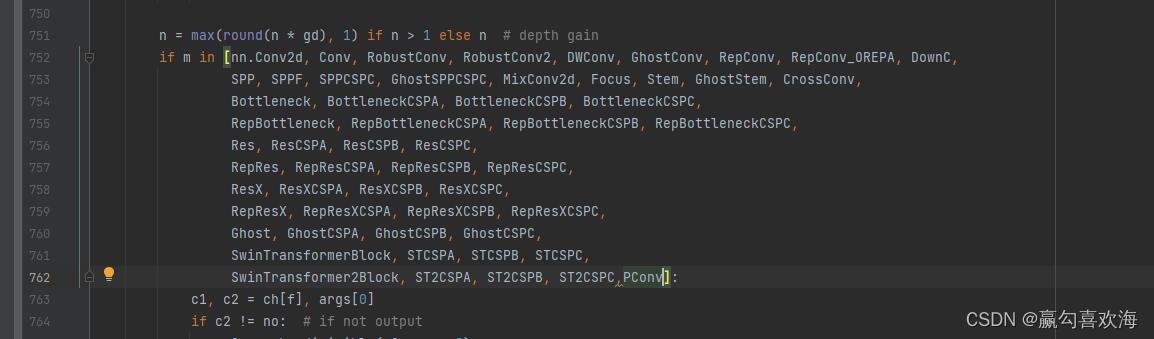
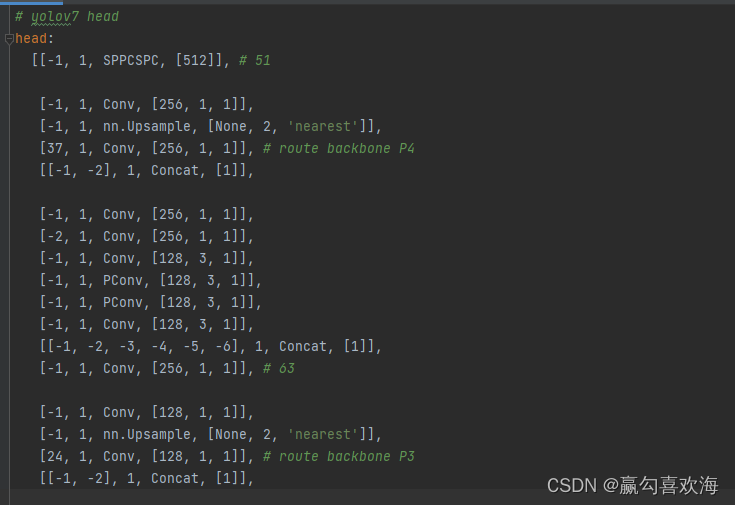
4,自己动手diy配置文件yolov7.yaml文件。
这里有一个注意事项,因为PConv本身只是一个基本的卷积操作,因此它并不支持下采样和通道变换操作,因此为了尽可能的简单,大家直接在一些通道前后没改变的地方,没有进行下采样的地方使用PConv即可。
相关文章:

YOLOV7主干改进,使用fasternet轻量化改进主干(完整教程)
1,Pconv(来自Fasternet)(可作为模型中的基础卷积模块使用) 论文链接:https://arxiv.org/abs/2303.03667 2,为了大家方便的使用,这里我对原本的PConv的代码做了部分的改动࿰…...
DALSA.SaperaLT.SapClassBasic无法加载,试图加载格式不正确的程序,c#
情景:用c#wpf写DALSA线扫相机的项目,生成时不报错,运行到DALSA相关的代码就报错找不到dll(DALSA的技术支持没给到任何支持 ) 一.根据框架选择dll 如果是.net framework框架(比如说.net480)&am…...
设计模式-创建型模式-工厂方法模式
一、什么是工厂方法模式 工厂模式又称工厂方法模式,是一种创建型设计模式,其在父类中提供一个创建对象的方法, 允许子类决定实例化对象的类型。工厂方法模式是目标是定义一个创建产品对象的工厂接口,将实际创建工作推迟到子类中。…...
科研/比赛必备工具及系列笔记集合
科研/比赛必备工具及系列笔记集合 零、前言一、常用工具系列1.1 笔记平台使用感受系列1.2 常用开发平台系列 二、论文系列2.1 检索工具系列2.2 投稿调研系列2.3 常见国际期刊/会议2.4 常见中文核心期刊/会议 三、文献系列3.1 画图工具系列3.2 翻译工具系列3.3 英文纠正系列3.4 …...

萨科微举办工作交流和业务分享会
萨科微(www.slkoric.com)举办工作交流和业务分享会,狠抓人才培养团队的基本功建设。萨科微总经理宋仕强先生认为,当下市场经济形势复杂多变,给公司经营带来巨大压力,同时考验着企业自身的发展韧性。萨科微公…...

一篇文章让你入门python集合和字典
嗨喽~大家好呀,这里是魔王呐 ❤ ~! python更多源码/资料/解答/教程等 点击此处跳转文末名片免费获取 一、集合: 增加 add 删除 del 删除集合 discard(常用)删除集合中的元素 ,删除一个不存在的元素不会报错 remove 删除一个不存在的元素会报错 pop随…...
各种工具的快捷键或命令
前言 这里就存放自己存有的一些小工具的地址以及工具的命令。 正文 零、各种小工具 1、wizTree:磁盘分析工具-分析磁盘的文件夹存储 2、稻壳阅读器:有黑色背景 3、youtube 视频下载:https://zh.savefrom.net/226/ 4、视频录制:Bandica…...

【Web】preg_match绕过相关例题wp
目录 ①[FBCTF 2019]rceservice ②[ctfshow]web130 ③[ctfshow]web131 ④[NISACTF 2022]middlerce 简单回顾一下基础 参考文章 p牛神文 preg_match绕过总的来讲就三块可利用 数组绕过、PCRE回溯次数限制、换行符 ①[FBCTF 2019]rceservice 先贴出附件给的源码 &l…...
)
XSLVGL2.0 User Manual 主题管理器(v2.0)
XSLVGL2.0 开发手册 XSLVGL2.0 Brief 1、概述2、特性3、APIs3.1、xs_page_theme_register3.2、xs_page_get_theme_current3.3、xs_page_set_theme_current3.4、xs_page_get_theme_count3.5、xs_page_get_theme_id3.6、xs_page_get_theme_name3.7、xs_page_get_theme4、使用方法…...

visionOS空间计算实战开发教程Day 2 使用RealityKit显示3D素材
我们在Day1中学习了如何创建一个visionOS应用,但在第一个Demo应用中我们的界面内容还是2D的,看起来和其它应用并没有什么区别。接下来我们先学习如何展示3D素材,苹果为方便开发人员,推出了RealityKit,接下来看…...

【图解系列】一张图带你了解 DevOps 生态工具
一张图带你了解 DevOps 生态工具 ✅ 协作(Collaborate):JIRA、Confluence 大家肯定不陌生了,我之前也写过利用 Jekyll 搭建个人博客的帖子。✅ 构建(Build):常用的 SCM(Software Con…...

Oracle的安装及使用流程
Oracle的安装及使用流程 1.Win10安装Oracle10g 1.1 安装与测试 安装版本: OracleXEUniv10.2.1015.exe 步骤参考:oracleXe下载与安装 安装完成后测试是否正常 # 输入命令连接oracle conn sys as sysdba; # 无密码,直接按回车 # 测试连接的s…...

CMakeLists.txt:打印find_package变量;判断库文件路径设定是否正确;install文件设置
CMake打印find_package变量;install文件设置 打印find_package找到的各种变量判断库文件是否被找到install文件设置install详细说明 打印find_package找到的各种变量 目的:find_package后,想使用找到的include/lib文件夹。 find_package(Yo…...

Mysql 解决Invalid default value for ‘created_at‘
在mysql版本 8.0 和 5.* 之间数据互导的过程中,老是会出现各种错误,比如 这个created_at 一定要有一个默认值, 但是我加了 default null 还是会报错,于是对照了其他的DDL 发现,需要再加 null default null 才行&#…...

Linux【安全 01】云服务器主机安全加固(修改SSHD端口、禁用登陆失败的IP地址、使用密钥登录)
云服务器主机安全加固 1.SSH登录尝试的系统日志信息2.安全加固方法2.1 修改SSHD端口2.2 禁用登陆失败的IP地址2.3 使用密钥登录 3.总结 1.SSH登录尝试的系统日志信息 Last failed login: Sat Oct 7 14:10:39 CST 2023 from xxx.xx.xx.xxx on ssh:notty There were 10 failed …...
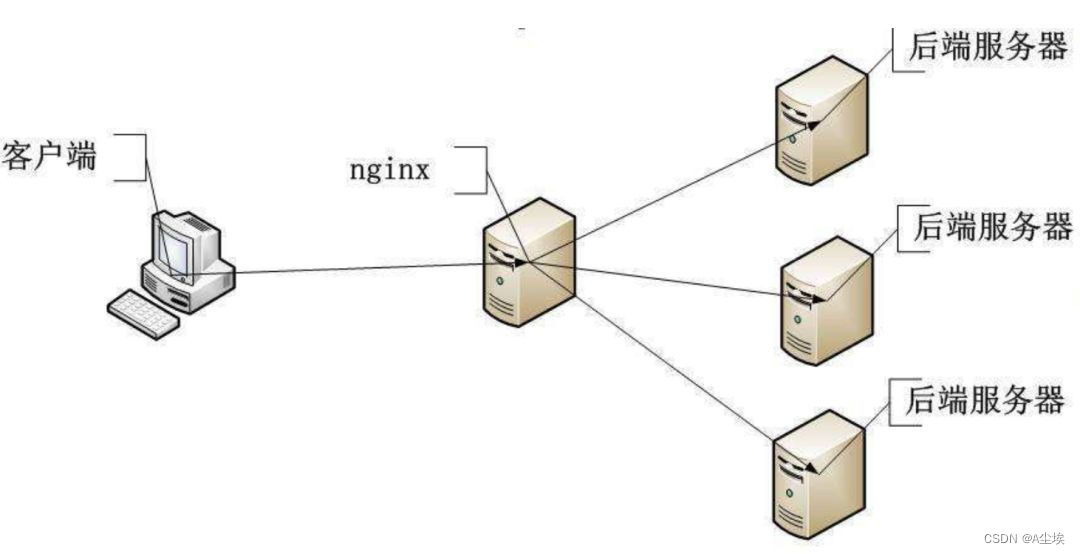
nginx的n种用法(nginx安装+正向代理+反向代理+透明代理+负载均衡+静态服务器)
nginx的安装 一、安装依赖 # 一键安装四个依赖 yum -y install gcc zlib zlib-devel pcre-devel openssl openssl-devel二、安装nginx yum install nginx三、检查是否安装成功 nginx -v四、启动/停止nginx /etc/init.d/nginx start /etc/init.d/nginx stop五、编辑配置文件…...
lvm 扩容根分区失败记录
lvm 扩容根分区失败记录 1、问题描述2、错误描述3、解决方法重启系统进入grub界面,选择kernel 2.x 启动系统。然后同样的resize2fs命令扩容成功。 1、问题描述 根分区不足。 系统有2个内核版本,一个是kernel 2.x,另一个是kernel 4.x。 这次l…...
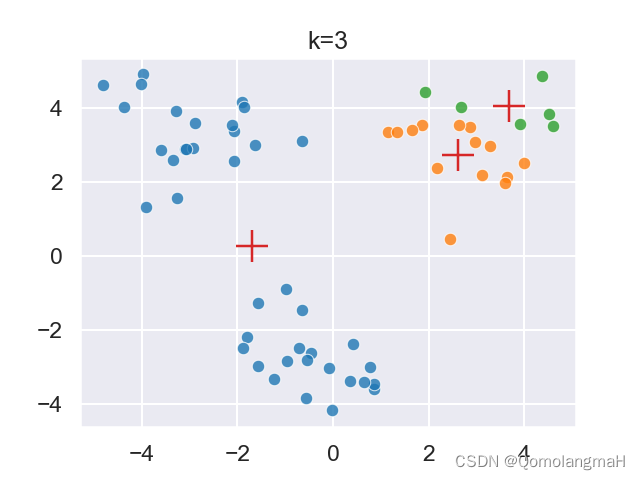
【机器学习】聚类(一):原型聚类:K-means聚类
文章目录 一、实验介绍1. 算法流程2. 算法解释3. 算法特点4. 应用场景5. 注意事项 二、实验环境1. 配置虚拟环境2. 库版本介绍 三、实验内容0. 导入必要的库1. Kmeans类a. 构造函数b. 闵可夫斯基距离c. 初始化簇心d. K-means聚类e. 聚类结果可视化 2. 辅助函数3. 主函数a. 命令…...

2824. 统计和小于目标的下标对数目 --力扣 --JAVA
题目 给你一个下标从 0 开始长度为 n 的整数数组 nums 和一个整数 target ,请你返回满足 0 < i < j < n 且 nums[i] nums[j] < target 的下标对 (i, j) 的数目。 解题思路 对数组进行排序,可以利用List自带的sort函数传递比较规则(代码中的…...
github上不去
想要网上找代码发现github上不去了 发现之前的fastgit也用不了了 搜了很多地方终于找到了 记录保存一下 fastgithub最新下载 选择第二个下载解压就行 使用成功!...

React19源码系列之 事件插件系统
事件类别 事件类型 定义 文档 Event Event 接口表示在 EventTarget 上出现的事件。 Event - Web API | MDN UIEvent UIEvent 接口表示简单的用户界面事件。 UIEvent - Web API | MDN KeyboardEvent KeyboardEvent 对象描述了用户与键盘的交互。 KeyboardEvent - Web…...

ESP32 I2S音频总线学习笔记(四): INMP441采集音频并实时播放
简介 前面两期文章我们介绍了I2S的读取和写入,一个是通过INMP441麦克风模块采集音频,一个是通过PCM5102A模块播放音频,那如果我们将两者结合起来,将麦克风采集到的音频通过PCM5102A播放,是不是就可以做一个扩音器了呢…...

Robots.txt 文件
什么是robots.txt? robots.txt 是一个位于网站根目录下的文本文件(如:https://example.com/robots.txt),它用于指导网络爬虫(如搜索引擎的蜘蛛程序)如何抓取该网站的内容。这个文件遵循 Robots…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个生活电费的缴纳和查询小程序
一、项目初始化与配置 1. 创建项目 ohpm init harmony/utility-payment-app 2. 配置权限 // module.json5 {"requestPermissions": [{"name": "ohos.permission.INTERNET"},{"name": "ohos.permission.GET_NETWORK_INFO"…...
)
GitHub 趋势日报 (2025年06月08日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 884 cognee 566 dify 414 HumanSystemOptimization 414 omni-tools 321 note-gen …...

LLM基础1_语言模型如何处理文本
基于GitHub项目:https://github.com/datawhalechina/llms-from-scratch-cn 工具介绍 tiktoken:OpenAI开发的专业"分词器" torch:Facebook开发的强力计算引擎,相当于超级计算器 理解词嵌入:给词语画"…...

MySQL 8.0 OCP 英文题库解析(十三)
Oracle 为庆祝 MySQL 30 周年,截止到 2025.07.31 之前。所有人均可以免费考取原价245美元的MySQL OCP 认证。 从今天开始,将英文题库免费公布出来,并进行解析,帮助大家在一个月之内轻松通过OCP认证。 本期公布试题111~120 试题1…...

ArcGIS Pro制作水平横向图例+多级标注
今天介绍下载ArcGIS Pro中如何设置水平横向图例。 之前我们介绍了ArcGIS的横向图例制作:ArcGIS横向、多列图例、顺序重排、符号居中、批量更改图例符号等等(ArcGIS出图图例8大技巧),那这次我们看看ArcGIS Pro如何更加快捷的操作。…...

LLMs 系列实操科普(1)
写在前面: 本期内容我们继续 Andrej Karpathy 的《How I use LLMs》讲座内容,原视频时长 ~130 分钟,以实操演示主流的一些 LLMs 的使用,由于涉及到实操,实际上并不适合以文字整理,但还是决定尽量整理一份笔…...

站群服务器的应用场景都有哪些?
站群服务器主要是为了多个网站的托管和管理所设计的,可以通过集中管理和高效资源的分配,来支持多个独立的网站同时运行,让每一个网站都可以分配到独立的IP地址,避免出现IP关联的风险,用户还可以通过控制面板进行管理功…...
