【机器学习】聚类(三):原型聚类:高斯混合聚类
文章目录
- 一、实验介绍
- 1. 算法流程
- 2. 算法解释
- 3. 算法特点
- 4. 应用场景
- 5. 注意事项
- 二、实验环境
- 1. 配置虚拟环境
- 2. 库版本介绍
- 三、实验内容
- 0. 导入必要的库
- 1. 全局调试变量
- 2. 调试函数
- 3. 高斯密度函数(phi)
- 4. E步(getExpectation)
- 5. M步(maximize)
- 6. 数据缩放函数
- 7. 初始化参数
- 8. GMM EM算法函数
- 9. 主函数
- 四、代码整合
高斯混合聚类是一种基于概率模型的聚类方法,采用多个高斯分布的线性组合来表示数据的聚类结构。通过对每个样本的多个高斯分布进行加权组合,该算法能够更灵活地适应不同形状的聚类。
一、实验介绍
1. 算法流程
- 初始化:
初始化高斯混合分布的模型参数,包括每个高斯混合成分的均值向量 μ i \mu_i μi、协方差矩阵 Σ i \Sigma_i Σi 和混合系数 π i \pi_i πi。
{ ( μ 1 , Σ 1 , π 1 ) , ( μ 2 , Σ 2 , π 2 ) , . . . , ( μ k , Σ k , π k ) } \{(\mu_1, \Sigma_1, \pi_1), (\mu_2, \Sigma_2, \pi_2), ..., (\mu_k, \Sigma_k, \pi_k)\} {(μ1,Σ1,π1),(μ2,Σ2,π2),...,(μk,Σk,πk)}
-
迭代过程(EM算法):
- Expectation (E) 步骤:
对于每个样本 X j X_j Xj 计算其由各混合成分生成的后验概率 γ i j \gamma_{ij} γij,表示样本属于第 i i i 个混合成分的概率。
γ i j = π i ⋅ N ( X j ∣ μ i , Σ i ) ∑ l = 1 k π l ⋅ N ( X j ∣ μ l , Σ l ) \gamma_{ij} = \frac{\pi_i \cdot \mathcal{N}(X_j | \mu_i, \Sigma_i)}{\sum_{l=1}^{k} \pi_l \cdot \mathcal{N}(X_j | \mu_l, \Sigma_l)} γij=∑l=1kπl⋅N(Xj∣μl,Σl)πi⋅N(Xj∣μi,Σi)
- Maximization (M) 步骤:
更新模型参数:- 新均值向量 μ i \mu_i μi 的更新: μ i = ∑ j = 1 m γ i j X j ∑ j = 1 m γ i j \mu_i = \frac{\sum_{j=1}^{m} \gamma_{ij} X_j}{\sum_{j=1}^{m} \gamma_{ij}} μi=∑j=1mγij∑j=1mγijXj
- 新协方差矩阵 Σ i \Sigma_i Σi 的更新: Σ i = ∑ j = 1 m γ i j ( X j − μ i ) ( X j − μ i ) T ∑ j = 1 m γ i j \Sigma_i = \frac{\sum_{j=1}^{m} \gamma_{ij} (X_j - \mu_i)(X_j - \mu_i)^T}{\sum_{j=1}^{m} \gamma_{ij}} Σi=∑j=1mγij∑j=1mγij(Xj−μi)(Xj−μi)T
- 新混合系数 π i \pi_i πi 的更新: π i = 1 m ∑ j = 1 m γ i j \pi_i = \frac{1}{m} \sum_{j=1}^{m} \gamma_{ij} πi=m1∑j=1mγij
- Expectation (E) 步骤:
-
停止条件:
根据设定的停止条件,比如达到最大迭代轮数或模型参数的变化小于某一阈值。 -
簇划分:
根据得到的后验概率 γ i j \gamma_{ij} γij 确定每个样本的簇标记,将样本划入概率最大的簇中。C i = { X j ∣ argmax i γ i j , 1 ≤ i ≤ k } C_i = \{X_j | \text{argmax}_i \gamma_{ij}, 1 \leq i \leq k\} Ci={Xj∣argmaxiγij,1≤i≤k}
-
输出:
返回最终的簇划分 C = { C 1 , C 2 , . . . , C k } C = \{C_1, C_2, ..., C_k\} C={C1,C2,...,Ck}。
高斯混合聚类采用了迭代优化的方式,通过不断更新均值向量、协方差矩阵和混合系数,使得模型对数据的拟合更好。EM算法的E步骤计算后验概率,M步骤更新模型参数,整个过程不断迭代直至满足停止条件。最后,将每个样本划分到概率最大的簇中。
2. 算法解释
- 通过EM算法的E步骤,计算每个样本属于每个混合成分的后验概率。
- 通过EM算法的M步骤,更新每个混合成分的均值向量、协方差矩阵和混合系数,优化模型对数据的拟合。
- 算法通过迭代过程,不断调整模型参数,使得混合分布更好地刻画数据的分布。
3. 算法特点
- 通过多个高斯分布的组合,适用于不同形状的聚类结构。
- 采用EM算法进行迭代优化,灵活适应数据的复杂分布。
4. 应用场景
- 适用于数据具有多个分布的情况,且每个分布可以用高斯分布来描述。
- 在图像分割、语音识别等领域广泛应用。
5. 注意事项
- 初始参数的选择可能影响最终聚类效果,因此需要进行多次运行选择最优结果。
- 算法对异常值不敏感,但在特定场景下可能需要考虑异常值的处理。
二、实验环境
1. 配置虚拟环境
conda create -n ML python==3.9
conda activate ML
conda install scikit-learn matplotlib
2. 库版本介绍
| 软件包 | 本实验版本 |
|---|---|
| matplotlib | 3.5.2 |
| numpy | 1.21.5 |
| python | 3.9.13 |
| scikit-learn | 1.0.2 |
三、实验内容
0. 导入必要的库
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import multivariate_normal
from sklearn.datasets import load_iris
1. 全局调试变量
DEBUG = True
- 该变量控制是否在执行过程中打印调试信息。
2. 调试函数
def debug(*args, **kwargs):global DEBUGif DEBUG:print(*args, **kwargs)
- 用于打印调试信息的函数。在整个代码中都使用了它以进行调试。
3. 高斯密度函数(phi)
def phi(Y, mu_k, cov_k):# Check for and handle infinite or NaN values in Ynorm = multivariate_normal(mean=mu_k, cov=cov_k)return norm.pdf(Y)
- 计算多元高斯分布的概率密度函数。
4. E步(getExpectation)
def getExpectation(Y, mu, cov, alpha):N = Y.shape[0]K = alpha.shape[0]assert N > 1, "There must be more than one sample!"assert K > 1, "There must be more than one gaussian model!"gamma = np.mat(np.zeros((N, K)))prob = np.zeros((N, K))for k in range(K):prob[:, k] = phi(Y, mu[k], cov[k]) * alpha[k]prob = np.mat(prob)for k in range(K):gamma[:, k] = prob[:, k] / np.sum(prob, axis=1)return gamma
- EM算法的E步骤,计算每个数据点属于每个簇的概率。主要步骤包括:
- 初始化一个零矩阵
gamma用于存储响应度。 - 对于每个簇,计算每个数据点属于该簇的概率(通过
phi函数计算),然后乘以该簇的混合系数。 - 归一化概率以得到响应度矩阵
gamma。
- 初始化一个零矩阵
5. M步(maximize)
def maximize(Y, gamma):N, D = Y.shapeK = gamma.shape[1]mu = np.zeros((K, D))cov = []alpha = np.zeros(K)for k in range(K):Nk = np.sum(gamma[:, k])mu[k, :] = np.sum(np.multiply(Y, gamma[:, k]), axis=0) / Nkdiff = Y - mu[k]cov_k = np.dot(diff.T, np.multiply(diff, gamma[:, k])) / Nkcov_k += 1e-6 * np.identity(D) # Adding a small value to the diagonal for stabilitycov.append(cov_k)alpha[k] = Nk / Ncov = np.array(cov)return mu, cov, alpha- EM算法的M步骤,即更新模型参数,主要步骤包括:
- 初始化均值
mu、协方差矩阵列表cov和混合系数alpha。 - 对于每个簇,计算新的均值、协方差矩阵和混合系数。均值的更新是通过加权平均计算的,协方差矩阵的更新考虑了数据的权重(响应度),混合系数的更新是每个簇中数据点的权重之和。
- 初始化均值
6. 数据缩放函数
def scale_data(Y):for i in range(Y.shape[1]):max_ = Y[:, i].max()min_ = Y[:, i].min()Y[:, i] = (Y[:, i] - min_) / (max_ - min_)debug("Data scaled.")return Y
- 将数据集中的每个特征缩放到 [0, 1] 范围内。
7. 初始化参数
def init_params(shape, K):N, D = shapemu = np.random.rand(K, D)cov = np.array([np.eye(D)] * K)alpha = np.array([1.0 / K] * K)debug("Parameters initialized.")debug("mu:", mu, "cov:", cov, "alpha:", alpha, sep="\n")return mu, cov, alpha- 初始化GMM的参数(均值、协方差和混合系数)。
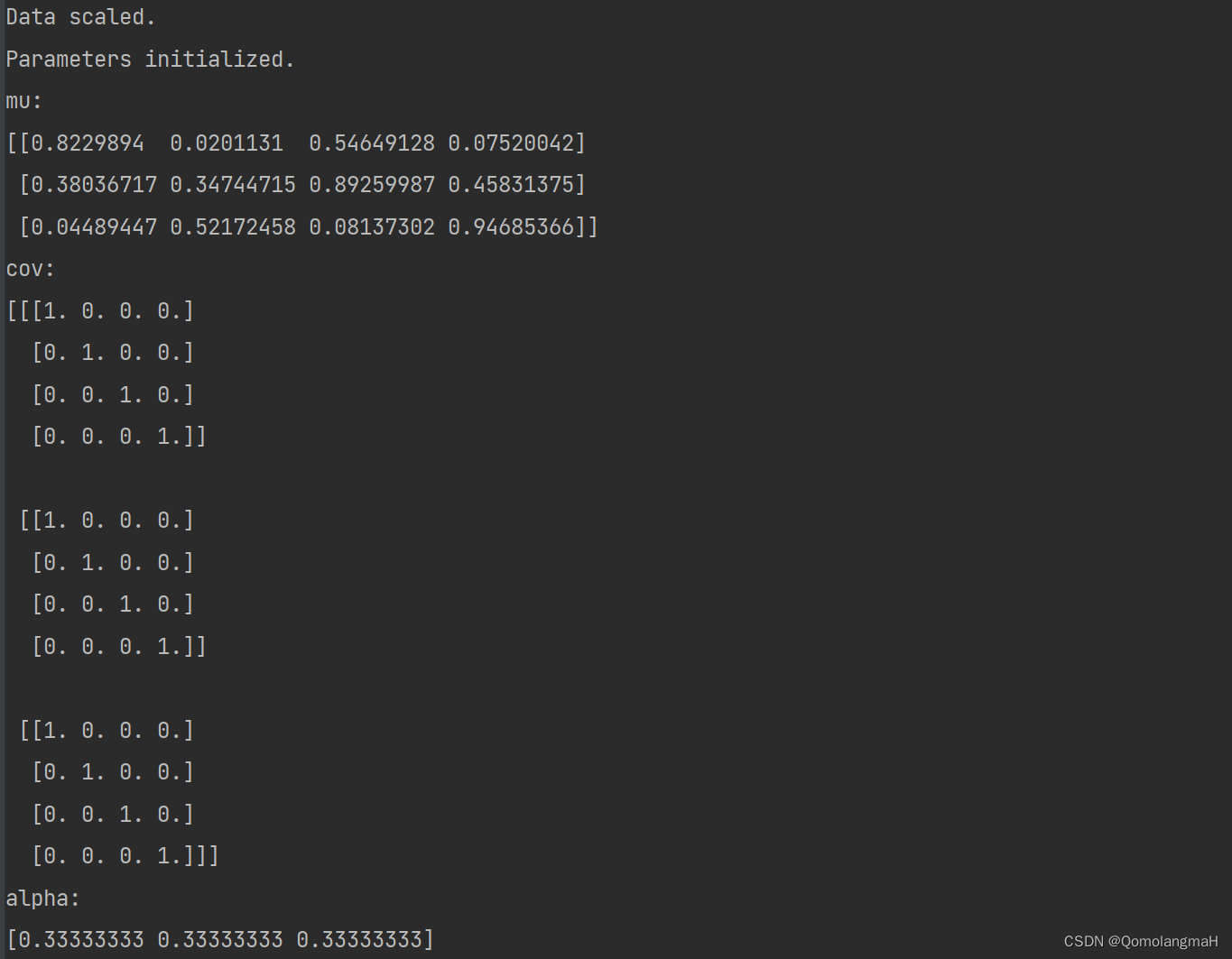
8. GMM EM算法函数
def GMM_EM(Y, K, times):Y = scale_data(Y)mu, cov, alpha = init_params(Y.shape, K)for i in range(times):gamma = getExpectation(Y, mu, cov, alpha)mu, cov, alpha = maximize(Y, gamma)debug("{sep} Result {sep}".format(sep="-" * 20))debug("mu:", mu, "cov:", cov, "alpha:", alpha, sep="\n")return mu, cov, alpha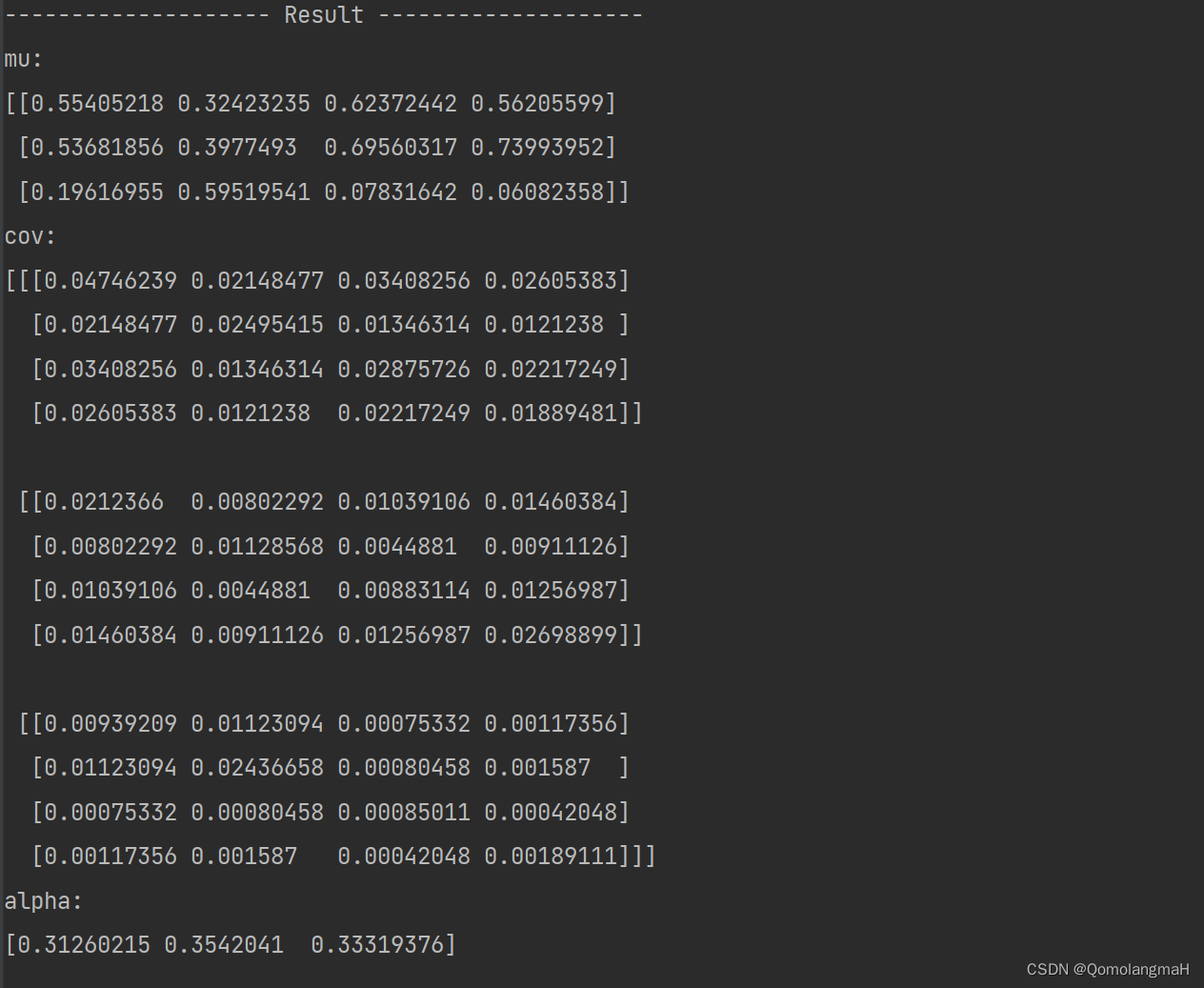
9. 主函数
if __name__ == '__main__':# Load Iris datasetiris = load_iris()Y = iris.data# Model parametersK = 3 # number of clustersiterations = 100# Run GMM EM algorithmmu, cov, alpha = GMM_EM(Y, K, iterations)# Clustering based on the trained modelN = Y.shape[0]gamma = getExpectation(Y, mu, cov, alpha)category = gamma.argmax(axis=1).flatten().tolist()[0]# Plotting the resultsfor i in range(K):cluster_data = np.array([Y[j] for j in range(N) if category[j] == i])plt.scatter(cluster_data[:, 0], cluster_data[:, 1], label=f'Cluster {i + 1}')plt.legend()plt.title("GMM Clustering By EM Algorithm")plt.xlabel("Feature 1")plt.ylabel("Feature 2")plt.show()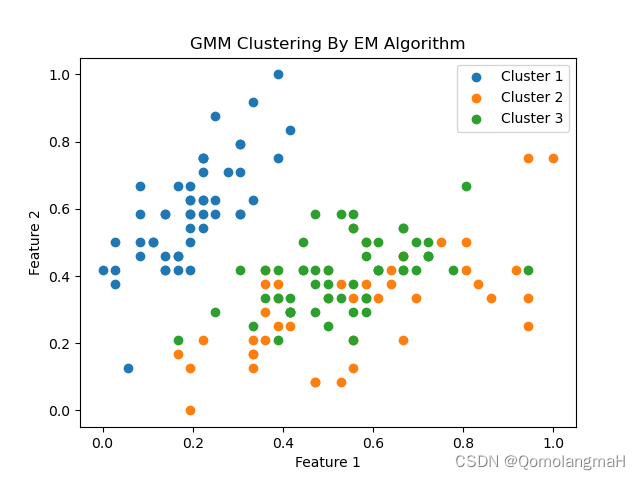
四、代码整合
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import multivariate_normal
from sklearn.datasets import load_irisDEBUG = Truedef debug(*args, **kwargs):global DEBUGif DEBUG:print(*args, **kwargs)def phi(Y, mu_k, cov_k):# Check for and handle infinite or NaN values in Ynorm = multivariate_normal(mean=mu_k, cov=cov_k)return norm.pdf(Y)def getExpectation(Y, mu, cov, alpha):N = Y.shape[0]K = alpha.shape[0]assert N > 1, "There must be more than one sample!"assert K > 1, "There must be more than one gaussian model!"gamma = np.mat(np.zeros((N, K)))prob = np.zeros((N, K))for k in range(K):prob[:, k] = phi(Y, mu[k], cov[k]) * alpha[k]prob = np.mat(prob)for k in range(K):gamma[:, k] = prob[:, k] / np.sum(prob, axis=1)return gammadef maximize(Y, gamma):N, D = Y.shapeK = gamma.shape[1]mu = np.zeros((K, D))cov = []alpha = np.zeros(K)for k in range(K):Nk = np.sum(gamma[:, k])mu[k, :] = np.sum(np.multiply(Y, gamma[:, k]), axis=0) / Nkdiff = Y - mu[k]cov_k = np.dot(diff.T, np.multiply(diff, gamma[:, k])) / Nkcov_k += 1e-6 * np.identity(D) # Adding a small value to the diagonal for stabilitycov.append(cov_k)alpha[k] = Nk / Ncov = np.array(cov)return mu, cov, alphadef scale_data(Y):for i in range(Y.shape[1]):max_ = Y[:, i].max()min_ = Y[:, i].min()Y[:, i] = (Y[:, i] - min_) / (max_ - min_)debug("Data scaled.")return Ydef init_params(shape, K):N, D = shapemu = np.random.rand(K, D)cov = np.array([np.eye(D)] * K)alpha = np.array([1.0 / K] * K)debug("Parameters initialized.")debug("mu:", mu, "cov:", cov, "alpha:", alpha, sep="\n")return mu, cov, alphadef GMM_EM(Y, K, times):Y = scale_data(Y)mu, cov, alpha = init_params(Y.shape, K)for i in range(times):gamma = getExpectation(Y, mu, cov, alpha)mu, cov, alpha = maximize(Y, gamma)debug("{sep} Result {sep}".format(sep="-" * 20))debug("mu:", mu, "cov:", cov, "alpha:", alpha, sep="\n")return mu, cov, alphaif __name__ == '__main__':# Load Iris datasetiris = load_iris()Y = iris.data# Model parametersK = 3 # number of clustersiterations = 100# Run GMM EM algorithmmu, cov, alpha = GMM_EM(Y, K, iterations)# Clustering based on the trained modelN = Y.shape[0]gamma = getExpectation(Y, mu, cov, alpha)category = gamma.argmax(axis=1).flatten().tolist()[0]# Plotting the resultsfor i in range(K):cluster_data = np.array([Y[j] for j in range(N) if category[j] == i])plt.scatter(cluster_data[:, 0], cluster_data[:, 1], label=f'Cluster {i + 1}')plt.legend()plt.title("GMM Clustering By EM Algorithm")plt.xlabel("Feature 1")plt.ylabel("Feature 2")plt.show()相关文章:

【机器学习】聚类(三):原型聚类:高斯混合聚类
文章目录 一、实验介绍1. 算法流程2. 算法解释3. 算法特点4. 应用场景5. 注意事项 二、实验环境1. 配置虚拟环境2. 库版本介绍 三、实验内容0. 导入必要的库1. 全局调试变量2. 调试函数3. 高斯密度函数(phi)4. E步(getExpectation)…...
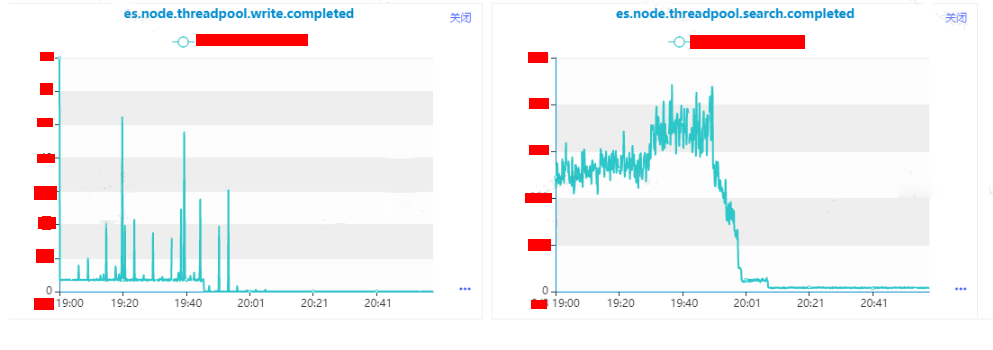
线上ES集群参数配置引起的业务异常案例分析
本文介绍了一次排查Elasticsearch node_concurrent_recoveries 引发的性能问题的过程。 一、故障描述 1.1 故障现象 1. 业务反馈 业务部分读请求抛出请求超时的错误。 2. 故障定位信息获取 故障开始时间 19:30左右开始 故障抛出异常日志 错误日志抛出timeout错误。 故障之前…...
【Docker】Docker 仓库管理和Docker Dockerfile
作者简介: 辭七七,目前大二,正在学习C/C,Java,Python等 作者主页: 七七的个人主页 文章收录专栏: 七七的闲谈 欢迎大家点赞 👍 收藏 ⭐ 加关注哦!💖…...

面试必问:如何快速定位BUG?BUG定位技巧及N板斧!
01 定位问题的重要性 很多测试人员可能会说,我的职责就是找到bug,至于找原因并修复,那是开发的事情,关我什么事? 好,我的回答是,如果您只想做一个测试人员最基本最本分的事情,那么可…...
力扣114. 二叉树展开为链表(java,用树模拟链表)
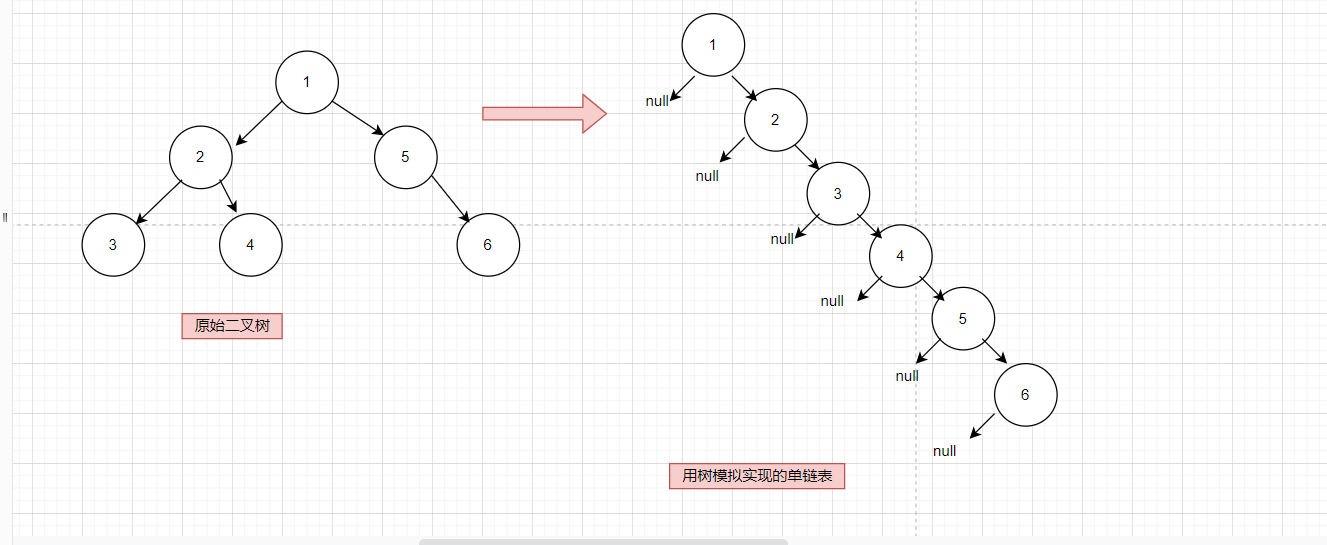
Problem: 114. 二叉树展开为链表 文章目录 题目描述思路解题方法复杂度Code 题目描述 给你二叉树的根结点 root ,请你将它展开为一个单链表: 1.展开后的单链表应该同样使用 TreeNode ,其中 right 子指针指向链表中下一个结点,而左…...
)
学生成绩管理系统(python实现)
学生成绩表信息包括学号、姓名、各科课程成绩(语文、数学、英语、政治)和总分。用带头结点的单链表管理学生成绩表,每个学生的信息依次从键盘输入,并根据需要进行插入、删除、排序、输出等操作。 import json# 初始化系统 studen…...

【Leetcode合集】1410. HTML 实体解析器
1410. HTML 实体解析器 1410. HTML 实体解析器 代码仓库地址: https://github.com/slience-me/Leetcode 个人博客 :https://slienceme.xyz 编写一个函数来查找字符串数组中的最长公共前缀。 如果不存在公共前缀,返回空字符串 ""…...

04-React脚手架 集成Axios
初始化React脚手架 前期准备 1.脚手架: 用来帮助程序员快速创建一个基于xxx库的模板项目 1.包含了所有需要的配置(语法检查、jsx编译、devServer…)2.下载好了所有相关的依赖3.可以直接运行一个简单效果 2.react提供了一个用于创建react项目的脚手架库…...

时序预测 | MATLAB实现基于BiLSTM-AdaBoost双向长短期记忆网络结合AdaBoost时间序列预测
时序预测 | MATLAB实现基于BiLSTM-AdaBoost双向长短期记忆网络结合AdaBoost时间序列预测 目录 时序预测 | MATLAB实现基于BiLSTM-AdaBoost双向长短期记忆网络结合AdaBoost时间序列预测预测效果基本介绍模型描述程序设计参考资料 预测效果 基本介绍 1.Matlab实现BiLSTM-Adaboost…...

【nlp】3.6 Tansformer模型构建(编码器与解码器模块耦合)
Tansformer模型构建(编码器与解码器模块耦合) 1. 模型构建介绍2 编码器-解码器结构的代码实现3 Tansformer模型构建过程的代码实现4 小结1. 模型构建介绍 通过上面的小节, 我们已经完成了所有组成部分的实现, 接下来就来实现完整的编码器-解码器结构耦合. Transformer总体架…...
【【Linux系统下常用指令学习 之 二 】】
Linux系统下常用指令学习 之 二 文件查询和搜索 文件的查询和搜索也是最常用的操作,在嵌入式 Linux 开发中常常需要在 Linux 源码文件中查询某个文件是否存在,或者搜索哪些文件都调用了某个函数等等。 1、命令 find find 命令用于在目录结构中查找文件…...

Git-将指定文件回退到指定版本
场景1:修改了文件/path/to/file,没有提交,但是觉得改的不好,想还原。 解决: git checkout -- /path/to/file 场景2:修改了文件/path/to/file,已经提交,但是觉得改的不好,…...

docker环境安装
环境 主机环境 1. 宿主机环境 ubuntu-22.04.3-live-server-amd64 ,下载地址: https://mirrors.aliyun.com/ubuntu-releases/22.04.3/ubuntu-22.04.3-live-server-amd64.iso 2. apt 包管理器,镜像源修改 : 将 http://cn.archive.ubunt…...

【Java】智慧工地云平台源码(APP+SaaS模式)
在谈论“智慧工地”之前,我们首先得知道传统工地为什么跟不上时代了。 说起传统工地,总有一些很突出的问题:比如工友多且杂,他们是否入场、身体状况如何,管理人员只能依靠巡查、手工纪录来判断,耗时耗力&am…...

2016年11月10日 Go生态洞察:七年的Go语言旅程
🌷🍁 博主猫头虎(🐅🐾)带您 Go to New World✨🍁 🦄 博客首页——🐅🐾猫头虎的博客🎐 🐳 《面试题大全专栏》 🦕 文章图文…...

深入了解Java中SQL优化的关键技巧与实践
引言 介绍SQL优化对于Java应用性能的重要性,并概述本文将要讨论的内容。 1. 编写高效的SQL语句 - **索引的类型与使用:** 解释B-Tree索引、哈希索引等类型的区别,以及如何根据查询需求合理创建和使用索引。 - **查询优化器:** 说明…...
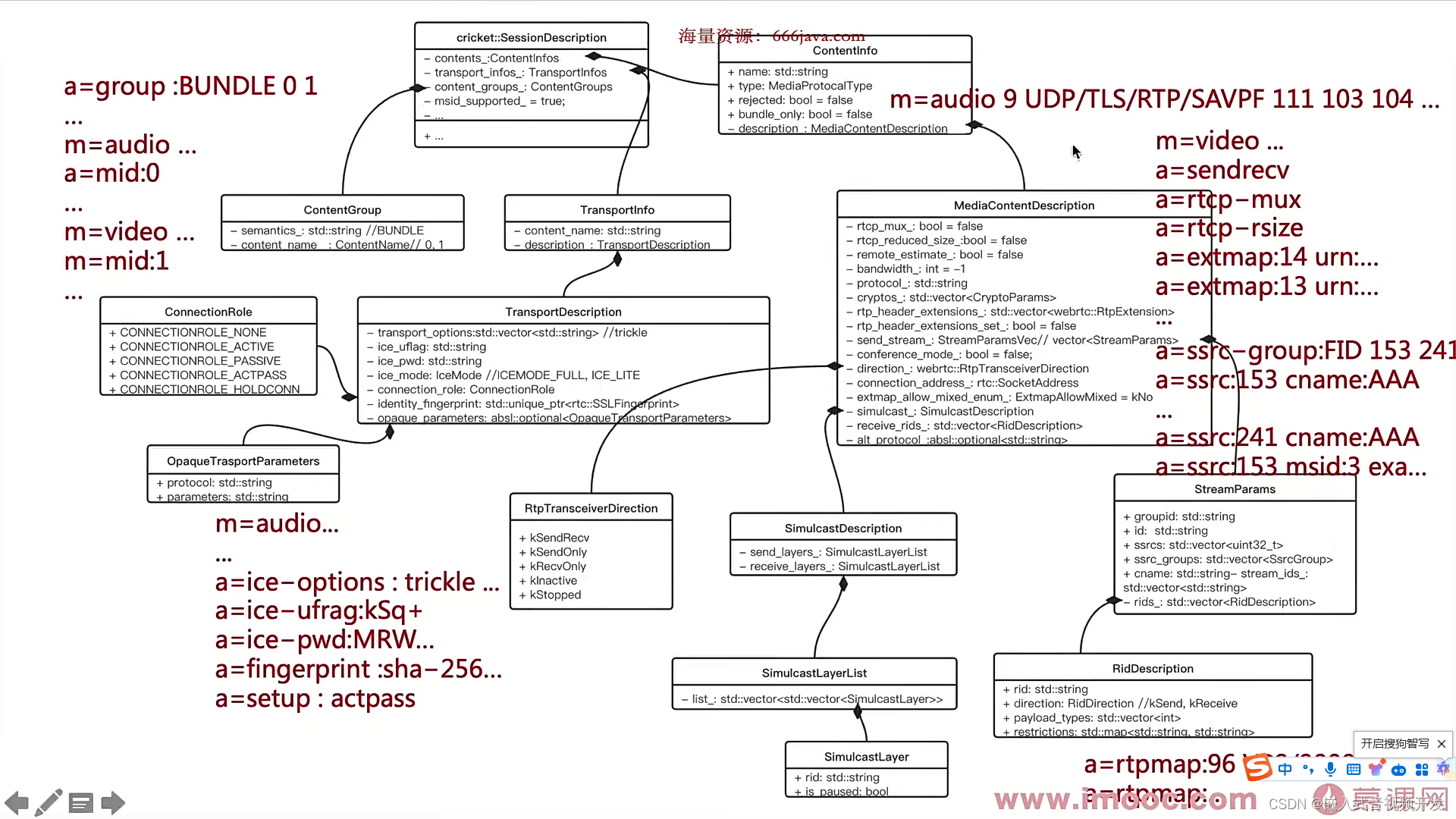
6.3.WebRTC中的SDP类的结构
在上节课中呢,我向你介绍了sdp协议, 那这节课呢,我们再来看看web rtc中。是如何存储sdp的?也就是sdp的类结构,那在此之前呢?我们先对sdp的内容啊,做一下分类。因为在上节课中呢,虽然…...
ArcGis如何用点连线?
这里指的是根据已有坐标点手动连线,类似于mapgis中的“用点连线”,线的每个拐点是可以自动捕捉到坐标点的,比直接画精确。 我也相信这么强大的软件一定可以实现类似于比我的软件上坐标时自动生成的线,但是目前我还没接触到那里&a…...

自定义精美商品分类列表组件 侧边栏商品分类组件 category组件(适配vue3)
随着技术的发展,开发的复杂度也越来越高,传统开发方式将一个系统做成了整块应用,经常出现的情况就是一个小小的改动或者一个小功能的增加可能会引起整体逻辑的修改,造成牵一发而动全身。通过组件化开发,可以有效实现单…...
)
造一个float类型二维矩阵,并将二维矩阵存快速储到一个float*中(memcpy)
// 创建并初始化一个二维数组 std::vector<std::vector<float>> createAndInitializeArray(int rows, int cols) {std::vector<std::vector<float>> array(rows, std::vector<float>(cols));float value 0.0f;for (int i 0; i < rows; i) {…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(二)
HoST框架核心实现方法详解 - 论文深度解读(第二部分) 《Learning Humanoid Standing-up Control across Diverse Postures》 系列文章: 论文深度解读 + 算法与代码分析(二) 作者机构: 上海AI Lab, 上海交通大学, 香港大学, 浙江大学, 香港中文大学 论文主题: 人形机器人…...

C++:std::is_convertible
C++标志库中提供is_convertible,可以测试一种类型是否可以转换为另一只类型: template <class From, class To> struct is_convertible; 使用举例: #include <iostream> #include <string>using namespace std;struct A { }; struct B : A { };int main…...

中南大学无人机智能体的全面评估!BEDI:用于评估无人机上具身智能体的综合性基准测试
作者:Mingning Guo, Mengwei Wu, Jiarun He, Shaoxian Li, Haifeng Li, Chao Tao单位:中南大学地球科学与信息物理学院论文标题:BEDI: A Comprehensive Benchmark for Evaluating Embodied Agents on UAVs论文链接:https://arxiv.…...

关于nvm与node.js
1 安装nvm 安装过程中手动修改 nvm的安装路径, 以及修改 通过nvm安装node后正在使用的node的存放目录【这句话可能难以理解,但接着往下看你就了然了】 2 修改nvm中settings.txt文件配置 nvm安装成功后,通常在该文件中会出现以下配置&…...

【解密LSTM、GRU如何解决传统RNN梯度消失问题】
解密LSTM与GRU:如何让RNN变得更聪明? 在深度学习的世界里,循环神经网络(RNN)以其卓越的序列数据处理能力广泛应用于自然语言处理、时间序列预测等领域。然而,传统RNN存在的一个严重问题——梯度消失&#…...

HTML 列表、表格、表单
1 列表标签 作用:布局内容排列整齐的区域 列表分类:无序列表、有序列表、定义列表。 例如: 1.1 无序列表 标签:ul 嵌套 li,ul是无序列表,li是列表条目。 注意事项: ul 标签里面只能包裹 li…...

电脑插入多块移动硬盘后经常出现卡顿和蓝屏
当电脑在插入多块移动硬盘后频繁出现卡顿和蓝屏问题时,可能涉及硬件资源冲突、驱动兼容性、供电不足或系统设置等多方面原因。以下是逐步排查和解决方案: 1. 检查电源供电问题 问题原因:多块移动硬盘同时运行可能导致USB接口供电不足&#x…...

ESP32 I2S音频总线学习笔记(四): INMP441采集音频并实时播放
简介 前面两期文章我们介绍了I2S的读取和写入,一个是通过INMP441麦克风模块采集音频,一个是通过PCM5102A模块播放音频,那如果我们将两者结合起来,将麦克风采集到的音频通过PCM5102A播放,是不是就可以做一个扩音器了呢…...

第一篇:Agent2Agent (A2A) 协议——协作式人工智能的黎明
AI 领域的快速发展正在催生一个新时代,智能代理(agents)不再是孤立的个体,而是能够像一个数字团队一样协作。然而,当前 AI 生态系统的碎片化阻碍了这一愿景的实现,导致了“AI 巴别塔问题”——不同代理之间…...

如何理解 IP 数据报中的 TTL?
目录 前言理解 前言 面试灵魂一问:说说对 IP 数据报中 TTL 的理解?我们都知道,IP 数据报由首部和数据两部分组成,首部又分为两部分:固定部分和可变部分,共占 20 字节,而即将讨论的 TTL 就位于首…...
