LeetCode 1237. Find Positive Integer Solution for a Given Equation【双指针,二分,交互】
本文属于「征服LeetCode」系列文章之一,这一系列正式开始于2021/08/12。由于LeetCode上部分题目有锁,本系列将至少持续到刷完所有无锁题之日为止;由于LeetCode还在不断地创建新题,本系列的终止日期可能是永远。在这一系列刷题文章中,我不仅会讲解多种解题思路及其优化,还会用多种编程语言实现题解,涉及到通用解法时更将归纳总结出相应的算法模板。
为了方便在PC上运行调试、分享代码文件,我还建立了相关的仓库。在这一仓库中,你不仅可以看到LeetCode原题链接、题解代码、题解文章链接、同类题目归纳、通用解法总结等,还可以看到原题出现频率和相关企业等重要信息。如果有其他优选题解,还可以一同分享给他人。
由于本系列文章的内容随时可能发生更新变动,欢迎关注和收藏征服LeetCode系列文章目录一文以作备忘。
Given a callable function f(x, y) with a hidden formula and a value z, reverse engineer the formula and return all positive integer pairs x and y where f(x,y) == z. You may return the pairs in any order.
While the exact formula is hidden, the function is monotonically increasing, i.e.:
f(x, y) < f(x + 1, y)f(x, y) < f(x, y + 1)
The function interface is defined like this:
interface CustomFunction {
public:// Returns some positive integer f(x, y) for two positive integers x and y based on a formula.int f(int x, int y);
};
We will judge your solution as follows:
- The judge has a list of
9hidden implementations ofCustomFunction, along with a way to generate an answer key of all valid pairs for a specificz. - The judge will receive two inputs: a
function_id(to determine which implementation to test your code with), and the targetz. - The judge will call your
findSolutionand compare your results with the answer key. - If your results match the answer key, your solution will be
Accepted.
题意:给你一个函数 f(x, y) 和一个目标结果 z,函数公式未知,计算方程 f(x,y) == z 所有可能的正整数 数对 x 和 y。满足条件的结果数对可以按任意顺序返回。尽管函数的具体式子未知,但它是单调递增函数,也就是说:
f(x, y) < f(x + 1, y)f(x, y) < f(x, y + 1)
解法1 双重循环
由于数据不大,可以直接暴力循环。
- 时间复杂度:O(n2)O(n^2)O(n2)
- 空间复杂度:O(1)O(1)O(1)
class Solution {
public:vector<vector<int>> findSolution(CustomFunction& customfunction, int z) {vector<vector<int>> ans;for (int x = 1; x <= 1000; ++x) {for (int y = 1; y <= 1000; ++y) {if (customfunction.f(x, y) == z) ans.push_back({x, y});}}return ans;}
};
解法2 二分
类似LeetCode 15 三数之和,循环遍历 xxx ,然后对单调递增的 yyy 进行二分搜索。
- 时间复杂度:O(nlogn)O(n\log n)O(nlogn) 。
- 空间复杂度:O(1)O(1)O(1)
class Solution {
public:vector<vector<int>> findSolution(CustomFunction& customfunction, int z) {vector<vector<int>> ans;for (int x = 1; x <= 1000; ++x) {int yl = 1, yh = 1000;while (yl <= yh) {int mid = (yl + yh) / 2, tz = customfunction.f(x, mid);if (tz == z) {ans.push_back({x, mid});break;} else if (tz > z) yh = mid - 1; // 说明y太大了else yl = mid + 1;}}return ans;}
};
解法3 抽象BST
官解告诉我们这是240题搜索二维矩阵II的变形题,如果题目读不懂,不妨看看本题前身240题搜索二维矩阵II是一道怎样的题目——这道题的题目含义就非常清晰了。最关键的信息在于,对于给定的 m×nm \times nm×n 矩阵 matrix ,存在以下性质:
- 每行的元素从左到右升序排列
- 每列的元素从上到下升序排列
用数学语言来表达的话,就是对于下标为 (x,y)(x, y)(x,y) 的元素 matrix[x][y]matrix[x][y]matrix[x][y] ,(在不越界的情况下)一定存在以下两个关系:
- matrix[x][y]<matrix[x][y+1]matrix[x][y] < matrix[x][y+1]matrix[x][y]<matrix[x][y+1] ,即同一行的元素从左往右单调递增
- matrix[x][y]<matrix[x+1][y]matrix[x][y] < matrix[x+1][y]matrix[x][y]<matrix[x+1][y] ,即同一列的元素从上往下单调递增
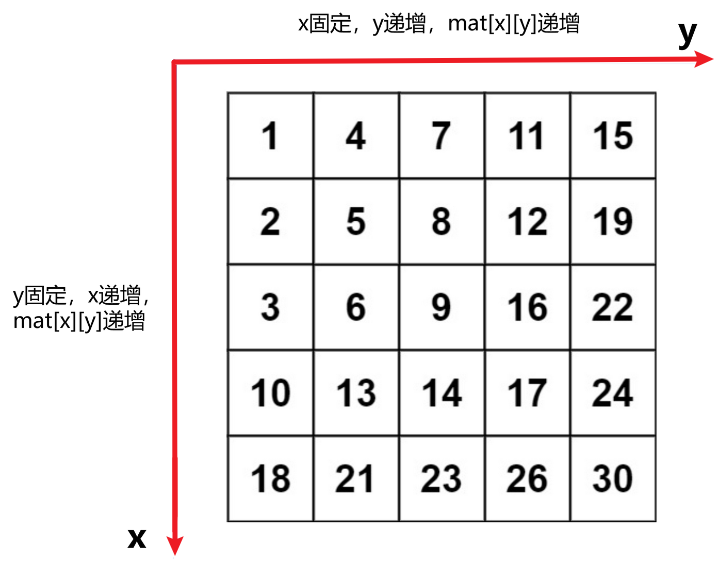
我们对240题的搜索过程如下所示:
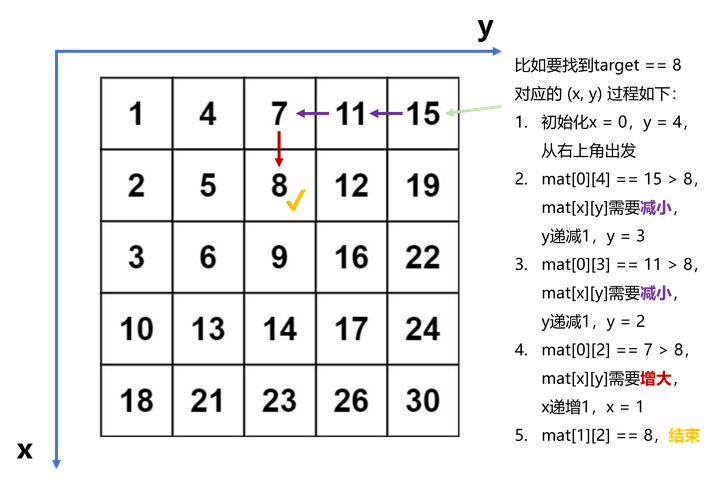
如果我们把整个矩阵matrix看作是一棵二叉树,每一个值都是一个节点,把起始点 (0,n−1)(0, n-1)(0,n−1) 看作根节点,左边的值看作是左节点,下面的值看作是右节点,那么这个二维矩阵可以抽象成一颗二叉搜索树BST。我们的搜寻过程,其实也遵循BST的搜索原则。
从而对于本题,我们也可以这么做:
- 把解也就是
x和y类似上图一样,看做一个二维矩阵,高宽均是1000(取值范围) - 从二维数组右上角开始,即 x=1,y=1000x = 1, y = 1000x=1,y=1000 为起始点,将这个起始点看为二叉搜索树的根节点
- 由于函数方程具有单调性,也就是任一点向左 (y−1)(y - 1)(y−1) 结果递减,任一点向下 (x+1)(x+1)(x+1) 结果递增
- 从起始点来看,向左对应二叉搜索树的左子结点,向下对应二叉搜索树的右子结点
- 从起始点逐个得到当前 xxx 和 yyy 的方程结果,比目标值大则向左移动,比目标值小则向下移动
- 特别处理:如果已经找到了当前方程的解之一,怎么移动都可以,往左或往下或往左下都行。
完整代码如下所示:
- 时间复杂度:O(n)O(n)O(n) 。
- 空间复杂度:O(1)O(1)O(1) 。
class Solution {
public:vector<vector<int>> findSolution(CustomFunction& customfunction, int z) {vector<vector<int>> ans;int x = 1, y = 1000; // x向右,f=(x,y)递增,y向下,f(x,y)递减while (x <= 1000 && y >= 1) {int tz = customfunction.f(x, y);if (tz == z) { // x,y合适ans.push_back({x, y});++x; // 或者--y} else if (tz < z) ++x; // tz太小,增加x以增加tzelse --y; // tz太大,减少y以减少tz}return ans;}
};
相关文章:

LeetCode 1237. Find Positive Integer Solution for a Given Equation【双指针,二分,交互】
本文属于「征服LeetCode」系列文章之一,这一系列正式开始于2021/08/12。由于LeetCode上部分题目有锁,本系列将至少持续到刷完所有无锁题之日为止;由于LeetCode还在不断地创建新题,本系列的终止日期可能是永远。在这一系列刷题文章…...

【C语言】结构体进阶
一、结构体 1. 结构体的声明 (1) 结构的基础知识 结构是一些值的集合,这些值称为成员变量。结构的每个成员可以是不同类型的变量。(2)结构的声明 struct tag {member-list; }variable-list;例如描述一个学生&#x…...
全志T3+FPGA国产核心板——Pango Design Suite的FPGA程序加载固化
本文主要基于紫光同创Pango Design Suite(PDS)开发软件,演示FPGA程序的加载、固化,以及程序编译等方法。适用的开发环境为Windows 7/10 64bit。 测试板卡为全志T3+Logos FPGA核心板,它是一款基于全志科技T3四核ARM Cortex-A7处理器 + 紫光同创Logos PGL25G/PGL50G FPGA设计…...

深度学习之 imgaug (图像增强)学习笔记
深度学习之 imgaug (图像增强)前言1\. 安装和卸载2\. 示例2.1 基本使用2.2 包含常用的变换示例3 Augmenters常用函数3.1 iaa.Sequential()3.2 iaa.someOf()3.3 iaa.OneOf()3.4 iaa.Sometimes()3.5 iaa.WithColorspace()3.6 iaa.WithChannels()3.7 iaa.No…...

mysql字符串等值查询中条件字段值末尾有空格也能查到数据问题
一、事故还原 我们仍然使用学生信息表,但是我们只需要保留两个字段即可: CREATE TABLE student_info (id int(11) NOT NULL AUTO_INCREMENT COMMENT 学号,name varchar(20) CHARACTER SET utf8 DEFAULT NULL COMMENT 姓名, PRIMARY KEY (id) ) ENGINEIn…...

一个关于事件溯源Event Sourcing的小荔枝,Golang实现
最后更新于2023年3月1日 10:23:13 参考的这个文章:https://martinfowler.com/eaaDev/EventSourcing.html 用C sharp实现的,我改写成Golang了 最简单的例子 func main() {eProc : NewEventProcessor()//refact : Cargo{Name: "Refactoring"}…...

Vue3 组合式函数,实现minxins
截至目前,组合式函数应该是在VUE 3应用程序中组织业务逻辑最佳的方法。它让我们可以把一些小块的通用逻辑进行抽离、复用,使我们的代码更易于编写、阅读和维护。 一. 什么是“组合式函数”? 根据官方文档说明,在 Vue 应用的概念中…...
什么是钉钉消息推送?
我是3y,一年CRUD经验用十年的markdown程序员👨🏻💻常年被誉为职业八股文选手 在前阵子我就已经接入了钉钉的群机器人和工作消息推送,一直没写文章同步到给大家。 像这种接入渠道的工作,虽然我没接入过&…...

利用 NVIDIATAO 和 WeightBias 加速AI开发
利用 NVIDIATAO 和 Weight&Bias 加速AI开发 利用图像分类、对象检测、自动语音识别 (ASR) 和其他形式的 AI 可以推动公司和商业部门内部的大规模转型。 然而,从头开始构建人工智能和深度学习模型是一项艰巨的任务。 构建这些模型的一个共同先决条件是拥有大量高…...

token - 令牌
文章目录token - 令牌学前须知:1,base64 防君子不防小人2,SHA-256 安全散列算法的一种(hash)3,HMAC-SHA2564,RSA256 非对称加密2.1 JWT - json-web-token1,三大组成2,jwt…...
应用模型开发指南上新介绍
Module、HAP、Ability、AbilitySta-ge、Context……您是否曾经被这些搞不懂又绕不开的知识点困扰? 现在,全新的《应用程序包基础知识》及《应用模型开发指南》为您答疑解惑! 这里有您关注的概念解析、原理机制阐述,也有丰富的…...
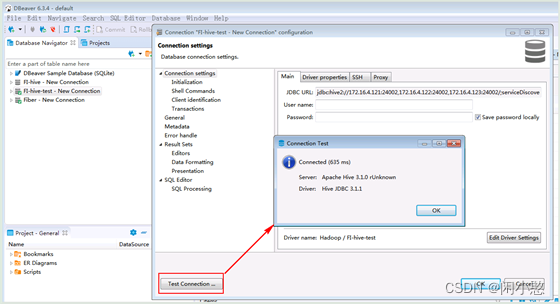
Dbeaver连接Hive数据库操作指导
背景:由于工作需要,当前分析研究的数据基于Hadoop的Hive数据库中,且Hadoop服务端无权限进行操作且使用安全模式,在研究了Dbeaver、Squirrel和Hue三种连接Hive的工具,在无法绕开useKey认证的情况下,只能使用…...
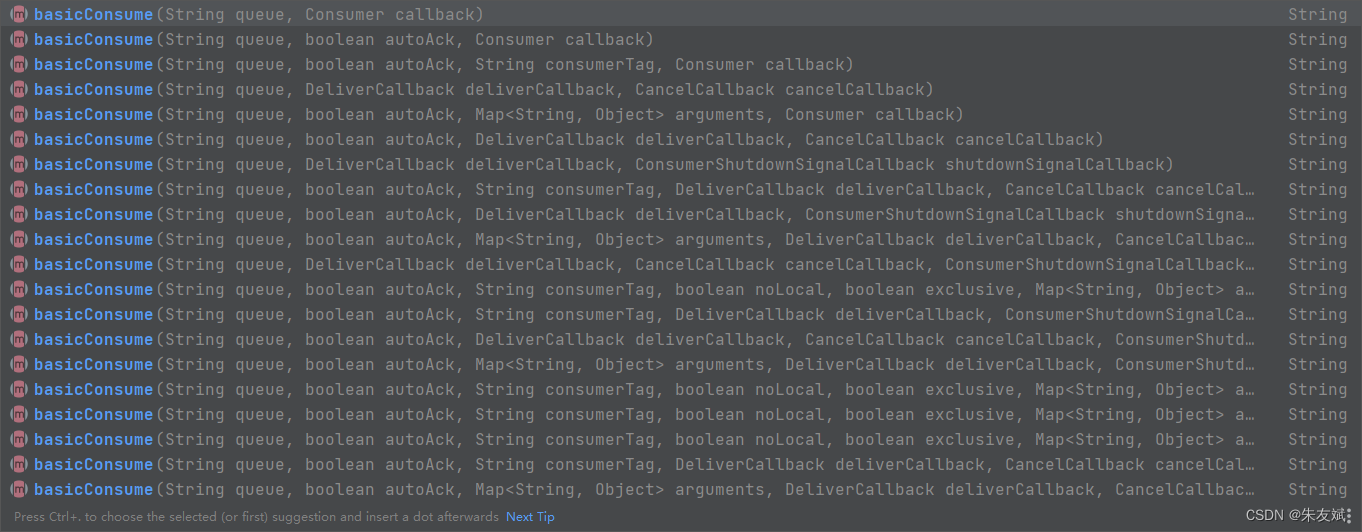
【RabbitMQ笔记09】消息队列RabbitMQ之常见方法的使用
这篇文章,主要介绍消息队列RabbitMQ之常见方法的使用。 目录 一、消息队列常见方法 1.1、连接工厂ConnectionFactory 1.2、连接Connection 1.3、通道Channel 1.4、交换机相关方法 (1)exchangeDeclare()声明交换机 1.5、队列相关方法 …...
Linux字符设备驱动模型之设备号
从上文中可知,在Linux用户空间中,如若需要操作硬件设备,均通过/dev目录下的设备文件节点进行操作,基本上每一种设备都会存在一个或者多个的设备节点。 并且在Linux内核中,其表示字符设备的结构成员也提供了相应的设备号…...

C++多态原理
请看下面的程序,该程序演示了多态类对象存储空间的大小。 #include <iostream> using namespace std; class A {public:int i;virtual void func() {}virtual void func2() {} }; class B : public A {int j;void func() {} }; int main() {cout << si…...

PMP认证与NPDP认证哪个含金量高?
两个证涉及的领域不一样的,一个是项目管理,对应的是项目经理;一个是产品管理,对应的是产品经理。含金量不能相比,但在各自的领域的含金量是很高的,至少专业程度或者知名度是最高的。 我来分别说一下PMP认证…...

改进YOLOv7-Tiny系列:首发改进结合BiFPN结构的特征融合网络,网络融合更多有效特征,高效涨点
💡该教程为改进进阶指南,属于《芒果书》📚系列,包含大量的原创首发改进方式, 所有文章都是全网首发原创改进内容🚀 内容出品:CSDN博客独家更新 @CSDN芒果汁没有芒果 💡本篇文章 基于 YOLOv5、YOLOv7芒果改进YOLO系列:芒果改进YOLOv7-Tiny系列:首发改进结合BiFPN结…...

PPC Insights系列:洞见安全多方图联邦
开放隐私计算开放隐私计算开放隐私计算OpenMPC是国内第一个且影响力最大的隐私计算开放社区。社区秉承开放共享的精神,专注于隐私计算行业的研究与布道。社区致力于隐私计算技术的传播,愿成为中国 “隐私计算最后一公里的服务区”。183篇原创内容公众号知…...
)
SQLite注入记录(目前最全、核心函数用法、布尔盲注、时间盲注、webshell、动态库,绕过方式)
目录 与Mysql区别 全部核心函数 普通注入 查询所有列 查看所有表名...
Java简单的生成/解析二维码(zxing qrcode)
Hi I’m Shendi Java简单的生成/解析二维码(zxing qrcode) 在之前使用 qrcode.js 方式生成二维码,但在不同设备上难免会有一些兼容问题,于是改为后端(Java)生成二维码图片 这里使用 Google 的 zxing包 Jar…...

多模态2025:技术路线“神仙打架”,视频生成冲上云霄
文|魏琳华 编|王一粟 一场大会,聚集了中国多模态大模型的“半壁江山”。 智源大会2025为期两天的论坛中,汇集了学界、创业公司和大厂等三方的热门选手,关于多模态的集中讨论达到了前所未有的热度。其中,…...

基于Uniapp开发HarmonyOS 5.0旅游应用技术实践
一、技术选型背景 1.跨平台优势 Uniapp采用Vue.js框架,支持"一次开发,多端部署",可同步生成HarmonyOS、iOS、Android等多平台应用。 2.鸿蒙特性融合 HarmonyOS 5.0的分布式能力与原子化服务,为旅游应用带来…...

MMaDA: Multimodal Large Diffusion Language Models
CODE : https://github.com/Gen-Verse/MMaDA Abstract 我们介绍了一种新型的多模态扩散基础模型MMaDA,它被设计用于在文本推理、多模态理解和文本到图像生成等不同领域实现卓越的性能。该方法的特点是三个关键创新:(i) MMaDA采用统一的扩散架构…...

[ICLR 2022]How Much Can CLIP Benefit Vision-and-Language Tasks?
论文网址:pdf 英文是纯手打的!论文原文的summarizing and paraphrasing。可能会出现难以避免的拼写错误和语法错误,若有发现欢迎评论指正!文章偏向于笔记,谨慎食用 目录 1. 心得 2. 论文逐段精读 2.1. Abstract 2…...

【SQL学习笔记1】增删改查+多表连接全解析(内附SQL免费在线练习工具)
可以使用Sqliteviz这个网站免费编写sql语句,它能够让用户直接在浏览器内练习SQL的语法,不需要安装任何软件。 链接如下: sqliteviz 注意: 在转写SQL语法时,关键字之间有一个特定的顺序,这个顺序会影响到…...

苍穹外卖--缓存菜品
1.问题说明 用户端小程序展示的菜品数据都是通过查询数据库获得,如果用户端访问量比较大,数据库访问压力随之增大 2.实现思路 通过Redis来缓存菜品数据,减少数据库查询操作。 缓存逻辑分析: ①每个分类下的菜品保持一份缓存数据…...

sqlserver 根据指定字符 解析拼接字符串
DECLARE LotNo NVARCHAR(50)A,B,C DECLARE xml XML ( SELECT <x> REPLACE(LotNo, ,, </x><x>) </x> ) DECLARE ErrorCode NVARCHAR(50) -- 提取 XML 中的值 SELECT value x.value(., VARCHAR(MAX))…...

【Web 进阶篇】优雅的接口设计:统一响应、全局异常处理与参数校验
系列回顾: 在上一篇中,我们成功地为应用集成了数据库,并使用 Spring Data JPA 实现了基本的 CRUD API。我们的应用现在能“记忆”数据了!但是,如果你仔细审视那些 API,会发现它们还很“粗糙”:有…...

使用Matplotlib创建炫酷的3D散点图:数据可视化的新维度
文章目录 基础实现代码代码解析进阶技巧1. 自定义点的大小和颜色2. 添加图例和样式美化3. 真实数据应用示例实用技巧与注意事项完整示例(带样式)应用场景在数据科学和可视化领域,三维图形能为我们提供更丰富的数据洞察。本文将手把手教你如何使用Python的Matplotlib库创建引…...

管理学院权限管理系统开发总结
文章目录 🎓 管理学院权限管理系统开发总结 - 现代化Web应用实践之路📝 项目概述🏗️ 技术架构设计后端技术栈前端技术栈 💡 核心功能特性1. 用户管理模块2. 权限管理系统3. 统计报表功能4. 用户体验优化 🗄️ 数据库设…...
