【数据结构】D : 图的顶点可达闭包
D : 图的顶点可达闭包
Description
给定有向图的邻接矩阵A,其元素定义为:若存在顶点i到顶点j的有向边则A[i,j]=1,若没有有向边则A[i,j]= 0。试求A的可达闭包矩阵A*,其元素定义为:若存在顶点i到顶点j的有向路径则A*[i,j]=1,若没有有向路径则A*[i,j]= 0。
Input
第1行顶点个数n
第2行开始的n行有向图的邻接矩阵,元素之间由空格分开
Output
有向图的可达闭包矩阵A*,元素之间由空格分开
Sample
Input
4
0 1 0 1
0 0 1 0
0 0 0 0
0 0 0 0
Output
0 1 1 1
0 0 1 0
0 0 0 0
0 0 0 0
解题思路
一开始我不知道闭包是啥东西,查了一下,通俗点讲就是:如果在图中存在一个从顶点i到顶点j的有向路径(不论这个路径有多长),则在A中,元素A[i, j] = 1。知道了这个之后就会想到Floyd算法,这个算法是**考虑所有可能的中间顶点,并逐步更新每一对顶点之间的最短路径。**放在这道题就是从顶点i到顶点j之间的所有可能的顶点,全部逐步拼接起来。先来看看Floyd算法:
int data[maxn][maxn];
void Floyd(int n)
{for (int k = 0; k < n; k++)for (int i = 0; i < n; i++)for (int j = 0; j < n; j++)data[i][j]=min(data[i][j], data[i][k]+data[k][j]);
}
三重循环的工作原理
-
外层循环(遍历中间顶点k):
- 这个循环遍历图中的每一个顶点,将其作为潜在的“中间顶点”。这里的“中间顶点”是指可能位于一条从顶点i到顶点j路径上的任何顶点。每一次循环都会考虑通过这个中间顶点k的所有可能路径。
-
中间层循环(遍历起始顶点i):
- 对于每一个顶点k,这个循环遍历图中的每一个顶点i,将其作为路径的起始点。这个循环的目的是考虑从顶点i出发,经过顶点k,到达任意顶点j的所有可能路径。
-
内层循环(遍历结束顶点j):
- 对于每一对顶点i和k,这个循环遍历图中的每一个顶点j,将其作为路径的结束点。这个循环的目的是完成路径的考虑,检查是否通过顶点k可以找到从i到j的更短路径。
如何更新距离矩阵
在这三个循环中,距离矩阵dist[i][j]表示从顶点i到顶点j的当前已知最短路径长度。在每次迭代中,算法馋死通过中间顶点k来改进这个距离。具体的,算法检查是否dist[i][k] + dist[k][j](即通过k的路径长度)小于当前的dist[i][j]。如果是,那么就更新dist[i][j]为这个较小的值。
这意味着算法在每次迭代中都在考虑加入一个新的中间顶点,看是否可以通过这个新的中间顶点找到更短的路径。通过逐步考虑所有可能的中间顶点,算法能够确保找到所有顶点对之间的最短路径。
为什么k放在第一个循环
将k放在最外层循环是逐步构建最短路径的关键。这种方法允许算法首先考虑所有通过单个中间顶点的路径,然后是通过两个中间顶点的路径,以此类推,直到考虑了通过所有中间顶点的路径。这样做确保了算法能够逐步建立起从每个起始点到每个目的地的最短路径,考虑了所有可能的中间步骤。
换句话说,k在第一个循环中意味着你首先考虑所有可能的捷径(中间城市),然后基于这些捷径找出所有的最短路线。确保没有遗漏任何可能的捷径,从而可以找到从任何一个城市到达另一个城市的真正最短路线。
说了这么多其实这就是floyd算法的思想,知道了这个思想就可以直接求解这一道题,但是这一道题不需要求解最短路径,只要说明有路可走,同时动态规划的方程不适用了。上代码看吧:
AC代码:
#include <iostream>
using namespace std;
const int MAX_N = 50;
void floyd(int graph[][MAX_N], int n) {int dist[MAX_N][MAX_N];// 初始化距离矩阵for (int i = 0; i < n; i++) {for (int j = 0; j < n; j++) {dist[i][j] = graph[i][j];}}// 弗洛伊德算法for (int k = 0; k < n; k++) {for (int i = 0; i < n; i++) {for (int j = 0; j < n; j++) {// 如果i到k和k到j之间有路径,则设置i到j有路径if (dist[i][k] == 1 && dist[k][j] == 1) {dist[i][j] = 1;}}}}// 打印可达闭包矩阵for (int i = 0; i < n; i++) {for (int j = 0; j < n; j++) {cout << dist[i][j] << " ";}cout << endl;}
}int main() {int n;cin >> n;int graph[MAX_N][MAX_N];// 邻接矩阵for (int i = 0; i < n; i++) {for (int j = 0; j < n; j++) {cin >> graph[i][j];}}// 计算并打印可达闭包矩阵floyd(graph, n);return 0;
}相关文章:

【数据结构】D : 图的顶点可达闭包
D : 图的顶点可达闭包 Description 给定有向图的邻接矩阵A,其元素定义为:若存在顶点i到顶点j的有向边则A[i,j]1,若没有有向边则A[i,j] 0。试求A的可达闭包矩阵A*,其元素定义为:若存在顶点i到顶点j的有向路径则A*[i,j…...
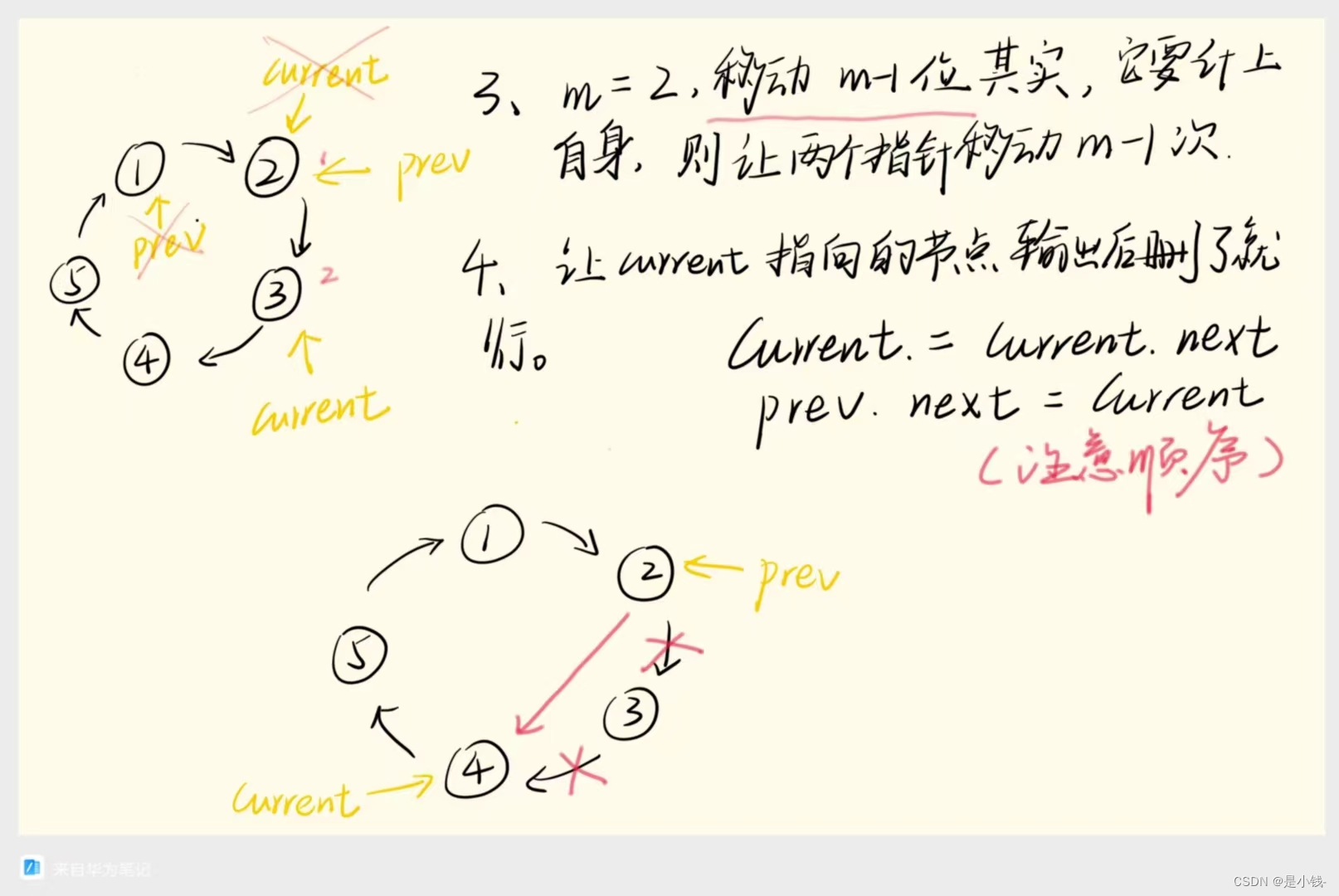
链表?细!详细知识点总结!
链表 定义:链表是一种递归的数据结构,它或者为空(null),或者是指向一个结点(node)的引用,该结点含有一个泛型的元素和一个指向另一条链表的引用。 其实链表就是有序的列表,它在内…...
【数据结构实验】排序(三)快速排序算法的改进(三者取中法)
文章目录 1. 引言2. 快速排序算法2.1 传统快速排序2.2 三者取中法 3. 实验内容3.1 实验题目(一)输入要求(二)输出要求 3.2 算法实现 4. 实验结果 1. 引言 快速排序是一种经典的排序算法,其核心思想是通过选择一个基准元…...
【数据结构/C++】栈和队列_顺序栈
#include<iostream> using namespace std; #define MaxSize 10 // 1. 顺序栈 typedef int ElemType; struct Stack {ElemType data[MaxSize];int top; } SqStack; // 初始化栈 void init(Stack &s) {// 初始化栈顶指针s.top -1; } // 入栈 bool push(Stack &s, …...
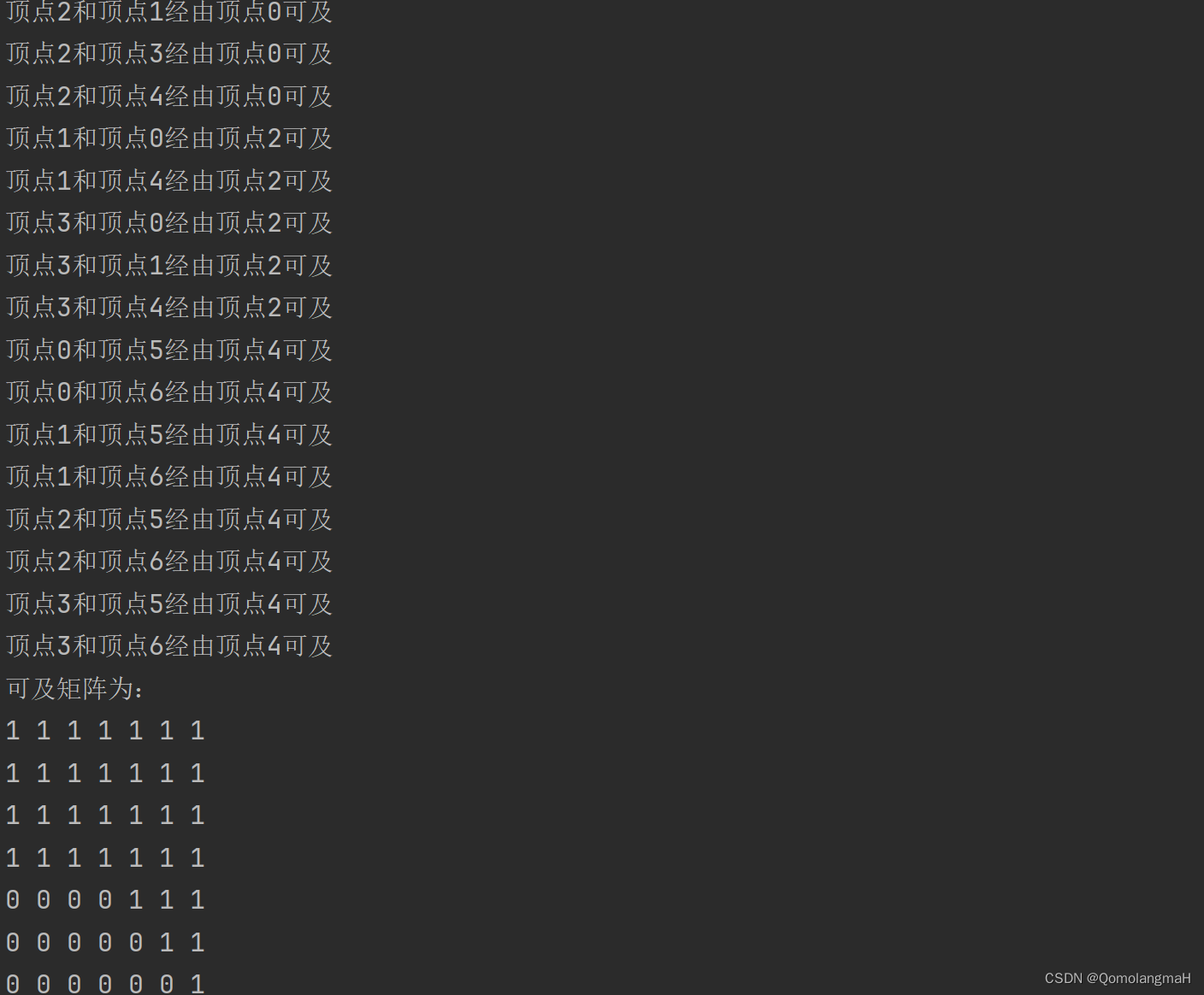
【数据结构实验】图(一)Warshall算法(求解有向图的可达矩阵)
文章目录 1. 引言2. Warshall算法原理2.0 图的基础知识a. 类型b. 表示 2.1 初始化可及矩阵2.2 迭代更新可及矩阵 3. 实验内容3.1 实验题目(一)输入要求(二)输出要求 3.2 算法实现 4. 实验结果 1. 引言 Warshall算法是一种用于求解…...
java协同过滤算法 springboot+vue游戏推荐系统
随着人们生活质量的不断提高以及个人电脑和网络的普及,人们的业余生活质量要求也在不断提高,选择一款好玩,精美,画面和音质,品质优良的休闲游戏已经成为一种流行的休闲方式。可以说在人们的日常生活中,除了…...

Android设计模式--适配器模式
至诚之道,可以前知 一,定义 适配器模式把一个类的接口变换成客户端所期待的另一种接口,从而使原本因接口不匹配而无法在一起工作的两个类能够在一起工作。 适配器模式在我们的开发中使用率极高,ListView,GridView&am…...

jQuery_06 基本过滤器的使用
什么是过滤器? 过滤器就是用来筛选dom对象的,过滤器是和选择器一起使用的。在选择了dom对象后在进行过滤筛选。 jQuery对象中存储的dom对象顺序与页面标签声明有关系。 声明顺序就是dom中存放的顺序 1.基本过滤器 使用dom对象在数组中的位置来作为过滤条…...
Kotlin学习——kt里面的函数,高阶函数 函数式编程 扩展函数和属性
Kotlin 是一门现代但已成熟的编程语言,旨在让开发人员更幸福快乐。 它简洁、安全、可与 Java 及其他语言互操作,并提供了多种方式在多个平台间复用代码,以实现高效编程。 https://play.kotlinlang.org/byExample/01_introduction/02_Functio…...
AI绘画“湿地公园的美女”
1、AI绘画:湿地公园的美女 通过输入描述:你需要什么场景的什么创作内容,AI根据内容创造出适合的主题 如图所示:请帮我创作一个湿地公园的像高圆圆的美女图片。 输出的结果如下:总体来说感觉还是非常快,基…...
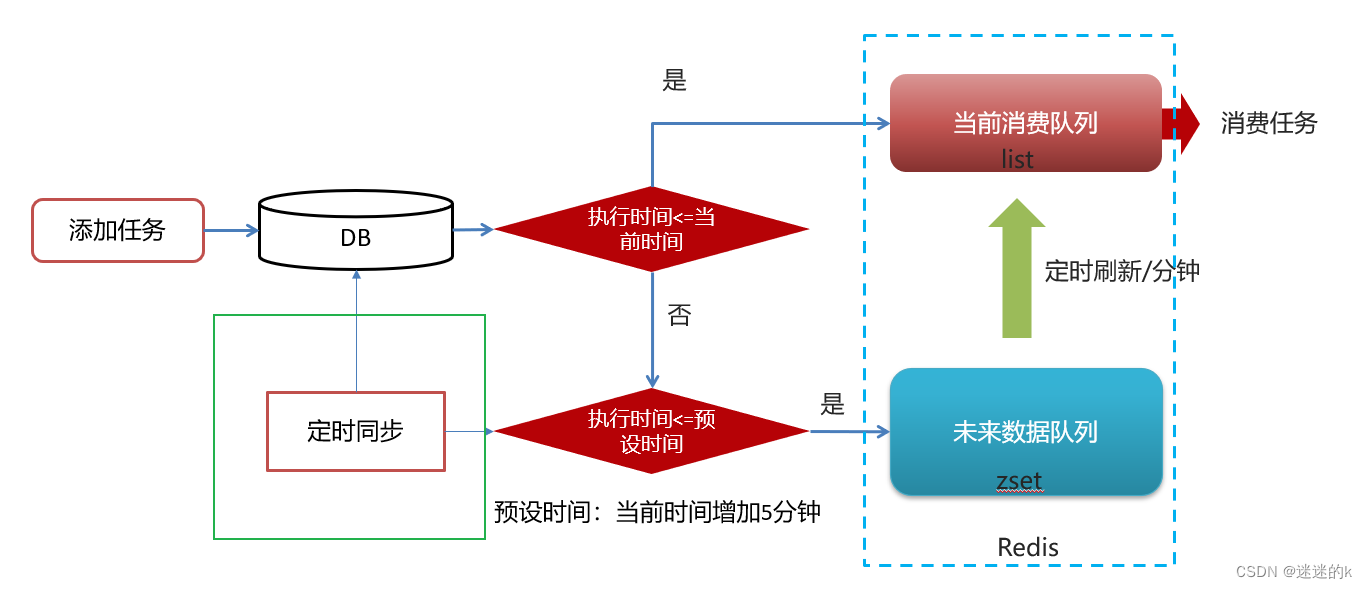
延时任务定时发布,基于 Redis 与 DB 实现
目录 1、什么是延时任务,分别可以使用哪些技术实现? 1.2 使用 Redis 和 DB 相结合的思路图以及分析 2、实现添加任务、取消任务、拉取任务 3、实现未来数据的定时更新 4、将数据库中的任务数据,同步到 Redis 中 1、什么是延时任务ÿ…...

Nacos安装使用
Nacos安装使用 官方下载地址: https://github.com/alibaba/nacos/releases 官方文档地址: https://nacos.io/zh-cn/docs/quick-start.html Nacos介绍 Nacos是阿里巴巴开源的一款支持服务注册与发现,配置管理以及微服务管理的组件。用来取代以前常用的注册中心&a…...
了解抽象思维的应用与实践
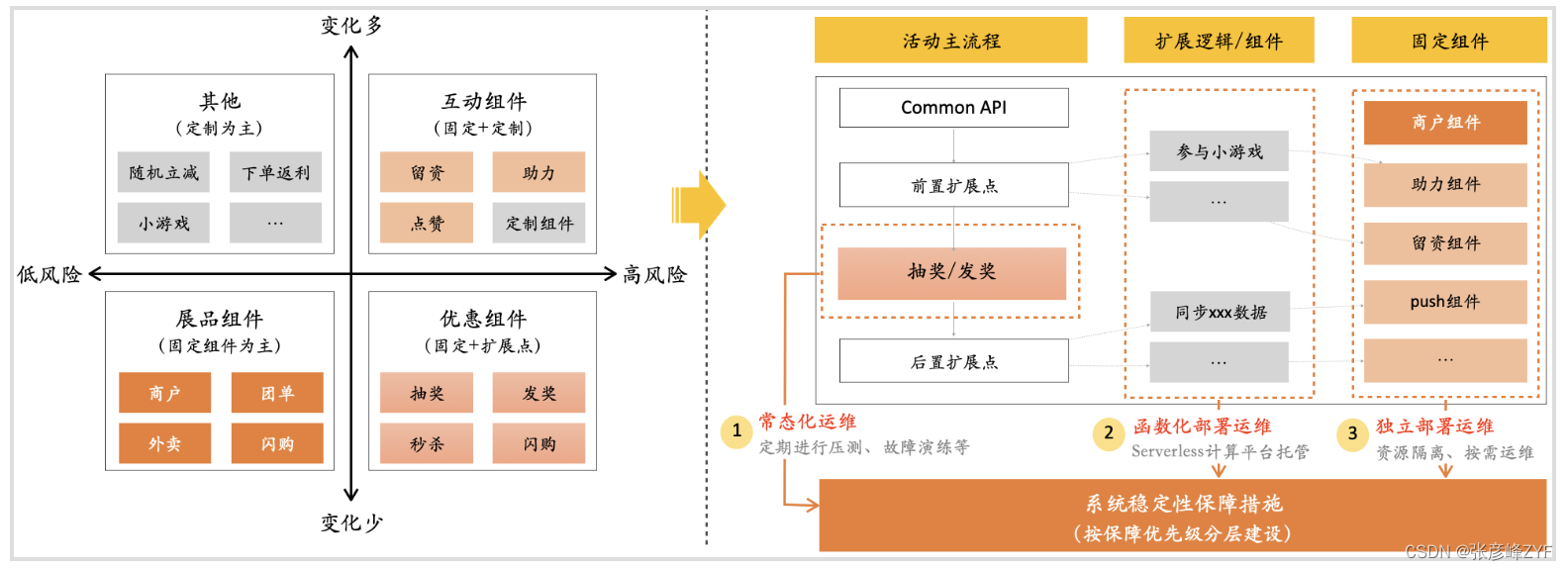
目录 一、快速了解抽象思维 (一)抽象思维的本质理解 (二)系统架构中的重要性 (三)软件开发中抽象的基本过程思考 意识和手段 抽象的方式 抽象层次的权衡 二、业务中的应用实践 (一&…...
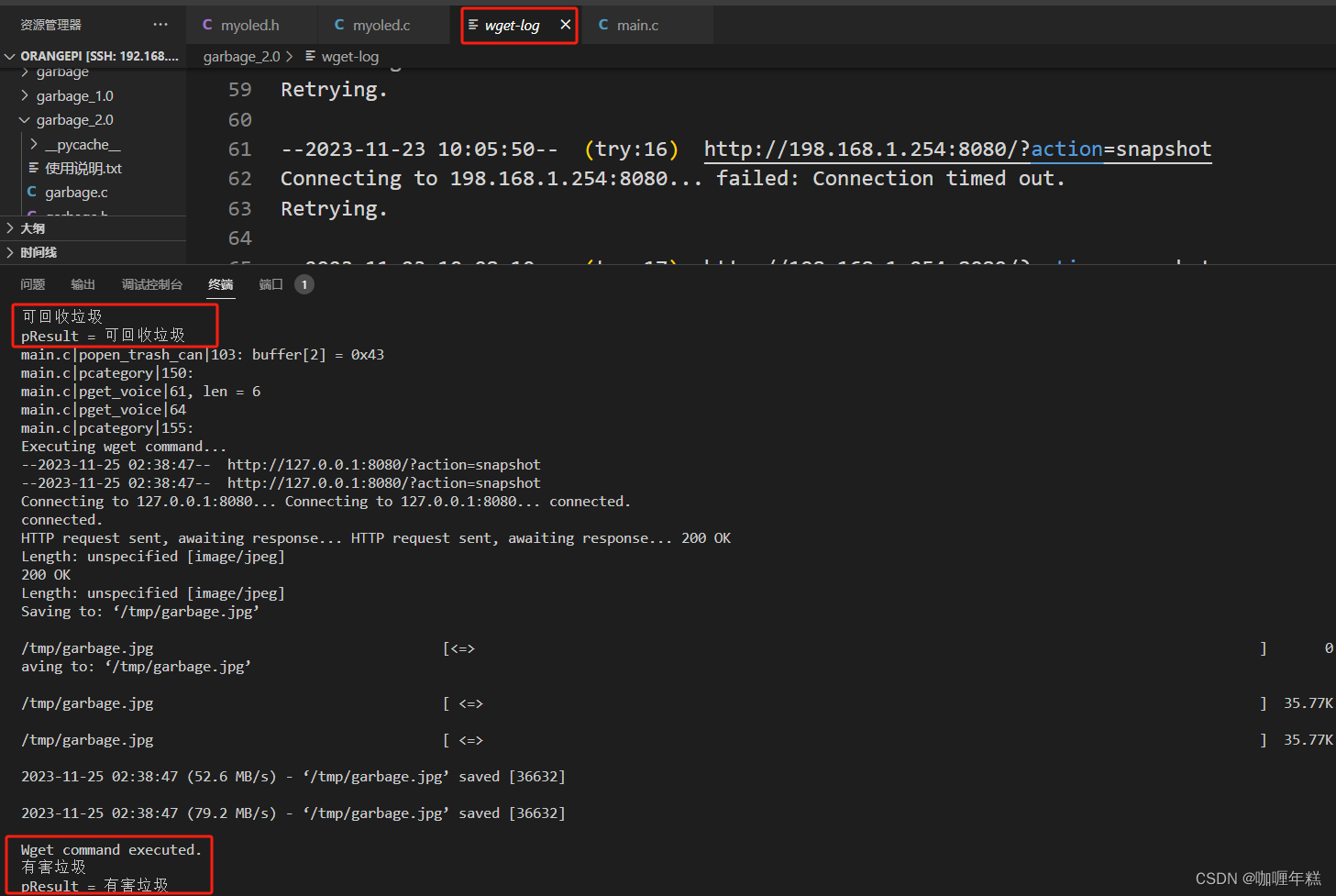
【阿里云】图像识别 智能分类识别 增加垃圾桶开关盖功能点和OLED显示功能点(二)
一、增加垃圾桶开关盖功能 环境准备 二、PWM 频率的公式 三、pthread_detach分离线程,使其在退出时能够自动释放资源 四、具体代码实现 图像识别数据及调试信息wget-log打印日志文件 五、增加OLED显示功能 六、功能点实现语音交互视频 一、增加垃圾桶开关盖功能…...
linux centos上安装python3.11.x详细完整教程
一. 安装步骤 注意: 1、安装python3.11的其他版本替换下面的版本信息即可。(如想安装3.11.5将案例中的3.11.0替换成3.11.5即可) #下载最新的软件安装包 wget https://www.python.org/ftp/python/3.11.0/Python-3.11.0.tgz#解压缩安装包 tar -xzf Python-3.11.0.tg…...
itext - PDF模板套打
目录 环境配置 快速使用 代码实现 添加图片 封装 项目需求:获取列表数据之后直接将数据生成一个pdf。因此需要使用到 itext 对pdf进行直接操作。 环境配置 需要为pdf添加文字域,因此需要安装Adobe Acrobat 准备一个空的PDF文件,如果有现…...

指针的使用和传址调用
1.引入 学习指针的⽬的是使⽤指针解决问题,那什么问题,⾮指针不可呢? 例如:写⼀个函数,交换两个整型变量的值。 ⼀番思考后,我们可能写出这样的代码: #include <stdio.h> void Swap1(int…...

【Leetcode】【实现循环队列】【数据结构】
代码实现: typedef struct {int front;int back;int k;int* a;} MyCircularQueue;bool myCircularQueueIsEmpty(MyCircularQueue* obj) {return obj->frontobj->back; }bool myCircularQueueIsFull(MyCircularQueue* obj) {return (obj->back1)%(obj->…...
)
电力感知边缘计算网关产品设计方案-软件架构(业务流程)
软件架构(业务流程) 基于前端系统提供的硬件通信平台,后端系统以控制执行单元为核心,协同控制通信管理、驱动适配、存储单元等职能单元完成与前端系统的通信数据交互业务,在经历以下业务流程后,完成设备自适应通信业务功能。 1.外部设备通信前端系统 前端系统连接新的…...

【labelimg打不开】
labelimg打不开 一、 报错1.1 排除错误 **解决方法:** 一、 报错 当运行labelimg程序报错此条时 AssertionError: Missing string id : useDefaultLabel 1.1 排除错误 第一,进入创建的虚拟环境,输入pip list 查看是否安装了labelimg 第二&…...
)
浏览器访问 AWS ECS 上部署的 Docker 容器(监听 80 端口)
✅ 一、ECS 服务配置 Dockerfile 确保监听 80 端口 EXPOSE 80 CMD ["nginx", "-g", "daemon off;"]或 EXPOSE 80 CMD ["python3", "-m", "http.server", "80"]任务定义(Task Definition&…...

RocketMQ延迟消息机制
两种延迟消息 RocketMQ中提供了两种延迟消息机制 指定固定的延迟级别 通过在Message中设定一个MessageDelayLevel参数,对应18个预设的延迟级别指定时间点的延迟级别 通过在Message中设定一个DeliverTimeMS指定一个Long类型表示的具体时间点。到了时间点后…...

PHP和Node.js哪个更爽?
先说结论,rust完胜。 php:laravel,swoole,webman,最开始在苏宁的时候写了几年php,当时觉得php真的是世界上最好的语言,因为当初活在舒适圈里,不愿意跳出来,就好比当初活在…...

阿里云ACP云计算备考笔记 (5)——弹性伸缩
目录 第一章 概述 第二章 弹性伸缩简介 1、弹性伸缩 2、垂直伸缩 3、优势 4、应用场景 ① 无规律的业务量波动 ② 有规律的业务量波动 ③ 无明显业务量波动 ④ 混合型业务 ⑤ 消息通知 ⑥ 生命周期挂钩 ⑦ 自定义方式 ⑧ 滚的升级 5、使用限制 第三章 主要定义 …...

基于ASP.NET+ SQL Server实现(Web)医院信息管理系统
医院信息管理系统 1. 课程设计内容 在 visual studio 2017 平台上,开发一个“医院信息管理系统”Web 程序。 2. 课程设计目的 综合运用 c#.net 知识,在 vs 2017 平台上,进行 ASP.NET 应用程序和简易网站的开发;初步熟悉开发一…...

练习(含atoi的模拟实现,自定义类型等练习)
一、结构体大小的计算及位段 (结构体大小计算及位段 详解请看:自定义类型:结构体进阶-CSDN博客) 1.在32位系统环境,编译选项为4字节对齐,那么sizeof(A)和sizeof(B)是多少? #pragma pack(4)st…...

linux arm系统烧录
1、打开瑞芯微程序 2、按住linux arm 的 recover按键 插入电源 3、当瑞芯微检测到有设备 4、松开recover按键 5、选择升级固件 6、点击固件选择本地刷机的linux arm 镜像 7、点击升级 (忘了有没有这步了 估计有) 刷机程序 和 镜像 就不提供了。要刷的时…...

1.3 VSCode安装与环境配置
进入网址Visual Studio Code - Code Editing. Redefined下载.deb文件,然后打开终端,进入下载文件夹,键入命令 sudo dpkg -i code_1.100.3-1748872405_amd64.deb 在终端键入命令code即启动vscode 需要安装插件列表 1.Chinese简化 2.ros …...

使用van-uploader 的UI组件,结合vue2如何实现图片上传组件的封装
以下是基于 vant-ui(适配 Vue2 版本 )实现截图中照片上传预览、删除功能,并封装成可复用组件的完整代码,包含样式和逻辑实现,可直接在 Vue2 项目中使用: 1. 封装的图片上传组件 ImageUploader.vue <te…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院查看报告小程序
一、开发环境准备 工具安装: 下载安装DevEco Studio 4.0(支持HarmonyOS 5)配置HarmonyOS SDK 5.0确保Node.js版本≥14 项目初始化: ohpm init harmony/hospital-report-app 二、核心功能模块实现 1. 报告列表…...
