C++ 动态规划 DP教程 (一)思考过程(*/ω\*)
动态规划是一种思维方法,大家首先要做的就是接受这种思维方法,认同他,然后再去运用它解决新问题。
动态规划是用递推的思路去解决问题。
首先确定问题做一件什么事情?
对这件事情分步完成,分成很多步。
如果我们把整件事称为原问题,那么原问题去掉最后一步后,剩下的问题就称为子问题。
子问题和原问题是同性质的问题,子问题被原问题包含,原问题是在子问题的基础上推进一步得到的,所以用递推去求解。
子问题推进一步,得到原问题。哪些量在变化。这些变化的量用变量表示出来就是问题的状态。
子问题推进一步,这一步做了什么,就是决策。每一步的决策连续起来,就是做整件事的一个方案。
我们来看一道例题吧!ヾ(o・ω・)ノ
例1:组合问题,从n个不同物体中选择m个,求有多少种选择方案。
思考过程:
1、 题目要我们做一件什么事情?
答:选物体,确切的说是要我们从n个物体中选出m个物体。n和m尽管不知道是多少,但是肯定是一个确定的值,由输入数据确定,所以我们可以假设n=10,m=5,问题是要我们从10个物体中选出5个物体
2、 这件事分多少步去完成?
答:分10步完成,第一步考虑第一个物体选还是不选,第二步考虑第二个物体选还是不选,……,第10步考虑第10个物体选还是不选?
3、 原问题是什么?子问题是什么?
答:
整个问题是:从10个不同物体中选择5个。最后一步是确定第10个物体选还是不选。
如果第10个物体选了,那么去掉这一步,前9步还需要选择4个物体,所以剩下的子问题是从9个物体中选取4个。
如果第10个物体没有选,那么去掉这一步,在前9步还需要选择5个物体,所以剩下的子问题是从9个物体中选取5个。
原问题是10个中选5个,子问题是9个中选4个、9个中选5个
4、 子问题和原问题是同一个性质的问题,用数学符号描述这个问题,需要几个变量才能体系原问题和子问题的差异,各自表示什么含义?
答:原问题和子问题中,备选物体的规模在变化,选出来的物体数目在变化,所以用两个变量来表示问题变化的量:a表示备选物体的数目,b表示选出的物体数目,f(a,b)整个符号的含义就是从a个不同物体中选取b个物体的方案数,这里的f就是表示求解目标,方案数。
很显然,当a取值10,b取值5时,f(10,5)表示原问题,f(9,5)、f(9,4)表示子问题。用问题和子问题都是用同一个模式来表示,这就是状态。
5、 有了状态,我们就可以寻找子问题和原问题之间的递推关系了。
答:
原问题去掉最后一步,得到的子问题,寻找二者之间的关系。
f(a,b)表示从a个不同物体中选取b个,得到的方案数。
对最后一步分两种情况讨论:
选取第a个物体,则方案数等价于从剩下的a-1个物体中选取b-1个,即f(a-1,b-1)
不选第a个物体,则方案数等价于从剩下的a-1个物体中选取b个,即f(a-1,b)
所以得到一个递推方程:f[a,b]=f[a-1,b-1]+f[a-1,b]
6、 状态在计算机中用数组表示,数组第一维下标表示第一个变量,第二维下标表示第二个变量。则一个状态对应一个数组元素,状态之间递推等价于给数组元素递推赋值。
好了看前面的文章,你应该知道了如何思考动态规划的题目!
但是一道题是不够的,要做很多道题,你才能彻底的理解动态规
划的解题思路,从而得到方程,写出代码!ヽ(・ω・´メ)
话不多说,我们再来看一道题目吧!
【洛谷】P1255 数数梯
原题地址:https://www.luogu.org/problem/P1255
思路:
这个题目隐藏深一些。
题目要我们求等式的个数,我们可以穷举等号右边的和数,如果我们把数列从小到大排列,这样等号左边的数就全部位于穷举的数的左边(想不明白为什么需要排序,暂时可以放一放,假设数列就是已经排好序的)。
对于每个穷举的合数,我们目标是寻找在他左边有多少个合法的式子的和等于他。
思考过程:
1、 题目要我们做一件什么事情?
答:求所有的数学式子,确切的说,当我们穷举第i个和数时,是要我们从i-1个数中选出若干个数,使得这些数的和是a[i]。i是穷举的,是定值。
2、这件事分多少步去完成?
答:分i-1步完成,第一步考虑第一个数选还是不选,第二步考虑第二个数选还是不选,……,第i-1步考虑第i-1个数选还是不选?
3、原问题是什么?子问题是什么?
答:
整个问题是:从i-1个数中选择若干个,使得总和是a[i]。最后一步是确定第i-1个数选还是不选。
如果第i-1个数选了,那么去掉这一步,前i-2步还需要选择若干个数,使得和为a[i]-a[i-1],所以剩下的子问题是从i-2个数中选若干个,使得总和是a[i]-a[i-1]。
如果第i-1个物体没有选,那么去掉这一步,在前i-2步还需要选择若干个数使得总和为a[i],所以剩下的子问题是从i-2个数中选若干个,使得总和是a[i]。
原问题是从i-1个数中选择若干个,使得总和是a[i]。子问题是从i-2个数中选若干个,使得总和是a[i]-a[i-1];i-2个数中选若干个,使得总和是a[i]。
4、子问题和原问题是同一个性质的问题,用数学符号描述这个问题,需要几个变量才能体系原问题和子问题的差异,各自表示什么含义?
答:原问题和子问题中,备选数的规模在变化,选出来的和在变化,所以用两个变量来表示问题变化的量:x表示备选物体的数目,y表示选出的物体数目,f(x,y)整个符号的含义就是从x个数中选若干个使得总和为y的方案数,这里的f就是表示求解目标,方案数。
很显然,当x取值i-1,y取值a[i]时,f(i-1,a[i])表示原问题,f(i-2,a[i]-a[i-1])、f(i-2,a[i])表示子问题。用问题和子问题都是用同一个模式来表示,这就是状态。
5、有了状态,我们就可以寻找子问题和原问题之间的递推关系了。
答:
原问题去掉最后一步,得到的子问题,寻找二者之间的关系。
f(x,y)表示从x个数中选若干个使得和为y,得到的方案数。
对最后一步分两种情况讨论:
选取第x个数,则方案数等价于从剩下的x-1个数中选若干个使得和为y-a[x],即f(x-1,y-a[x])
不选第x个数,则方案数等价于从剩下的x-1个数中选若干个使得和为y,即f(x-1,y)
所以得到一个递推方程:f[x,y]=f[x-1,y-a[x]]+f[x-1,y]
使用该递推方程,可以求每一个阶段的状态
6、状态在计算机中用数组表示,数组第一维下标表示第一个变量,第二维下标表示第二个变量。则一个状态对应一个数组元素,状态之间递推等价于给数组元素递推赋值。
好了,本篇文章就结束了,如果喜欢就记得三连哦φ(>ω<*) ,记得多多做题哦,bye!ヾ(o・ω・)ノ
相关文章:
C++ 动态规划 DP教程 (一)思考过程(*/ω\*)
动态规划是一种思维方法,大家首先要做的就是接受这种思维方法,认同他,然后再去运用它解决新问题。 动态规划是用递推的思路去解决问题。 首先确定问题做一件什么事情? 对这件事情分步完成,分成很多步。 如果我们把整件…...
】文件和异常详解:使用、读取、写入、追加、保存用户的信息,以及优雅的处理异常)
【python基础(九)】文件和异常详解:使用、读取、写入、追加、保存用户的信息,以及优雅的处理异常
文章目录 一. 从文件中读取数据1. 读取整个文件2. 文件路径3. 逐行读取4. 创建一个包含文件各行内容的列表 二. 写入文件1. 写入空文件2. 写入多行3. 附加到文件 三. 异常1. 处理ZeroDivisionError异常2. 使用try-except代码块3. try-except-else ing4. 处理FileNotFoundError异…...

详解C语言中的指针数组和数组指针
指针数组和数组指针是 C 语言中比较常见的两种类型。它们虽然名字很相似,但是含义、用法以及指向类型都不同,需要分开理解。 指针数组 指针数组是一个数组,其中每个元素都是一个指针。这些指针可以指向不同类型的数据,也可以指向…...

【done】剑指offer18:删除链表指定节点
力扣,https://leetcode.cn/problems/shan-chu-lian-biao-de-jie-dian-lcof/description/ // 自己写的答案 class Solution {public ListNode deleteNode(ListNode head, int val) {if (head null) {return null;}if (head.val val) {return head.next;}ListNode …...

图形编辑器开发:缩放和旋转控制点
大家好,我是前端西瓜哥。好久没写图形编辑器开发的文章了。 今天来讲讲控制点。它是图形编辑器的不可缺少的基础功能。 控制点是吸附在图形上的一些小矩形和圆形点击区域,在控制点上拖拽鼠标,能够实时对被选中进行属性的更新。 比如使用旋…...
【2023 云栖】阿里云田奇铣:大模型驱动 DataWorks 数据开发治理平台智能化升级
云布道师 本文根据 2023 云栖大会演讲实录整理而成,演讲信息如下: 演讲人:田奇铣 | 阿里云 DataWorks 产品负责人 演讲主题:大模型驱动 DataWorks 数据开发治理平台智能化升级 随着大模型掀起 AI 技术革新浪潮,大数…...
Rust语言入门教程(二) - 变量与作用域
变量与作用域 变量的声明与初始化 Rust的基本语法格式如下: fn main(){let bunnies 2; }语句以分号结尾,用花括号包含语句块。 Rust的语法其实借鉴了很多其他的语言,比如C语言和Python, 所以变量定义的格式看起来也跟很多我们…...

芯知识 | Flash可更换声音语音芯片—引领音频IC技术革新的新篇章
随着科技的飞速发展,人们对于电子产品的音频性能要求越来越高。在这种背景下,Flash可更换声音语音芯片应运而生,成为音频技术领域的一颗璀璨明星。本文将详细介绍Flash可更换声音语音芯片的特点、优势以及应用场景,展望其在未来科…...

合共软件创新亮相:第102届上海电子展成就技术新篇章
2023年,第102届中国(上海)电子展活动在全球瞩目中圆满落幕。作为下半年华东地区最具影响力的电子展会,此次盛会吸引了来自全球的600家领先企业,共同探讨电子元器件行业的最新发展成果和趋势。 本届展会围绕核心先导元器…...

Ubuntu20.04清理垃圾vscode缓存
使用VM虚拟机安装了Ubuntu系统,主目录空间越来越小,硬盘扩容之后很快又空间不足,甚至出现了开机卡黑屏的情况,这里记录一下解决过程。 1 重新开机进入系统 状态:卡到了开机黑屏状态,左上角有一条小横杠 原…...
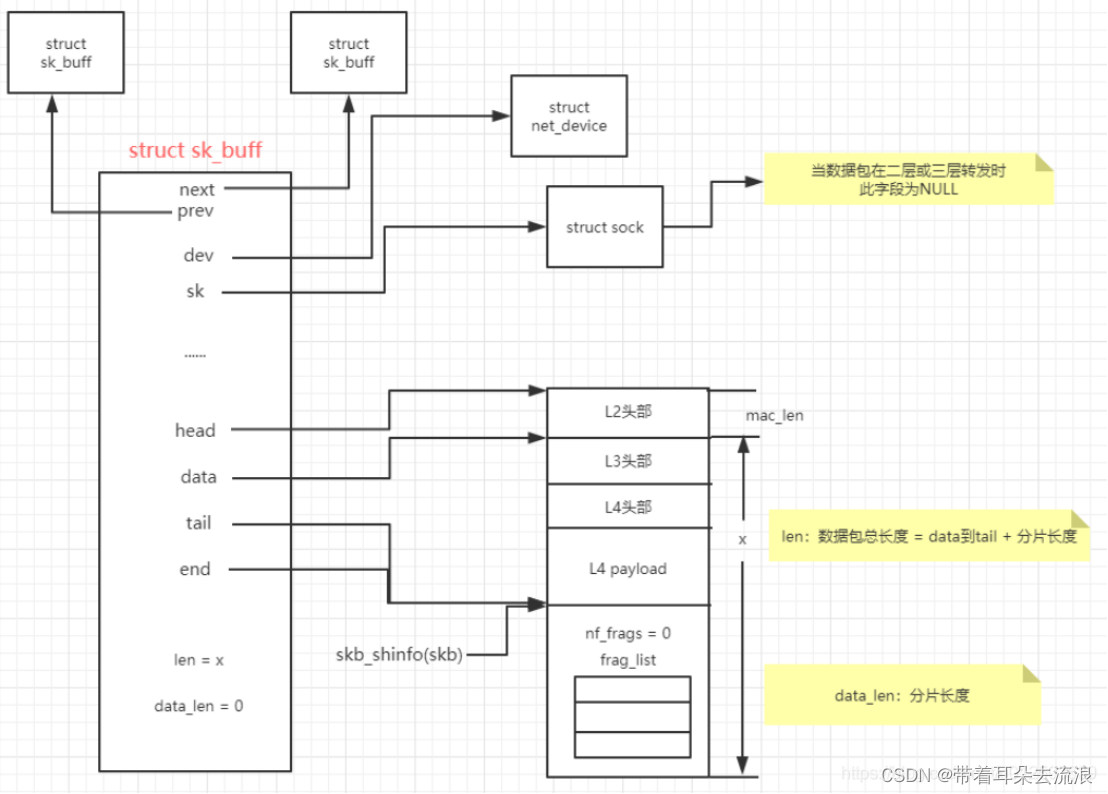
网络数据结构skb_buff原理
skb_buff基本原理 内核中sk_buff结构体在各层协议之间传输不是用拷贝sk_buff结构体,而是通过增加协议头和移动指针来操作的。如果是从L4传输到L2,则是通过往sk_buff结构体中增加该层协议头来操作;如果是从L4到L2,则是通过移动sk_…...
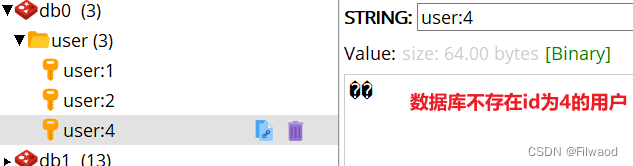
SpringCache使用详解
SpringCache 1.新建测试项目SpringCache2.SpringCache整合redis2.1.Cacheable2.2.CacheEvict2.3.Cacheput2.4.Caching2.5.CacheConfig 3.SpringCache问题4.SpringCache实现多级缓存 1.新建测试项目SpringCache 引入依赖 <dependencies><dependency><groupId&g…...
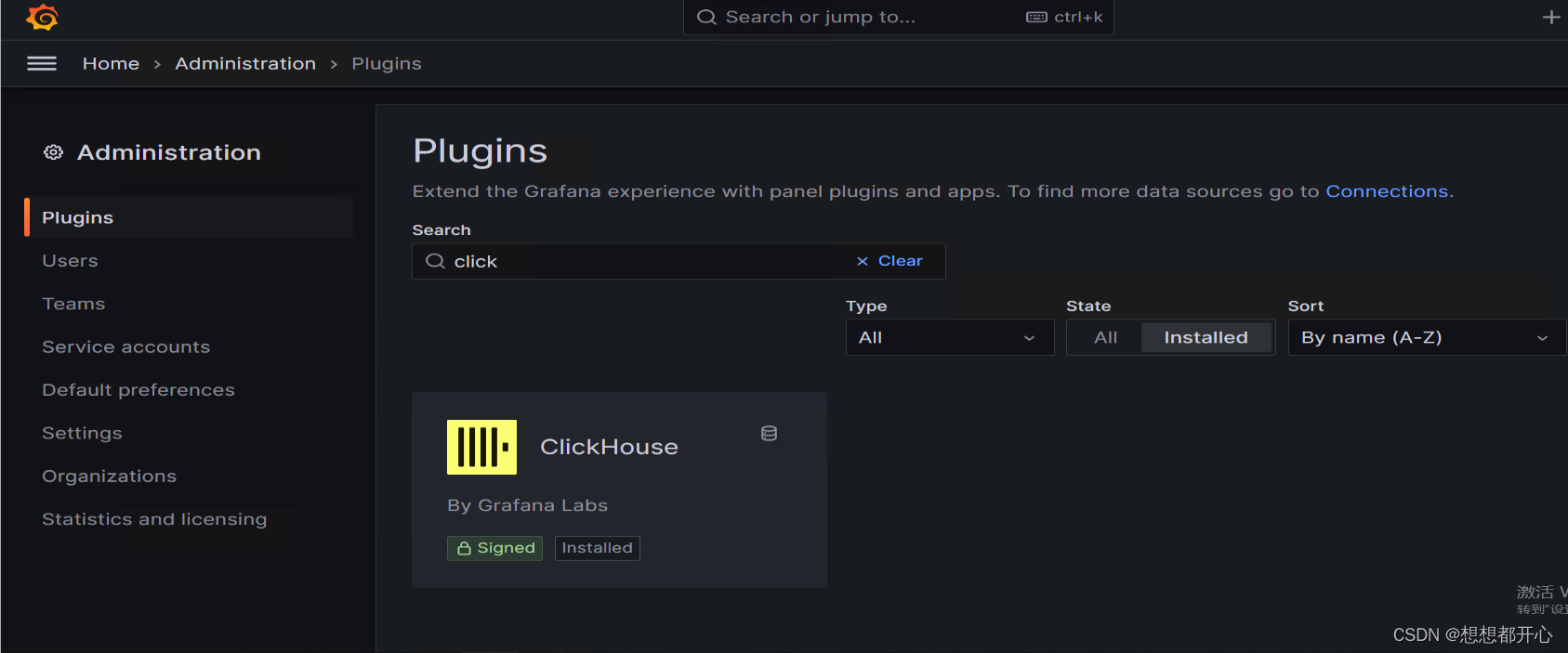
windows版本的grafana如何离线安装插件
本文以安装clickhouse的插件为例,记录下如何离线安装插件 1 下载插件 ClickHouse plugin for Grafana | Grafana Labs 2 找到grafana的配置文件 打开编辑,搜索plugin关键字,修改plugin的加载目录 目录不存在,手动创建࿰…...

ElasticSearch01
ElasticSearch 版本:7.8 学习视频:尚硅谷 笔记:https://zgtsky.top/ ElasticSearch介绍 Elaticsearch,简称为es, es是一个开源的高扩展的分布式全文检索引擎,它可以近乎实时的存储、检索数据;…...

GPT、GPT-2、GPT-3论文精读笔记
视频:GPT,GPT-2,GPT-3 论文精读【论文精读】_哔哩哔哩_bilibili MAE论文:把bert用回计算机视觉领域 CLIP论文:打通文本和图像 GPT 论文:Improving Language Understanding by Generative Pre-Training …...

深度学习八股文:混合精度训练过程出nan怎么办
其实如果是FP32的训练,基本的调试方法还是差不多,这里就讲一下混合精度训练过程中的nan。 混合精度训练使用较低的数值精度(通常是半精度浮点数,例如FP16)来加速模型训练,但在一些情况下,可能会…...

竞赛选题 题目:基于卷积神经网络的手写字符识别 - 深度学习
文章目录 0 前言1 简介2 LeNet-5 模型的介绍2.1 结构解析2.2 C1层2.3 S2层S2层和C3层连接 2.4 F6与C5层 3 写数字识别算法模型的构建3.1 输入层设计3.2 激活函数的选取3.3 卷积层设计3.4 降采样层3.5 输出层设计 4 网络模型的总体结构5 部分实现代码6 在线手写识别7 最后 0 前言…...
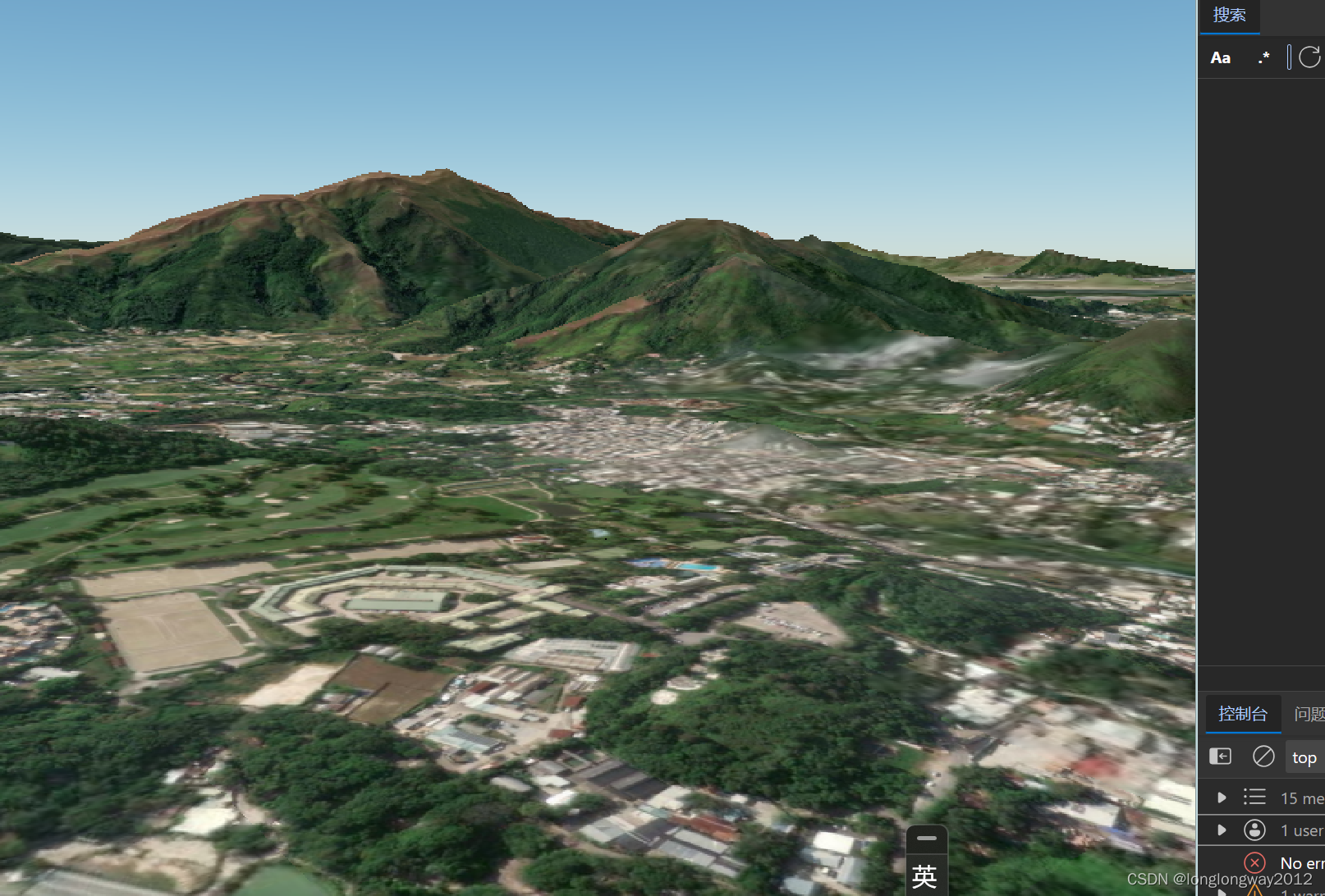
Cesium-terrain-builder编译入坑详解
本以为编译cesium-terrian-tools编译应该没那么难,不想问题重重,不想后人重蹈覆辙,也记录下点点滴滴。 目前网上存在的cesium代码版本主要有两个分支: 原始网站【不能生成layer文件,且经久不更新,使用gdal…...

3.1 CPU内部结构与时钟与指令
CPU内部结构 总线一些自定义部件总线图内存指令执行流程:取指令,译码,执行pc做的事内存地址寄存器内存缓存寄存器指令寄存器,译码第一步指令寄存器传递地址到内存地址寄存器指令MOV_A的过程(译码第二步)第一条指令执行完毕第三条指令的执行第四条指令第四条指令不同的执行流程…...
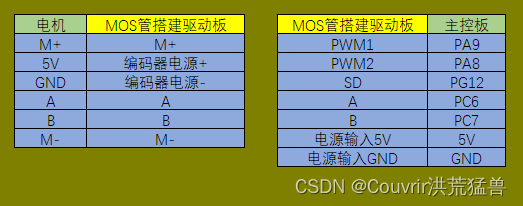
电机应用-直流有刷电机多环控制实现
目录 直流有刷电机多环控制实现 硬件设计 直流电机三环(速度环、电流环、位置环)串级PID控制-位置式PID 编程要点 配置ADC可读取电流值 配置基本定时器6产生定时中断读取当前电路中驱动电机的电流值并执行PID运算 配置定时器1输出PWM控制电机 配…...
)
rknn优化教程(二)
文章目录 1. 前述2. 三方库的封装2.1 xrepo中的库2.2 xrepo之外的库2.2.1 opencv2.2.2 rknnrt2.2.3 spdlog 3. rknn_engine库 1. 前述 OK,开始写第二篇的内容了。这篇博客主要能写一下: 如何给一些三方库按照xmake方式进行封装,供调用如何按…...

React第五十七节 Router中RouterProvider使用详解及注意事项
前言 在 React Router v6.4 中,RouterProvider 是一个核心组件,用于提供基于数据路由(data routers)的新型路由方案。 它替代了传统的 <BrowserRouter>,支持更强大的数据加载和操作功能(如 loader 和…...

QMC5883L的驱动
简介 本篇文章的代码已经上传到了github上面,开源代码 作为一个电子罗盘模块,我们可以通过I2C从中获取偏航角yaw,相对于六轴陀螺仪的yaw,qmc5883l几乎不会零飘并且成本较低。 参考资料 QMC5883L磁场传感器驱动 QMC5883L磁力计…...

基础测试工具使用经验
背景 vtune,perf, nsight system等基础测试工具,都是用过的,但是没有记录,都逐渐忘了。所以写这篇博客总结记录一下,只要以后发现新的用法,就记得来编辑补充一下 perf 比较基础的用法: 先改这…...

Unit 1 深度强化学习简介
Deep RL Course ——Unit 1 Introduction 从理论和实践层面深入学习深度强化学习。学会使用知名的深度强化学习库,例如 Stable Baselines3、RL Baselines3 Zoo、Sample Factory 和 CleanRL。在独特的环境中训练智能体,比如 SnowballFight、Huggy the Do…...

基于SpringBoot在线拍卖系统的设计和实现
摘 要 随着社会的发展,社会的各行各业都在利用信息化时代的优势。计算机的优势和普及使得各种信息系统的开发成为必需。 在线拍卖系统,主要的模块包括管理员;首页、个人中心、用户管理、商品类型管理、拍卖商品管理、历史竞拍管理、竞拍订单…...

JavaScript基础-API 和 Web API
在学习JavaScript的过程中,理解API(应用程序接口)和Web API的概念及其应用是非常重要的。这些工具极大地扩展了JavaScript的功能,使得开发者能够创建出功能丰富、交互性强的Web应用程序。本文将深入探讨JavaScript中的API与Web AP…...

MySQL 主从同步异常处理
阅读原文:https://www.xiaozaoshu.top/articles/mysql-m-s-update-pk MySQL 做双主,遇到的这个错误: Could not execute Update_rows event on table ... Error_code: 1032是 MySQL 主从复制时的经典错误之一,通常表示ÿ…...

go 里面的指针
指针 在 Go 中,指针(pointer)是一个变量的内存地址,就像 C 语言那样: a : 10 p : &a // p 是一个指向 a 的指针 fmt.Println(*p) // 输出 10,通过指针解引用• &a 表示获取变量 a 的地址 p 表示…...

云原生周刊:k0s 成为 CNCF 沙箱项目
开源项目推荐 HAMi HAMi(原名 k8s‑vGPU‑scheduler)是一款 CNCF Sandbox 级别的开源 K8s 中间件,通过虚拟化 GPU/NPU 等异构设备并支持内存、计算核心时间片隔离及共享调度,为容器提供统一接口,实现细粒度资源配额…...
