优化数据分析——理解与运用各类指标
写在开头
数据分析在当今信息时代扮演着至关重要的角色,而指标则是我们理解数据、揭示模式、支持决策的关键工具。本文将深入讨论各类指标的应用场景和解读方法,以帮助更全面、深入地理解数据。
1. 中心趋势指标
1.1 均值:更深层次的理解
均值是数据的平均值,但在实际应用中,我们需注意异常值的影响。例如,在某公司的薪资数据分析中,计算均值时,可能需要排除高管层的高薪数据,以更准确地反映员工的平均收入。
1.2 中位数:抵御偏斜分布
中位数在处理偏斜分布数据时表现更稳健。考虑一家电商公司的订单金额数据,如果存在极高的订单金额,中位数将更好地反映普通订单的典型价值,避免被极端值拉动。
1.3 众数:应对多峰分布
众数在处理多峰分布时具有独特优势。在市场调研中,产品受欢迎程度的众数可以帮助企业更好地了解消费者的偏好,指导产品策略的调整。
2. 离散趋势指标
2.1 标准差:识别离散程度
标准差度量数据的离散程度。考虑一家制造业公司的生产线数据,标准差的增加可能反映了生产过程中的不稳定性,提示可能存在质量控制问题。
2.2 方差:方差背后的故事
方差是标准差的平方,通过了解方差,我们可以更深入地了解数据的波动情况。在股票投资中,高方差可能意味着较大的价格波动,增加了投资的风险。
2.3 四分位间距:探索数据分布的全貌
四分位间距提供了数据分布的四等份划分。在医学研究中,血压数据的四分位间距可以用于评估患者群体的整体血压分布,指导医学干预措施。
3. 形状指标
3.1 偏度:对称与偏斜的平衡
偏度描述数据的对称性。偏度衡量数据分布的对称性,是正态分布的一个重要指标。当偏度为0时,表示数据分布呈现对称;正偏度(偏度大于0)表示数据右侧的尾部更重,负偏度(偏度小于0)表示数据左侧的尾部更重。
考虑一家零售公司,对每月销售额进行偏度分析。如果偏度为正,说明有一些月份销售额较高,可能是由于某种促销活动或季节性效应。相反,如果偏度为负,可能表明存在一些月份销售额较低,需要进一步调查原因。
import pandas as pd# 销售额数据
sales_data = [100, 150, 120, 200, 180, 250, 130, 110, 90, 210]# 计算偏度
skewness = pd.Series(sales_data).skew()print(f"销售额分布的偏度为:{skewness}")
# 值为0.5572816073101072,正偏度。
3.2 峰度:峰值背后的信息
峰度衡量数据分布的尖锐程度,即数据分布相对于正态分布的平峰程度。正态分布的峰度为3,若数据峰度大于3,表示数据分布更陡峭;峰度小于3,表示数据分布较平缓。
考虑气象数据中每日温度变化的峰度。如果峰度较高,表明存在明显的季节性温度波动,例如冬季和夏季温差较大。反之,如果峰度较低,可能是气温相对稳定,属于温和气候。
import pandas as pd# 温度数据
temperature_data = [20, 22, 25, 18, 30, 28, 23, 21, 19, 24]# 计算峰度
kurtosis = pd.Series(temperature_data).kurt()print(f"温度变化数据的峰度为:{kurtosis}")
#值为-0.37942748941857873,小于3,说明数据分布较平缓。
4. 频率指标
4.1 频率:数据分布的生动呈现
频率图和直方图是展现数据分布的强大工具。考虑一家社交媒体平台的用户活跃度数据,通过频率图,我们能够直观地了解不同时间段用户的活跃程度。
4.2 累积频率:洞察数据累积规律
累积频率图有助于观察数据随时间的累积变化。在电商行业,累积购买频率可以帮助企业了解用户留存和回购的趋势,从而制定更有针对性的营销策略。
5. 关联性指标
5.1 相关系数:关系背后的故事
相关系数表达了两个变量之间的线性关系。在广告行业,通过分析广告投放费用与销售额的相关系数,我们能够评估广告投放对销售的实际影响。
5.2 协方差:总体趋势的把握
协方差展示了两个变量的总体趋势。在金融领域,分析股票收益率的协方差可以帮助投资者构建多元化投资组合,降低整体投资风险。
6. 分位数和百分位数
6.1 四分位数:细致刻画数据的分布
通过分析四分位数,我们能更详细地刻画数据的分布情况。四分位数是将数据集按大小分成四等份的值,分别是第一四分位数(Q1)、第二四分位数(Q2,即中位数)、第三四分位数(Q3)以及四分位数范围(IQR = Q3 - Q1)。
在教育领域,学生考试成绩的四分位数可以帮助学校了解不同分数段学生的整体表现,指导教学改进。
import numpy as np# 学生成绩数据
grades = np.array([75, 82, 90, 68, 88, 78, 95, 60, 85, 92])# 计算四分位数
q1 = np.percentile(grades, 25)
q2 = np.percentile(grades, 50)
q3 = np.percentile(grades, 75)
iqr = q3 - q1print(f"第一四分位数 Q1: {q1}")
print(f"中位数 Q2: {q2}")
print(f"第三四分位数 Q3: {q3}")
print(f"四分位数范围 IQR: {iqr}")6.2 百分位数:全面了解数据的位置
百分位数提供了数据中特定位置的百分比信息,例如,第70百分位数表示70%的数据都小于或等于这个值。
在人力资源管理中,员工薪资的百分位数分析可以帮助企业了解员工薪资分布情况,制定公平薪酬政策。
import numpy as np# 薪水数据
salaries = np.array([50000, 55000, 60000, 65000, 70000, 75000, 80000, 85000, 90000, 95000])# 计算第80百分位数
percentile_80 = np.percentile(salaries, 80)print(f"第80百分位数: {percentile_80}")
# 第80百分位数表示80%的员工薪资低于或等于这个值(86000)。7. 概率指标
7.1 概率:决策支持的重要依据
概率是决策制定的基础。考虑一个电信运营商,通过分析客户流失的概率,公司可以制定相应的客户保留策略,提高客户忠诚度。又或者一家电商公司根据历史数据分析得出,某个特定广告点击后用户最终购买的概率为0.3。这个概率值可以用来制定营销策略,例如决定在该广告上投放更多资源,因为有30%的概率用户会购买。
7.2 条件概率:精准决策的关键
条件概率提供了在给定条件下事件发生的概率。在医学研究中,通过分析某种疾病在不同年龄段的发病率,可以帮助医生更精准地进行年龄相关的疾病预防工作。
例如,考虑一种医学筛查测试,测试的准确率为0.9,而患病的先验概率为0.05。那么,在测试呈阳性的条件下,患病的条件概率可以通过贝叶斯定理计算,提供更准确的诊断信息。这里举一个例子,如下:
| 患病 | 未患病 | |
|---|---|---|
| 检测出 | 90 | 1710 |
| 未检测出 | 10 | 190 |
准确率=检测正确人数 / 总人数=1800/2000=0.9
患病先验概率 = 患病人数 / 总人数 = 100 / 2000 = 0.05
若用A表示患病率,则 P ( A ) = 0.05 P(A) =0.05 P(A)=0.05
用B表示测试出阳性(患病)的概率,则 P ( B ) = 测试阳性 ( 患病 ) 的人数 / 总人数 = ( 90 + 190 ) / 2000 = 0.14 P(B) = 测试阳性(患病)的人数/总人数 = (90 + 190)/2000 = 0.14 P(B)=测试阳性(患病)的人数/总人数=(90+190)/2000=0.14
那么对于检测出阳性中,真实患病的概率为:
P ( A ∣ B ) = P ( A ⋂ B ) / P ( B ) = P ( 患病且测试呈阳性的人数 ) / P ( 测试出阳性的概率 ) = 90 2000 280 2000 = 0.3214 P(A\mid B)=P(A\bigcap B) / P(B) = P(患病且测试呈阳性的人数)/P(测试出阳性的概率) = {{90\over2000} \over {280\over 2000}}= 0.3214 P(A∣B)=P(A⋂B)/P(B)=P(患病且测试呈阳性的人数)/P(测试出阳性的概率)=2000280200090=0.3214
那么对于患病情况下,检测呈现阳性的概率为:
P ( B ∣ A ) = P ( A ⋂ B ) / P ( A ) = P ( 患病且测试呈阳性的人数 ) / P ( 患病率 ) = 90 2000 100 2000 = 90 / 100 = 0.9 P(B\mid A) = P(A\bigcap B) / P(A) = P(患病且测试呈阳性的人数)/P(患病率) = {{90\over2000} \over {100\over 2000}} = 90/100 = 0.9 P(B∣A)=P(A⋂B)/P(A)=P(患病且测试呈阳性的人数)/P(患病率)=2000100200090=90/100=0.9
P ( B ∣ A ) = P ( A ∣ B ) ∗ P ( B ) / P ( A ) = 0.3214 ∗ 0.14 0.05 = 0.90 P(B\mid A) = P(A\mid B) *P(B) / P(A) = {{0.3214 * 0.14} \over {0.05}} = 0.90 P(B∣A)=P(A∣B)∗P(B)/P(A)=0.050.3214∗0.14=0.90
8. 效能指标
8.1 准确率:综合评估模型性能
准确率是模型整体性能的综合评估指标。在电商行业,通过分析推荐系统的准确率,可以评估系统是否能够准确推荐符合用户兴趣的产品。
8.2 精确度、召回率、F1分数:深度解析模型性能
通过深入解析这些效能指标,在医学图像识别领域,分析模型的精确度、召回率和F1分数,有助于评估模型对病灶的检测效果,指导医生的临床决策。
考虑一个医学图像识别模型,用于检测肿瘤。在这个场景中,精确度(Precision)是指模型识别出的肿瘤图像中,真正是肿瘤的比例。召回率(Recall)是指实际肿瘤图像中,被模型正确识别出来的比例。F1分数综合了精确度和召回率,是一个综合性的性能指标,特别适用于处理不均衡数据集,其中正例(肿瘤)相对较少。
from sklearn.metrics import precision_score, recall_score, f1_score# 医学图像识别结果
true_labels = [1, 0, 1, 1, 0, 1, 0, 1, 1, 1] # 真实标签,1表示肿瘤存在
predicted_labels = [1, 0, 1, 0, 0, 1, 1, 1, 1, 0] # 模型预测的标签# 计算精确度、召回率和F1分数
precision = precision_score(true_labels, predicted_labels)
recall = recall_score(true_labels, predicted_labels)
f1 = f1_score(true_labels, predicted_labels)print(f"精确度: {precision}")
print(f"召回率: {recall}")
print(f"F1分数: {f1}")9. 时间序列指标
9.1 移动平均:平滑趋势
移动平均是通过计算一系列连续子集的平均值来平滑时间序列数据,以便更清晰地观察趋势。
例子:销售额趋势分析
假设我们有一家公司的月度销售额数据:
import pandas as pd# 销售额数据
sales_data = {'Month': ['Jan', 'Feb', 'Mar', 'Apr', 'May', 'Jun'],'Sales': [100, 120, 80, 110, 90, 130]}
df = pd.DataFrame(sales_data)# 计算3个月的移动平均
df['Moving_Avg'] = df['Sales'].rolling(window=3).mean()print(df)
通过计算3个月的移动平均,我们可以更清楚地看到销售额的趋势,有助于预测未来的销售情况。
9.2 时间序列分解:趋势、季节和残差
时间序列分解将时间序列数据分解为趋势、季节性和残差三个部分,以更深入地了解其组成成分。
例子:气温变化分析
考虑每日气温的时间序列数据:
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from statsmodels.tsa.seasonal import seasonal_decompose# 气温变化数据
temperature_data = {'Date': pd.date_range(start='2022-01-01', periods=365 *2, freq='D'),'Temperature': np.sin(np.linspace(0, 2*np.pi, 365 * 2)) * 10 + 25}# print(len(temperature_data['Temperature']))
df_temperature = pd.DataFrame(temperature_data)
df_temperature.set_index('Date', inplace=True)# 进行时间序列分解
result = seasonal_decompose(df_temperature['Temperature'], model='additive', period=365)# 可视化分解结果
result.plot()
plt.show()
通过分解,我们可以清楚地看到气温变化中的趋势、季节性和残差,有助于深入了解气温的变化规律。
10. 经济学指标
10.1 GDP、通货膨胀率、失业率:国家经济健康的晴雨表
在政府决策中,通过深入了解国家的GDP、通货膨胀率和失业率,可以更全面地评估经济健康状况,为宏观经济政策的制定提供支持。
11. 风险指标
11.1 Value at Risk (VaR):风险价值
VaR是一个用于度量投资组合或资产风险的指标,表示在一定置信水平下,投资可能遭受的最大损失。
例子:金融投资组合风险评估
考虑一个投资组合,我们可以使用VaR来衡量在一定置信水平(例如95%)下,该投资组合可能的最大损失。这有助于投资者更好地理解潜在的风险和损失水平。
import numpy as np# 投资组合收益率数据
returns = np.random.normal(0.001, 0.02, 1000)# 计算95% VaR
var_95 = np.percentile(returns, 5)print(f"95% VaR: {var_95}")
11.2 Conditional Value at Risk (CVaR):条件风险价值
CVaR是在VaR基础上,对超出VaR水平的损失进行平均的指标,更全面地反映了极端情况下的风险。
例子:能源市场风险管理
在能源市场中,CVaR可以用来评估在不同价格波动情况下,电力公司面临的损失风险。通过计算CVaR,公司可以更全面地了解在不同市场条件下可能发生的损失水平。
import numpy as np# 电力公司收益率数据
returns_energy = np.random.normal(0.001, 0.03, 1000)# 计算95% VaR
var_95 = np.percentile(returns_energy, 5)# 计算95% CVaR
cvar_95 = np.mean(returns_energy[returns_energy <= var_95])print(f"95% VaR: {var_95}")
print(f"95% CVaR: {cvar_95}")写在最后
对各类指标的深入探讨,我们能够更全面、精准地理解数据。在实际数据分析过程中,不仅要熟练掌握这些指标的计算方法,更需要结合实际业务场景,深入思考每个指标背后所蕴含的意义。数据分析不仅仅是冷冰冰的数字堆积,更是对现象背后规律的深刻理解,是对数据故事的讲述。
在未来的数据分析工作中,我们应该注重对不同指标之间的关联性、交叉影响的分析。同时,结合可视化工具,将抽象的数据指标转化为更具直观感受的图形,能够更生动地呈现数据的特征,为决策者提供更直观的决策支持。
最终,深入理解各类指标,善于在实际应用中灵活运用,将使我们在数据分析的道路上更进一步,为业务的持续发展提供更加可靠和深刻的支持。
相关文章:

优化数据分析——理解与运用各类指标
写在开头 数据分析在当今信息时代扮演着至关重要的角色,而指标则是我们理解数据、揭示模式、支持决策的关键工具。本文将深入讨论各类指标的应用场景和解读方法,以帮助更全面、深入地理解数据。 1. 中心趋势指标 1.1 均值:更深层次的理解 …...
)
JS实现数字千分位分割(手写纯享版)
简介 在前端开发中,我们经常需要对数字进行格式化,其中一种常见的需求就是将数字表示为千分位格式,以提高可读性。本文将介绍如何使用 JavaScript 实现一个简单而有效的千分位格式化函数。 千分位格式化的需求 千分位格式化是一种将数字中…...

入门指南:介绍Python库——Pandas
个人网站 本文首发于公众号小肖学数据分析 Pandas是一个功能强大、灵活易用的Python数据处理库。 无论你是数据分析师、数据科学家还是Python初学者,掌握Pandas都将为你提供高效、便捷的数据处理和分析能力。 本文将为你详细介绍Pandas的基本概念、常用功能和使…...
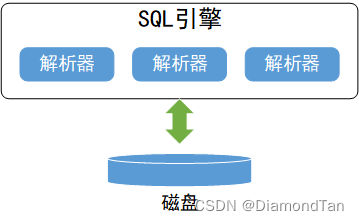
数据库语句执行流程(查询原理)SQL
SQL作为一种数据库编程语言,其执行过程大致为,终端上输入SQL语句 会传输到数据库服务器,然后SQL语句在服务器内经过解析器的检查和翻译,优化器的执行效率提升,在执行器中通过存储引擎提供的数据给出结果。详细过程如下…...

FileReader与URL.createObjectURL实现图片、视频上传预览
之前做图片、视频上传预览常用的方案是先把文件上传到服务器,等服务器返回文件的地址后,再把该地址字符串赋给img或video的src属性,这才实现所谓的文件预览。实际上这只是文件“上传后再预览”,这既浪费了用户的时间,也…...
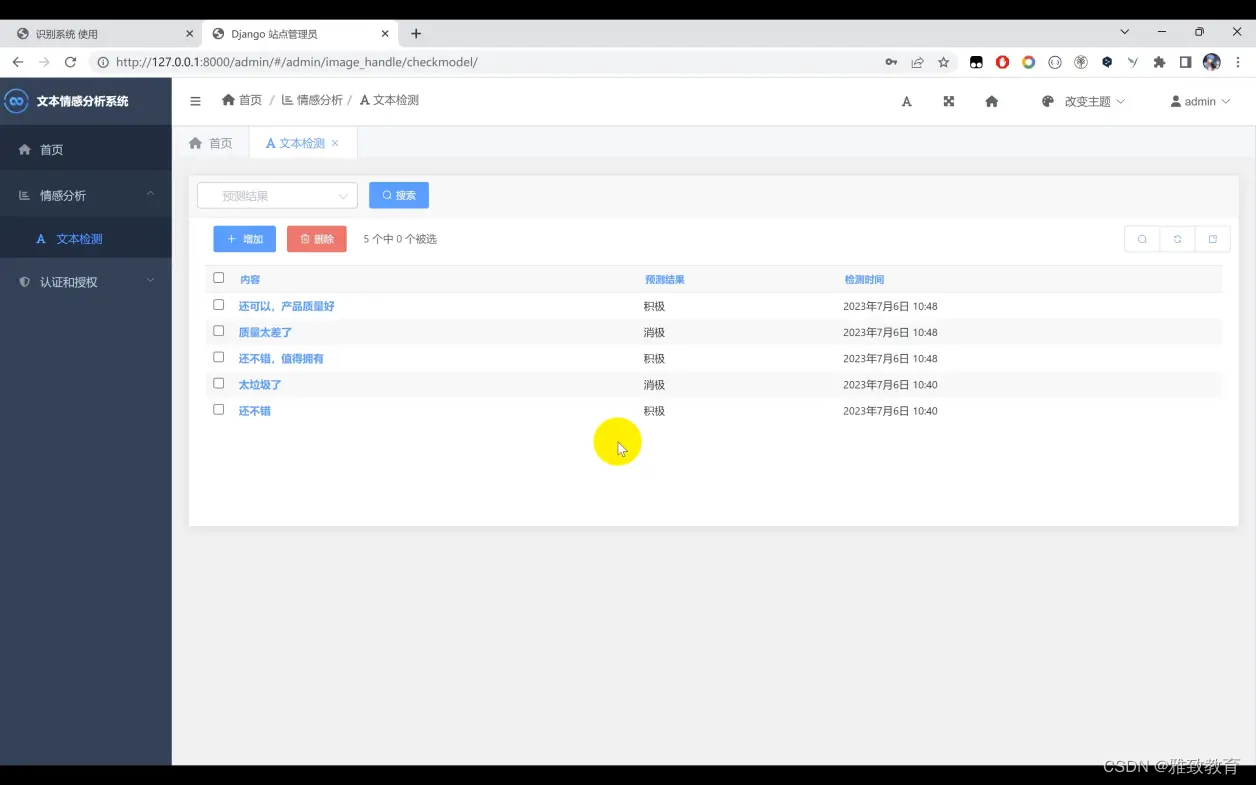
基于python+Django+SVM算法模型的文本情感识别系统
欢迎大家点赞、收藏、关注、评论啦 ,由于篇幅有限,只展示了部分核心代码。 文章目录 一项目简介1. 简介2. 技术栈3. 系统架构4. 关键模块介绍5. 如何运行 二、功能三、系统四. 总结 一项目简介 # 基于 Python Django SVM 算法模型的文本情感识别系统介…...

数据结构之栈与队列习题详解解析
个人主页:点我进入主页 专栏分类:C语言初阶 C语言程序设计————KTV C语言小游戏 C语言进阶 C语言刷题 数据结构初阶 欢迎大家点赞,评论,收藏。 一起努力,一起奔赴大厂。 目录 1.前言 2.概念题…...
C++ 动态规划 DP教程 (一)思考过程(*/ω\*)
动态规划是一种思维方法,大家首先要做的就是接受这种思维方法,认同他,然后再去运用它解决新问题。 动态规划是用递推的思路去解决问题。 首先确定问题做一件什么事情? 对这件事情分步完成,分成很多步。 如果我们把整件…...
】文件和异常详解:使用、读取、写入、追加、保存用户的信息,以及优雅的处理异常)
【python基础(九)】文件和异常详解:使用、读取、写入、追加、保存用户的信息,以及优雅的处理异常
文章目录 一. 从文件中读取数据1. 读取整个文件2. 文件路径3. 逐行读取4. 创建一个包含文件各行内容的列表 二. 写入文件1. 写入空文件2. 写入多行3. 附加到文件 三. 异常1. 处理ZeroDivisionError异常2. 使用try-except代码块3. try-except-else ing4. 处理FileNotFoundError异…...

详解C语言中的指针数组和数组指针
指针数组和数组指针是 C 语言中比较常见的两种类型。它们虽然名字很相似,但是含义、用法以及指向类型都不同,需要分开理解。 指针数组 指针数组是一个数组,其中每个元素都是一个指针。这些指针可以指向不同类型的数据,也可以指向…...

【done】剑指offer18:删除链表指定节点
力扣,https://leetcode.cn/problems/shan-chu-lian-biao-de-jie-dian-lcof/description/ // 自己写的答案 class Solution {public ListNode deleteNode(ListNode head, int val) {if (head null) {return null;}if (head.val val) {return head.next;}ListNode …...

图形编辑器开发:缩放和旋转控制点
大家好,我是前端西瓜哥。好久没写图形编辑器开发的文章了。 今天来讲讲控制点。它是图形编辑器的不可缺少的基础功能。 控制点是吸附在图形上的一些小矩形和圆形点击区域,在控制点上拖拽鼠标,能够实时对被选中进行属性的更新。 比如使用旋…...
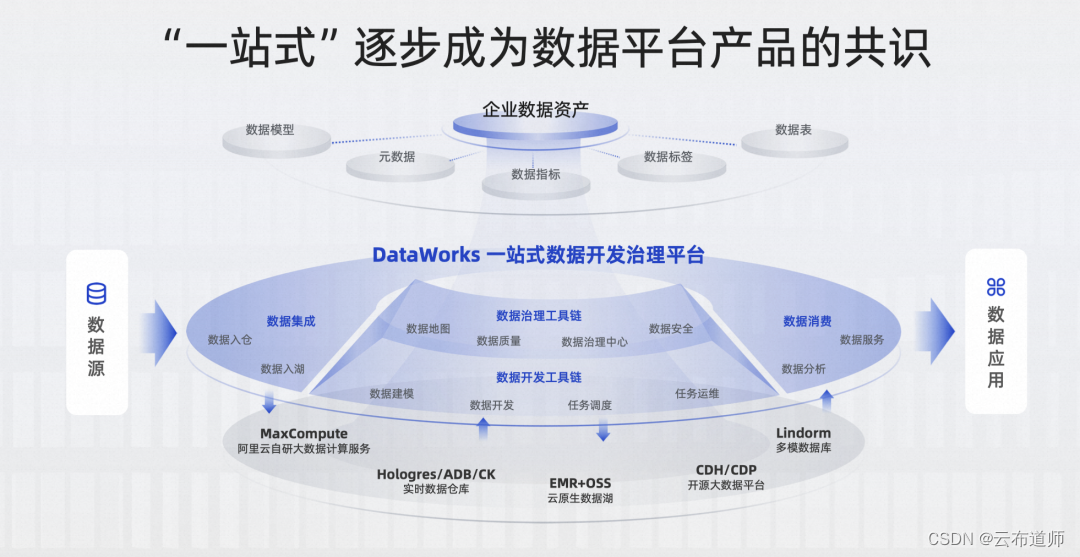
【2023 云栖】阿里云田奇铣:大模型驱动 DataWorks 数据开发治理平台智能化升级
云布道师 本文根据 2023 云栖大会演讲实录整理而成,演讲信息如下: 演讲人:田奇铣 | 阿里云 DataWorks 产品负责人 演讲主题:大模型驱动 DataWorks 数据开发治理平台智能化升级 随着大模型掀起 AI 技术革新浪潮,大数…...
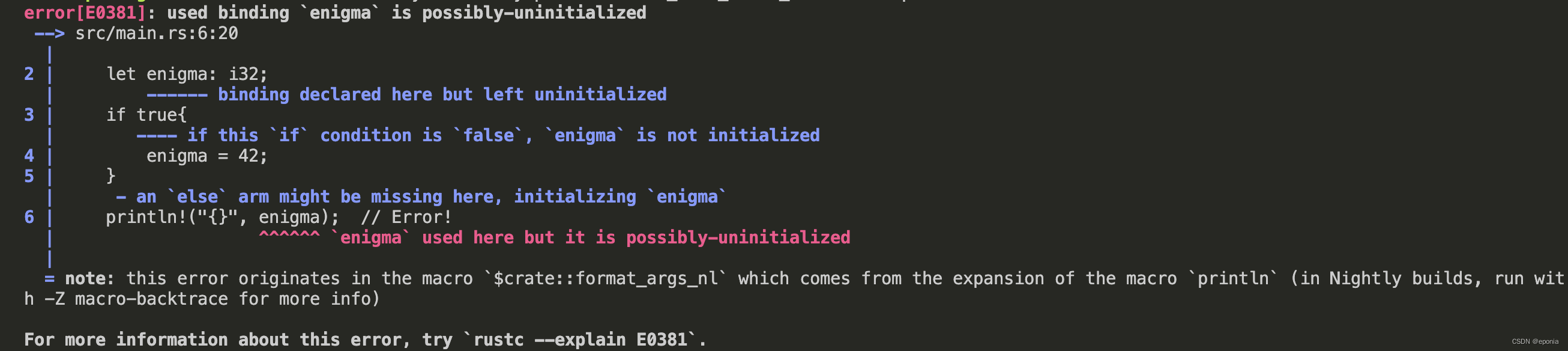
Rust语言入门教程(二) - 变量与作用域
变量与作用域 变量的声明与初始化 Rust的基本语法格式如下: fn main(){let bunnies 2; }语句以分号结尾,用花括号包含语句块。 Rust的语法其实借鉴了很多其他的语言,比如C语言和Python, 所以变量定义的格式看起来也跟很多我们…...

芯知识 | Flash可更换声音语音芯片—引领音频IC技术革新的新篇章
随着科技的飞速发展,人们对于电子产品的音频性能要求越来越高。在这种背景下,Flash可更换声音语音芯片应运而生,成为音频技术领域的一颗璀璨明星。本文将详细介绍Flash可更换声音语音芯片的特点、优势以及应用场景,展望其在未来科…...

合共软件创新亮相:第102届上海电子展成就技术新篇章
2023年,第102届中国(上海)电子展活动在全球瞩目中圆满落幕。作为下半年华东地区最具影响力的电子展会,此次盛会吸引了来自全球的600家领先企业,共同探讨电子元器件行业的最新发展成果和趋势。 本届展会围绕核心先导元器…...

Ubuntu20.04清理垃圾vscode缓存
使用VM虚拟机安装了Ubuntu系统,主目录空间越来越小,硬盘扩容之后很快又空间不足,甚至出现了开机卡黑屏的情况,这里记录一下解决过程。 1 重新开机进入系统 状态:卡到了开机黑屏状态,左上角有一条小横杠 原…...
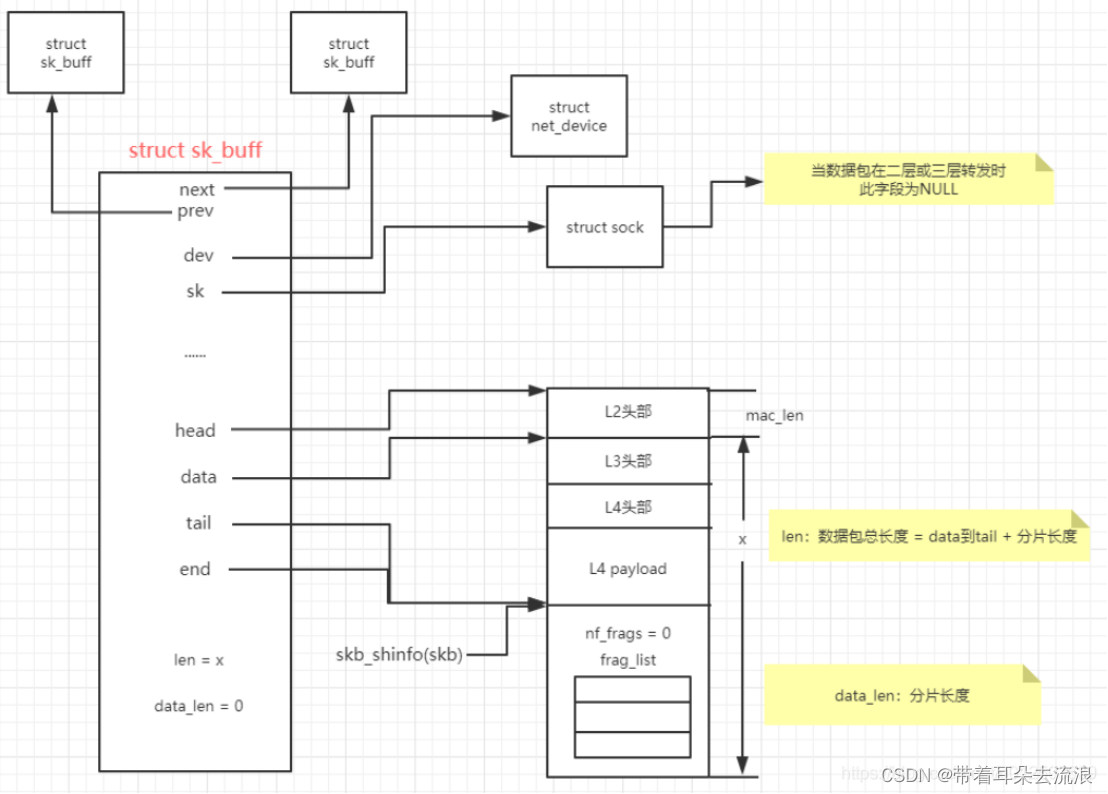
网络数据结构skb_buff原理
skb_buff基本原理 内核中sk_buff结构体在各层协议之间传输不是用拷贝sk_buff结构体,而是通过增加协议头和移动指针来操作的。如果是从L4传输到L2,则是通过往sk_buff结构体中增加该层协议头来操作;如果是从L4到L2,则是通过移动sk_…...
SpringCache使用详解
SpringCache 1.新建测试项目SpringCache2.SpringCache整合redis2.1.Cacheable2.2.CacheEvict2.3.Cacheput2.4.Caching2.5.CacheConfig 3.SpringCache问题4.SpringCache实现多级缓存 1.新建测试项目SpringCache 引入依赖 <dependencies><dependency><groupId&g…...
windows版本的grafana如何离线安装插件
本文以安装clickhouse的插件为例,记录下如何离线安装插件 1 下载插件 ClickHouse plugin for Grafana | Grafana Labs 2 找到grafana的配置文件 打开编辑,搜索plugin关键字,修改plugin的加载目录 目录不存在,手动创建࿰…...

苍穹外卖--缓存菜品
1.问题说明 用户端小程序展示的菜品数据都是通过查询数据库获得,如果用户端访问量比较大,数据库访问压力随之增大 2.实现思路 通过Redis来缓存菜品数据,减少数据库查询操作。 缓存逻辑分析: ①每个分类下的菜品保持一份缓存数据…...
)
【服务器压力测试】本地PC电脑作为服务器运行时出现卡顿和资源紧张(Windows/Linux)
要让本地PC电脑作为服务器运行时出现卡顿和资源紧张的情况,可以通过以下几种方式模拟或触发: 1. 增加CPU负载 运行大量计算密集型任务,例如: 使用多线程循环执行复杂计算(如数学运算、加密解密等)。运行图…...

【数据分析】R版IntelliGenes用于生物标志物发现的可解释机器学习
禁止商业或二改转载,仅供自学使用,侵权必究,如需截取部分内容请后台联系作者! 文章目录 介绍流程步骤1. 输入数据2. 特征选择3. 模型训练4. I-Genes 评分计算5. 输出结果 IntelliGenesR 安装包1. 特征选择2. 模型训练和评估3. I-Genes 评分计…...

代码随想录刷题day30
1、零钱兑换II 给你一个整数数组 coins 表示不同面额的硬币,另给一个整数 amount 表示总金额。 请你计算并返回可以凑成总金额的硬币组合数。如果任何硬币组合都无法凑出总金额,返回 0 。 假设每一种面额的硬币有无限个。 题目数据保证结果符合 32 位带…...

LINUX 69 FTP 客服管理系统 man 5 /etc/vsftpd/vsftpd.conf
FTP 客服管理系统 实现kefu123登录,不允许匿名访问,kefu只能访问/data/kefu目录,不能查看其他目录 创建账号密码 useradd kefu echo 123|passwd -stdin kefu [rootcode caozx26420]# echo 123|passwd --stdin kefu 更改用户 kefu 的密码…...

【C++进阶篇】智能指针
C内存管理终极指南:智能指针从入门到源码剖析 一. 智能指针1.1 auto_ptr1.2 unique_ptr1.3 shared_ptr1.4 make_shared 二. 原理三. shared_ptr循环引用问题三. 线程安全问题四. 内存泄漏4.1 什么是内存泄漏4.2 危害4.3 避免内存泄漏 五. 最后 一. 智能指针 智能指…...

CSS | transition 和 transform的用处和区别
省流总结: transform用于变换/变形,transition是动画控制器 transform 用来对元素进行变形,常见的操作如下,它是立即生效的样式变形属性。 旋转 rotate(角度deg)、平移 translateX(像素px)、缩放 scale(倍数)、倾斜 skewX(角度…...

什么是VR全景技术
VR全景技术,全称为虚拟现实全景技术,是通过计算机图像模拟生成三维空间中的虚拟世界,使用户能够在该虚拟世界中进行全方位、无死角的观察和交互的技术。VR全景技术模拟人在真实空间中的视觉体验,结合图文、3D、音视频等多媒体元素…...

【UE5 C++】通过文件对话框获取选择文件的路径
目录 效果 步骤 源码 效果 步骤 1. 在“xxx.Build.cs”中添加需要使用的模块 ,这里主要使用“DesktopPlatform”模块 2. 添加后闭UE编辑器,右键点击 .uproject 文件,选择 "Generate Visual Studio project files",重…...
:LeetCode 142. 环形链表 II(Linked List Cycle II)详解)
Java详解LeetCode 热题 100(26):LeetCode 142. 环形链表 II(Linked List Cycle II)详解
文章目录 1. 题目描述1.1 链表节点定义 2. 理解题目2.1 问题可视化2.2 核心挑战 3. 解法一:HashSet 标记访问法3.1 算法思路3.2 Java代码实现3.3 详细执行过程演示3.4 执行结果示例3.5 复杂度分析3.6 优缺点分析 4. 解法二:Floyd 快慢指针法(…...
