LeetCode 2304. 网格中的最小路径代价:DP
【LetMeFly】2304.网格中的最小路径代价:DP
力扣题目链接:https://leetcode.cn/problems/minimum-path-cost-in-a-grid/
给你一个下标从 0 开始的整数矩阵 grid ,矩阵大小为 m x n ,由从 0 到 m * n - 1 的不同整数组成。你可以在此矩阵中,从一个单元格移动到 下一行 的任何其他单元格。如果你位于单元格 (x, y) ,且满足 x < m - 1 ,你可以移动到 (x + 1, 0), (x + 1, 1), ..., (x + 1, n - 1) 中的任何一个单元格。注意: 在最后一行中的单元格不能触发移动。
每次可能的移动都需要付出对应的代价,代价用一个下标从 0 开始的二维数组 moveCost 表示,该数组大小为 (m * n) x n ,其中 moveCost[i][j] 是从值为 i 的单元格移动到下一行第 j 列单元格的代价。从 grid 最后一行的单元格移动的代价可以忽略。
grid 一条路径的代价是:所有路径经过的单元格的 值之和 加上 所有移动的 代价之和 。从 第一行 任意单元格出发,返回到达 最后一行 任意单元格的最小路径代价。
示例 1:

输入:grid = [[5,3],[4,0],[2,1]], moveCost = [[9,8],[1,5],[10,12],[18,6],[2,4],[14,3]] 输出:17 解释:最小代价的路径是 5 -> 0 -> 1 。 - 路径途经单元格值之和 5 + 0 + 1 = 6 。 - 从 5 移动到 0 的代价为 3 。 - 从 0 移动到 1 的代价为 8 。 路径总代价为 6 + 3 + 8 = 17 。
示例 2:
输入:grid = [[5,1,2],[4,0,3]], moveCost = [[12,10,15],[20,23,8],[21,7,1],[8,1,13],[9,10,25],[5,3,2]] 输出:6 解释: 最小代价的路径是 2 -> 3 。 - 路径途经单元格值之和 2 + 3 = 5 。 - 从 2 移动到 3 的代价为 1 。 路径总代价为 5 + 1 = 6 。
提示:
m == grid.lengthn == grid[i].length2 <= m, n <= 50grid由从0到m * n - 1的不同整数组成moveCost.length == m * nmoveCost[i].length == n1 <= moveCost[i][j] <= 100
方法一:DP
从倒数第二行开始往第一行遍历:
- 对于这一行的每一个元素:
- 计算出 从下一行的所有元素中来到这一行,增加值最小的那个
- 这个元素加上下一行来的最小增加量
最终返回第一行中的最小元素即为答案。
- 时间复杂度 O ( n m 2 ) O(nm^2) O(nm2),其中 s i z e ( g r i d ) = n × m size(grid)=n\times m size(grid)=n×m( n n n行 m m m列)
- 空间复杂度 O ( 1 ) O(1) O(1)
AC代码
C++
class Solution {
public:int minPathCost(vector<vector<int>>& grid, vector<vector<int>>& moveCost) {int n = grid.size(), m = grid[0].size();for (int i = n - 2; i >= 0; i--) {for (int j = 0; j < m; j++) {int m_ = 100000000;for (int k = 0; k < m; k++) {m_ = min(m_, grid[i + 1][k] + moveCost[grid[i][j]][k]);}grid[i][j] += m_;}}return *min_element(grid[0].begin(), grid[0].end());}
};
Python
# from typing import Listclass Solution:def minPathCost(self, grid: List[List[int]], moveCost: List[List[int]]) -> int:n, m = len(grid), len(grid[0])for i in range(n - 2, -1, -1):for j in range(m):m_ = 100000000for k in range(m):m_ = min(m_, grid[i + 1][k] + moveCost[grid[i][j]][k])grid[i][j] += m_return min(grid[0])同步发文于CSDN,原创不易,转载经作者同意后请附上原文链接哦~
Tisfy:https://letmefly.blog.csdn.net/article/details/134563145
相关文章:

LeetCode 2304. 网格中的最小路径代价:DP
【LetMeFly】2304.网格中的最小路径代价:DP 力扣题目链接:https://leetcode.cn/problems/minimum-path-cost-in-a-grid/ 给你一个下标从 0 开始的整数矩阵 grid ,矩阵大小为 m x n ,由从 0 到 m * n - 1 的不同整数组成。你可以…...

c 实用化的文本终端实时显示摄像头视频
因为采用yuv格式,帧率都很低。图像会拖影。把图像尺寸尽量缩小,能大大改善。现在最麻烦的是图像上有黑色的闪影,不知是为啥?如是framebuffer引起的就无解了。终于找到问题了,是在显示前加了一条用黑色清屏造成的&#…...

CSS中常用的伪类选择器
一 、伪类(不存在的类,特殊的类) -伪类用来描述一个元素的特殊状态 比如:第一个元素,被点击的元素,鼠标移入的元素 -特点:一般请情况下,使用:开头 1、 :first-child …...

【python学习】中级篇-数据库操作:SQLite
SQLite是一个轻量级的数据库引擎,它可以嵌入到各种应用程序中。以下是SQLite的基本用法: 创建数据库文件 import sqlite3# 连接到一个不存在的数据库文件,如果文件不存在,将会自动创建一个新的数据库文件 conn sqlite3.connect…...

汇编-PROTO声明过程
64位汇编 64 模式中,PROTO 伪指令指定程序的外部过程,示例如下: ExitProcess PROTO ;指定外部过程,不需要参数.code main PROCmov ebx, 0FFFFFFFFh mov ecx,0 ;结束程序call ExitProcess ;调用外部过程main ENDP END 32位…...

MYSQL事务操作
...
自动化测试——自动卸载软件
📢专注于分享软件测试干货内容,欢迎点赞 👍 收藏 ⭐留言 📝 如有错误敬请指正!📢交流讨论:欢迎加入我们一起学习!📢资源分享:耗时200小时精选的「软件测试」资…...
)
Linux - 系统调用(syscall)
说明 基于riscv64 soc linux_5.10.4平台,通过新增一个系统调用深入了解下系统调用实现原理。 简介 Linux 软件运行环境分为用户空间和内核空间,默认情况下,用户进程无法访问内核,既不能访问内核所在的内存空间,也不…...

c语言-冒泡排序
冒泡排序原理: 冒泡排序是一种简单直观的排序算法,它重复地遍历待排序的元素序列,比较相邻的两个元素,如果它们的顺序不符合要求(例如升序要求前面的元素小于后面的元素),则交换它们的位置。遍历…...

Mysql面经
Select语句的执行顺序 1、from 子句组装来自不同数据源的数据; 2、where 子句基于指定的条件对记录行进行筛选; 3、group by 子句将数据划分为多个分组; 4、使用聚集函数进行计算;AVG() SUM() MAX() MIN() COUNT() 5、使用 havin…...

1panel可视化Docker面板安装与使用
官网地址1Panel - 现代化、开源的 Linux 服务器运维管理面板 文章目录 目录 文章目录 前言 一、环境准备 二、使用步骤 1.安装命令 2.一些命令 3.使用 总结 前言 一、环境准备 虚拟机centos 已经安装好docker和 Docker Compose 或者都没安装 1panel会帮你自动安装 二、使用…...

es6中的import导入模块 和 export导出模块
es6中的import导入模块 和 export导出模块 一、定义二、使用1.默认导出导入2..命名导出导入3.命名导出(Named Export)与默认导出(Default Export)结合使用 三、总结 一、定义 功能:用于导入和导出模块的内容。 静态加载…...
)
WordPress插件开发教程手册 — 钩子(Hooks)
钩子是用一段代码添加/修改另外一段代码的方式,是 WordPress插件和主题与 WordPress 内核交互的基础,钩子在 WordPress 内核中也被广泛使用。WordPress 中有两种钩子,Action 和 Filter。使用钩子时,我们需要先编写一个自定义函数作…...

Python开发运维:Celery连接Redis
目录 一、理论 1.Celery 二、实验 1.Windows11安装Redis 2.Python3.8环境中配置Celery 3.celery的多目录结构异步执行 4.celery简单结构下的定时任务 三、问题 1.Celery命令报错 2.执行Celery命令报错 3.Win11启动Celery报ValueErro错误 4.Pycharm 无法 import 同目…...
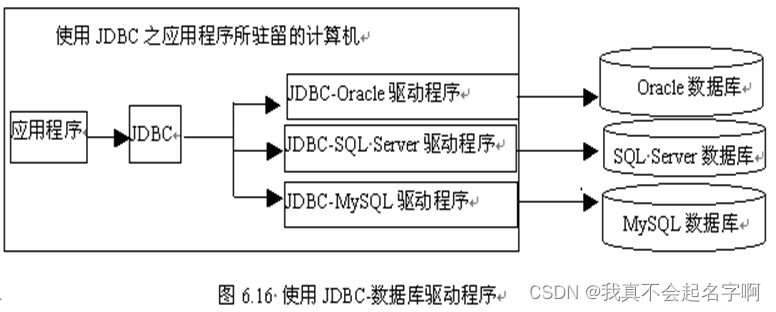
JSP:JDBC
JDBC(Java Data Base Connectivity的缩写)是Java程序操作数据库的API,也是Java程序与数据库相交互的一门技术。 JDBC是Java操作数据库的规范,由一组用Java语言编写的类和接口组成,它对数据库的操作提供基本方法&#…...

能否在一台电脑上安全地登录多个Facebook账号?
Facebook是一个流量大、用户多的平台,许多人可能需要在一台设备上管理多个Facebook账号,无论是出于个人或职业需求,都能带来极大地便利。然而,保持每个账号的安全性和隐私性却是一个挑战。本文将介绍如何在一台电脑上安全地登录多…...
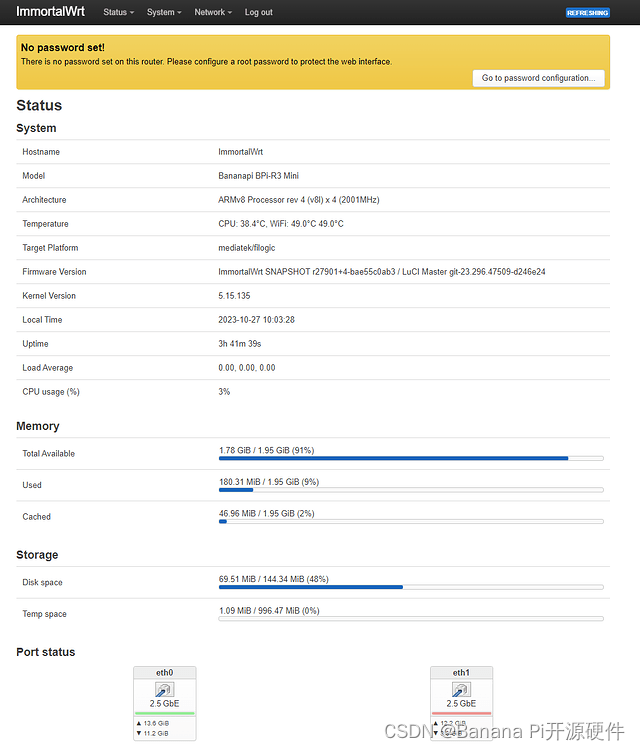
Banana Pi [BPi-R3-Mini] 回顾和主线 ImmortalWrt 固件支持
BananaPi BPi-R3 Mini 采用 MediaTek 830(4 个 A53,最高 2.0 GHz),具有 2 个 2.5 GbE、AX4200 2.4G/5G 无线和 USB 2.0 端口。它还具有两个 M.2 连接器,可用于 NVMe SSD 和 5G 模块(板上包含 Nano SIM 插槽…...
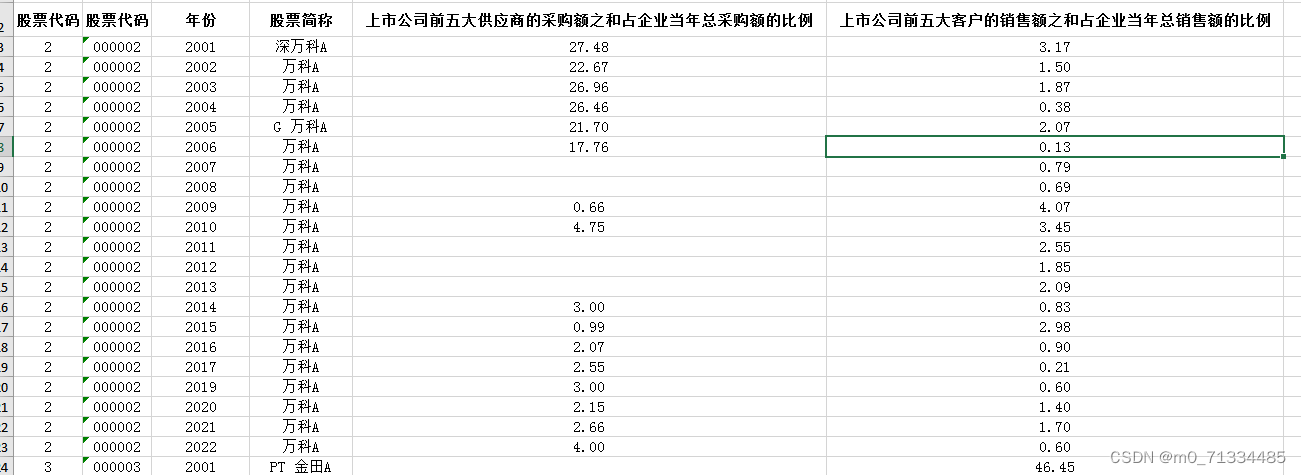
2001-2022年上市公-供应链话语权测算数据(原始数据+处理代码Stata do文档+结果)
2001-2022年上市公-供应链话语权测算数据(原始数据处理代码Stata do文档结果) 1、时间:2001-2022年 2、指标:企业代码、股票代码、年份、股票简称、上市公司前五大供应商的采购额之和占企业当年总采购额的比例、上市公司前五大客…...

如何通过ShardingJDBC进行读写分离
背景信息: 面对日益增加的系统访问量,数据库的吞吐量面临着巨大瓶颈。 对于同一时刻有大量并发读操作和较少写操作类型的应用系统来说,将数据库拆分为主库和从库。其中主库负责处理事务性的增删改操作,从库负责处理查询操作&#…...

【uniapp】部分图标点击事件无反应
比如:点击这个图标在h5都正常,在小程序上无反应 css:也设置z-index,padding 页面上也试过click.native.stop.prevent"changePassword()" 时而可以时而不行, 最后发现是手机里输入键盘的原因,输…...

MPNet:旋转机械轻量化故障诊断模型详解python代码复现
目录 一、问题背景与挑战 二、MPNet核心架构 2.1 多分支特征融合模块(MBFM) 2.2 残差注意力金字塔模块(RAPM) 2.2.1 空间金字塔注意力(SPA) 2.2.2 金字塔残差块(PRBlock) 2.3 分类器设计 三、关键技术突破 3.1 多尺度特征融合 3.2 轻量化设计策略 3.3 抗噪声…...

《Qt C++ 与 OpenCV:解锁视频播放程序设计的奥秘》
引言:探索视频播放程序设计之旅 在当今数字化时代,多媒体应用已渗透到我们生活的方方面面,从日常的视频娱乐到专业的视频监控、视频会议系统,视频播放程序作为多媒体应用的核心组成部分,扮演着至关重要的角色。无论是在个人电脑、移动设备还是智能电视等平台上,用户都期望…...

遍历 Map 类型集合的方法汇总
1 方法一 先用方法 keySet() 获取集合中的所有键。再通过 gey(key) 方法用对应键获取值 import java.util.HashMap; import java.util.Set;public class Test {public static void main(String[] args) {HashMap hashMap new HashMap();hashMap.put("语文",99);has…...

(二)原型模式
原型的功能是将一个已经存在的对象作为源目标,其余对象都是通过这个源目标创建。发挥复制的作用就是原型模式的核心思想。 一、源型模式的定义 原型模式是指第二次创建对象可以通过复制已经存在的原型对象来实现,忽略对象创建过程中的其它细节。 📌 核心特点: 避免重复初…...

linux 下常用变更-8
1、删除普通用户 查询用户初始UID和GIDls -l /home/ ###家目录中查看UID cat /etc/group ###此文件查看GID删除用户1.编辑文件 /etc/passwd 找到对应的行,YW343:x:0:0::/home/YW343:/bin/bash 2.将标红的位置修改为用户对应初始UID和GID: YW3…...

Python如何给视频添加音频和字幕
在Python中,给视频添加音频和字幕可以使用电影文件处理库MoviePy和字幕处理库Subtitles。下面将详细介绍如何使用这些库来实现视频的音频和字幕添加,包括必要的代码示例和详细解释。 环境准备 在开始之前,需要安装以下Python库:…...
)
Java入门学习详细版(一)
大家好,Java 学习是一个系统学习的过程,核心原则就是“理论 实践 坚持”,并且需循序渐进,不可过于着急,本篇文章推出的这份详细入门学习资料将带大家从零基础开始,逐步掌握 Java 的核心概念和编程技能。 …...

关键领域软件测试的突围之路:如何破解安全与效率的平衡难题
在数字化浪潮席卷全球的今天,软件系统已成为国家关键领域的核心战斗力。不同于普通商业软件,这些承载着国家安全使命的软件系统面临着前所未有的质量挑战——如何在确保绝对安全的前提下,实现高效测试与快速迭代?这一命题正考验着…...

[免费]微信小程序问卷调查系统(SpringBoot后端+Vue管理端)【论文+源码+SQL脚本】
大家好,我是java1234_小锋老师,看到一个不错的微信小程序问卷调查系统(SpringBoot后端Vue管理端)【论文源码SQL脚本】,分享下哈。 项目视频演示 【免费】微信小程序问卷调查系统(SpringBoot后端Vue管理端) Java毕业设计_哔哩哔哩_bilibili 项…...

云原生周刊:k0s 成为 CNCF 沙箱项目
开源项目推荐 HAMi HAMi(原名 k8s‑vGPU‑scheduler)是一款 CNCF Sandbox 级别的开源 K8s 中间件,通过虚拟化 GPU/NPU 等异构设备并支持内存、计算核心时间片隔离及共享调度,为容器提供统一接口,实现细粒度资源配额…...
