算法通关村-----数论问题解析
最大公约数和最小公倍数
概念描述
最大公约数(GCD)是指两个或多个整数共有约数中的最大值。
最小公倍数(LCM)是指两个或多个整数共有的倍数中的最小值
方法介绍
碾转相除法
一种用于计算两个整数的最大公约数(GCD)的方法。它基于以下原理:两个数的最大公约数等于其中较小数除以它们的余数的最大公约数。
该算法的步骤如下:
- 将两个整数记为a和b,其中a是较大的数,b是较小的数。
- 用a除以b,得到一个商q和余数r。
- 如果r等于0,则b就是最大公约数,算法结束。
- 如果r不等于0,则将a更新为b,b更新为r,然后返回第二步继续执行。
- 重复执行步骤2-4,直到余数为0为止。
两个数的乘积除以两个数的最大公约数即为两个数的最小公倍数
代码实现
求解最大公约数
public int gcd(int a, int b) {int k = 0;while (k!=0){k = a%b;a = b;b = k;};return a;
}
求解最小公倍数
public int mcl(int a, int b) {int gcd = gcd(a, b);return a * b / gcd;
}
素数与合数
概念介绍
素数又称为质数,素数首先要满足大于等于2,并且除了1和它本身之外,不能被任何其他自然数整除。其他数都是合数。比较特殊的是1即非素素数,也非合数。2是唯一的同时为偶数和素数的数字。
方法介绍
要判断一个数是否为质数,可以使用以下方法:
- 特殊情况处理:首先排除小于2的数,因为质数定义为大于1的自然数。
- 试除法:从2开始,逐个将待判断的数除以从2到其平方根范围内的所有整数(包括平方根),如果能够整除,则该数不是质数。如果在整个范围内都没有找到能整除的数,则该数是质数。
代码实现
public boolean isPrime(int num){int max = (int)Math.sqrt(num);for (int i = 2; i<=max;i++){if(num%i==0){return false;}}return true;
}
质数计数
问题描述
给定整数 n ,返回所有小于非负整数 n 的质数的数量 。详见leetcode204
问题分析
最直接的方式就是从2开始遍历,每次利用上面的质数判断代码对每一个数字进行判断,如果是质数,计数器➕1,直至计数器为n,返回当前质数。这样做时间复杂度过高。可以通过空间换时间的方式来操作,设置一个长度为n的数组,初始时,设置数组全为1,之后,从下标2开始遍历,如果数组当前值为1,质数计数器➕1,并将当前数字的倍数以及与倍数相关的非质数下标设置为0,最后返回质数计数器的值。这种方式也被称为埃氏筛
代码实现
直接方式
public int countPrimes(int n) {int count = 0;for(int i=2;i<n;i++){if(isPrime(i)){count++;}}return count;
}public boolean isPrime(int num){int max = (int)Math.sqrt(num);for (int i = 2; i<=max;i++){if(num%i==0){return false;}}return true;
}
埃氏筛方式
public int countPrimes(int n) {int[] isPrime = new int[n];int count = 0;Arrays.fill(isPrime,1);for(int i=2;i<n;i++){if(isPrime[i]==1){count++;if((long)i*i<n){for(int j=i*i;j<n;j+=i){isPrime[j]=0;}}}}return count;
}
丑数判断
问题描述
丑数 就是只包含质因数 2、3 和 5 的正整数。
给你一个整数 n ,请你判断 n 是否为 丑数 。如果是,返回 true ;否则,返回 false 。详见leetcode263
问题分析
可以直接根据丑数的概念进行判断。如果不包含质因数或者包含质因数 2、3 和 5 的正整数即为丑数
代码实现
public boolean isUgly(int n) {if(n<=0){return false;}int[] factors = new int[]{2,3,5};for(int factor:factors){while(n%factor==0){n = n/factor;}}return n==1;
}
丑数计数
问题描述
给你一个整数 n ,请你找出并返回第 n 个 丑数 。详见leetcode264
问题分析
最直接的方式就是从1开始遍历,每次利用上面的丑数判断代码对每一个数字进行判断,如果是质数,计数器➕1,直至计数器为n,返回当前丑数。这样做时间复杂度过高。可以通过空间换时间的方式来操作,设置一个小顶堆,初始时,将最小的丑数1加入队中,循环n次,每次将堆顶元素x移除,每次将2x,3x,5x放入堆中,为了避免重复,可以使用集合过滤,循环n次之后,最小的第n个丑数出堆返回
代码实现
直接方式
public int nthUglyNumber(int n) {int count = 0;int i=1;while(true){if(isUgly(i)){count++;if(count==n){return i;}}i++;}
}public boolean isUgly(int num){if(num<=0){return false;}int[] factors = new int[]{2,3,5};for(int factor:factors){while(num%factor==0){num = num/factor;}}return num==1;
}
最小堆方式
public int nthUglyNumber(int n) {int[] factors = {2, 3, 5};Set<Long> seen = new HashSet<Long>();PriorityQueue<Long> heap = new PriorityQueue<Long>();seen.add(1L);heap.offer(1L);int ugly = 0;for (int i = 0; i < n; i++) {long curr = heap.poll();ugly = (int) curr;for (int factor : factors) {long next = curr * factor;if (seen.add(next)) {heap.offer(next);}}}return ugly;
}
相关文章:

算法通关村-----数论问题解析
最大公约数和最小公倍数 概念描述 最大公约数(GCD)是指两个或多个整数共有约数中的最大值。 最小公倍数(LCM)是指两个或多个整数共有的倍数中的最小值 方法介绍 碾转相除法 一种用于计算两个整数的最大公约数(GCD…...

wpf prism当中 发布订阅 IEventAggregator
先订阅后发布 private readonly IEventAggregator _eventAggregator; public LoginViewModel(ILoginService iloginService, IEventAggregator eventAggregator) {_iloginService iloginService;_eventAggregator eventAggregator;_eventAggregator.GetEvent<MessageEven…...

Angular中的getter函数
Angular 中的 getter 函数每次被调用时会返回一个新对象时,这些新对象并不使用同一个堆内存。详细解释一下: Getter 函数的作用是获取某个属性的值。在 Angular 中,getter 函数通常用于获取响应式数据(例如 Observables 或 Signal…...
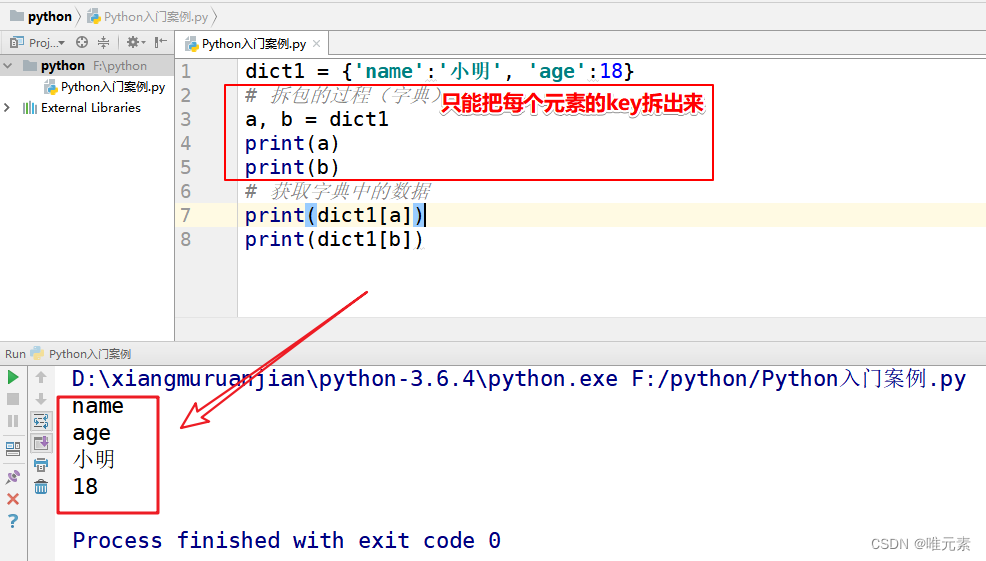
Python----函数的数据 拆包(元组和字典)
Python拆包: 就是把元组或字典中的数据单独的拆分出来,然后赋予给其他的变量。 拆包: 对于函数中的多个返回数据, 去掉 元组, 列表 或者字典 直接获取里面数据的过程。 元组的拆包过程 def func():# 经过一系列操作返回一个元组return 100, 200 …...

vim翻页快捷键
Vim翻页 整页 Ctrlf向下翻页,下一页,相当于Page DownCtrlb向上翻页,上一页,相当于Page Up 半页 Ctrld向下半页,下一半页,光标下移Ctrlu向上半页,上衣半页,光标上移 按行 Ctrle…...
死锁是什么?死锁是如何产生的?如何破除死锁?
1. 死锁是什么 多个线程同时被阻塞,它们中的一个或者全部都在等待某个资源被释放。由于线程被无限期地阻塞,因此程序不可能正常终止。 2. 死锁的三种典型情况 一个线程, 一把锁, 是不可重入锁, 该线程针对这个锁连续加锁两次, 就会出现死锁. 两个线程…...

给虚拟机配置静态id地址
1.令人头大的原因 当连接虚拟机的时候 地址不一会就改变,每次都要重新输入 2.配置虚拟机静态id地址 打开命令窗口执行 : vim /etc/sysconfig/network-scripts/ifcfg-ens33 按下面操作修改 查看自己子网掩码 3.重启网络 命令行输入 systemctl restart netwo…...
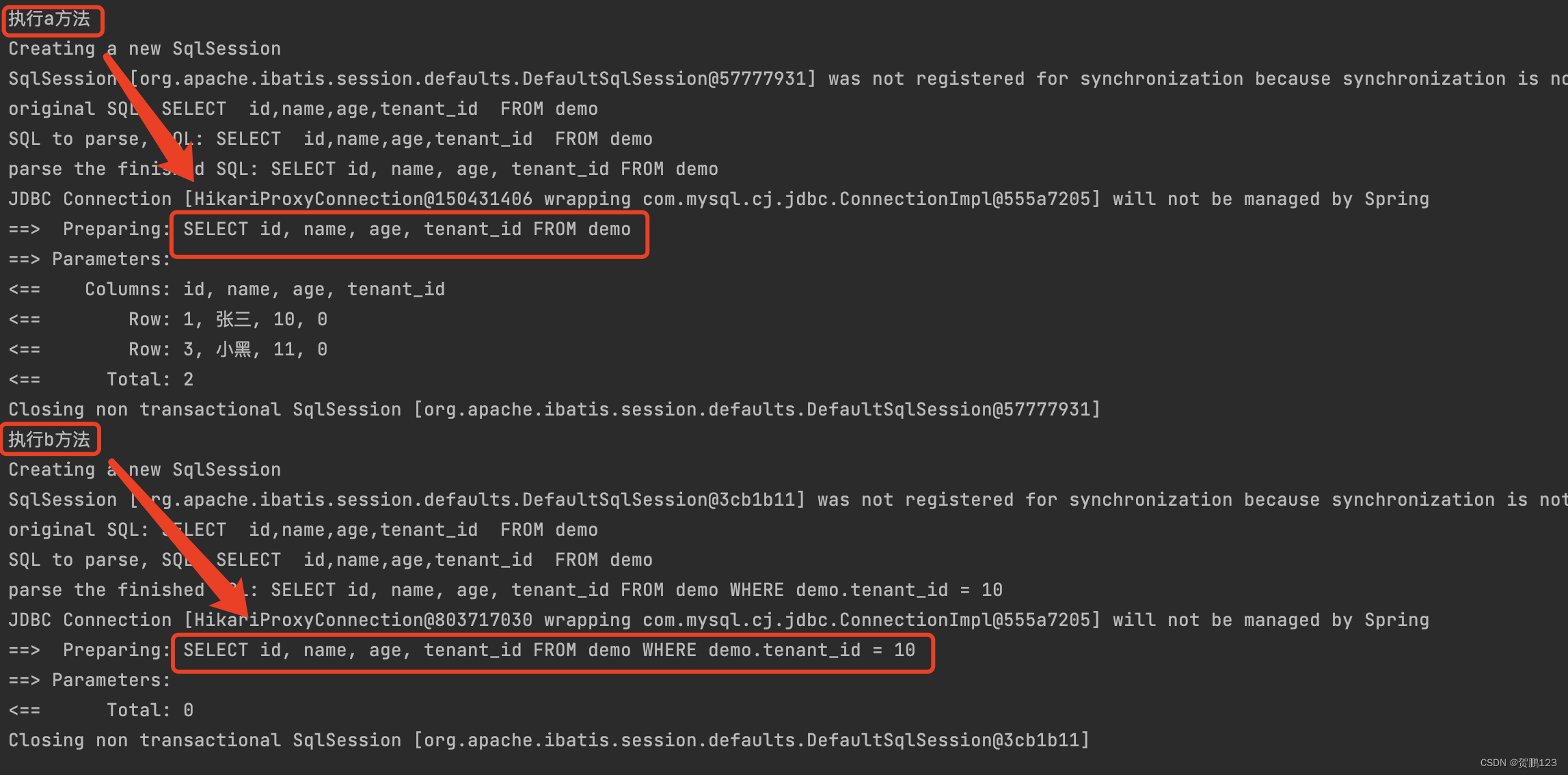
Mybatis-Plus 租户使用
Mybatis-Plus 租户使用 文章目录 Mybatis-Plus 租户使用一. 前言1.1 租户存在的意义1.2 租户框架 二. Mybatis-plus 租户2.1 租户处理器2.2 前置准备1. 依赖2. 表及数据准备3. 代码生成器 2.3 使用 三. 深入使用3.1 前言3.2 租户主体设值,取值3.3 部分表全量db操作3…...

vue el-table (固定列+滚动列)【横向滚动条】确定滚动条是在列头还是列尾
效果图: 代码实现: html: <script src"//unpkg.com/vue2/dist/vue.js"></script> <script src"//unpkg.com/element-ui2.15.14/lib/index.js"></script> <div id"app" style&quo…...

⑦【Redis GEO 】Redis常用数据类型:GEO [使用手册]
个人简介:Java领域新星创作者;阿里云技术博主、星级博主、专家博主;正在Java学习的路上摸爬滚打,记录学习的过程~ 个人主页:.29.的博客 学习社区:进去逛一逛~ Redis GEO ⑦Redis GEO 基本操作命令1.geoadd …...

LeetCode 2304. 网格中的最小路径代价:DP
【LetMeFly】2304.网格中的最小路径代价:DP 力扣题目链接:https://leetcode.cn/problems/minimum-path-cost-in-a-grid/ 给你一个下标从 0 开始的整数矩阵 grid ,矩阵大小为 m x n ,由从 0 到 m * n - 1 的不同整数组成。你可以…...

c 实用化的文本终端实时显示摄像头视频
因为采用yuv格式,帧率都很低。图像会拖影。把图像尺寸尽量缩小,能大大改善。现在最麻烦的是图像上有黑色的闪影,不知是为啥?如是framebuffer引起的就无解了。终于找到问题了,是在显示前加了一条用黑色清屏造成的&#…...

CSS中常用的伪类选择器
一 、伪类(不存在的类,特殊的类) -伪类用来描述一个元素的特殊状态 比如:第一个元素,被点击的元素,鼠标移入的元素 -特点:一般请情况下,使用:开头 1、 :first-child …...

【python学习】中级篇-数据库操作:SQLite
SQLite是一个轻量级的数据库引擎,它可以嵌入到各种应用程序中。以下是SQLite的基本用法: 创建数据库文件 import sqlite3# 连接到一个不存在的数据库文件,如果文件不存在,将会自动创建一个新的数据库文件 conn sqlite3.connect…...

汇编-PROTO声明过程
64位汇编 64 模式中,PROTO 伪指令指定程序的外部过程,示例如下: ExitProcess PROTO ;指定外部过程,不需要参数.code main PROCmov ebx, 0FFFFFFFFh mov ecx,0 ;结束程序call ExitProcess ;调用外部过程main ENDP END 32位…...

MYSQL事务操作
...
自动化测试——自动卸载软件
📢专注于分享软件测试干货内容,欢迎点赞 👍 收藏 ⭐留言 📝 如有错误敬请指正!📢交流讨论:欢迎加入我们一起学习!📢资源分享:耗时200小时精选的「软件测试」资…...
)
Linux - 系统调用(syscall)
说明 基于riscv64 soc linux_5.10.4平台,通过新增一个系统调用深入了解下系统调用实现原理。 简介 Linux 软件运行环境分为用户空间和内核空间,默认情况下,用户进程无法访问内核,既不能访问内核所在的内存空间,也不…...

c语言-冒泡排序
冒泡排序原理: 冒泡排序是一种简单直观的排序算法,它重复地遍历待排序的元素序列,比较相邻的两个元素,如果它们的顺序不符合要求(例如升序要求前面的元素小于后面的元素),则交换它们的位置。遍历…...

Mysql面经
Select语句的执行顺序 1、from 子句组装来自不同数据源的数据; 2、where 子句基于指定的条件对记录行进行筛选; 3、group by 子句将数据划分为多个分组; 4、使用聚集函数进行计算;AVG() SUM() MAX() MIN() COUNT() 5、使用 havin…...

Chapter03-Authentication vulnerabilities
文章目录 1. 身份验证简介1.1 What is authentication1.2 difference between authentication and authorization1.3 身份验证机制失效的原因1.4 身份验证机制失效的影响 2. 基于登录功能的漏洞2.1 密码爆破2.2 用户名枚举2.3 有缺陷的暴力破解防护2.3.1 如果用户登录尝试失败次…...

[2025CVPR]DeepVideo-R1:基于难度感知回归GRPO的视频强化微调框架详解
突破视频大语言模型推理瓶颈,在多个视频基准上实现SOTA性能 一、核心问题与创新亮点 1.1 GRPO在视频任务中的两大挑战 安全措施依赖问题 GRPO使用min和clip函数限制策略更新幅度,导致: 梯度抑制:当新旧策略差异过大时梯度消失收敛困难:策略无法充分优化# 传统GRPO的梯…...

盘古信息PCB行业解决方案:以全域场景重构,激活智造新未来
一、破局:PCB行业的时代之问 在数字经济蓬勃发展的浪潮中,PCB(印制电路板)作为 “电子产品之母”,其重要性愈发凸显。随着 5G、人工智能等新兴技术的加速渗透,PCB行业面临着前所未有的挑战与机遇。产品迭代…...

遍历 Map 类型集合的方法汇总
1 方法一 先用方法 keySet() 获取集合中的所有键。再通过 gey(key) 方法用对应键获取值 import java.util.HashMap; import java.util.Set;public class Test {public static void main(String[] args) {HashMap hashMap new HashMap();hashMap.put("语文",99);has…...

【HarmonyOS 5.0】DevEco Testing:鸿蒙应用质量保障的终极武器
——全方位测试解决方案与代码实战 一、工具定位与核心能力 DevEco Testing是HarmonyOS官方推出的一体化测试平台,覆盖应用全生命周期测试需求,主要提供五大核心能力: 测试类型检测目标关键指标功能体验基…...

抖音增长新引擎:品融电商,一站式全案代运营领跑者
抖音增长新引擎:品融电商,一站式全案代运营领跑者 在抖音这个日活超7亿的流量汪洋中,品牌如何破浪前行?自建团队成本高、效果难控;碎片化运营又难成合力——这正是许多企业面临的增长困局。品融电商以「抖音全案代运营…...

VTK如何让部分单位不可见
最近遇到一个需求,需要让一个vtkDataSet中的部分单元不可见,查阅了一些资料大概有以下几种方式 1.通过颜色映射表来进行,是最正规的做法 vtkNew<vtkLookupTable> lut; //值为0不显示,主要是最后一个参数,透明度…...

【Oracle】分区表
个人主页:Guiat 归属专栏:Oracle 文章目录 1. 分区表基础概述1.1 分区表的概念与优势1.2 分区类型概览1.3 分区表的工作原理 2. 范围分区 (RANGE Partitioning)2.1 基础范围分区2.1.1 按日期范围分区2.1.2 按数值范围分区 2.2 间隔分区 (INTERVAL Partit…...
混合(Blending))
C++.OpenGL (20/64)混合(Blending)
混合(Blending) 透明效果核心原理 #mermaid-svg-SWG0UzVfJms7Sm3e {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-icon{fill:#552222;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-text{fill…...

push [特殊字符] present
push 🆚 present 前言present和dismiss特点代码演示 push和pop特点代码演示 前言 在 iOS 开发中,push 和 present 是两种不同的视图控制器切换方式,它们有着显著的区别。 present和dismiss 特点 在当前控制器上方新建视图层级需要手动调用…...
